Branko Mišković
Retired Researcher
Correspondence to: Branko Mišković, Retired Researcher.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Diversified empirical development of EM theory overlooked some theoretical aspects or details of this complex physical discipline. After its additional inductive elaboration, the reverse deductive exposition of thus advanced theory would enable the revelation and correction of its remaining lacks. Starting from founded supposition of a compressible, super-fluidic and inert medium, as the sufficient starting view, EM theory is here exposed deductively. The three mentioned fluid features enable static, kinetic and dynamic phenomena, respectively. All the quantities and their relations are convincingly interpreted aerodynamically. With respect to the wider – 4D context, the known 3D analogies are generalized. In addition, the media stratification along structural depths points to an additional dimension, as the fifth.
Keywords:
EM Theory, Deductive Exposition, Fluid Mechanics, Quantum Fluid
Cite this paper: Branko Mišković, Deductive Exposition of EM Theory, International Journal of Electromagnetics and Applications, Vol. 3 No. 2, 2013, pp. 20-26. doi: 10.5923/j.ijea.20130302.03.
1. Introduction
Inductive elaboration of a theory consists in gradual generalization of established empirical facts. Each such step forward into unknown is hypothetical in some extent, with the real risk from excessive or erroneous generalizations. Inevitable mathematical improvisations complicate the exposition, thus diminishing the consistency of inductive theories. Their lacks are tried to notice and correct by further experimental testing and practical application.A theory reducible to a few basic laws can be exposed deductively. The transparency of its procedures and conclusions simplifies the exposition, with minimizing of procedural errors. However, the majority of scientific responsibility then falls to the adopted axioms. Less founded starting views, via difficulties in the exposition, follow into contradictory or unacceptable results. A theory reducible to another one would lose the basic status of its laws.As the example and our subject, there is EM theory, with its differential equations. Although being the spine of the theory, these equations are non-transparent implicit relations of a vague sense and unconvincing introduction. However, concerning the static potential, as the pressure disturbance of a hypothetical – compressible, super-fluidic and inert – medium, the basic equations can be introduced as the definitions of EM quantities, starting by this potential.
2. Constitutive Relations
EM theory is founded dually, on the two EM fields. Though the two electric components are formally distinct, static as non-vortical, and dynamic as vortical, Maxwell’s equations at least implicitly concern their sum: 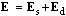 . These two fields are collinear with respective forces, unlike magnetic one, perpendicular to the kinetic (magnetic) forces. The dual treatment understands the two pairs of Maxwell’s equations, determining the two fields. However, one of these equations is trivial and practically excessive.Some stratification of the media – by volume derivation
. These two fields are collinear with respective forces, unlike magnetic one, perpendicular to the kinetic (magnetic) forces. The dual treatment understands the two pairs of Maxwell’s equations, determining the two fields. However, one of these equations is trivial and practically excessive.Some stratification of the media – by volume derivation 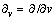 , may be taken for a structural dimension, as the fifth. The domain of observation on this axis is limited from bottom by the value
, may be taken for a structural dimension, as the fifth. The domain of observation on this axis is limited from bottom by the value 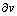 , as the minimal relevant volume. Logarithm of radii of this zooming volume gives two unrestricted legs of the new axis, one of them striving into cosmic widths, and the other – into structural depths. The axis zero is determined by a convenient unit of length. Though distinct from the spatial and temporal axes, this one is formally equal with them. It is more convincing than the widely accepted one, closed into itself on the level of elementary particles, without palpable physical interpretation. With respect to our new axis, apart from the three spatial, and fourth – temporal terms, a 5D continuity equation demands a substantial term, as the fifth, describing structural transformation of the observed substance.EM processes take part in four structural layers: vacuum, dielectric, magnetic and conducting ones. First of them concerns free space or vacuum fields: electric (E) and magnetic (H). The two next layers are substrata of the material field components: polarization (P) and magnetization (M). Respective sums give the two total fields:
, as the minimal relevant volume. Logarithm of radii of this zooming volume gives two unrestricted legs of the new axis, one of them striving into cosmic widths, and the other – into structural depths. The axis zero is determined by a convenient unit of length. Though distinct from the spatial and temporal axes, this one is formally equal with them. It is more convincing than the widely accepted one, closed into itself on the level of elementary particles, without palpable physical interpretation. With respect to our new axis, apart from the three spatial, and fourth – temporal terms, a 5D continuity equation demands a substantial term, as the fifth, describing structural transformation of the observed substance.EM processes take part in four structural layers: vacuum, dielectric, magnetic and conducting ones. First of them concerns free space or vacuum fields: electric (E) and magnetic (H). The two next layers are substrata of the material field components: polarization (P) and magnetization (M). Respective sums give the two total fields: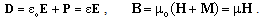 | (1) |
The total fields and their vacuum components are mutually related: electric – by static 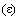 , and magnetic ones – by dynamic
, and magnetic ones – by dynamic 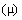 constants. Apart from the medial features, these constants determine the quantities and units. Their two roles are separated by the factorization:
constants. Apart from the medial features, these constants determine the quantities and units. Their two roles are separated by the factorization: 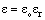 ,
, 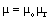 . The vacuum factors harmonize quantities and units, and relative ones express the features of material media.The force fields (E & B) are introduced as the specific actions on respective unit objects, and rational ones (D & H), – as vector densities of respective elementary dipoles. Their asymmetric positions in (1) point to the distinct structural levels of the two EM forces. As if electric forces act at vacuum only, but magnetic ones concern the material layer too. The dimensional equalling of respective fields, by the unit vacuum factors – expressed in natural units, turns these two equations into more symmetric forms.
. The vacuum factors harmonize quantities and units, and relative ones express the features of material media.The force fields (E & B) are introduced as the specific actions on respective unit objects, and rational ones (D & H), – as vector densities of respective elementary dipoles. Their asymmetric positions in (1) point to the distinct structural levels of the two EM forces. As if electric forces act at vacuum only, but magnetic ones concern the material layer too. The dimensional equalling of respective fields, by the unit vacuum factors – expressed in natural units, turns these two equations into more symmetric forms.
3. Static Relations
Let a subtle fluid be taken as the substantial essence of 4D space, including the particles, as its disturbances. Say that this medium is denser around positive, and sparser around negative particles. Tending to the fluid homogeneity, two equipolar particles repel, and opposite ones attract each other. The first and last fluid features, as elasticity and mass density , are the bases of the static and dynamic effects, dependent on a distance or acceleration, respectively, of the disturbances. As such, these two fluid features determine the speed of EM wave propagation: 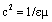 . Internal pressure of the compressible fluid equals to the energy density, and each its disturbance, as the elementary static potential, provides the energy for all other such disturbances, as the objects. This quantity determines the static field, and this field itself – carrying charge:
. Internal pressure of the compressible fluid equals to the energy density, and each its disturbance, as the elementary static potential, provides the energy for all other such disturbances, as the objects. This quantity determines the static field, and this field itself – carrying charge: | (2) |
Each new quantity in this sequence is the formal feature of the preceding one. The static field is the gradient of respective potential. The beginnings of the field lines represent the positive, and their terminals – negative charges. Static field thus mediates the relation of electric charge and respective potential. Thus introduced, the static quantities are the bases for following definition of kinetic ones.
4. Kinetic Relations
The medium super-fluidity enables continual fluid flows. In parallel to the current field definition (3b), the motion of a static, as the pressure disturbance, forms the kinetic potential, as the linear momentum density (3a): | (3) |
The product of compressibility 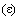 , regular density and pressure disturbance
, regular density and pressure disturbance 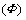 gives the density disturbance
gives the density disturbance 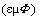 . The charges are inseparable from their potentials, and so the two kinetic quantities are collinear. At motion of negative static quantities, these two are opposite. The equation (3a) defines the kinetic potential by motion of static one. Let us now examine their mutual differential relation. Namely, div-operator applied directly to (3a) gives so called Lorentz’ condition, as the continuity equation differentially relating the two EM potentials:
. The charges are inseparable from their potentials, and so the two kinetic quantities are collinear. At motion of negative static quantities, these two are opposite. The equation (3a) defines the kinetic potential by motion of static one. Let us now examine their mutual differential relation. Namely, div-operator applied directly to (3a) gives so called Lorentz’ condition, as the continuity equation differentially relating the two EM potentials: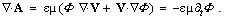 | (4) |
Dilatation and convection of a static, determine the kinetic potential. Moving together with its carrying charge, the static potential behaves as a rigid structure, of homogeneous speed. The former term thus annuls, with the convective derivative, 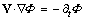 , – in the latter term. This derivative is opposite to the gradient of the moving potential.There is well-known that parallel fluid flows attract, and opposite ones repel each other – by transverse kinetic forces. Magnetic field, representing these forces, is thus defined as the curl of the kinetic potential (5a). In the similar manner, its own curl will soon be identified as the current field, in all the three electric structural layers (5b):
, – in the latter term. This derivative is opposite to the gradient of the moving potential.There is well-known that parallel fluid flows attract, and opposite ones repel each other – by transverse kinetic forces. Magnetic field, representing these forces, is thus defined as the curl of the kinetic potential (5a). In the similar manner, its own curl will soon be identified as the current field, in all the three electric structural layers (5b): | (5) |
Here 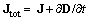 is the total current field consisting of the convection and conduction components – in the former, and displacement one – in the latter terms, at vacuum, conductors and dielectrics, respectively. The magnetic field is transverse to the other two (collinear) vectors. In accord to the relations (3) of the two potentials or carriers, their intermediate quantities can be similarly related. The substitution of (3a) into (5a) gives:
is the total current field consisting of the convection and conduction components – in the former, and displacement one – in the latter terms, at vacuum, conductors and dielectrics, respectively. The magnetic field is transverse to the other two (collinear) vectors. In accord to the relations (3) of the two potentials or carriers, their intermediate quantities can be similarly related. The substitution of (3a) into (5a) gives: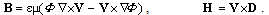 | (6) |
With respect to motion of the rigid elementary static potentials, the former term in (6a) annuls, and (2a) substituted into the latter term gives the convective kinetic relation (6b). A moving electric, produces magnetic field, representing the transverse kinetic forces. Curl applied to (6b), excluding the spatial derivatives of the speed, gives (5b):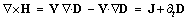 | (5b) |
An object charge moving axially, along the current and its potential, is affected by some kinetic induction, expressible by the equivalent electric quantities: | (7) |
These equations are formally inverse to the definitions (3), with the product 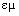 – consequently replaced. The negative signs point to the attractive (or repulsive) interactions. Grad applied to (7a), after missing of the spatial derivatives of the object speed, gives respective field:
– consequently replaced. The negative signs point to the attractive (or repulsive) interactions. Grad applied to (7a), after missing of the spatial derivatives of the object speed, gives respective field: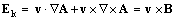 | (8) |
Dot product in (7a) restricts the motion to the longitudinal direction. Therefore, the former middle term in (8) annuls. In the similar way, div applied to (8) gives (7b), as the kinetic interaction of the two parallel currents.
5. Dynamic Relations
With respect to the known force action law and supposed inertia of the massive omnipresent quantum fluid, time derivative of the kinetic potential, representing the linear momentum density (3a), gives the reactive dynamic forces, as respective electric field component: | (9) |
Curl applied to (9a), with respect to (5a), gives the dynamic equation (9b). Similarly, div applied to (5a), via mixed vector product, gives the trivial Maxwell’s equation: 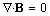 . It only speaks against the existence of any free magnetic poles, being possibly predicted in advance.The kinetic potential and magnetic field are the two perpendicular vortical fields, and their gradient, perpendicular to the common surface, is a non-vortical field. The motion in this direction varies the potential on the object, and – with respect to (9a), induces some dynamic field:
. It only speaks against the existence of any free magnetic poles, being possibly predicted in advance.The kinetic potential and magnetic field are the two perpendicular vortical fields, and their gradient, perpendicular to the common surface, is a non-vortical field. The motion in this direction varies the potential on the object, and – with respect to (9a), induces some dynamic field: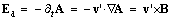 | (10) |
Here 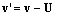 is transverse mutual (charge-field) speed. In the observed direction:
is transverse mutual (charge-field) speed. In the observed direction: 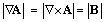 . Really, in the opposite sense, curl applied to (10) gives (9b):
. Really, in the opposite sense, curl applied to (10) gives (9b):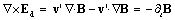 | (9b) |
As before, all the speed derivatives are missed. Transverse mutual (charge-field) motion induces some dynamic forces, represented by respective electric field. On the other hand, an object charge, moving in direction of the causing current (7), suffers the transverse kinetic force (8). However, with respect to (10), a current carrying conductor, moving in the same direction (of the zero gradient), would not cause any inductive effect. This direction does not obey the principle of relativity. Unlike (7b), as the apparent charge, the real charge cannot be obtained by axial motion of a current, at least in the frames of 3D space.Without respect to the charge motion, (10) is reduced to the convective dynamic relation: 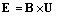 . Together with the kinetic one (6b), it forms the convective pair of J. J. Thomson. With respect to above procedures, neglecting all spatial derivatives of the field speeds, this pair is restricted to the uniform rectilinear motion. With the additional restriction of the speed direction in (10), these two relations seemed to be very problematic. The restrictions were the reasons of their missing from the standard EM theory.
. Together with the kinetic one (6b), it forms the convective pair of J. J. Thomson. With respect to above procedures, neglecting all spatial derivatives of the field speeds, this pair is restricted to the uniform rectilinear motion. With the additional restriction of the speed direction in (10), these two relations seemed to be very problematic. The restrictions were the reasons of their missing from the standard EM theory.
6. Field Tensor
The static and kinetic equations (2,5-b) in the componential form represent the set of the four partial differential equations. With the general ordinal indexation, this pair is turned into the following tensor equation: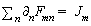 | (11a) |
Here 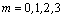 is the ordinal number of equation, with the summation performed per the index
is the ordinal number of equation, with the summation performed per the index 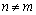 . The charge carried by cosmic expansion along t-axis forms respective current component (J0). All the separate field components (Fmn) are identified by the following tensor:
. The charge carried by cosmic expansion along t-axis forms respective current component (J0). All the separate field components (Fmn) are identified by the following tensor: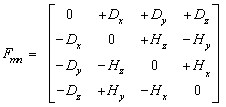 | (11b) |
This tensor affirms 4D space, as the ambient of EM quantities. The six term pairs accord to the six planes of 4D space, as the field locations. The first row and column concern the three ‘longitudinal’ planes (tx, ty, tz), with electric field. The remaining sub-tensor accords to the three ‘transverse’ planes (xy, yz, zx), containing magnetic field. The planes are classified with respect to probable motion of all the matter, directed along temporal axis, and projected into 3D space as the known cosmic expansion. EM potentials, as the two initial quantities, belong to the four axes: static to t, and kinetic to x, y & z-axes. The two carriers, as the final EM quantities, belong to respective 3D subspaces: electricity to xyz, and current – to xyt, xtz & tyz ones.
7. Field Unification
With respect to Lorentz’ condition (4), the application of (2b) to the sum of (2,9-a) relates the two electric quantities, charge and respective static potential (12a): | (12) |
In accord to (3), (12a) multiplied by the product 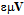 gives (12b). The same result can be obtained from (5). The two temporal terms accord to the dynamic, and spatial ones – to static fields. With respect to above procedure, the equations (2,5-b) understand both – static and dynamic field components, speaking thus in favour of their unity. To confirm this, let us compose the 4D potential, as the fluid flows of the two orthogonal components, from the temporal and spatial domains:
gives (12b). The same result can be obtained from (5). The two temporal terms accord to the dynamic, and spatial ones – to static fields. With respect to above procedure, the equations (2,5-b) understand both – static and dynamic field components, speaking thus in favour of their unity. To confirm this, let us compose the 4D potential, as the fluid flows of the two orthogonal components, from the temporal and spatial domains: 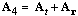 . With respect to the electric field components (2,9-a), their sum gives the following united mathematical form:
. With respect to the electric field components (2,9-a), their sum gives the following united mathematical form: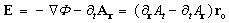 | (13) |
The dimensional distinction of the two axes (r & t) is here neglected, as in natural units. Positive fluid flows, directed into t-axis course, superimposed to the cosmic expansion – with respect to Bernoulli’s law – produce the negative static potentials, and opposite. Time derivative of Ar represents its gradient directed into the future.A hyper-toroidal vortex of the vacuum fluid, coaxial with temporal axis, accords to the circular magnetic vortexes – in 3D. In analogy to (7b), axial motion of such a vortex forms the real electric charge. Therefore, such a composition may be taken as the particle model. The internal fluid flow, directed along t-axis, is just continued by the opposite external one. With respect to (13), the external flow is manifest in 3D as respective potential, positive or negative.
8. EM Energy
EM energy densities at disturbed media express the object displacements in respective external fields: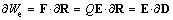 | (14a) |
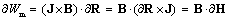 | (14b) |
The two objects (electricity and its current) are displaced in electric or magnetic fields, respectively. The referent zeroes accord to the undisturbed media. The integration of the two external equalities finally gives: | (15) |
In the pairs of the collinear similar fields, the dot products turn into ordinary ones. At the complex material media, these energy densities are distributed amongst the vacuum and respective material structural layers: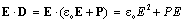 | (16a) |
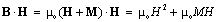 | (16b) |
In the natural units, these two expressions are symmetric. SI vacuum constants disturb this symmetry. Moving fields are inevitably followed by their own energies. In this sense, dot multiplication of (5b) by the field E, and of (9b) – by H, with subtraction of the former from the latter result, gives a typical 5D continuity equation, with the spatial, temporal and substantial terms: 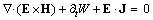 | (17) |
It is known as Poynting’s theorem. The temporal term expresses the energy density variation, and substantial one – the power of energy dissipation: 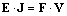 . This dissipation may be understood as energy dislocation along the fifth axis, from one into another structural layers.The cross product of the two fields, in the spatial term, represents the current field of EM energy:
. This dissipation may be understood as energy dislocation along the fifth axis, from one into another structural layers.The cross product of the two fields, in the spatial term, represents the current field of EM energy: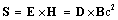 | (18) |
In accord to Einstein’s equation (35a), the product of the total fields represents equivalent linear momentum density. This relation of the two currents, expressed by the fields, reminds of (3a), relating the two potentials.
9. Moving Fields
Instead of the field variation – in Maxwell’s equations, the algebraic relations treat their motion. Moving electric, produces magnetic field (6b), affecting kinetically the charges moving in parallel – by respective field (8):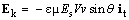 | (19) |
Here θ is the polar angle between the direction of motion and the moving field itself. The obtained kinetic field just depends on the speed product. Possible transverse component of the object speed, directed along the field gradient, would produce the axial dynamic induction.With respect to (9a,4,2a), axial convective variation of the kinetic potential causes some dynamic field: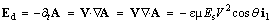 | (20) |
The longitudinal gradient equals to the divergence. Thus obtained electric field, independent of the object speed, is directed axially, towards the carrier. It points to some acceleration of the medium in the front, and its deceleration behind moving charge. Subtracted from the moving static field, it causes the ellipsoidal field deformation. SRT ascribed this effect to the increased transverse fields.The vector sum of the two field components – kinetic (19) and dynamic (20) – affects all the present electric charges, including the causing charge itself: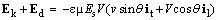 | (21) |
In the resting frame (v = 0), this is reduced to the latter term. In the moving frame (V = v), vector sum of the two components represents the central field. Its subtraction from the moving static field as if scales this field: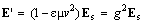 | (22) |
The transverse field component, acting on moving charges, is scaled by the factor: 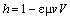 . With some formal inconsistencies and fantastic interpretations, the two factors play the crucial roles in foundation of SRT.Moving EM fields carry by themselves respective energies. The two convective fields,
. With some formal inconsistencies and fantastic interpretations, the two factors play the crucial roles in foundation of SRT.Moving EM fields carry by themselves respective energies. The two convective fields, 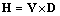 &
& 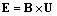 , substituted into Poynting’s relation (18), express the two energetic currents, electric and magnetic ones:
, substituted into Poynting’s relation (18), express the two energetic currents, electric and magnetic ones: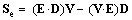 | (23a) |
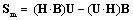 | (23b) |
The latter current components flow along the moving fields: the carriers accept the energies in front, and release behind themselves, without variation of the moving energies. The former terms, however, represent the main streams, moving at the field speeds. They understand the double energy densities, obtained by (15). The energetic densities are invariant of the field speeds, and so the moving energies are increased by extension of the spatial domain only.
10. EM Waves
Unlike some views of only longitudinal fluid undulation, the super-fluidity and transverse kinetic forces maintain the transverse oscillation of the medium. The direction is oriented in relation to the kinetic potential. The longitudinal waves of electric current in line conductors are followed by the transverse waves of surrounding fields. The two mutually related waves are thus inseparable, with cyclic alternation and mutual support of the three fields. At dielectric media, without free electricity and respective current, the pair (12) is reduced to the wave equations, with the known final solution: 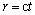 . The radius (r) concerns the wave cross-section in the plain of propagation. With respect to Poynting’s relation (18), the speed of EM wave propagation is determined by the ratio of the energetic and equivalent mass currents, as the two collinear flows, being perpendicular to both EM fields:
. The radius (r) concerns the wave cross-section in the plain of propagation. With respect to Poynting’s relation (18), the speed of EM wave propagation is determined by the ratio of the energetic and equivalent mass currents, as the two collinear flows, being perpendicular to both EM fields: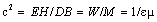 | (24) |
This speed represents the ratio of the products of the vacuum and total fields. Compared in the natural units, this mass is greater or equal to the energy. This is finally expressed by the two constants, as the medial features.In accord to the causal loop (closed into itself) of the processes of EM wave propagation, magnetic field eliminated from the two convective relations gives: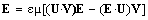 | (25) |
At least in the transverse waves, the latter term annuls, reducing the equality to the following identity: | (26) |
The last result points to the two separate, possibly different speeds of the two fields, with the general speed of the wave propagation, as their geometric average.In the case of the transverse waves and respective fields, the latter terms in (23) annul, and two former ones represent the same current of EM wave energy: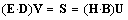 | (27) |
With respect to – expectably equal – vacuum components (28a), this directly gives (28b), additionally relating the two field speeds. By help of their above product (26b), the two speeds can be finally determined (29): | (28) |
 | (29) |
Substituted into (26b) they give the known refraction factor, 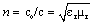 , as the ratio of the speeds of wave propagation through vacuum and matter.On the other hand, the arithmetic average of the two sides of (27) explicates the wave propagation:
, as the ratio of the speeds of wave propagation through vacuum and matter.On the other hand, the arithmetic average of the two sides of (27) explicates the wave propagation: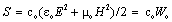 | (30) |
Vacuum layer only transfers the wave energy, at the speed co. The material layers temporarily absorb respective fractions of the energy, thus increasing its density, and decreasing the propagation. The separate speeds of the two EM fields are, in fact, the two effective physical quantities. As the analogy to the particle, with the known similarities and distinctions, a toroidal vortex of displacement current, with the circular magnetic field, may be predicted as the photon model. It is some combination of the longitudinal and transverse waves. This model is superior to the impossible wave packet. Unlike particles, transferred from the temporal into spatial domains, and thus strictly quantized, the photon energy, 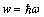 – from 3D, obtains continual values. On the other hand, with respect to the vacuum fluid and particles, constituting the expanding matter, light propagation is related to this matter, as the moving medium.
– from 3D, obtains continual values. On the other hand, with respect to the vacuum fluid and particles, constituting the expanding matter, light propagation is related to this matter, as the moving medium.
11. Moving Media
Instead of the carriers and objects, let us consider causal processes around a third medial body moving through the external fields. These fields statically induce the material fields, polarization and/or magnetization: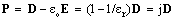 | (31a) |
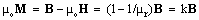 | (31b) |
The results are proportional to the fractional factors j or k. The asymmetry of SI relations conceals these factors. The symmetry is full in the natural units 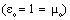 . Fresnel’s incorrect factor,
. Fresnel’s incorrect factor, 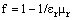 , is reduced into one of these two, at exclusively dielectric or magnetic media.The material fields are continued by similar associated fields, in the surroundings. Moving together with the medial body, these fields produce dissimilar convective inductions, superimposed to the given fields:
, is reduced into one of these two, at exclusively dielectric or magnetic media.The material fields are continued by similar associated fields, in the surroundings. Moving together with the medial body, these fields produce dissimilar convective inductions, superimposed to the given fields: | (32) |
Here u is the medial body speed. These two transformations thus express the final results in the space. Carrying the accumulated wave energies, moving media also influence the wave propagation: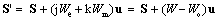 | (33) |
Here S is energetic current through resting, and S' – through moving medium. The two factors substituted into the former, give the latter expression. The body carries the accumulated energies. Some transverse speed component would distort the direction of the wave propagation.
12. Moving Charge
With respect to (2b), an electric charge (q1) affects another (q2) by the static force, expressed by the known Coulomb’s law (34a). On the other hand, its central static field, moving at the speed V, produces the summary field (21). In the case of nearly equal speeds of the carrier and its object 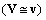 , the kinetic central forces, opposite to the static ones, may be expressed by the symmetric equation (34b):
, the kinetic central forces, opposite to the static ones, may be expressed by the symmetric equation (34b):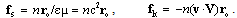 | (34) |
The substitutive factor 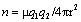 simplifies the equations. Its integration along the radii gives the factor
simplifies the equations. Its integration along the radii gives the factor 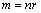 , turning thus the forces into energies:
, turning thus the forces into energies:  | (35) |
Einstein’s equation (35a), as the alternation of the law (34a), determines the energy of a resting (or any) charge. However, the integration of the static energy (15a) around a charged particle gives only a half of this value. This result points to the other its half, un-manifest in the external electric field, but belonging to the internal fluid flow.Variation in time of the kinetic energy (35b) accords to the acceleration or deceleration of the carrier. In this sense, time derivative of this equation, partially – per mV, gives the power of dynamic transfer of energy: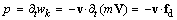 | (36) |
The last equality is nothing else than force action law, in the function of the mutual or proper masses: | (37) |
The two masses represent the elementary factors of induction and self-induction, respectively. The particle radius (ro) is the distance of the surface charge from its own centre. Therefore, a lesser particle accords to the greater mass and energy, or opposite. In fact, a half of this mass is located in the external electric field. A complex – globally neutral – body, as the multi-pole, manifests a little defected sum of the masses of its constituent particles. With this clear result, the supposition of any mass boson is excessive.A sole moving charge, as the object of its own fields, is affected by the difference of the static and kinetic forces (34) distributed about the spherical surface: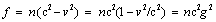 | (38) |
The factor n depends on the radius, and g – on the speed. Tending to zero – approaching the speed c, from noc2, where 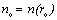 – at rest, this force strives to expand the particle. Therefore, at all the speeds, it must be opposed by a constant external pressure (fo), determined at rest. The balance (f = fo) gives the following two equalities:
– at rest, this force strives to expand the particle. Therefore, at all the speeds, it must be opposed by a constant external pressure (fo), determined at rest. The balance (f = fo) gives the following two equalities: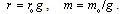 | (39) |
The latter equation represents well-known Lorentz’ mass function, dependent on speed. This function was the basis for indirect derivation of Einstein’s equation (35a). It is here explicitly interpreted, irrespective of SRT.The dynamic forces, from the force action law (36), may be resolved by derivation of the linear momentum expressed in the form of the three following factors: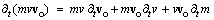 | (40) |
Here v is the speed modulus, and vo – unit vector. With the mass derivative per speed, 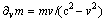 , this gives the two forces, centrifugal and inertial ones:
, this gives the two forces, centrifugal and inertial ones: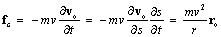 | (41a) |
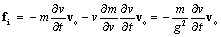 | (41b) |
Here 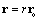 is the path curvature radius. Both forces are additionally scaled – due to the variable mass. Instead of the two different masses, the two forces are in fact the distinct functions of the same variable mass. The former force strives only to the strait direction of the motion, but the latter one changes the energy of a moving body. A moving charge is considered as the invariant quantity. However, if the definition (2b), apart from the static – concerns the dynamic field (20), with the invariant transverse components, there is the charge function:
is the path curvature radius. Both forces are additionally scaled – due to the variable mass. Instead of the two different masses, the two forces are in fact the distinct functions of the same variable mass. The former force strives only to the strait direction of the motion, but the latter one changes the energy of a moving body. A moving charge is considered as the invariant quantity. However, if the definition (2b), apart from the static – concerns the dynamic field (20), with the invariant transverse components, there is the charge function: 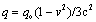 . At the upper boundary speed of the particle motion (v = c), it would be reduced in the ratio 2/3. Just this value is known from the quark theory. Instead of its dividing, the charge is here diminished. From transverse directions, however, the charge seems to be the invariant quantity.
. At the upper boundary speed of the particle motion (v = c), it would be reduced in the ratio 2/3. Just this value is known from the quark theory. Instead of its dividing, the charge is here diminished. From transverse directions, however, the charge seems to be the invariant quantity.
13. Orientation in Space
The above EM interactions depend on the three kinematical states: position, motion and acceleration. All of them usually depend on mutual distances of interacting charges. Moreover, the forces (19) & (20) also depend on the carrier and/or object speeds. Apart from the speed – via the variable mass, the two forces (41) also depend on acceleration. There arises the question of a valid frame of reference for all the three kinematical quantities. At least implicitly, some local frames, connected to predominant masses of nearby celestial bodies, are usually used in the practice. For instance, the paths of satellites are referred to respective planets, and of planets themselves – to respective stars.With respect to the dynamic induction (10), dependent on the motion along the field gradient, the principle of relativity is usually understood, irrespective of the referent frame used. However, the direction of the carrying current, with the zero field gradient, has not been taken into account. Moreover, with respect to (41), dependent on acceleration, the frame equivalence is restricted to so called inertial (un-accelerated) frames. For similar reasons, the functions of speed should be restricted to unmoving frames, and that of position – to only one, somehow preferred, frame. Despite, inertial frames are the deductive basis for foundation of SRT.The procedure observes a common detector moving at a uniform speed v through resting EM fields, thus indicating the relative EM inductions. Their addition to the given fields gives the classical field transformations: | (43) |
This is their direct set. Let us invert this set – per the primed fields, by means of determinant theory: | (44) |
The set determinant, 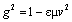 , accidentally equal to the factor contained in the function (38), points to essential inequality of the two frames, speaking thus in favour of the privileged status of some local frame.For the sake of the frame equivalence, SRT distributed this factor, by g–1 in each of the sets. This scaling of the transverse field components calls in question Maxwell’s equations, as the most general field distributions. In the aim to preserve their form, the longitudinal and temporal axes are artificially complementarily transformed:
, accidentally equal to the factor contained in the function (38), points to essential inequality of the two frames, speaking thus in favour of the privileged status of some local frame.For the sake of the frame equivalence, SRT distributed this factor, by g–1 in each of the sets. This scaling of the transverse field components calls in question Maxwell’s equations, as the most general field distributions. In the aim to preserve their form, the longitudinal and temporal axes are artificially complementarily transformed: | (45) |
Unlike the real functions (39), these two equations are very difficult to be interpreted or understood. Their mutual division gives the speed transformation: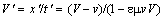 | (46) |
At a wave propagating at the speed V = c, this gives the identity: c' = c. It has been interpreted as the invariant light propagation, irrespective of the frame used.This particular result represents itself the obvious contradiction. It follows from the unfounded starting view, carried out by incorrect revision of the sets (43) & (44). Really, the full above procedure has none a supporting point. Michelson-Morley’s result concerns Earth, as a predominant mass or the preferred reference frame, and cannot be generalized to any other frame. All the remaining ‘proofs’ of SRT also fail in the consistent physical interpretations.
14. Conclusions
One general conclusion from the former inductive elaboration is adopted as the starting point of this exposition. The elaborated and completed EM theory is thus founded as fluid mechanics of the compressible, super-fluidic and inert medium. Main elementary applications of thus renewed theory are demonstrated, confirming thus its former elaboration and the starting view. Some widely accepted speculative results are substituted by essentially distinct, more logical and convincing, mutually compatible, interpretations. Each section contains at least one original idea, new equation, its derivation or interpretation, with the original exposition of the full theory, as the main scientific contribution.Introduced in fluid mechanics – extended into 4D space, all the basic equations of EM theory, as the former phenomenological postulates – in the differential or algebraic forms, are here mere definitions of EM quantities. The three mentioned features of the hypothetical fluid logically determine the static, kinetic and dynamic EM effects, respectively. The two potentials and three fields are introduced by the differential equations, and their mutual algebraic relations are then consequently established. EM theory is thus presented as the central physical discipline, between other such disciplines, from the classical, up to quantum mechanics.
Notes
This Deductive Exposition of EM Theory, founded on an original staring view, may be considered as self-sufficient, at least formally independent of all the former contributions to this theory.
References
| [1] | B. Mišković “Fundamentals of Electrodynamics – Essential Overview of EM Theory” Springer-Verlag, Berlin-Heidelberg, Studies in Computational Inteligence: Selected Topics in Nonlinear Dynamics and Theoretical Electrical Engineering, Volume 459, 2013, pp 234-254, Chapter 13 |

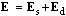 . These two fields are collinear with respective forces, unlike magnetic one, perpendicular to the kinetic (magnetic) forces. The dual treatment understands the two pairs of Maxwell’s equations, determining the two fields. However, one of these equations is trivial and practically excessive.Some stratification of the media – by volume derivation
. These two fields are collinear with respective forces, unlike magnetic one, perpendicular to the kinetic (magnetic) forces. The dual treatment understands the two pairs of Maxwell’s equations, determining the two fields. However, one of these equations is trivial and practically excessive.Some stratification of the media – by volume derivation 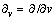 , may be taken for a structural dimension, as the fifth. The domain of observation on this axis is limited from bottom by the value
, may be taken for a structural dimension, as the fifth. The domain of observation on this axis is limited from bottom by the value 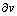 , as the minimal relevant volume. Logarithm of radii of this zooming volume gives two unrestricted legs of the new axis, one of them striving into cosmic widths, and the other – into structural depths. The axis zero is determined by a convenient unit of length. Though distinct from the spatial and temporal axes, this one is formally equal with them. It is more convincing than the widely accepted one, closed into itself on the level of elementary particles, without palpable physical interpretation. With respect to our new axis, apart from the three spatial, and fourth – temporal terms, a 5D continuity equation demands a substantial term, as the fifth, describing structural transformation of the observed substance.EM processes take part in four structural layers: vacuum, dielectric, magnetic and conducting ones. First of them concerns free space or vacuum fields: electric (E) and magnetic (H). The two next layers are substrata of the material field components: polarization (P) and magnetization (M). Respective sums give the two total fields:
, as the minimal relevant volume. Logarithm of radii of this zooming volume gives two unrestricted legs of the new axis, one of them striving into cosmic widths, and the other – into structural depths. The axis zero is determined by a convenient unit of length. Though distinct from the spatial and temporal axes, this one is formally equal with them. It is more convincing than the widely accepted one, closed into itself on the level of elementary particles, without palpable physical interpretation. With respect to our new axis, apart from the three spatial, and fourth – temporal terms, a 5D continuity equation demands a substantial term, as the fifth, describing structural transformation of the observed substance.EM processes take part in four structural layers: vacuum, dielectric, magnetic and conducting ones. First of them concerns free space or vacuum fields: electric (E) and magnetic (H). The two next layers are substrata of the material field components: polarization (P) and magnetization (M). Respective sums give the two total fields: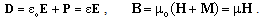
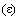 , and magnetic ones – by dynamic
, and magnetic ones – by dynamic 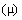 constants. Apart from the medial features, these constants determine the quantities and units. Their two roles are separated by the factorization:
constants. Apart from the medial features, these constants determine the quantities and units. Their two roles are separated by the factorization: 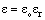 ,
, 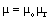 . The vacuum factors harmonize quantities and units, and relative ones express the features of material media.The force fields (E & B) are introduced as the specific actions on respective unit objects, and rational ones (D & H), – as vector densities of respective elementary dipoles. Their asymmetric positions in (1) point to the distinct structural levels of the two EM forces. As if electric forces act at vacuum only, but magnetic ones concern the material layer too. The dimensional equalling of respective fields, by the unit vacuum factors – expressed in natural units, turns these two equations into more symmetric forms.
. The vacuum factors harmonize quantities and units, and relative ones express the features of material media.The force fields (E & B) are introduced as the specific actions on respective unit objects, and rational ones (D & H), – as vector densities of respective elementary dipoles. Their asymmetric positions in (1) point to the distinct structural levels of the two EM forces. As if electric forces act at vacuum only, but magnetic ones concern the material layer too. The dimensional equalling of respective fields, by the unit vacuum factors – expressed in natural units, turns these two equations into more symmetric forms. 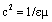 . Internal pressure of the compressible fluid equals to the energy density, and each its disturbance, as the elementary static potential, provides the energy for all other such disturbances, as the objects. This quantity determines the static field, and this field itself – carrying charge:
. Internal pressure of the compressible fluid equals to the energy density, and each its disturbance, as the elementary static potential, provides the energy for all other such disturbances, as the objects. This quantity determines the static field, and this field itself – carrying charge:

 , regular density and pressure disturbance
, regular density and pressure disturbance  gives the density disturbance
gives the density disturbance  . The charges are inseparable from their potentials, and so the two kinetic quantities are collinear. At motion of negative static quantities, these two are opposite. The equation (3a) defines the kinetic potential by motion of static one. Let us now examine their mutual differential relation. Namely, div-operator applied directly to (3a) gives so called Lorentz’ condition, as the continuity equation differentially relating the two EM potentials:
. The charges are inseparable from their potentials, and so the two kinetic quantities are collinear. At motion of negative static quantities, these two are opposite. The equation (3a) defines the kinetic potential by motion of static one. Let us now examine their mutual differential relation. Namely, div-operator applied directly to (3a) gives so called Lorentz’ condition, as the continuity equation differentially relating the two EM potentials: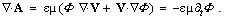
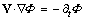 , – in the latter term. This derivative is opposite to the gradient of the moving potential.There is well-known that parallel fluid flows attract, and opposite ones repel each other – by transverse kinetic forces. Magnetic field, representing these forces, is thus defined as the curl of the kinetic potential (5a). In the similar manner, its own curl will soon be identified as the current field, in all the three electric structural layers (5b):
, – in the latter term. This derivative is opposite to the gradient of the moving potential.There is well-known that parallel fluid flows attract, and opposite ones repel each other – by transverse kinetic forces. Magnetic field, representing these forces, is thus defined as the curl of the kinetic potential (5a). In the similar manner, its own curl will soon be identified as the current field, in all the three electric structural layers (5b):
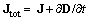 is the total current field consisting of the convection and conduction components – in the former, and displacement one – in the latter terms, at vacuum, conductors and dielectrics, respectively. The magnetic field is transverse to the other two (collinear) vectors. In accord to the relations (3) of the two potentials or carriers, their intermediate quantities can be similarly related. The substitution of (3a) into (5a) gives:
is the total current field consisting of the convection and conduction components – in the former, and displacement one – in the latter terms, at vacuum, conductors and dielectrics, respectively. The magnetic field is transverse to the other two (collinear) vectors. In accord to the relations (3) of the two potentials or carriers, their intermediate quantities can be similarly related. The substitution of (3a) into (5a) gives: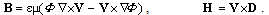
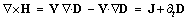

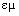 – consequently replaced. The negative signs point to the attractive (or repulsive) interactions. Grad applied to (7a), after missing of the spatial derivatives of the object speed, gives respective field:
– consequently replaced. The negative signs point to the attractive (or repulsive) interactions. Grad applied to (7a), after missing of the spatial derivatives of the object speed, gives respective field: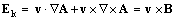

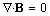 . It only speaks against the existence of any free magnetic poles, being possibly predicted in advance.The kinetic potential and magnetic field are the two perpendicular vortical fields, and their gradient, perpendicular to the common surface, is a non-vortical field. The motion in this direction varies the potential on the object, and – with respect to (9a), induces some dynamic field:
. It only speaks against the existence of any free magnetic poles, being possibly predicted in advance.The kinetic potential and magnetic field are the two perpendicular vortical fields, and their gradient, perpendicular to the common surface, is a non-vortical field. The motion in this direction varies the potential on the object, and – with respect to (9a), induces some dynamic field: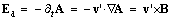
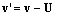 is transverse mutual (charge-field) speed. In the observed direction:
is transverse mutual (charge-field) speed. In the observed direction: 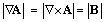 . Really, in the opposite sense, curl applied to (10) gives (9b):
. Really, in the opposite sense, curl applied to (10) gives (9b):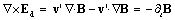
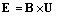 . Together with the kinetic one (6b), it forms the convective pair of J. J. Thomson. With respect to above procedures, neglecting all spatial derivatives of the field speeds, this pair is restricted to the uniform rectilinear motion. With the additional restriction of the speed direction in (10), these two relations seemed to be very problematic. The restrictions were the reasons of their missing from the standard EM theory.
. Together with the kinetic one (6b), it forms the convective pair of J. J. Thomson. With respect to above procedures, neglecting all spatial derivatives of the field speeds, this pair is restricted to the uniform rectilinear motion. With the additional restriction of the speed direction in (10), these two relations seemed to be very problematic. The restrictions were the reasons of their missing from the standard EM theory.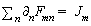
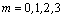 is the ordinal number of equation, with the summation performed per the index
is the ordinal number of equation, with the summation performed per the index 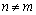 . The charge carried by cosmic expansion along t-axis forms respective current component (J0). All the separate field components (Fmn) are identified by the following tensor:
. The charge carried by cosmic expansion along t-axis forms respective current component (J0). All the separate field components (Fmn) are identified by the following tensor: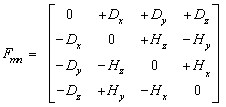

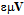 gives (12b). The same result can be obtained from (5). The two temporal terms accord to the dynamic, and spatial ones – to static fields. With respect to above procedure, the equations (2,5-b) understand both – static and dynamic field components, speaking thus in favour of their unity. To confirm this, let us compose the 4D potential, as the fluid flows of the two orthogonal components, from the temporal and spatial domains:
gives (12b). The same result can be obtained from (5). The two temporal terms accord to the dynamic, and spatial ones – to static fields. With respect to above procedure, the equations (2,5-b) understand both – static and dynamic field components, speaking thus in favour of their unity. To confirm this, let us compose the 4D potential, as the fluid flows of the two orthogonal components, from the temporal and spatial domains: 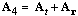 . With respect to the electric field components (2,9-a), their sum gives the following united mathematical form:
. With respect to the electric field components (2,9-a), their sum gives the following united mathematical form: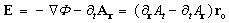
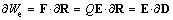
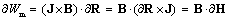

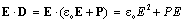
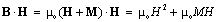
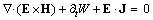
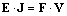 . This dissipation may be understood as energy dislocation along the fifth axis, from one into another structural layers.The cross product of the two fields, in the spatial term, represents the current field of EM energy:
. This dissipation may be understood as energy dislocation along the fifth axis, from one into another structural layers.The cross product of the two fields, in the spatial term, represents the current field of EM energy: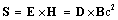
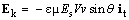
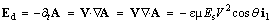
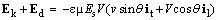
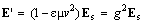
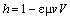 . With some formal inconsistencies and fantastic interpretations, the two factors play the crucial roles in foundation of SRT.Moving EM fields carry by themselves respective energies. The two convective fields,
. With some formal inconsistencies and fantastic interpretations, the two factors play the crucial roles in foundation of SRT.Moving EM fields carry by themselves respective energies. The two convective fields, 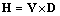 &
& 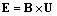 , substituted into Poynting’s relation (18), express the two energetic currents, electric and magnetic ones:
, substituted into Poynting’s relation (18), express the two energetic currents, electric and magnetic ones: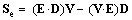
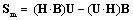
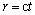 . The radius (r) concerns the wave cross-section in the plain of propagation. With respect to Poynting’s relation (18), the speed of EM wave propagation is determined by the ratio of the energetic and equivalent mass currents, as the two collinear flows, being perpendicular to both EM fields:
. The radius (r) concerns the wave cross-section in the plain of propagation. With respect to Poynting’s relation (18), the speed of EM wave propagation is determined by the ratio of the energetic and equivalent mass currents, as the two collinear flows, being perpendicular to both EM fields: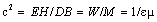
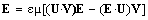

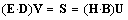


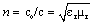 , as the ratio of the speeds of wave propagation through vacuum and matter.On the other hand, the arithmetic average of the two sides of (27) explicates the wave propagation:
, as the ratio of the speeds of wave propagation through vacuum and matter.On the other hand, the arithmetic average of the two sides of (27) explicates the wave propagation: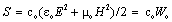
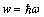 – from 3D, obtains continual values. On the other hand, with respect to the vacuum fluid and particles, constituting the expanding matter, light propagation is related to this matter, as the moving medium.
– from 3D, obtains continual values. On the other hand, with respect to the vacuum fluid and particles, constituting the expanding matter, light propagation is related to this matter, as the moving medium.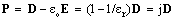
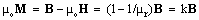
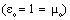 . Fresnel’s incorrect factor,
. Fresnel’s incorrect factor, 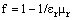 , is reduced into one of these two, at exclusively dielectric or magnetic media.The material fields are continued by similar associated fields, in the surroundings. Moving together with the medial body, these fields produce dissimilar convective inductions, superimposed to the given fields:
, is reduced into one of these two, at exclusively dielectric or magnetic media.The material fields are continued by similar associated fields, in the surroundings. Moving together with the medial body, these fields produce dissimilar convective inductions, superimposed to the given fields:
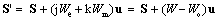
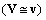 , the kinetic central forces, opposite to the static ones, may be expressed by the symmetric equation (34b):
, the kinetic central forces, opposite to the static ones, may be expressed by the symmetric equation (34b):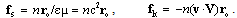
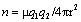 simplifies the equations. Its integration along the radii gives the factor
simplifies the equations. Its integration along the radii gives the factor 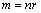 , turning thus the forces into energies:
, turning thus the forces into energies: 
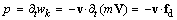

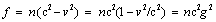
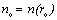 – at rest, this force strives to expand the particle. Therefore, at all the speeds, it must be opposed by a constant external pressure (fo), determined at rest. The balance (f = fo) gives the following two equalities:
– at rest, this force strives to expand the particle. Therefore, at all the speeds, it must be opposed by a constant external pressure (fo), determined at rest. The balance (f = fo) gives the following two equalities: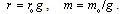
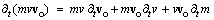
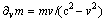 , this gives the two forces, centrifugal and inertial ones:
, this gives the two forces, centrifugal and inertial ones: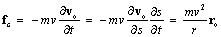
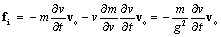
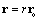 is the path curvature radius. Both forces are additionally scaled – due to the variable mass. Instead of the two different masses, the two forces are in fact the distinct functions of the same variable mass. The former force strives only to the strait direction of the motion, but the latter one changes the energy of a moving body. A moving charge is considered as the invariant quantity. However, if the definition (2b), apart from the static – concerns the dynamic field (20), with the invariant transverse components, there is the charge function:
is the path curvature radius. Both forces are additionally scaled – due to the variable mass. Instead of the two different masses, the two forces are in fact the distinct functions of the same variable mass. The former force strives only to the strait direction of the motion, but the latter one changes the energy of a moving body. A moving charge is considered as the invariant quantity. However, if the definition (2b), apart from the static – concerns the dynamic field (20), with the invariant transverse components, there is the charge function: 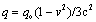 . At the upper boundary speed of the particle motion (v = c), it would be reduced in the ratio 2/3. Just this value is known from the quark theory. Instead of its dividing, the charge is here diminished. From transverse directions, however, the charge seems to be the invariant quantity.
. At the upper boundary speed of the particle motion (v = c), it would be reduced in the ratio 2/3. Just this value is known from the quark theory. Instead of its dividing, the charge is here diminished. From transverse directions, however, the charge seems to be the invariant quantity.

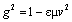 , accidentally equal to the factor contained in the function (38), points to essential inequality of the two frames, speaking thus in favour of the privileged status of some local frame.For the sake of the frame equivalence, SRT distributed this factor, by g–1 in each of the sets. This scaling of the transverse field components calls in question Maxwell’s equations, as the most general field distributions. In the aim to preserve their form, the longitudinal and temporal axes are artificially complementarily transformed:
, accidentally equal to the factor contained in the function (38), points to essential inequality of the two frames, speaking thus in favour of the privileged status of some local frame.For the sake of the frame equivalence, SRT distributed this factor, by g–1 in each of the sets. This scaling of the transverse field components calls in question Maxwell’s equations, as the most general field distributions. In the aim to preserve their form, the longitudinal and temporal axes are artificially complementarily transformed:
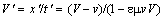
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML