-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Electromagnetics and Applications
p-ISSN: 2168-5037 e-ISSN: 2168-5045
2013; 3(2): 15-19
doi:10.5923/j.ijea.20130302.02
Resonant Degenerate Crystal Made of Spheres Located in Magnetodielectric Medium
Anatoliy I. Kozar
Kharkov National University of Radio Electronics, Kharkov, Ukraine
Correspondence to: Anatoliy I. Kozar, Kharkov National University of Radio Electronics, Kharkov, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The paper addresses the computational method we proposed to analyze the phenomena which occur when electromagnetic waves are scattered by a finite resonant crystal with a cubic lattice having small resonant magnetodielectric spheres in its nodes. The method is based on the second kind Fredholm integral equations. Properties of the degenerate resonant crystal are investigated when it is located in magnetodielecrtic media with either positive or negative values of permittivity ε0 and permeability μ0. It is shown that media with positive and negative values of permittivity and permeability differently influence on scattering properties of the degenerate resonant crystal. When the permittivity and permeability jump, the effect of its degeneration cancellation is found such that the lattice resonance and the internal crystal sphere resonance are no more coincident, and the resonance curves split. Graphic dependences given in the paper numerically define a magnitude of the splitting. The influence of the presence of a cavity in the resonant crystal on a structure of the scattered field in the Fresnel zone is graphically estimated.
Keywords: Magnetodielectric, Integral Equation, Crystal
Cite this paper: Anatoliy I. Kozar, Resonant Degenerate Crystal Made of Spheres Located in Magnetodielectric Medium, International Journal of Electromagnetics and Applications, Vol. 3 No. 2, 2013, pp. 15-19. doi: 10.5923/j.ijea.20130302.02.
1. Introduction
- Our attention was attracted by works[1-6] wherein unusual properties of substances with simultaneously negative values of permittivity ε and permeability μ were considered. It is of interest to study scattering properties of a finite discrete resonant crystal made of magnetodielectric spheres, if the crystal is located in external media with simultaneously either positive or negative permittivity ε and permeability μ. Investigated in this paper are the crystal properties when the degenerate resonance (st+m+e) is excited in it, which occurs when the structural (lattice) crystal resonance (st) coincides with the internal magnetic (m) and electric (e) resonances of spheres (also coincided). We study the case being equivalent to that of roentgen crystals optics, with
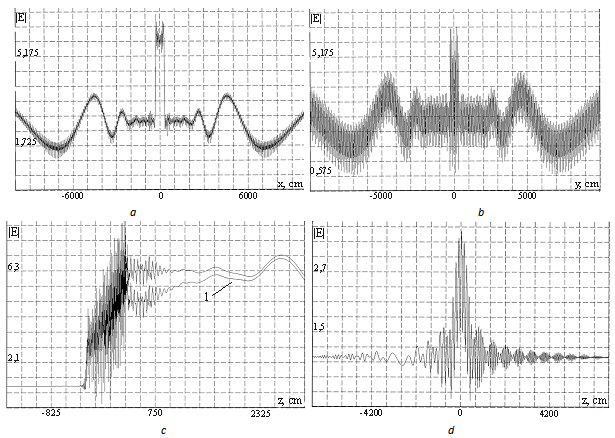
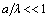 ;
;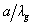 ~1;
~1; 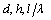 ~1 where
~1 where 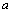 is the sphere radius;
is the sphere radius; 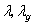 are the lengths of the waves scattered outside and inside the spheres;
are the lengths of the waves scattered outside and inside the spheres; 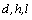 are the orthogonal lattice constants. We have investigated the multimode structure (d, h, l~
are the orthogonal lattice constants. We have investigated the multimode structure (d, h, l~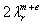 ) of the resonant (r) field inside and outside the cubic lattice in the Fresnel and Fraunhofer zones for external media with the permittivity and permeability
) of the resonant (r) field inside and outside the cubic lattice in the Fresnel and Fraunhofer zones for external media with the permittivity and permeability 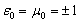 . An effect of the resonant crystal degeneracy cancellation is considered. The solution is obtained on the basis of the second type Fredholm integral electromagnetic equations[7, 8,9].
. An effect of the resonant crystal degeneracy cancellation is considered. The solution is obtained on the basis of the second type Fredholm integral electromagnetic equations[7, 8,9].2. Theoretical Details
- Let us find the field scattered over the known internal field of scatterers via the electric
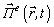 and magnetic
and magnetic 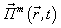 Hertz potentials of the spatial lattice
Hertz potentials of the spatial lattice 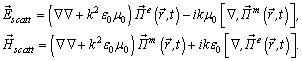 | (1) |
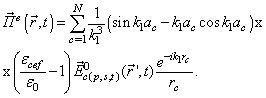 | (2) |
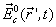 is the induced internal field of the interacting spheres. The field can be found via the algebraic system of inhomogeneous equations[3],
is the induced internal field of the interacting spheres. The field can be found via the algebraic system of inhomogeneous equations[3], 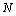 is the number of spheres. The field scattered by the system of spheres
is the number of spheres. The field scattered by the system of spheres 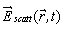 is found via (1), (2) as
is found via (1), (2) as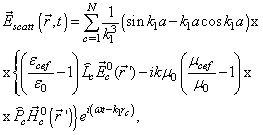 | (3) |
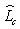 and
and 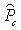 are the functional matrices
are the functional matrices 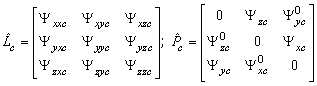 The element
The element 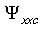 of the matrix
of the matrix 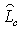 is
is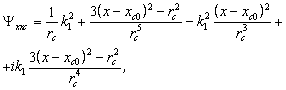 where
where 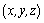 are the coordinates of the observation point;
are the coordinates of the observation point; 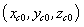 are the coordinates of the spheres’ centres.The expression (3) describes the scattered field that consists of propagating and damped spatial harmonics inside and outside the lattice in the Fresnel and Fraunhofer zones.The entire field at an arbitrary medium point outside the spheres is defined as
are the coordinates of the spheres’ centres.The expression (3) describes the scattered field that consists of propagating and damped spatial harmonics inside and outside the lattice in the Fresnel and Fraunhofer zones.The entire field at an arbitrary medium point outside the spheres is defined as 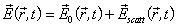 | (4) |
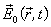 is the undisturbed field of the scattered wave. The expressions (3) and (4) are numerically analysed for the degenerate resonant cubic crystal. The analysis results are given in Figs. 1, 2, 3. The number of spheres here is N = 64000; their radii are а = 0.5 cm; their permittivity and permeability are
is the undisturbed field of the scattered wave. The expressions (3) and (4) are numerically analysed for the degenerate resonant cubic crystal. The analysis results are given in Figs. 1, 2, 3. The number of spheres here is N = 64000; their radii are а = 0.5 cm; their permittivity and permeability are 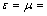 9.75; the lattice constants are
9.75; the lattice constants are 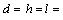
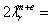 14.82 cm (Fig. 1 a) and
14.82 cm (Fig. 1 a) and 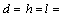
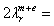 12.52 cm (Fig. 1 b).Figs. 1 а and 1 b show the fields modules, (4) and (3), versus scattered wavelength λ for the degenerate resonant crystals in the medium with
12.52 cm (Fig. 1 b).Figs. 1 а and 1 b show the fields modules, (4) and (3), versus scattered wavelength λ for the degenerate resonant crystals in the medium with 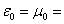 +1 (curve 1, Fig. 1 a) and in the medium with
+1 (curve 1, Fig. 1 a) and in the medium with 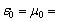 –1 (curve 1, Fig. 1 b), respectively. Considered for the same crystals are also the same dependences for the cases when the medium parameters vary and become
–1 (curve 1, Fig. 1 b), respectively. Considered for the same crystals are also the same dependences for the cases when the medium parameters vary and become 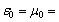 –1 (curve 2 in Fig. 1 a) and
–1 (curve 2 in Fig. 1 a) and 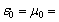 +1 (curve 2 in Fig. 1 b). Here resonances of lattices and spheres do not coincide. Figs. 2 a,b and 3 a,b show field modules, (4) and (3) , versus changes in coordinates x, y, respectively, in the direction of scattered wave propagation (like in Fig. 1 b), inside (when x and y are in the vicinity of zero) and outside the degenerate crystal in media with
+1 (curve 2 in Fig. 1 b). Here resonances of lattices and spheres do not coincide. Figs. 2 a,b and 3 a,b show field modules, (4) and (3) , versus changes in coordinates x, y, respectively, in the direction of scattered wave propagation (like in Fig. 1 b), inside (when x and y are in the vicinity of zero) and outside the degenerate crystal in media with 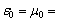 +1 (Fig. 2 a,b) and
+1 (Fig. 2 a,b) and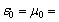 –1 (Fig. 3 a,b). Figs. 2 с and 3 с show the damped component of the multimode scattered field in the Fresnel zone in media with
–1 (Fig. 3 a,b). Figs. 2 с and 3 с show the damped component of the multimode scattered field in the Fresnel zone in media with 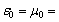 +1 (Fig. 2 с), and
+1 (Fig. 2 с), and 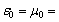 –1 (Fig. 3 с). Curve 1 is in both figures relates to crystals with internal cavities[10,11].
–1 (Fig. 3 с). Curve 1 is in both figures relates to crystals with internal cavities[10,11]. 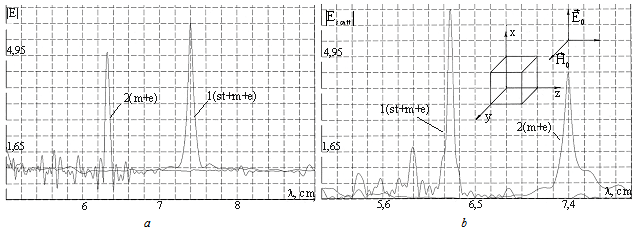 | Figure 1. Dispersion dependences of entire (a) and scattered (b) fields in media with 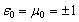 |
 | Figure 2. The entire field in the medium with 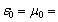 +1 +1 |
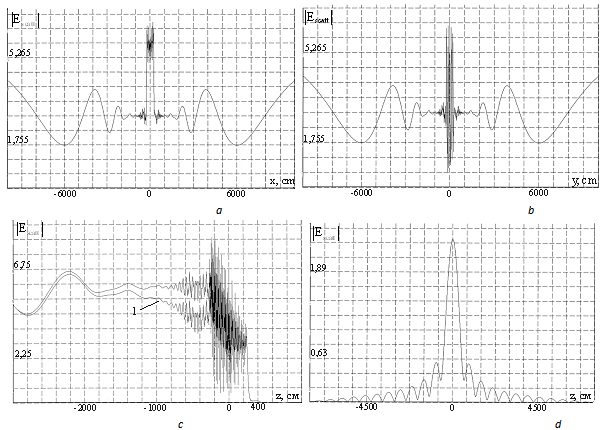 | Figure 3. The field scattered in a medium with 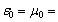 –1. –1. |
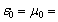 +1 (Fig. 2 d) and
+1 (Fig. 2 d) and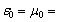 –1 (Fig. 3 d).It follows from the numerical analysis that the resonant degenerate cubic crystal in media with simultaneously either positive or negative permittivity and permeability
–1 (Fig. 3 d).It follows from the numerical analysis that the resonant degenerate cubic crystal in media with simultaneously either positive or negative permittivity and permeability 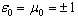 has different electromagnetic properties. In a medium with
has different electromagnetic properties. In a medium with 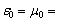 –1 the crystal has the pronounced reflecting properties. It can play a role of reflector and resonator with a strong internal field. By forming nodes and antinodes on crystal faces, one can control the scattering properties of the crystal. In a medium with
–1 the crystal has the pronounced reflecting properties. It can play a role of reflector and resonator with a strong internal field. By forming nodes and antinodes on crystal faces, one can control the scattering properties of the crystal. In a medium with 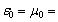 +1, a phenomenon of resonant propagation of the scattered wave is inherent in the crystal. This can be used when creating non-reflecting devices.By varying the medium parameters
+1, a phenomenon of resonant propagation of the scattered wave is inherent in the crystal. This can be used when creating non-reflecting devices.By varying the medium parameters 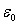 and
and 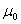 , the effect of degeneracy cancellation in the resonance degenerate crystal can be obtained, which entails violation of the crystal resonances (st+ m +e) superposition. As an example, this effect is shown in Fig.4 where one can see resonant curves splitting as a consequence of the effect shown in Fig.1 b , and occurrence of noncoincident resonances (st), (m), (e) (Fig. 4 a) and (e), (m) (Fig. 4 b). In the case of resonance curve 1 (st+ m +e) splitting in Fig. 4 a , parameters of the medium have the values:
, the effect of degeneracy cancellation in the resonance degenerate crystal can be obtained, which entails violation of the crystal resonances (st+ m +e) superposition. As an example, this effect is shown in Fig.4 where one can see resonant curves splitting as a consequence of the effect shown in Fig.1 b , and occurrence of noncoincident resonances (st), (m), (e) (Fig. 4 a) and (e), (m) (Fig. 4 b). In the case of resonance curve 1 (st+ m +e) splitting in Fig. 4 a , parameters of the medium have the values: 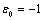 ;
; 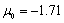 . After the degeneracy is cancelled, the structural resonance (st) of curve 1 (st+ m +e) (Fig. 4 а) shifts to the domain of the wavelength
. After the degeneracy is cancelled, the structural resonance (st) of curve 1 (st+ m +e) (Fig. 4 а) shifts to the domain of the wavelength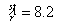 , and therefore is not presented in Fig. 4a, as it is beyond the figure limit. In the case of curve 1 (m + e) splitting in Fig. 4 b , the medium parameters have the values:
, and therefore is not presented in Fig. 4a, as it is beyond the figure limit. In the case of curve 1 (m + e) splitting in Fig. 4 b , the medium parameters have the values: 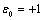 ;
; 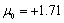 .
.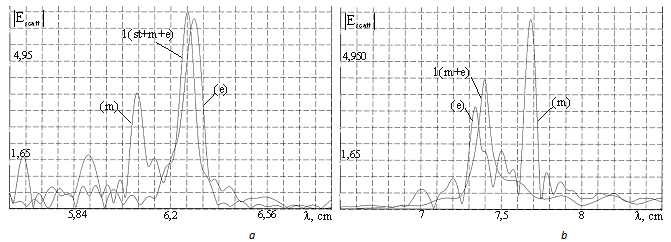 | Figure 4. The influence of environment on cancellation of the resonant cubic crystal degeneracy |
3. Conclusions
- The resonant degenerate crystal located in a magnetodielectric medium with varying parameters
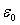 and
and 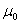 can be used for creation of resonant metastructures with abnormal electromagnetic properties.
can be used for creation of resonant metastructures with abnormal electromagnetic properties.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML