Hicham Megnafi, Noureddine Boukli Hacene
Telecommuniation Laboratory of Tlemcen, Univ-Abou Bakr Belkaid, B.P N 119, Tlemcen, Algeria
Correspondence to: Hicham Megnafi, Telecommuniation Laboratory of Tlemcen, Univ-Abou Bakr Belkaid, B.P N 119, Tlemcen, Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper presents an efficient execution of the Wave Concept Iterative Procedure algorithm (WCIP) combined with the Multi-scale approach’s module (M.WCIP). This approach is introduced to solve the problem of the relationship between circuit complexity and computation time. Therefore, this work consists of a development of simulation software based on this combination for planar circuits very jagged structure’s simulation. The two layouts of the micro-strip trisection filter’s simulation are made. The first layout has a higher selectivity on the high side of the pass-band and the second has a higher selectivity but on the low side of the pass-band. The results obtained the WCIP and M.WCIP are analyzed and validated by comparison with results obtained by other researchers.
Keywords:
Iterative Method, Microwave, Concept of Waves, Sparameter, Microstrip Trisection Filter, Multi-scale
Cite this paper: Hicham Megnafi, Noureddine Boukli Hacene, An Efficient Analysis of Microstrip Trisection Filters Using an Iterative Method Combined by Approach Multi-Scale, International Journal of Electromagnetics and Applications, Vol. 3 No. 2, 2013, pp. 9-14. doi: 10.5923/j.ijea.20130302.01.
1. Introduction
The greater compactness and the gradual integration of electronic devices in a smaller location introduced to a very high resolution in the spatial domain in order to describe the circuit correctly when using the classical iterative method. The increasing of this resolution creates a big need for large memory resources and particularly with a long computation time[1]. For example, if the space-step is reduced by two, the storage conditions are multiplied by eight in the differential methods[2]. Therefore, a comprehensive analysis must be developed to effectively undo the relationship between circuit complexity and the resolution of the spatial domain. The solution to this problem can be obtained by using multi-grid levels or multi-resolution approach.There are few examples in the literature concerning the techniques of spatial multi-scale approach. However, there are few articles concerning the multi-grid, such as "multigrid TLM method"[3][4]. This other form of spatial multi-resolution is also used in order to describe the system more finely. Similarly, the multi-scale technique presented in the article "sketch algorithm" by G. Deng[5] allows to decompose an image into 3 levels using a wavelet transform.The multi-scale approach is not usually exploited, but here it is used in an iterative method. This approach enables an accurate global analysis of planar circuits usually characterized by jagged structures. The iterative method formulation[6][7] is based on iterative relations between incident and reflected waves: one takes into account boundary conditions in the spatial domain, and the other the reaction of the environment in the spectral domain. Convergence is reached progressively through iterations [8][2].In this work, we present roughly the usual iterative procedure. Then we are devoted to the justification of the multi-scale approach use. The results are given and discussed afterwards.
2. Iterative Method
In this paragraph, we introduce the definitions of all important values in order to present the WCIP principle.
2.1. Waves Definition
The WCIP is developed in terms of waves, which are defined as a combination of the electric field 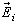 and the transverse current density
and the transverse current density 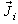 in terms of incident waves and reflected waves[6].These incident
in terms of incident waves and reflected waves[6].These incident 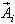 and reflected
and reflected 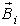 at the boundaries interfaces on one side Ω. These waves are described by the following formulation[7]:
at the boundaries interfaces on one side Ω. These waves are described by the following formulation[7]: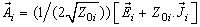 | (1) |
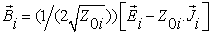 | (2) |
With: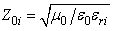 Where, Z0i is the intrinsic impedance of the medium,
Where, Z0i is the intrinsic impedance of the medium, 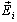 is the tangential electric field,
is the tangential electric field, 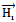
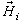 is the tangential magnetic field and
is the tangential magnetic field and 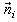 is the unit vector normal to Ω and directed into region i ( i = 1 or 2).
is the unit vector normal to Ω and directed into region i ( i = 1 or 2).
2.2. WCIP Principle
According to the criterion defining the wave concept, we can define the electric field and the current density values in each point of the surface Ω by the determination of the incident waves and the reflective waves values. So, the iterative process is based on the creation of a recurrence relation between the incident waves and the reflective waves, and the repetition of this relation until obtaining the problem solution.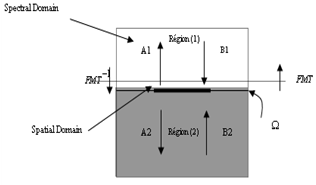 | Figure 1. Processus itératif |
The iterative method can be summarized by the following equations system[8]: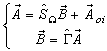 | (5) |
With: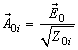 Where,
Where, 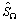 is the diffraction operator in the interface,
is the diffraction operator in the interface, 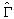 the reflection operator on the covers,
the reflection operator on the covers, 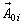 is the wave creates by the source in the space field and
is the wave creates by the source in the space field and 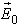 the total electric field produces by the excitation source.
the total electric field produces by the excitation source.
3. Multi-Scale
Sometimes taking into account a certain mesh size, the structure studied can be represented by totally metallic or dielectric pixels, as in the case where the circuit dimensions are imposed. To be rigorous, some pixels must be partly metallic or dielectric; those are c that is replaced by surface impedances. This involves local modifications of the spatial diffraction operator; this is called multi-scale[1][2]. This principle is illustrated in Figure 2.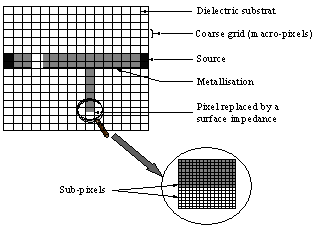 | Figure 2. Multi-Scale Principle |
The study of macro-pixels which are partially metallic and dielectric regardless of the circuit has become possible because the fundamental mode alone is sufficient to describe the interaction between macro-pixel neighbors. The influence of higher order modes is negligible. Indeed, the higher harmonics created by abrupt discontinuity have an energy that is localized in its Neighborhood[1][9][10]. However, within a macro-pixel, sub-pixels are interacting between them. Finally, the macro-pixel is replaced by a surface impedance that characterizes this part of the circuit.
3.1. Determination of Equivalent Surface Impedance of the Macro-pixels
To calculate the surface impedance, we suppose that the macro-pixel constitutes an iris in waveguides with periodic walls as it is described in Figure 3. 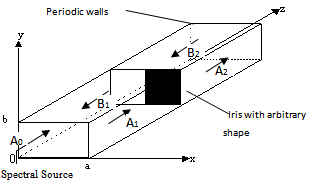 | Figure 3. Iris in periodic waveguide |
The new boundary conditions involve a novel definition of the FMT. In the traditional waveguide, the lateral walls are electric or magnetic and the FMT has an expression in sines and cosines. With periodic condition, we use FMT with exponential development[7]. The studied structure is excited by a spectral wave A0 and the surface impedance is deduced from the ratio of the electric and magnetic fields. Moreover, we can define two different types of macro-pixels; a unidirectional or a complex iris.
3.2. Definition of Diffraction Operator on the Sub-pixels
According to equivalent surface impedance of iris that was calculates by iterative process, we can deduce the relationship between the fields (E1, E2) and the current densities (J1, J2)[11]: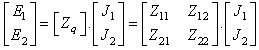 | (5) |
The relationship between incident and reflected waves on particular macro-pixels can be obtained by equation (6). 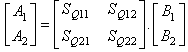 | (6) |
With: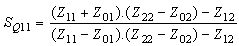 | (7) |
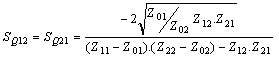 | (8) |
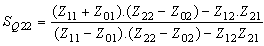 | (9) |
Where: 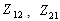 is the value of impedance matrix of iris. The new formula of the diffraction operator can be obtained by the equation (10).
is the value of impedance matrix of iris. The new formula of the diffraction operator can be obtained by the equation (10).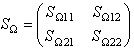 | (10) |
With[11]: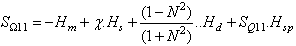 | (11) |
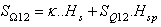 | (12) |
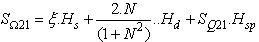 | (13) |
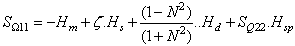 | (14) |
Where: Hm, Hd, Hs and Hsp are indicating functions of the metal, dielectric, source and Iris mediums. χ, κ, ξ, ζ depend on the type of used source[8].
4. Multi-scale WCIP Algorithm
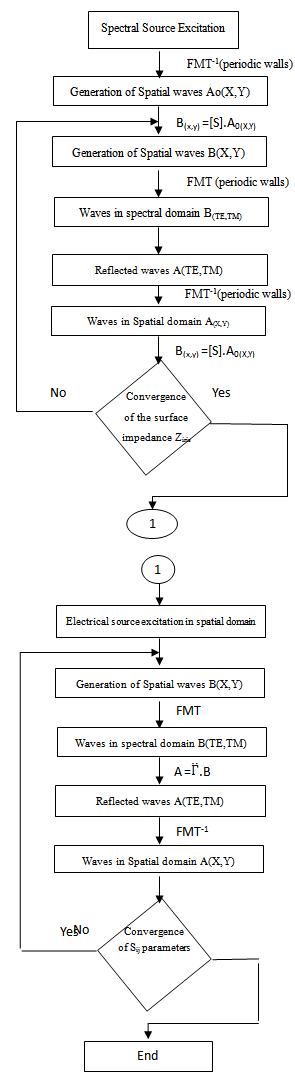 | Figure 4. Multi-scale.WCIP Algorithm[11] |
5. Results
In this section, tow layouts of the micro-strip trisection filter are utilized for validation of the iterative method algorithm classic (WCIP) and a new formulation of this method (M.WCIP).The first layout has a higher selectivity on the high side of the pass-band and the second has a higher selectivity but on the low side of the pass-band. Our obtained results will be compared with another work cited in[12].
5.1. Micro-strip Trisection Filter : Layout One Simulated by WCIP Classic
The application example that we simulate is a Layout of the micro-strip trisection filter designed to have a higher selectivity on the high side of the pass-band. It is showed in figure 5. This layout is simulated by iterative method algorithm classic WCIP with 512x512 pixels.The layout of the designed micro-strip trisection filter with the dimensions on a substrate has a relative dielectric constant of 10.8 and a thickness of 1.27 mm. The size of the filter is about 0.19 λ0 by 0.27 λ0, where λ0 is the guided wavelength of a 50 ohm line on the substrate at the mid band frequency. This size is evidently very compact. 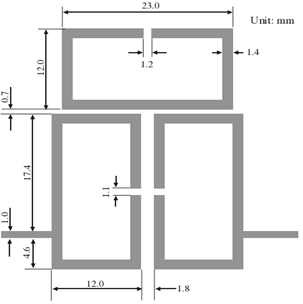 | Figure 5. Layout of the microstrip trisection filter designed to have a higher selectivity on high side of the passband |
Figure 6 shows the frequency responses of the micro-strip trisection filter obtained by iterative method classic WCIP and by[12]. We notice that there is a good agreement between our simulation results by WCIP and according to the results presented in[12].
5.2. Micro-strip Trisection Filter: Layout Two Simulated by M.WCIP
The application example that we simulate is a Layout of the micro-strip trisection filter designed to have a higher selectivity on low side of the pass-band. Figure 7 shows the layout of the designed filter with all dimensions on a substrate having a relative dielectric constant of 10.8 and a thickness of 1.27 mm. The size of the filter amounts to 0.41 λg0 by 0.17 λg0. This layout is simulated by new formulation of iterative method algorithm M.WCIP with 128x128 pixels.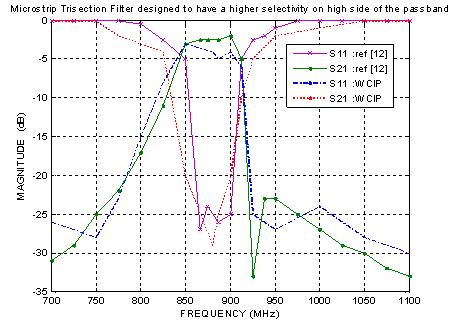 | Figure 6. Simulated frequency responses S21 and S11 of the the microstrip trisection filter designed to have a higher selectivity on high side of the passband.obtained by WCIP and by[12] |
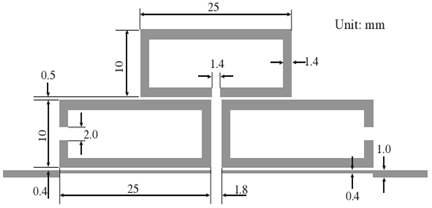 | Figure 7. Layout of the microstrip trisection filter designed to have a higher selectivity on low side of the passband |
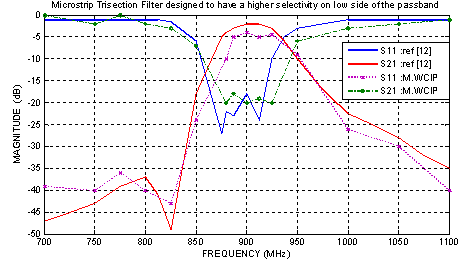 | Figure 8. Simulated frequency responses S21 and S11 of the the microstrip trisection filter designed to have a higher selectivity on low side of the passband |
The transmission coefficient and the reflection variation according to the frequency are presented in figure 8. We notice that there is a good agreement between our simulation results by M.WCIP and according to the results presented in[12].This result was shown that this multi-scale method can be used to increase resolution and to reduce the calculation time and the computer storage.
6. Conclusions
The development of a multi-scale iterative method based on the wave concept has been described here. The obtained results are of similar accuracy compared to those of a uniform fine mesh and with results obtained by other researchers. It was shown that this multi-scale method can be used to increase resolution and to reduce the calculation time and the computer storage. The same principles described here can be transferred to other methods with success.
References
| [1] | N’gongo, R.S., and Baudrand, H.: "Application of wave concept iterative procedure in planar circuit ", Recent Res. Devel. Microw.Theory Tech., 1999, 1, pp. 187–197 |
| [2] | L. Cohen, R.S. N’Gongo, R. Garcia and H. Baudrand, "Equivalent impedance boundary conditions for refined meshes applied to planar circuits ", IEE Proc.-Microw. Antennas Propag., Vol. 150, No. 4, August 2000 |
| [3] | Herring, J.L., and Christopoulos, C., "Multigrid Transmission Line Modelling method for solving Electromagnetic field problems ", Electron. Lett., 1990, 26, (20) , pp. 1794–1795 |
| [4] | Wlodarczyk, J, "New multigrid interface for the TLM method ", Electron. Lett., 1996, 32, (12), pp. 1111–1112 |
| [5] | Deng, G. , "Grey scale image representation using binary sketch image ", Electron. Lett., 1996, 32, (10), pp. 881–882 |
| [6] | N’gongo, R.S., and Baudrand, H, "Application of wave concept iterative procedure in planar circuit ", Recent Res. Devel. Microw. Theory Tech., 1999, 1, pp. 187–197 |
| [7] | Sboui N., A.Gharsallah, H. Baudrand, et A. Gharbi, " Analysis of double-loop meander line by using an iterative process ", Microwave and optical technology letters/vol. 26, no. 6, September 20 2000. |
| [8] | Fontgalland G., P.I.L.Ferreira, T.-P.Vuong, N.Raveu et H.Baudrand, " Analysis of asymmetric PBG ground planes for wireless communications", IEEE Explore 0-7803-9342-2/05, November 2008 |
| [9] | H. Baudrand, N. Raveu and N. Sboui , "Applications of Mulitscale Waves Concept Iterative Procedure ", IEEE transactions on microwave theory and techniques, Vol.53, n°1, pp 200-213, January 2005. |
| [10] | F. Surre, L. Cohen, and H. Baudrand, " New approach for multi-scale circuit analysis ", 31th European Microwave Conference (EUMC), Lenders, Royaume-Uni, September 2001. |
| [11] | H. Zairi, A. Gharsallah, A. Gharbi and H. Baudrand , " Analysis of planar circuits using a multigrid iterative method ", IEE Proc.-Microw. Antennas Propag., Vol. 153, No. 3, June 2006 |
| [12] | Jia-Sheng Hong, M. J. Lancaster, " Microstrip Filters for RF/Microwave Applications ", John Wiley & Sons, Inc., 2001, pp 335-341 |

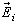 and the transverse current density
and the transverse current density 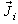 in terms of incident waves and reflected waves[6].These incident
in terms of incident waves and reflected waves[6].These incident 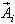 and reflected
and reflected 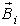 at the boundaries interfaces on one side Ω. These waves are described by the following formulation[7]:
at the boundaries interfaces on one side Ω. These waves are described by the following formulation[7]: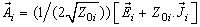
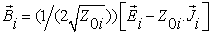
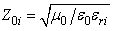 Where, Z0i is the intrinsic impedance of the medium,
Where, Z0i is the intrinsic impedance of the medium, 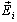 is the tangential electric field,
is the tangential electric field, 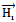
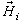 is the tangential magnetic field and
is the tangential magnetic field and 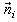 is the unit vector normal to Ω and directed into region i ( i = 1 or 2).
is the unit vector normal to Ω and directed into region i ( i = 1 or 2).
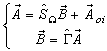
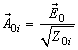 Where,
Where, 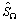 is the diffraction operator in the interface,
is the diffraction operator in the interface, 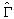 the reflection operator on the covers,
the reflection operator on the covers, 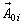 is the wave creates by the source in the space field and
is the wave creates by the source in the space field and 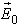 the total electric field produces by the excitation source.
the total electric field produces by the excitation source.

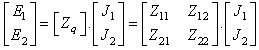
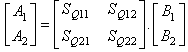
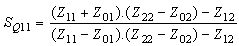
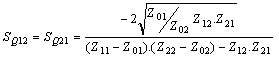
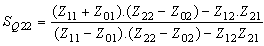
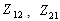 is the value of impedance matrix of iris. The new formula of the diffraction operator can be obtained by the equation (10).
is the value of impedance matrix of iris. The new formula of the diffraction operator can be obtained by the equation (10).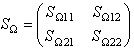
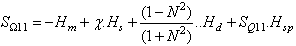
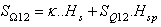
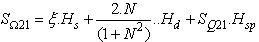
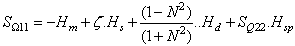




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML