1. Introduction

There has been a growing interest in different configurations of coplanar waveguide (CPW) transmission line such as conductor backed CPW, CPW with finite ground width, shielded multilayer CPW, elevated or suspended CPW, asymmetric CPW etc. The CPW offers many advantages over microstrip line such as easy connection of both series and shunt components without drilling holes through the dielectric substrate, less dispersive and provides ease of controlling the characteristics of line by changing the strip and slot width. Therefore, CPW transmission lines are widely used in the design of components and interconnect in modern microwave circuit design. The accurate modelling of transmission lines is important in the design and development of modern integrated circuits. Most research done in literature on CPW was based under the assumption of zero conductor thickness using the conformal mapping and spectral domain approach (SDA) method. But in practical cases, the conductor thickness can not be zero and affects the impedance, effective dielectric constant and losses etc. Several research papers have been presented to characterize planar transmission line structure with finite metallization thickness[1-13].

This paper presents the effects of finite strip thickness on the impedance, effective relative permittivity, dielectric loss and conductor loss of multilayer CPW structures using quasi-static SDA method on isotropic dielectric substrate. Dispersion characteristics of multilayer CPW is also analysed using single layer reduction (SLR) method.

2. Coplanar Waveguide Analysis

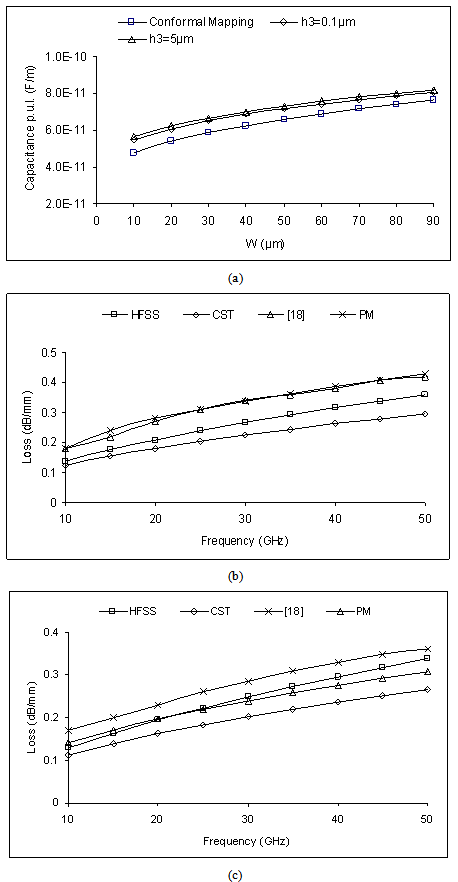
The conventional CPW consist of centred conductor between two infinite ground planes with all on the same plane. The height of substrate is also infinite. But in practical case, both the width of the ground planes and height of substrate are finite. The cross section structure of shielded multilayer coplanar waveguide of finite conductor thickness under investigation using the quasi-static SDA formulation is shown in Figure. 1.

In this paper an efficient method for calculating the line capacitance of shielded multilayer CPW of finite conductor thickness is presented. The effect of conductor thickness is accounted by accommodating the two layer strip conductor model that is suggested for a microstrip line[4]. The potential and charge distribution basis function on the strips is required to compute the line capacitance. The potential on the strips is expressed in terms of charge distribution on the upper and lower strips. The unknown charge distribution function can be expanded in term of linear combination of basis function. The total potential in the range[0, L] is equal to the sum of the potential on strips conductor and potential in two slot region. Then, Galerkin method is applied to find the unknown coefficient of chare density basis function. The total charge on the coplanar waveguide is sum of charge at upper and lower strip of centre conductor. Therefore, quasi-static SDA obtains the total charge on the central strip. By using the total charge on the central strip the per unit length capacitance is computed. The effective dielectric constant and characteristic impedance of the CPW transmission line can be determined using capacitance per unit length.

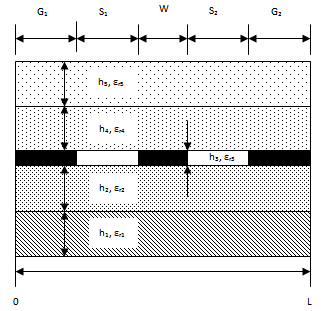Figure 1. Multilayer Shielded Coplanar Waveguide

The charge density basis functions are confined only on conductors strip and are zero outside the conductor strips. The basis function for the charge for centre strip W, left ground G₁ and right ground G₂ strip is ρ_s1i(x), ρ_s2i(x), ρ_s3i(x) respectively, where the number of basis terms of the corresponding strips. The Fourier transform of these basis functions of charge density on central conductor of width , left ground G₁ and right ground G₂ are 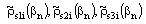respectively. In the spectral domain, the charge density basis function for lower and upper surface of conductor plane is given by-

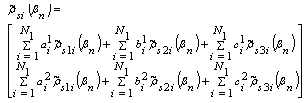(1)

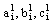where, and 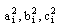are unknown constant coefficients associated with central conductor, left ground and right ground respectively for lower and upper surface of the conductor, 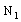is number of basis function. The Green’s function and the basis function in Fourier domain are related to potential on strip and slot region by following expression,

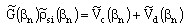(2)

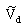where is potential on dielectric slot region and 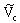is the potential on conductor strip region. The potential at lower and upper surface of the conductor are 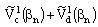and 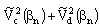respectively.

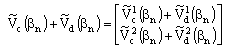(3)

The Green’s function for multilayer CPW in Fourier domain is obtained by transverse transmission line (TTL) technique. The Green’s function for the multilayer CPW shown in Figure 1 is given by

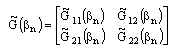(4)

where

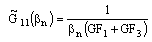(5a)

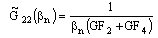(5b)

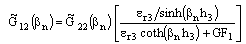(5c)

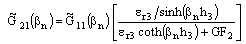(5d)

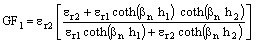(5e)

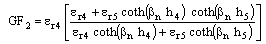(5f)

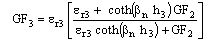(5g)

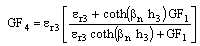(5h)

On substituting Eq.(1), Eq.(3) and Eq.(4) in Eq.(2),

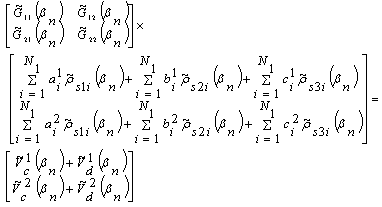(6)

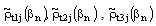Now take the inner product of Eq. (6) with testing function and applying the Parseval’s identity. By Galerkin’s method solve for the unknown constant of the charge basis function The line capacitance per unit length of finite conductor thickness CPW is computed by substituting the constants in Eq. (7).

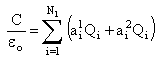(7)

where

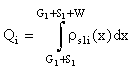The following charge distribution basis function on central and ground conductor strip is used[14].

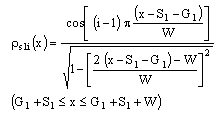(8a)

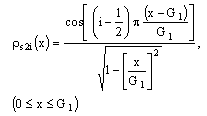(8b)

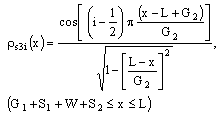(8c)

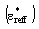The characteristic impedance (Z*) and effective dielectric constant of CPW are computed from the line capacitance of the structure filled with dielectric 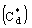and air 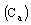from the following equations,

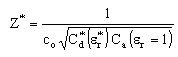(9)

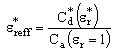(10)

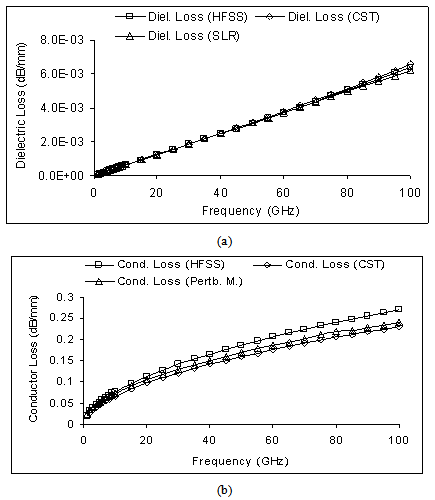
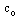where is the velocity of light in free space.

Dielectric loss of multilayer CPW is calculated by converting multilayer CPW structure into equivalent single layer CPW structure using SLR method. The complex effective relative permittivity is computed by -

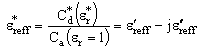(11)

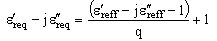(12)

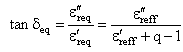(13)

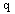where is filling factor for coplanar waveguide. The dielectric loss[15] of the coplanar waveguide is given by,

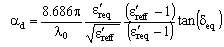(14)

The conductor loss of CPW is computed by perturbation method (Pertb. M.),[16-18].

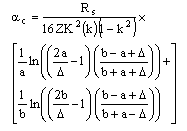(15)

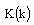where is complete elliptic integral of first kind, is stopping distance, . For symmetric configuration of CPW structure S₁=S₂=S.

where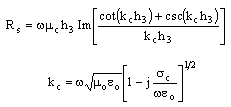

For single ground coplanar waveguide the conductor loss is computed from[9],

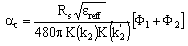(16)

where

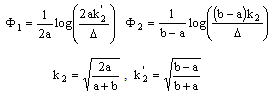
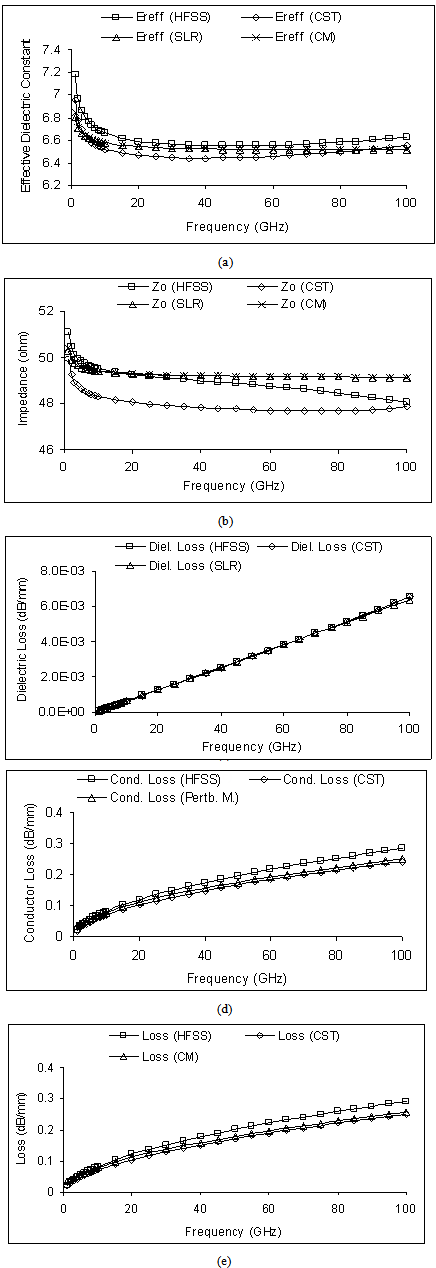
3. Dispersion Analysis of Multilayer CPW

A dispersion formula[19] for effective dielectric constant has been proposed for coplanar waveguide

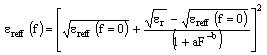(17)

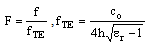whereis the cutoff frequency of the mode,

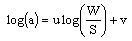(18a)

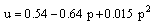(18b)

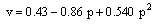(18c)

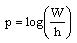(18d)

This dispersion formula was obtained under the assumption of infinitely thin conductors and infinity conductivity. To account the dispersion at low frequency an approximation for computation of increased inductance due to skin effect in strip conductor is used here. At the lower end of RF and microwave, the finite conductivity of a strip permits penetration of magnetic field inside the conductor, causing increase in effective relative permittivity and impedance with decrease in operating frequency. The penetration of the magnetic field in a conducting strip increases the effective permeability of the CPW. The effective permeability, expressed by a factor K, is computed on the air-substrate CPW by the following expression in term of capacitance. At lower frequency, we have K>>1 and at higher frequency. 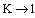As the frequency decreases, the field penetration inside the conductor increases and effective relative permittivity increases at low frequency.

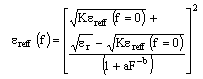(19)

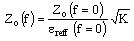(20)

where

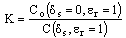
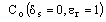is the capacitance without skin effect and 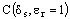is capacitance with skin effect on air substrate of CPW transmission line.

4. Circuit Model of CPW

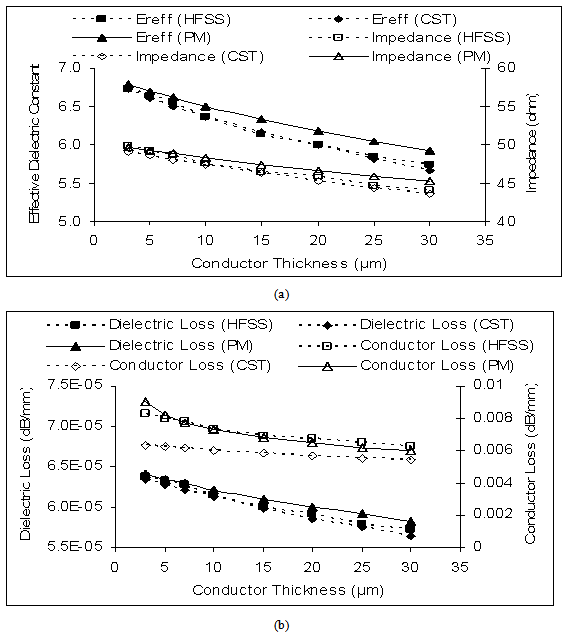
The primary line constants of a multilayer coplanar waveguide are resistance (R), conductance (G), capacitance (C) and inductance (L). These parameters are computed from the conductor loss, dielectric loss, real part of effective relative permittivity and impedance. high dielectric constant disappears at high frequency.

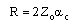(20a)

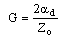(20b)

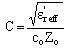(20c)

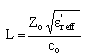(20d)

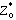The circuit model can calculate the complex characteristic impedance, phase constant and total loss of the structure. The complex characteristic impedance ( ) and complex propagation constant (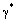) is given by,

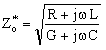(21a)

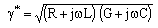(21b)

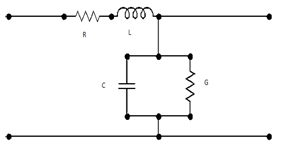Figure 2. Circuit Model of Coplanar Waveguide

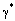The total loss is αT = Re() Np per unit length, the phase constant is β = Im(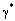) radian per unit length. The effective dielectric constant is calculated from the following relation, 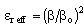, where βo is free-space phase constant.

5. Result and Discussion

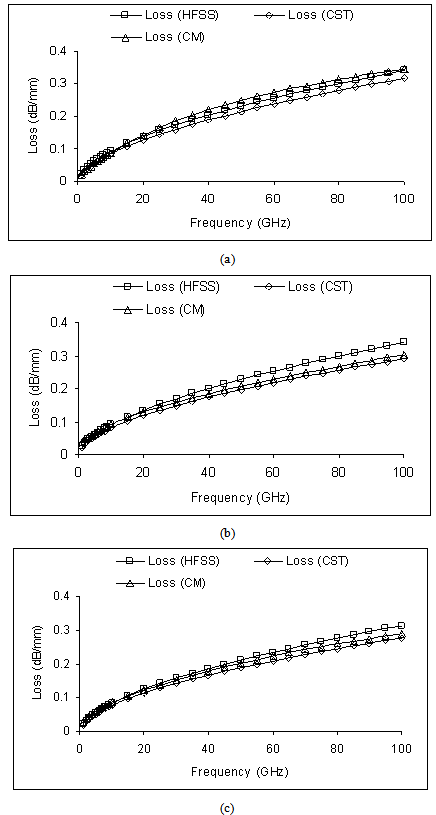
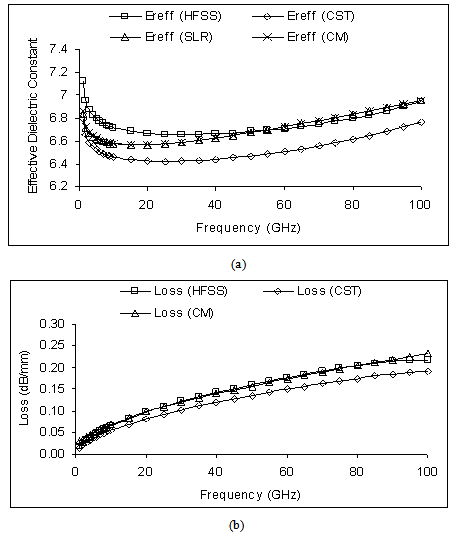
In this section, first we have validated the static SDA formulation that include two layer conductor thickness model against EM simulator- Ansoft High Frequency Structure Simulator (HFSS)[20] and Computer Simulation Technology (CST) microwave studio[21].

Figure 3. (a) Variation of Capacitance p.u.l. of CPW with the width of central conductor S1=50μm, S2=50μm, h1=500μm, h2=5μm, h4→∞, εr1=3.78, εr2=12.9, εr4=1.0. Loss versus frequency of coplanar waveguide (b) h3=1.5 µm, (c) h3=3.0 µm, h1→∞, h2=600 µm, h4=0, h5→∞, εr1=1, εr2=12.9, εr5=1, tanδ2=0.0003, W=10 µm, S1=20 µm, σ = 3.0x107 S/m.

Next we validated the frequency dependent, i.e., dynamic line parameters at low frequency obtained from the present model (PM) against the result from HFSS and CST. In Figure 3(a) the capacitance per unit length (p.u.l.) of CPW is compared with conformal mapping method. In Figure 3(b)-(c) the loss of CPW are compared against the HFSS, CST present model (PM) and[18] for different conductor thickness. Figure 4(a) show the effects of conductor thickness on effective dielectric constant and impedance for multilayer CPW. The effective dielectric constant and impedance decreases with increase of conductor thickness. In our study HFSS is taken as reference. The simulation is carried at 1 Ghz to compute ε_eff(f=0), Z(f=0) and dielectric loss. For these computations, the strip conductor is treated as a perfect conductor. The finite conductivity is considered for computation of frequency dependent line parameters. The variation in line parameters are shown with respect to conductor thickness between 3μm-30μm. The average deviation in effective dielectric constant of present model and CST with HFSS are 2.21% and 0.47% respectively.

Figure 4. Variation of (a) Effective dielectric constant and impedance (b) dielectric and conductor loss with conductor thickness of CPW h1=254µm, (b) h2=254 µm, h4=0 µm, h5=10H, εr1=9.8, εr2=12.9, εr5=1, tanδ1=0.0001, tanδ2=0.0003, W=120µm, S1=90µm, σ = 4.1x107 S/m, H= h1+ h2

The average deviation in impedance of present model and CST with HFSS are 1.35% and 0.96% respectively. Figure (4b) shows the effects of conductor thickness on dielectric loss and conductor loss. The average deviations in conductor loss of present model and CST with HFSS are 3.35% and 17.77% respectively. The average deviations in dielectric loss of present model and CST with HFSS are 1.17% and 0.67% respectively. Figure 5(a)-(e) shows variation of effective dielectric constant, impedance, dielectric loss and conductor loss for multilayer CPW with frequency.

Figure 5. Propagation characteristics of coplanar waveguide (a) effective dielectric constant (b) impedance (c) dielectric loss (d) conductor loss (e) Total Loss, h1=127 µm, h2=254 µm, h3=3 µm, h4=0, h5=10H, εr1=9.8, εr2=12.9, εr5=1, tanδ1=0.0001, tanδ2=0.0003, W=24 µm, S1=18 µm, σ = 4.1x107 S/m

The results are further improved on using the circuit model (CM). In Figure 6(a)-(b) the dielectric loss and conductor loss of multilayer CPW are compared for 1-100 GHz.

The SLR method has been used to compute the frequency dependent effective dielectric constant, impedance, dielectric loss and conductor loss. Figure 7(a)-(c) show the variation of attenuation constant of multilayer CPW for different conductor thickness by circuit model. Figure 8(a)-(b) show the variation of effective dielectric constant and loss of multilayer micro coplanar strip (MCS) with frequency.

The shielded multilayer CPW structure shown in Figure 1 can be converted into other structures such as dielectric covered CPW, suspended CPW, elevated CPW, top shield without conductor back etc. The dispersion in effective dielectric constant of CPW at low frequency due to finite conductivity of strip conductor is also incorporated. As the frequency decreases, the effective relative permittivity increases due to skin effect in conductor. The impedance of CPW line also shows the similar behaviour at low frequency region. It is clearly seen that good agreement exists between present model and EM simulator.

Figure 6. Losses of coplanar waveguide (a) dielectric loss (b) conductor loss, h1=127 µm, h2=254 µm, h3=5 µm, h4=0, h5=10H, εr1=9.8, εr2=12.9, εr5=1, tanδ1=0.0001, tanδ2=0.0003, W=24 µm, S1=18 µm, σ = 4.1x107 S/m

Figure 7. Attenuation constant of coplanar waveguide with frequency from circuit model (a) h3=1 µm (b) h3=3 µm (c) h3=5 µm, h1=127 µm, h2=254 µm, h4=0, h5=10H, εr1=3.78, εr2=9.6, εr5=1, tanδ1=0.0001, tanδ2=0.0003, W=24 µm, S1=18 µm

Figure 8. Multilayer micro coplanar strip (MCS) (a) effective dielectric constant (b) loss, h1=127 µm, h2=254 µm, h3=3 µm, h4=0, h5=10H, εr1=9.8, εr2=12.9, εr5=1, tanδ1=0.0001, tanδ2=0.0003, W=24 µm, S1=18 µm, σ = 4.1x107 S/m

6. Conclusions

In this paper, computationally efficient quasi-static SDA is used to study the effect of conductor thickness on effective dielectric constant, impedance, dielectric loss and conductor loss of shielded multilayer CPW on isotropic layered media. The accuracy of the method is investigated through the comparison between results obtained using quasi-static SDA, Ansoft HFSS, CST software and the agreement is very good. The SDA formulation incorporates the two layer model of conductor thickness and concept of permeability due to field penetration in the imperfect conductor. This formulation accounts for the effect of conductor thickness and low frequency dispersion on computation of quasi-static effective relative permittivity and characteristic impedance. The models accuracy is comparable to the accuracy of HFSS and CST, without using complex and time consuming full wave methods. The present formulation can be incorporated in the CAD of CPW based circuits and other planar transmission line with finite conductor thickness conveniently.