-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Electromagnetics and Applications
p-ISSN: 2168-5037 e-ISSN: 2168-5045
2012; 2(6): 169-173
doi: 10.5923/j.ijea.20120206.06
Genetic Algorithm Optimization of Log-Periodic Dipole Array
M. Touseef 1, Qamar -ud-Din 2, M. Aziz-ul-Haq 1, Umair Rafique 1, M. Arif Khan 1, M. Mansoor Ahmed 1
1Department of Electronic Engineering, Mohammad Ali Jinnah University, Islamabad, 44000, Pakistan
2Department of Electrical Engineering, University of Faisalabad, Faisalabad, 38000, Pakistan
Correspondence to: M. Touseef , Department of Electronic Engineering, Mohammad Ali Jinnah University, Islamabad, 44000, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper presents Genetic Algorithm (GA) optimization of Log-Periodic Dipole Array (LPDA). Considering the fact that, an LPDA can effectively be used for different wireless communication systems such as WiMAX, GSM-I, GSM-II and WiFi, respectively. GA optimization is applied to the physical size of the antenna and on its gain. The proposed design is compared with the conventional LPDA design in terms of length, diameter and spacing between the dipole elements. Presented results show that, the proposed optimization approach can significantly improve the antenna gain and reduced its size. The size of the antenna is reduced up to 12% as compared to the conventional design. Also, the gain is improved from 9.1, 9.5, 9.2 and 8.5 dB to 10.7, 11.2, 9.9 and 9.1 dB for the desired communication bands. The reduction in size and increment in gain make LPDA an attractive choice for wireless applications.
Keywords: Genetic Algorithm (GA), Log-Periodic Dipole Array (LPDA), Size Reduction, Cost Effective
Cite this paper: M. Touseef , Qamar -ud-Din , M. Aziz-ul-Haq , Umair Rafique , M. Arif Khan , M. Mansoor Ahmed , "Genetic Algorithm Optimization of Log-Periodic Dipole Array", International Journal of Electromagnetics and Applications, Vol. 2 No. 6, 2012, pp. 169-173. doi: 10.5923/j.ijea.20120206.06.
Article Outline
1. Introduction
- An antenna is a key component in any wireless communication system. These days, many wireless applications require high data rate at one hand, while small size of antenna on another hand. For this purpose, it is necessary to design such kind of antenna which is very efficient in terms of gain and occupy small space in the system. The goal of small size and high gain can be obtained using some optimization techniques such as Genetic Algorithm (GA)[1], Particle Swarm Optimization (PSO)[2] and its variants, e.g., Quantum PSO[3-6].For broadband wireless applications, Log Periodic Dipole Array (LPDA) has been used since 1960s. The first LPDA design was introduced by[7-8] which later on had different designs for different applications. In general, an LPDA is a directional antenna which possesses constant electrical characteristics such as gain, impedance and front-to-back ratio over the wide range of frequencies compared to other directional antennas. The main advantage of an LPDA is that, it is essentially a frequency independent antenna for a certain multi-band communication system[9]. This paper presents the design of an LPDA which can operate at WiMAX, GSM-I, GSM-II and WiFi wireless communication bands. The main objective is to optimize the design using Genetic Algorithm (GA). However, there are other research works where GA is used to optimize different kind of antennas[1],[10-15]. In[1], authors used GA to find efficient new resonant wire antenna that perform best within the volume they are confined. In[10], authors used GA and Method of Moment (MoM) to compress the size of an LPDA in terms of its number of elements. However, in this work, we have optimized the overall size of the antenna. In[11], authors optimized an LPDA using GA, Nelder-Mead simplex algorithm and a combination of both algorithms. The optimization problem presented in this paper has two objective functions. The design procedure is as follows: (1) First step is to design an LPDA using conventional technique and then analyse the response in terms of gain; (2) in the second step, we applied GA algorithm to optimize the antenna. The results of conventional design and the optimized design are discussed in Section 4.The remainder of the paper is organized as follows. Section 2 explains the basics of Genetic Algorithm (GA). Section 3 discusses the design and optimization of an LPDA. Section 4 presents the results and discussion on results. Finally, we concluded the paper in Section 5.
2. Genetic Algorithm (GA)
- Genetic Algorithm is based on the principle of best gene selection from a huge available population of genes. A portion of the worst population is rejected and the remaining population is arranged in a particular order. Two random selected best genes from the remaining population are allow- -ed to mate and create a new population. After certain number of iterations, the available population, in general, is the best population[16-17]. This principle of Genetic Algorithm is applied by different researchers on the antenna design[10-15].Genes are the basic building blocks in any Genetic Algorithm technique. A gene is a binary encoding of a design parameters. Basically, chromosome is an array of genes. The chromosomes are evaluated by a function called cost function. The chromosomes are ranked from the most-fit to the least-fit and unacceptable chromosomes are discarded from the lower rank. Genes who survives become parents and by swapping some of their genetic material, new offspring is produced. The parents reproduce enough chromosomes to offset the discarded chromosomes. Thus, the total number of chromosomes remains constant in each iteration. The complete flow diagram of Genetic Algorithm is shown in Fig. 1.
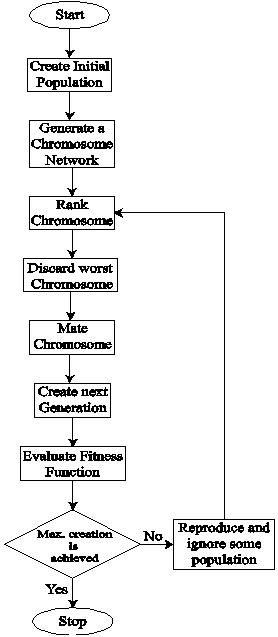 | Figure 1. Flow diagram of Genetic Algorithm |
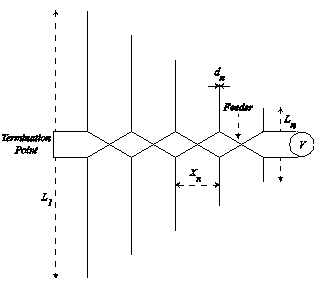 | Figure 2. Geometry of Log Periodic Dipole Array |
3. Design and Optimization of an LPDA
- A typical LPDA consists of a number of dipole elements Li where, i = 1, … , n showing that L1 and Ln are the largest and smallest elements mounted on a common feed network. The length, diameter and spacing of each element is different from the other elements. The schematic diagram of an LPDA is shown in Fig. 2. The smallest dipole element Ln is fed with a sinusoidal current of form i(t) = Asin(ωt) where, maximum value of i(t) is assumed to be unity. The step by step procedure of an LPDA is described in[18-20]. The basic design equations used to determine LPDA parameters are given below:
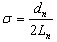 | (1) |
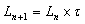 | (2) |
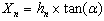 | (3) |
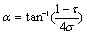 | (4) |
3.1. Implementation of GA
- The first step in the algorithm implementation is to create a random population which consists of LPDA parameters such as length, diameter and spacing of each dipole element. In next step, we define a chromosome vector C which comprises of length (10 length genes), diameter (10 diameter genes) and spacing between two consecutive elements (9 spacing genes), respectively. Eq. (5) shows the chromosome vector C. Our task is to optimize the define parameters in the chromosome vector.
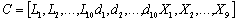 | (5) |
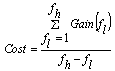 | (6) |
4. Results and Discussion
- This section presents the results of the proposed LPDA design. The main objective was to optimize an LPDA in such a way that, it works well in the desired frequency bands with the acceptable parameters which are physical size of an LPDA and its gain. The initial response is obtained by evaluating the design parameters and writing a MATLAB routine. The initial gain for different communication bands is shown in Fig. 3-6. After that, GA optimization is applied to the design parameters and the improvement in the gain is demonstrated. The results for the optimized design are shown in Fig. 3-6. These results show considerable improvement as compared to the conventional design. The gain is improved up to 85% for WiMAX band, approximately 85% for GSM-I, 93% for GSM-II and 93.5% for WiFi band, respectively. It is demonstrated that the proposed algorithm results are approximately similar to the previously presented work[2]. The major improvement in gain is noticed for WiMAX, GSM-I and GSM-II frequency bands as compared to the previous work[2]. The comparison of previous work with the proposed work is shown in Fig. 3-6. Also, the difference noticed in the computational time that, Genetic Algorithm (GA) optimization took less time to evaluate the parameters as compared to the Particle Swarm Optimization (PSO) and Quantum Particle Swarm Optimization (QPSO).
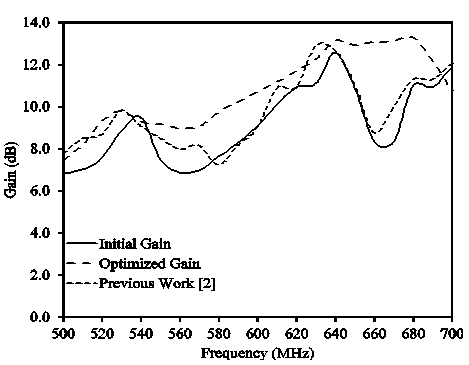 | Figure 3. Initial and optimized gain for WiMAX |
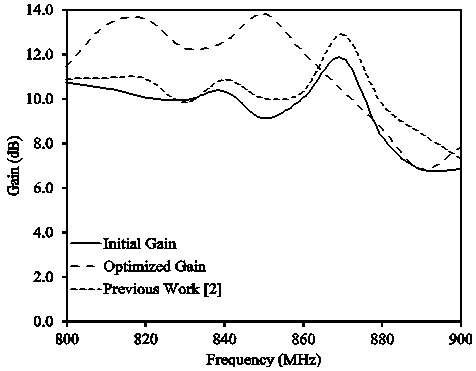 | Figure 4. Initial and optimized gain for GSM-I |
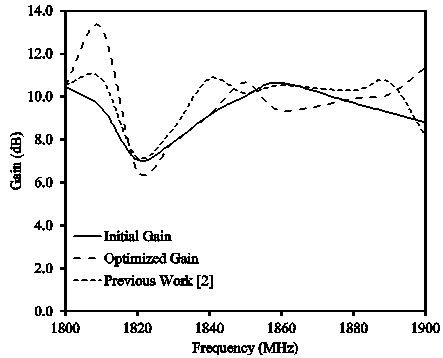 | Figure 5. Initial and optimized gain for GSM-II |
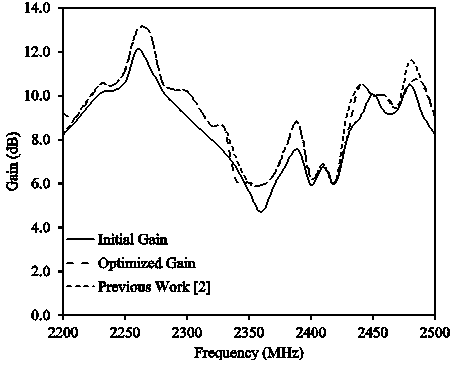 | Figure 6. Initial and optimized gain for WiFi |
5. Conclusions
- The Log Periodic Dipole Array (LPDA) is designed for WiMAX, GSM-I, GSM-II and WiFi communication bands. Antenna parameters are optimized by using Genetic Algorithm (GA). The initial calculated average gain for each communication band is 9.1 dB, 9.5 dB, 9.2 dB and 8.5 dB, respectively. However, the optimum solution of average gain is 10.7 dB, 11.2 dB, 9.9 dB and 9.1 dB, respectively. It is also observed that the reduction occurred in the antenna size is 12% as compared to the initial design. With smaller size and high gain, the proposed design is an attractive choice for many wireless applications.
References
| [1] | Altshuler, E. E., “Electrically small self-resonant wire antennas optimized using genetic algorithm”, IEEE Transactions on Antennas and Propagation, vol. 50, no. 3, pp. 297-300, 2002. |
| [2] | Haq, M. A., Rana, M. T., Rafique, U., Memon, Q.D., Khan, M. A. and Ahmed, M. M., “Log periodic dipole antenna design using particle swarm optimization”, International Journal of Electromagnetics and Applications (IJEC), vol. 2, no. 4, pp. 65-68, 2012. |
| [3] | Wang, T., Wang, S., Zhang, W. and Zhang, Z., “Pattern synthesis of array antennas with a kind of quantum particle swarm optimization”, Advances in Intelligent and Soft Computing, vol. 129, pp. 123-130, 2011. |
| [4] | Mikki, S. M. and Kishk, A. A., “Investigation of the quantum particle swarm optimization technique for electromagnetic applications”, 2005 IEEE Antennas and Propagation Society International Symposium, vol. 2A, pp. 45-48, 2005. |
| [5] | Mikki, S. M. and Kishk, A. A., “Quantum particle swarm optimization for electromagnetics”, IEEE Transactions on Antennas and Propagation, vol. 54, no. 10, pp. 2764-2775, 2006. |
| [6] | Mikki, S. M. and Kishk, A. A., “Theory and applications of infinitesimal dipole models for computational electromagnetics”, IEEE Transactions on Antennas and Propagation, vol. 55, no. 5, pp. 1325-1337, 2007. |
| [7] | Isbell, D., “Log periodic dipole arrays”, IRE Transactions on Antennas and Propagation, vol. 8, pp. 260-267, 1960. |
| [8] | Carrel, R., “The design of log-periodic dipole antennas”, IRE International Convention Record, vol. 9, pp. 61-75, 1961. |
| [9] | Rumsey, V. H., “Frequency independent antennas”, IRE International Convention Record, vol. 5, pp. 114-118, 1957. |
| [10] | Mangoud, M. A., Dahab, M. A. A., Zaki, A. I. and El-Khamy, S. E., “Genetic algorithm design of compressed log periodic dipole array”, IEEE 46th Midwest Symposium on Circuits and Systems, vol. 3, pp. 1194-1197, 2003. |
| [11] | Chung, Y. C. and Haupt, R., “Log-periodic dipole array optimization”, IEEE Conference on Aerospace, vol. 4, pp. 449-455, 2000. |
| [12] | Altshuler, E. E. and Linden, D. S. “Design of a loaded monopole having hemispherical coverage using genetic algorithm”, IEEE Transactions on Antennas and Propagation, vol. 45, no. 1, pp. 1-4, 1997. |
| [13] | Boag, A., Michielssen, E. and Mittra, R., “Design of electrically loaded wire antennas using genetic algorithm”, IEEE Transactions on Antennas and Propagation, vol. 44, no. 5, pp. 687-695, 1996. |
| [14] | Altman, Z., Mittra, R. and Boag, A., “New design of ultra-wideband communication antennas using a genetic algorithm”, IEEE Transactions on Antennas and Propagation, vol. 45, no. 10, pp. 1494-1501, 1997. |
| [15] | Altshuler, E. E. and Linden, D. S., “Wire antenna designs using genetic algorithm”, IEEE Antennas and Propagation Magazine, vol. 39, no. 2, pp. 33-43, 1997. |
| [16] | Holland, J. H., “Genetic algorithm and the optimal allocations of trails”, SIAM Journal of Computing, vol. 2, no. 2, pp. 88-105, 1973. |
| [17] | Sivanandam, S. N. and Deepa, S. N., Introduction to Genetic Algorithms, 2008. |
| [18] | Voti, G. D. and Staracca, G., “Comments on the design of log periodic dipole antennas”, IEEE Transactions on Antennas and Propagation, vol. 21, pp. 303-308, 1973. |
| [19] | Bantin, C. and Balmain, K., “Study of compressed log-periodic dipole antennas”, IEEE Transactions on Antennas and Propagation, vol. 18, pp. 195-203, 1970. |
| [20] | Balanis, C. A., Antenna Theory and Design, 3rd Edition. |
| [21] | Eberhart, R. and Kennedy, J., “A new optimizer using particle swarm theory”, Proceedings of the 6th International Symposium on Microwave Machine and Human Science, pp. 39-43, 1995. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML