V. A. Malakhov , A. S. Raevskii , S. B. Raevskii
Nizhniy Novgorod State Technical University, Nizhniy Novgorod, Russia
Correspondence to: V. A. Malakhov , Nizhniy Novgorod State Technical University, Nizhniy Novgorod, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Existence of the added waves in double-layered cylindrical guiding structures is considered in the article.The added waves ensure completeness of solutions of boundary value problems for layered guiding structures.It is shown that eigenvalues, corresponding added waves (or adjoint waves), can be detected at points of the Jordan’s multiplicity of the wavenumbers. At these points characteristics of two normal waves joint and complex waves originate. The added waves define frequency boundaries of a complex resonance which originates as a result of a exciting of couple of complex waves.
Keywords:
Added Waves, Adjoint Waves, Round Guiding Structures, Boundary Value Problems
1. Introduction
The question about added waves of guidingelectrodynamics structures is emerged in connection with boundary value problems: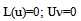 | (1) |
(L – Differentiation operator, Uν=0 – system of boundary conditions, ν=1,2,3 … n),for which we can formulate added boundary value problems, consisting of differential equations: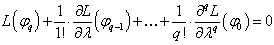 | (2) |
where q=1,2 …k, and boundary conditions: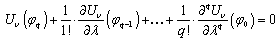 | (3) |
Functions φq in Eq. (2) and Eq. (3) are called the added (or adjoint) functions. Functions φq are added to the function φ0. These functions obey Eq. (2) and boundary conditions Eq. (3) for eigenvalues λ=λ0. φ0 – the solving of the boundary value problem (1).Solutions of the adjoined boundary value problems describe the so-called added waves or adjoint waves (AWs)[2]. In[3], it was showed that AWs origin in the points of the Jordan’s multiplicity of the wavenumbers of normal waves. AWs ensure the completeness of the system of normal waves, which are violated in these points. Completeness of system of normal waves is used for solving of diffraction problems, intended for the calculation of functional units for microwave and extremely high frequency. Completeness of diffraction basis determines correctness of solutions of the boundary value problem.Features of AWs influence characteristics of complex resonance[4-6], which originates in guiding structures (the result of pair interaction of complex waves).A steepness of front of frequency characteristic of a band-pass filter on complex resonance[7] depends on accounting of AWs. Characteristic property of AWs is linear dependence of their amplitudes from longitudinal coordinate. First particular information about results of solution of the added boundary value problems for multilayer guiding cylindrical structures was perhaps presented in[8-10].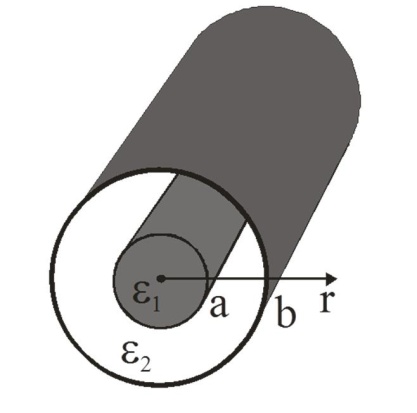 | Figure 1a. The round double-layer shielded waveguide |
2. The Boundary Value Problems for Added Waves of Double-Layer Guiding Cylindrical Structures
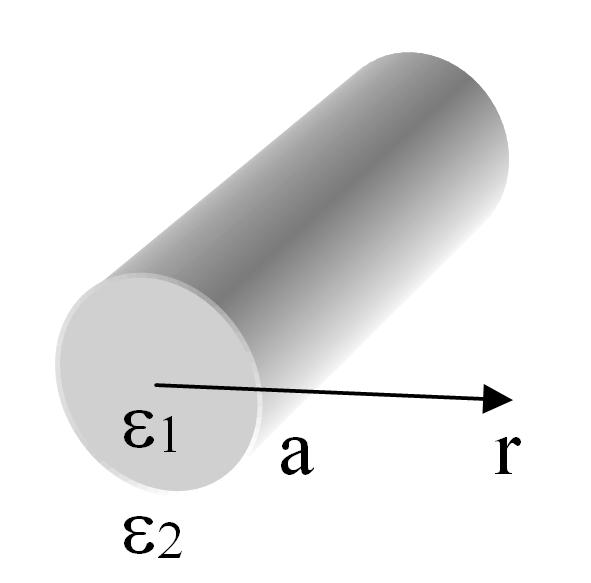
In this paper guiding cylindrical structures with two concentric layers are discussed. The article deals with a round shielded waveguide with two concentric layers (Fig. 1a) or a round dielectric waveguide placed in infinite homogeneous medium (Fig. 1b). These structures are used in functional units for microwave, extremely-high frequency and optical devices. Electromagnetic fields in these guiding structures are described by longitudinal components of the Herz vectors of electric and magnetic fields, which obey the Helmholtz equation: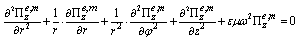 | (4) |
 | Figure 1b. The round dielectric waveguide |
where r, z are the cylindrical coordinates. A solution of this equation that corresponds to the AWs has the following form: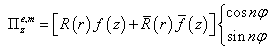 | (5) |
Functions incoming in Eq. (5) obey equations: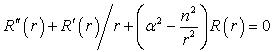 | (6) |
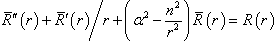 | (7) |
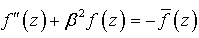 | (8) |
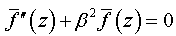 | (9) |
α and β are the transverse and longitudinal wave numbers, that are related as:  Eqs. (7) and (8) are added to Eqs (6) and (7), respectively.R(r) is either the Bessel function (for the radial field profile in the inner layer of the guiding structure) or a combination of cylindrical functions of the 1st and 2nd kind obeying the corresponding (Dirichlet or Neumann) boundary conditions on the shield (for the radial field profile in the outer layer) or the Hankel function for the field in the outer infinite layer of a round dielectric waveguide.The Herz vectors (5) are written[5] in the following form:where q = 1, 2 is the layer number
Eqs. (7) and (8) are added to Eqs (6) and (7), respectively.R(r) is either the Bessel function (for the radial field profile in the inner layer of the guiding structure) or a combination of cylindrical functions of the 1st and 2nd kind obeying the corresponding (Dirichlet or Neumann) boundary conditions on the shield (for the radial field profile in the outer layer) or the Hankel function for the field in the outer infinite layer of a round dielectric waveguide.The Herz vectors (5) are written[5] in the following form:where q = 1, 2 is the layer number 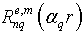 are the solutions of Eq. (6);
are the solutions of Eq. (6);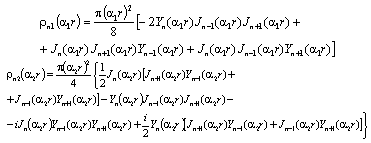 Function
Function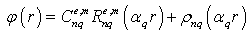 is the added general solution of Eq. (7); Jν and Yν are the cylindrical functions of the 1st and 2nd kind.Function (10) is a solution of the added Helmholtz equation. In right part of the equation is expression:
is the added general solution of Eq. (7); Jν and Yν are the cylindrical functions of the 1st and 2nd kind.Function (10) is a solution of the added Helmholtz equation. In right part of the equation is expression: Function (10) will obey the normal Helmholtz equation, if function
Function (10) will obey the normal Helmholtz equation, if function 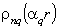 is a solution of the added Bessel equation:Using the boundary conditions formulated as we arrive at a system of equations that determine functions dependent on the longitudinal coordinate. Equating the terms linearly dependent on the longitudinal coordinate z, we obtain a system of four linear homogeneous algebraic equations with respect to coefficients
is a solution of the added Bessel equation:Using the boundary conditions formulated as we arrive at a system of equations that determine functions dependent on the longitudinal coordinate. Equating the terms linearly dependent on the longitudinal coordinate z, we obtain a system of four linear homogeneous algebraic equations with respect to coefficients  :
: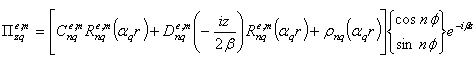 | (10) |
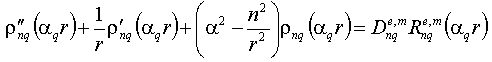 | (11) |
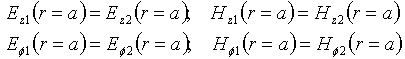 | (12) |
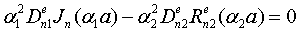 | (13a) |
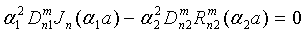 | (13b) |
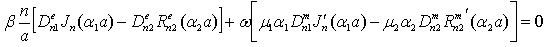 | (13c) |
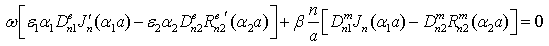 | (13d) |
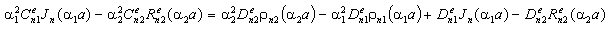 | (14a) |
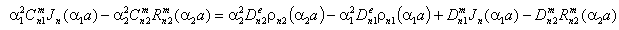 | (14b) |
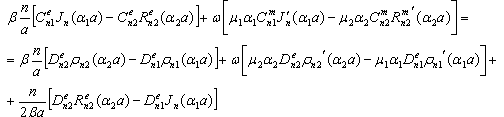 | (14c) |
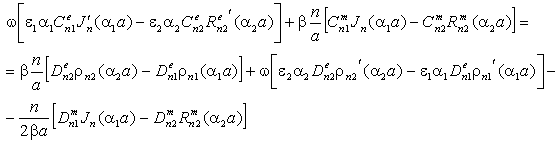 | (14d) |
Terms of these functional equations, which haven’t coordinate dependence, (fulfilment of condition (11) reduce to system of linear inhomogeneous algebraic equations with respect to coefficients :The main determinant of a system (13) coincides with the determinant of a system (14). If determinates equate zero, we will obtain dispersion characteristics of normal waves of double-layer guiding cylindrical structures such as: a round double-layer shielded waveguide and a round open dielectric waveguide.Nontrivial solutions of the system of Eqs. (13) (coefficients
:The main determinant of a system (13) coincides with the determinant of a system (14). If determinates equate zero, we will obtain dispersion characteristics of normal waves of double-layer guiding cylindrical structures such as: a round double-layer shielded waveguide and a round open dielectric waveguide.Nontrivial solutions of the system of Eqs. (13) (coefficients are substituted into the system of Eqs. (14), which is solved with respect to coefficients
are substituted into the system of Eqs. (14), which is solved with respect to coefficients 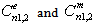 .So long as, the boundary conditions (12) must be executed, the system of Eqs. (13) and (14) must have common solutions. The system of Eqs. (13) will have got nontrivial solutions when determinant of the system is zero. As far as the main determinant of the system (14) coincides with the main determinant of the system (13), the system (14) can have got the added solutions when the additional determinants equal zero. The wavenumbers of the added waves are determined by joint solutions of three equations:First equation:
.So long as, the boundary conditions (12) must be executed, the system of Eqs. (13) and (14) must have common solutions. The system of Eqs. (13) will have got nontrivial solutions when determinant of the system is zero. As far as the main determinant of the system (14) coincides with the main determinant of the system (13), the system (14) can have got the added solutions when the additional determinants equal zero. The wavenumbers of the added waves are determined by joint solutions of three equations:First equation: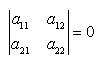 | (15) |
coinciding with dispersion equation of normal waves of double-layer guiding cylindrical structures, and two additional equations: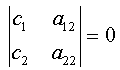 | (16a) |
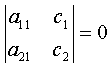 | (16b) |
where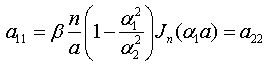
 Eqs. (15), (16a) and (16b) are solved together with equations:
Eqs. (15), (16a) and (16b) are solved together with equations: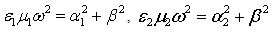 | (17) |
Solutions of the dispersion problem for AWs are represented by compatible solutions of the system of three Eqs. (15), (16a) and (16b).From boundary conditions (12), we can obtain: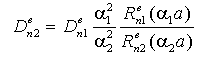 | (18a) |
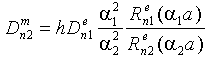 | (18b) |
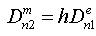 | (18c) |
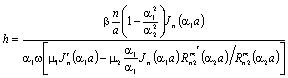 | (18d) |
Relations (18) enable to exclude coefficients 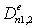 and
and  from Eqs. (16 a,b) and these equations are reduce to transcendental form.The search of wave numbers of AWs comes to compatible solutions of three transcendent Eqs. (15) and (16a,b). Wave numbers are related by Eqs. (17). From (Eq. 18), if
from Eqs. (16 a,b) and these equations are reduce to transcendental form.The search of wave numbers of AWs comes to compatible solutions of three transcendent Eqs. (15) and (16a,b). Wave numbers are related by Eqs. (17). From (Eq. 18), if  , coefficients
, coefficients 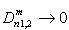 . If the condition
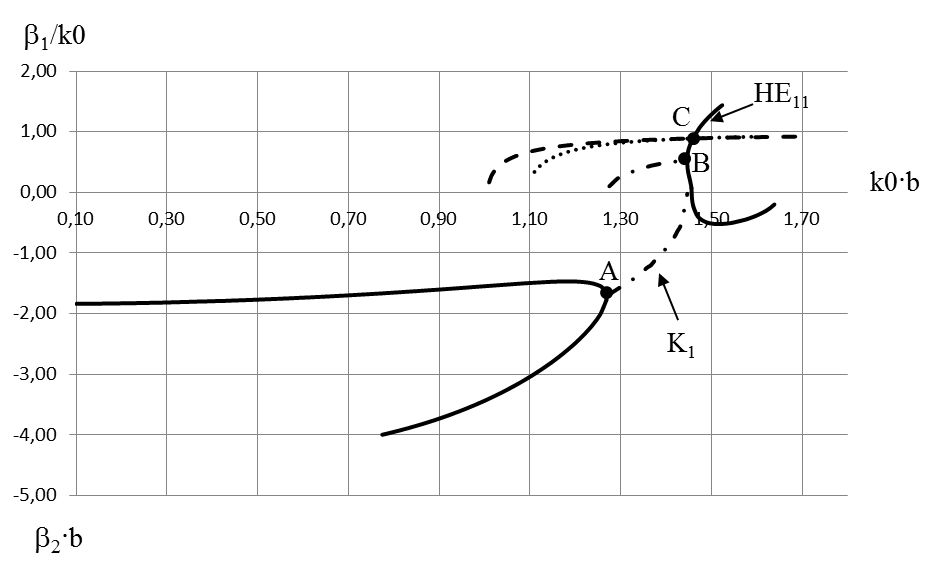
. If the condition 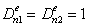 is executed, solution (10) will satisfy normal Helmholtz equation. A numerical analysis shows that this variant may be obtained. Solutions of the dispersion problem, corresponding to the AWs, are placed into the area of evanescent waves (at points of the jointing of characteristics of two normal waves, Fig. 2, point A). At this point of the Jordan’s multiplicity of the wavenumbers of normal waves the solution of the added boundary value problem is evaluated.
is executed, solution (10) will satisfy normal Helmholtz equation. A numerical analysis shows that this variant may be obtained. Solutions of the dispersion problem, corresponding to the AWs, are placed into the area of evanescent waves (at points of the jointing of characteristics of two normal waves, Fig. 2, point A). At this point of the Jordan’s multiplicity of the wavenumbers of normal waves the solution of the added boundary value problem is evaluated.
3. Numerical Solution of Dispersion Characteristics of the Added Waves of Round Double-Layer Shielded Waveguide
A compatible solution of the systems (Eqs. 15, 16a and 16b) on the complex planes of wavenumbers was obtained using a combined approach in the search for complex roots of transcendent equations. This approach represented a combination of the Muller method and the phase variation method, thus using advantages of both rapidly finding a complex root by the first method and reliably identifying this root by the second method. At the point of the jointing of characteristics of waves НЕ12 and ЕН12 (Fig. 2, point A) complex waves are appeared with the parameters of the round double-layer shielded waveguide (Fig. 1a): 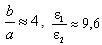 and the expression
and the expression 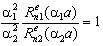 is executed. At the point wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). Compatible solutions correspond to the added waves. Coefficients
is executed. At the point wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). Compatible solutions correspond to the added waves. Coefficients 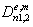 are solutions of a system of Eqs. (13), (14). With others parameters:
are solutions of a system of Eqs. (13), (14). With others parameters:  , the expression
, the expression 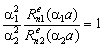 is executed too. Wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). At this points the solution (10) obeys the Helmholtz Eq. (4) and boundary conditions (12).
is executed too. Wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). At this points the solution (10) obeys the Helmholtz Eq. (4) and boundary conditions (12). 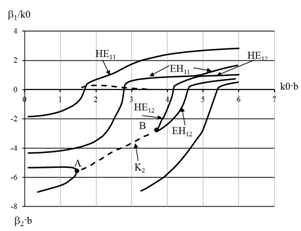 | Figure 2. Dispersion characteristics of normal waves of a round double-layer shielded waveguide, where 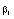 – real part and – real part and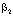 – imaginary part of the longitudinal propagation number, – imaginary part of the longitudinal propagation number, 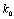 – the free-space wavenumber, b – the radius of a shield – the free-space wavenumber, b – the radius of a shield |
 | Figure 3. Solutions of Eqs. (15), (16a) and (16b) |
For arbitrary values of coefficients  solutions of three transcendental equations don’t converge at the point of a formation of complex waves (points A and B), they converge at arbitrary points of dispersion characteristics of normal waves (Fig. 3, point C). Fig. 3 shows a numerical solution of Eq. (15) (solid curve), Eq. (16a) (dashed curve), and Eq. (16b) (dotted curve) with
solutions of three transcendental equations don’t converge at the point of a formation of complex waves (points A and B), they converge at arbitrary points of dispersion characteristics of normal waves (Fig. 3, point C). Fig. 3 shows a numerical solution of Eq. (15) (solid curve), Eq. (16a) (dashed curve), and Eq. (16b) (dotted curve) with 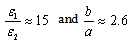 . Complex wave is showed by chain curve. Fig. 4 is an oversize.
. Complex wave is showed by chain curve. Fig. 4 is an oversize.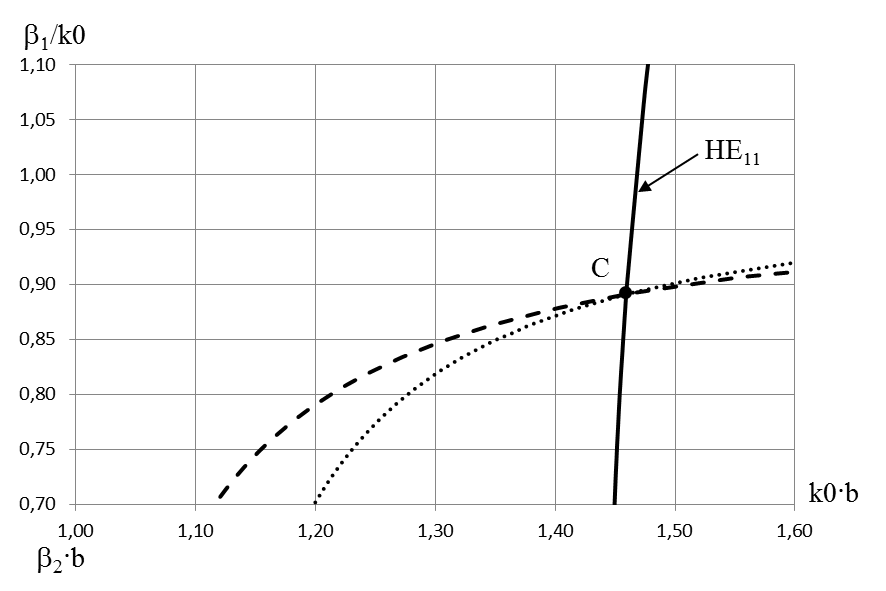 | Figure 4. Solutions of Eqs. (15), (16a) and (16b) (It is an oversize) |
4. Conclusions
It is shown that multiple eigenvalues of boundary value problems can exist. The multiplicity of eigenvalues shows a possibility of a existence waves which have different features (different longitudinal dependences of field).The AWs are characterized by a linear dependence of the field on the longitudinal coordinate. The AWs must be taken into consideration for a calculating and a constructing of components, which use the effect of the complex resonance.We have showed that two kinds of solutions of added boundary value problems can be. The first solution is only at points of the Jordan’s multiplicity of the wavenumbers of normal waves. Second solution is at points of curve crossings of solutions of three transcendent equations which are obtained from the condition of an existence of solutions of a system of algebraic equations. Second solution of added boundary value problem is calculated for any parameters of guiding cylindrical structures.
References
| [1] | M. A. Naimark, Linear Differential Equations (Nauka, Moscow, 1969)[in Russian]. |
| [2] | A.S. Il’inskii and G. Ya. Slepyan, Oscillations and Waves in Lossy Electrodynamic Systems (Izdat. MGU, Moscow, 1983)[in Russian]. |
| [3] | P. E. Krasnushkin and E. N. Fedorov, Radiotekhn. Elektron. Vol. 17, No 6, p. 1129 (1972). |
| [4] | G. I. Veselov and S. B. Raevskii, Layered Metal–Dielectric Waveguides (Radio i Svyaz’, Moscow, 1988)[in Russian]. |
| [5] | A.E. Ivanov, S.B. Raevskii, Radiotekhn. Elektron. Vol. 36, No8, p. 1463 (1991). |
| [6] | A. S. Raevskii and S. B. Raevskii, Complex Waves (Radiotekhnika, Moscow, 2010)[in Russian]. |
| [7] | G. I. Veselov, V.A. Kalmyk and S. B. Raevskii, Izv. Vyssh. Uchebn. Zaved., Radiofiz., Vol. 26, No 8. p. 900 (1983). |
| [8] | V.A. Malakhov, A. S. Raevskii and S. B. Raevskii, The physics and technology applications of wave processes, Vol. 13, No 3 (2010). |
| [9] | V.A. Malakhov, A. S. Raevskii and S. B. Raevskii, Antennas, No 12, p. 44 (2010) |
| [10] | V.A. Malakhov, A. S. Raevskii and S. B. Raevskii, Technical physics letters, Vol. 37 No. 1(2011) |
| [11] | S. B. Raevskii, Izv. Vyssh. Uchebn. Zaved., Radiofiz., Vol. 15, No 1. p. 112 (1972). |
| [12] | S. B. Raevskii, Izv. Vyssh. Uchebn. Zaved., Radiofiz., Vol. 15, No 12. p. 1926 (1972). |

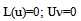
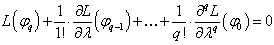
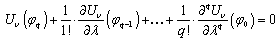

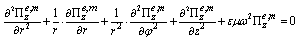

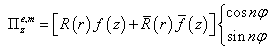
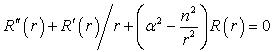
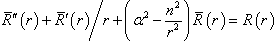
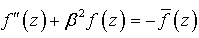
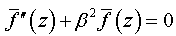
 Eqs. (7) and (8) are added to Eqs (6) and (7), respectively.R(r) is either the Bessel function (for the radial field profile in the inner layer of the guiding structure) or a combination of cylindrical functions of the 1st and 2nd kind obeying the corresponding (Dirichlet or Neumann) boundary conditions on the shield (for the radial field profile in the outer layer) or the Hankel function for the field in the outer infinite layer of a round dielectric waveguide.The Herz vectors (5) are written[5] in the following form:where q = 1, 2 is the layer number
Eqs. (7) and (8) are added to Eqs (6) and (7), respectively.R(r) is either the Bessel function (for the radial field profile in the inner layer of the guiding structure) or a combination of cylindrical functions of the 1st and 2nd kind obeying the corresponding (Dirichlet or Neumann) boundary conditions on the shield (for the radial field profile in the outer layer) or the Hankel function for the field in the outer infinite layer of a round dielectric waveguide.The Herz vectors (5) are written[5] in the following form:where q = 1, 2 is the layer number  are the solutions of Eq. (6);
are the solutions of Eq. (6);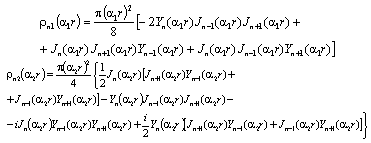 Function
Function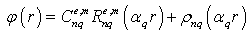 is the added general solution of Eq. (7); Jν and Yν are the cylindrical functions of the 1st and 2nd kind.Function (10) is a solution of the added Helmholtz equation. In right part of the equation is expression:
is the added general solution of Eq. (7); Jν and Yν are the cylindrical functions of the 1st and 2nd kind.Function (10) is a solution of the added Helmholtz equation. In right part of the equation is expression: Function (10) will obey the normal Helmholtz equation, if function
Function (10) will obey the normal Helmholtz equation, if function 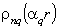 is a solution of the added Bessel equation:Using the boundary conditions formulated as we arrive at a system of equations that determine functions dependent on the longitudinal coordinate. Equating the terms linearly dependent on the longitudinal coordinate z, we obtain a system of four linear homogeneous algebraic equations with respect to coefficients
is a solution of the added Bessel equation:Using the boundary conditions formulated as we arrive at a system of equations that determine functions dependent on the longitudinal coordinate. Equating the terms linearly dependent on the longitudinal coordinate z, we obtain a system of four linear homogeneous algebraic equations with respect to coefficients  :
: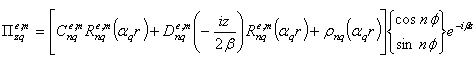
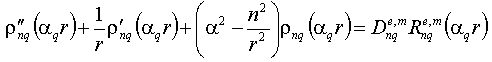
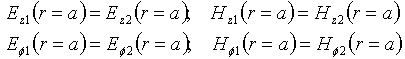
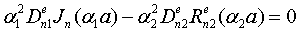
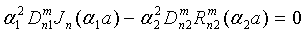
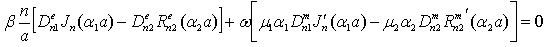
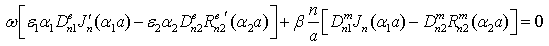
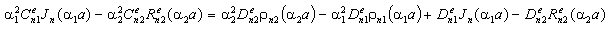
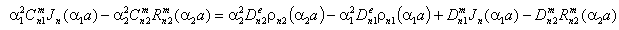
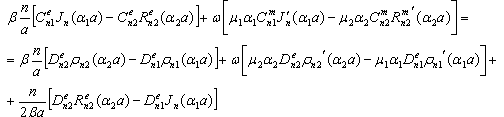
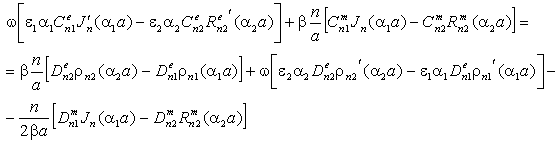
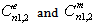 :The main determinant of a system (13) coincides with the determinant of a system (14). If determinates equate zero, we will obtain dispersion characteristics of normal waves of double-layer guiding cylindrical structures such as: a round double-layer shielded waveguide and a round open dielectric waveguide.Nontrivial solutions of the system of Eqs. (13) (coefficients
:The main determinant of a system (13) coincides with the determinant of a system (14). If determinates equate zero, we will obtain dispersion characteristics of normal waves of double-layer guiding cylindrical structures such as: a round double-layer shielded waveguide and a round open dielectric waveguide.Nontrivial solutions of the system of Eqs. (13) (coefficients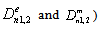 are substituted into the system of Eqs. (14), which is solved with respect to coefficients
are substituted into the system of Eqs. (14), which is solved with respect to coefficients 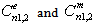 .So long as, the boundary conditions (12) must be executed, the system of Eqs. (13) and (14) must have common solutions. The system of Eqs. (13) will have got nontrivial solutions when determinant of the system is zero. As far as the main determinant of the system (14) coincides with the main determinant of the system (13), the system (14) can have got the added solutions when the additional determinants equal zero. The wavenumbers of the added waves are determined by joint solutions of three equations:First equation:
.So long as, the boundary conditions (12) must be executed, the system of Eqs. (13) and (14) must have common solutions. The system of Eqs. (13) will have got nontrivial solutions when determinant of the system is zero. As far as the main determinant of the system (14) coincides with the main determinant of the system (13), the system (14) can have got the added solutions when the additional determinants equal zero. The wavenumbers of the added waves are determined by joint solutions of three equations:First equation: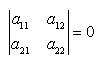
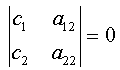
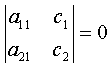
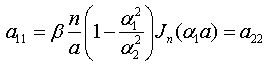
 Eqs. (15), (16a) and (16b) are solved together with equations:
Eqs. (15), (16a) and (16b) are solved together with equations: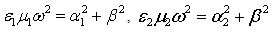
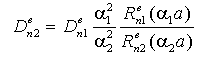
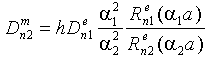
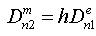
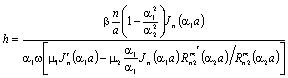
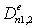 and
and  from Eqs. (16 a,b) and these equations are reduce to transcendental form.The search of wave numbers of AWs comes to compatible solutions of three transcendent Eqs. (15) and (16a,b). Wave numbers are related by Eqs. (17). From (Eq. 18), if
from Eqs. (16 a,b) and these equations are reduce to transcendental form.The search of wave numbers of AWs comes to compatible solutions of three transcendent Eqs. (15) and (16a,b). Wave numbers are related by Eqs. (17). From (Eq. 18), if  , coefficients
, coefficients 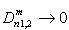 . If the condition
. If the condition 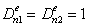 is executed, solution (10) will satisfy normal Helmholtz equation. A numerical analysis shows that this variant may be obtained. Solutions of the dispersion problem, corresponding to the AWs, are placed into the area of evanescent waves (at points of the jointing of characteristics of two normal waves, Fig. 2, point A). At this point of the Jordan’s multiplicity of the wavenumbers of normal waves the solution of the added boundary value problem is evaluated.
is executed, solution (10) will satisfy normal Helmholtz equation. A numerical analysis shows that this variant may be obtained. Solutions of the dispersion problem, corresponding to the AWs, are placed into the area of evanescent waves (at points of the jointing of characteristics of two normal waves, Fig. 2, point A). At this point of the Jordan’s multiplicity of the wavenumbers of normal waves the solution of the added boundary value problem is evaluated.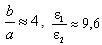 and the expression
and the expression 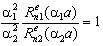 is executed. At the point wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). Compatible solutions correspond to the added waves. Coefficients
is executed. At the point wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). Compatible solutions correspond to the added waves. Coefficients 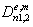 are solutions of a system of Eqs. (13), (14). With others parameters:
are solutions of a system of Eqs. (13), (14). With others parameters:  , the expression
, the expression 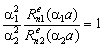 is executed too. Wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). At this points the solution (10) obeys the Helmholtz Eq. (4) and boundary conditions (12).
is executed too. Wave numbers are a compatible solution of three Eqs. (15), (16a) and (16b). At this points the solution (10) obeys the Helmholtz Eq. (4) and boundary conditions (12). 
 solutions of three transcendental equations don’t converge at the point of a formation of complex waves (points A and B), they converge at arbitrary points of dispersion characteristics of normal waves (Fig. 3, point C). Fig. 3 shows a numerical solution of Eq. (15) (solid curve), Eq. (16a) (dashed curve), and Eq. (16b) (dotted curve) with
solutions of three transcendental equations don’t converge at the point of a formation of complex waves (points A and B), they converge at arbitrary points of dispersion characteristics of normal waves (Fig. 3, point C). Fig. 3 shows a numerical solution of Eq. (15) (solid curve), Eq. (16a) (dashed curve), and Eq. (16b) (dotted curve) with 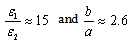 . Complex wave is showed by chain curve. Fig. 4 is an oversize.
. Complex wave is showed by chain curve. Fig. 4 is an oversize.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
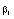 – real part and
– real part and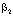 – imaginary part of the longitudinal propagation number,
– imaginary part of the longitudinal propagation number, 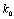 – the free-space wavenumber, b – the radius of a shield
– the free-space wavenumber, b – the radius of a shield