1. Introduction

Presently, millions of SPIMs in smaller sizes are in the commercial and domestic field. Therefore, even a minor improvement in the design of this kind of motors may save a vast electrical energy worldwide[1]. There are many types of SPIMs, depending upon the starting arrangement provided with the motor. Advances in the design of these motors have made an improvement in the power factor and efficiency of the motor. Split-phase, capacitor-start, shaded-pole and repulsion-type motors are quite popular from industrial viewpoint. Split phase single phase induction motor design is studied in this paper.

A number of works have reported the improvement of SPIMs efficiency so far. Active power loss effect in induction motor optimum design has proposed in[2]. The method of boundary search along active constraints and the Han-Powell method for optimization of single phase induction motor design have been presented in[3,4]. A triac-based drive with an optimal efficiency voltage controller is proposed in[5]. An appropriate method for motor efficiency maximization control, combined with a variable-speed drive, has been presented in[6]. Electrical machine design optimization using genetic algorithm has discussed in[7]. Some of the evolutionary algorithms for optimal design are available in the literatures[8-11].

This paper proposes a method for design optimization of single-phase induction motor to maximize the efficiency using particle swarm optimization (PSO). The present paper will be organized as follows. Section 2 briefly explains PSO algorithm. Section 3 presents relationships governing single-phase induction motor. Section 4 discusses the optimal design with variables and constraints. Section 5 gives the detailed discussion on the results of PSO algorithm and their comparison with conventional design.

2. Particle Swarm Optimization

PSO is a population-based, stochastic optimization algorithm based on the idea of a swarm moving over a given landscape. The algorithm adaptively updates the velocities and members positions of the swarm by learning from the good experiences. In PSO, the velocity v_i^d and position x_i^d of the dth dimension of the ith particle are updated as follows:

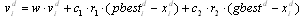(1)

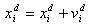(2)

Where

x_i :the position of the ith particle

v_i : the velocity of particle i

pbest_i :the best location in the search space ever visited by particle i

gbest :the best location discovered so far

w: the inertia weight that controls the impact of previous velocity of particle on its current one

r₁, r₂: independently uniformly distributed random variables with range (0, 1)

c1,c2 : positive constants(acceleration) coefficients which control the maximum step size.

In PSO, equation (1) is used to calculate the new velocity according to its previous velocity and to the distance of its current position from both its own best historical position and the best position of the entire population or its neighbourhood. Generally, the value of each component in v can be clamped to the range[-v_max, v_max] to control excessive roaming of particles outside the search space. Then the particle flies toward a new position according equation (2). This process is repeated until a user-defined stopping criterion is reached. A linearly decreasing inertia weight from maximum value w_max to minimum value w_min is used to update the inertia weight:

(3)

K_max is maximum iteration number[12,13].

3. Relationships Governing Single Phase Induction Motor

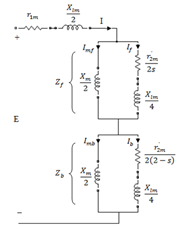Figure.1. equivalent circuit of SPIM based on double revolving field theory

Like other types of electrical machines, SPIMs are also designed to meet a given set of specifications. The motor has to be designed to give sufficient starting torque with reasonable performance during its working period. Fig. 1 illustrates equivalent circuit of SPIM based on double rotating field theory. The power flow diagram for a SPIM is shown in Fig. 2. Considering figures 1 and 2 relationships governing single phase induction motor may be expressed as follows[1]:

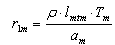(4)

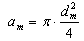(5)

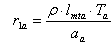(6)

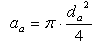(7)

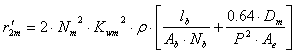(8)

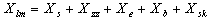(9)

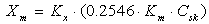(10)

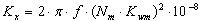(11)

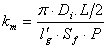(12)

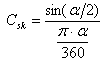(13)

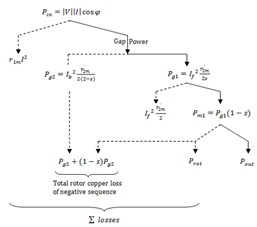Figure.2. power flow diagram for a SPIM

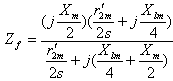(14)

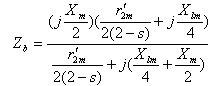(15)

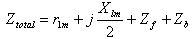(16)

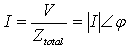(17)

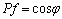(18)

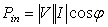(19)

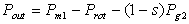(20)

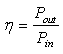(21)

Where:

r_1m, r_1a: Stator resistances of main and auxiliary winding, respectively

a_m, a_a: Area of the main and auxiliary winding conductor, respectively

d_m, d_a: Wire diameter of main and auxiliary winding, respectively

T_m,T_a: Number of turns in main and auxiliary winding, respectively

ŕ_2m: Rotor resistance

X_lm: Leakage reactance

X_m: Magnetizing reactance

X_s: Slot leakage reactance

X_zz: Zig zag leakage reactance

X_e: End leakage reactance

X_b: Belt leakage reactance

X_sk: Skew leakage reactance

D_i: Stator bore diameter

L: Stator stack length

P: Number of poles

V: Voltage

I: Current in main winding

f: Frequency

s: Rotor slip

Pf: Power Factor

K_wm: Winding factor

α: Skew of rotor

ρ: Copper resistivity

S₁: Number of stator slots

S₂: Number of rotor slots

l_mtm: Length of mean turn of the main winding

l_mta: Length of mean turn of the auxiliary winding

N_m: Number of conductors in stator main winding

l_b: Length of rotor bar

ĺ_g: Effective gap length

A_e: Area of the end ring

S_f: Saturation factor

D_m: Mean diameter of rotor

N_b: Number of rotor bars

A_b: Area of the rotor conductor

P_in: Input power

P_out: Output power

η: Efficiency

4. Optimal SPIM Design

The first optimization component is usually formulated is minimizing f(x) such that x exists within the n-dimensional feasible region D = {x│x≥0, g_i(x)≤0, i=1,2,…,m}. f(x), g_i(x) are real-valued scalar functions and vector x includes the n principal variables for which the optimization is to be performed. The function f(x) is called the “objective function”, for which the optimal values of x result in the minimum (maximum) of f(x), and these optimal values satisfy the given constraints. Inequality constraints g_i(x)≤ 0 include the performance properties of the motor, dimensional restrictions and additional requirements[3]. The following variables (x₁…x₆) are considered as the principal or independent variables of optimization:

x₁: Stator bore diameter (m)

x₂: Stator stack length (m)

x₃: Number of turns in main winding

x₄: Number of turns in auxiliary winding

x₅: Wire diameter of main winding (mm)

x₆: Wire diameter of auxiliary winding (mm)

The performance constraints imposed into induction motor design in this paper is as follows which are expressed in terms of variables:

1. Power factor at rated load

2. Locked rotor current to rated current ratio

3. Starting torque to full load torque ratio

4. Current density in the main winding

5. Current density in the auxiliary winding

The motor efficiency η has been taken as objective function to be maximized.

5. Results and Discussions

Table 1. Results of conventional and PSO based induction motor design Motor Parameters Conventional design PSO algorithm Stator bore diameter (m) 0.1 0.11227 Stator stack length (m) 0.06 0.045 Number of turns in main winding 184 206 Number of turns in auxiliary winding 262 270 Wire diameter of main winding (mm) 1.42 1.4381 Wire diameter of auxiliary winding (mm) 0.711 0.7377 Efficiency (%) 0.7859 0.8053 Power factor 0.8324 0.8324 Starting torque to full load torque ratio 0.7570 0.7576 Full load slip 0.0366 0.0332

Table 2. Parameters of the PSO Parameters Value Population size 100 dimension number 6 Max iteration 200 wmax 0.9 wmin 0.4 c1 2 c2 2

The PSO algorithm is implemented to optimize the design of induction motor whose specifications are available in appendix. Results are compared with conventional design and tabulated in table 1. It is observed from the table that the efficiency of the induction motor has increased using PSO compared to the conventional design. Full load slip in PSO is smaller than conventional design. Starting torque to full load torque ratio is slightly better than the other. The PSO algorithm parameters used in this paper are tabulated in table 2 which determined by trial and error method by using computer simulations. Fig. 3 shows the variations of efficiency against the PSO iteration number during the optimization process. The variations of motor efficiency verse the output power and rotor slip are shown in figures 4 and 5, respectively. From figures 4 and 5, it is obvious that maximum efficiency is achieved at the rated output power with rotor slip of 0.0332.

6. Conclusions

The application of particle swarm optimization (PSO) in parameters design of a split-phase single-phase induction motor is investigated in this paper. The induction motor design optimization is formulated as a nonlinear programming problem and the motor efficiency is considered as objective function. . It was observed that the efficiency of the induction motor was increased using PSO compared to the conventional design and full load slip in PSO was smaller than conventional design. The main advantages of the proposed technique are; its simple structure and its straightforward verification of maximum efficiency of induction motor for a given output power. The PSO offered better results compared with conventional design and it is more suitable to design optimization of single phase induction motor.

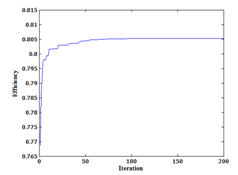Figure 3. Variation of efficiency against PSO iteration number

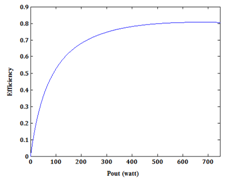Figure 4. Variation of designed motor efficiency against output power

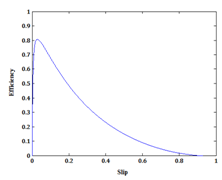Figure 5. Variation of motor efficiency against rotor slip

Appendix

Specifications of SPIM motor:

Capacity 1 hp

Voltage 115 V

Frequency 50 Hz

Number of poles 2

Number of stator slots 24

Number of rotor slots 30