1. Introduction

Electrical tree growth mechanisms have been modelled resorting to various approaches, from physical to purely phenomenological, which were investigated extensively during the last few decades and are still under study[1-4].

Considerable steps forward in the increase of knowledge on this phenomenon came from the possibility to carry out simultaneous PD and electroluminescence measurements[3].

A precursor model was presented in[1], which holds for initiation and growth of electrical trees in polymeric cable insulation. It assumes that local stress enhancements, which can take place in insulation due, for example, to contaminants or protrusions, cause inception of PD in adjacent small cavities once the electric field exceeds a threshold value. Electric charges thus penetrate into the insulation, giving rise to channels which form the electrical tree and grow with time until breakdown Experimental Setup[1].

The electric field plays an important role for electrical tree initiation, but this field produced from non-uniform edge which causes difficulty of this field calculation.

A simulation program with artificial intelligent, (geneticalgorithms), software is required to calculate and simulate this field for fast and accurate detection of tree location and initiation.

2. Electrical Field Calculation

In the study of electrical breakdown of dielectric, and the design of high voltage devices a complete knowledge of electric field distribution is very important[5-10].

There are different methods available for the prediction of electric field in a given geometrical arrangement of conductors. These methods are classified into graphical, analogue, analytical and numerical.

The progress of electrical trees in an insulating system calls at first for accurate computation of the electrostatic field. This is obtained from Laplace's equation using charge simulation method CSM[1,6-8]. The needle electrode is simulated by a number of ring charges. The appropriate arrangement of these ring charges is achieved by genetic algorithms GAs[6,8].

At the needle tip the electric field must reach a value of 4 MV/cm[1] for tree inception. A software program is introduced to calculate the electric field and indicate if it is lower than, equal or higher than the critical value 4 MV/cm, so the tree prediction can be classify according to this value.

2.1. Needle Simulation

Figure 1 shows a hyperbolic needle-to-plane electrode system which is stressed by a voltage 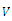and embedded in solid insulation.

The needle has a tip radius 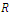and is located at spacing 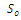above the grounded plane.

The shape of the needle may be described by the hyperbolic function[11]:

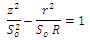The distributed charge on the needle surface is simulated by a set of n ring charges arranged along the needle axis. The vector of unknown charges, 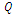is computed from the matrix equation: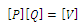

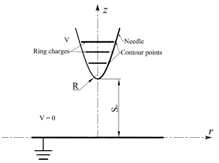Figure 1. A hyperbolic needle-to-plane gap configuration

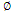For a given charge distribution, the potential at an arbitrary point is a summation of the potentials resulting from the individual charges,

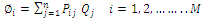where 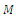and 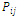are the number of contour points, (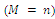) and potential coefficients, respectively.

The field stress is calculated by superposition of magnitudes of various directional components. For example, in the Cartesian coordinate system, the net field 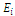at point 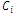is given by

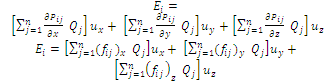where, 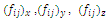, are the ‘field intensity’ or field coefficients and 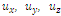are unit vectors in the 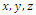directions, respectively. In many cases, the electrostatic field between a system of conductors and an infinite plane with 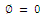is of interest.

Electric field calculation in the dielectric medium in this software satisfies the Laplace’s equation,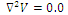

3. Software Design

Graphical user interface GUI under Matlab2010 has been used in the software design for electric field calculation. The required input data are the applied voltage of the cable, the insulation thickness, the needle tip radius, and the relative permittivity of the dielectric material. Figure 2 shows the screen for the software using in the electric field calculation.

This software is: easy to use, cheap, does not require experienced operator, gives a new classification of the underground cables depending on the electric field value produced from the sharp edge, which increase the price of high class cables.

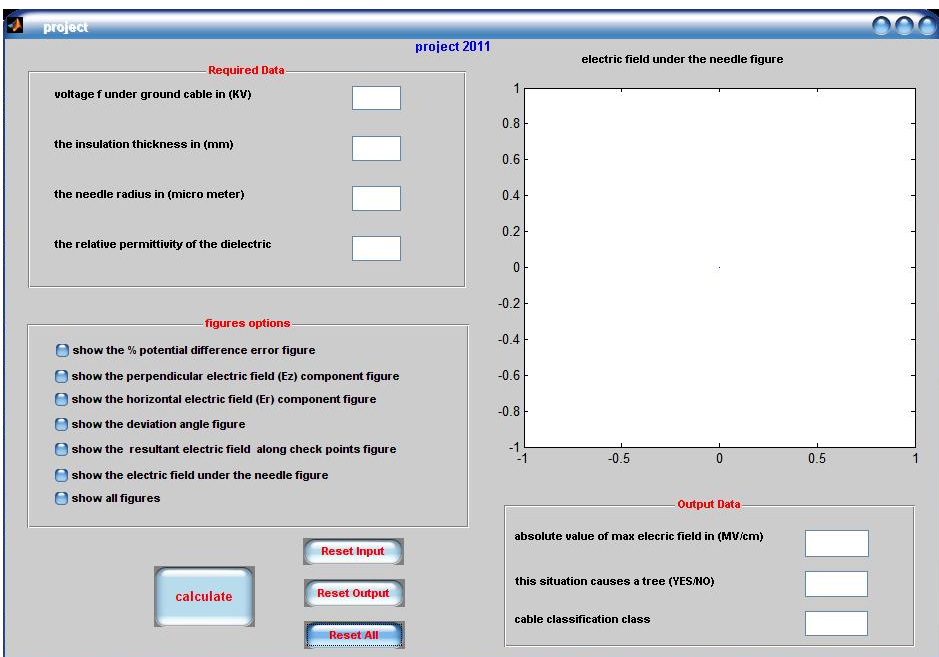Figure 2. Software screen for electric field calculation

Table 1. The output from software program for case one 10 kV 9.5 kV 9 kV 8.5 kV 8 kV Radius in (µm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Y 5.76894 Y 5.48049 Y 5.19205 Y 4.9039 Y 4.6152 3 Y 4.45528 Y 4.23251 Y 4.00975 N 3.78699 N 3.5642 4 N 3.65214 N 3.46954 N 3.28693 N 3.10432 N 2.921 5 N 3.10783 N 2.95244 N 2.79705 N 2.64166 N 2.4863 6 N 2.7133 N 2.57763 N 2.44197 N 2.3063 N 2.1706 7 N 2.41347 N 2.29279 N 2.17212 N 2.05145 N 1.9308 8 N 2.17745 N 2.06857 N 1.9597 N 1.85083 N 1.742 9 N 1.98654 N 1.88721 N 1.78789 N 1.68856 N 1.589 10 N 1.82875 N 1.73731 N 1.64587 N 1.55443 N 1.463 11 N 1.696 N 1.6112 N 1.5264 N 1.4416 N 1.3568 12 N 1.58268 N 1.50355 N 1.42441 N 1.34528 N 1.3568 13 N 1.48474 N 1.4105 N 1.33626 N 1.26203 N 1.2661 14

Table 2. The output from software program for case two 10 kV 9.5 kV 9 kV 8.5 kV 8 kV Radius in (µm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Tree(Y/N) Max field in(MV/cm) Y 5.86339 Y 5.57022 Y 5.27705 Y 4.98388 Y 4.69071 3 Y 4.53443 Y 4.30771 Y 4.08099 N 3.85426 N 3.62754 4 N 3.72077 N 3.53473 N 3.34869 N 3.16265 N 2.97661 5 N 3.16873 N 3.01029 N 2.85186 N 2.69342 N 2.53498 6 N 2.76827 N 2.62986 N 2.49144 N 2.35303 N 2.21462 7 N 2.46373 N 2.34054 N 2.21736 N 2.09417 N 1.97098 8 N 2.22388 N 2.11268 N 2.00149 N 1.89029 N 1.7791 9 N 2.02978 N 1.92829 N 1.8268 N 1.72531 N 1.62382 10 N 1.86928 N 1.77582 N 1.68235 N 1.58889 N 1.49542 11 N 1.73421 N 1.6475 N 1.56079 N 1.47408 N 1.38737 12 N 1.61887 N 1.53793 N 1.45699 N 1.37604 N 1.2951 13 N 1.51916 N 1.4432 N 1.36724 N 1.29128 N 1.21533 14

4. Results

Case one: for PVC dielectric used in underground cable, Cable voltage (8-10) kV, Cable insulation thickness = 5.2 mm, Cable insulation material (PVC) permittivity = 8.

Table 1 represents the output from the software program for case one.

Case two: for XLPE dielectric used in underground cable, Cable voltage (8-10) kV, Cable insulation thickness = 3.4 mm, Cable insulation material permittivity = 2.3.

Table 2 represents the output from the software program for case two.

5. Conclusions

The new software program presents a very simple method for calculation of a non-uniform electric field for hyperbolic needle-to-plane problem by using CSM combined with GAs and indicates the case for electrical tree formation in underground cable.

This software is easy and does not require experienced operator, also it gives a new classification of the cables and reduced the effort required to indicate the fault location of the cables. This classification depending on the electric field value produced from the sharp edge which can be indicating in the manufacturing process before using the cables.

The software can classify the high standard cables which increase its price.

ACKNOWLEDGEMENTS

The author thanks Prof. A. El-Zein and Prof. M. M. El Bahy for their support and understanding of electrical tree mechanisms and simulation methods.