1. Introduction

The transmission of data at high rate is the basic need in modern communication system. For this purpose, the frequency independent antenna with coverage of wide range of frequencies is the ultimate goal. One of the most powerful and popular method for such type of applications is the designing of Log Periodic Dipole Antenna (LPDA) which was the endeavour of Isbell and Carrel[1,2].

A Log Periodic Dipole Antenna is a wideband antenna that is not affected by changing the spectrum of frequencies within the desired band[3]. LPDA consist of number of elements having unequal lengths, spacing and diameters. The prelursory work of[1,2] presented the precise designing of LPDA. The basic response of LPDA has been analysed by the mathematical formulas introduced by[1,2]. The behaviour of current across each dipole element is the main task for the response of LPDA. The prerequisite condition described by[4] which was used to find current and impedance between parallel antennas of unequal lengths.

In the mid 1990’s, the evolutionary technique was introduced by Kennedy and Eberhart[5] namely Particle Swarm Optimization (PSO). The use of this algorithm is a very smart approach to many electromagnetic problems. This algorithm has been used due to fast convergence, simple implementation, less computation and generally few lines of code[6-7]. There are numerous optimization techniques are frequently applied in many electromagnetic related problems[8-15]. Out of those techniques, PSO and its differentvaria- nts are considered powerful optimization tools which offer almost guaranteed convergence for complex problems[5-6].

With the aid of[1,2], we calculate the basic response of LPDA and then this design is optimized using PSO. This technique minimizes the design of LPDA as compared to the initial design. Moreover, it is observed that how this computational algorithm alters the gain and VSWR of Log Periodic Dipole Antenna as compared to the standard of LPDA.

2. Design and Simulation of LPDA

Log Periodic Dipole Antenna (LPDA) has some endless benefits which are high gain and optimum VSWR. Due to these benefits, it is extensively used in many applications. LPDA was first introduced in University of Illinios by Carrel in 1960[2].

The schematic diagram of LPDA is shown in Fig. 1 which consists of number of dipole elements having unequal lengths, spacing and diameters. The step by step design procedure of LPDA is described by[16-17]. The basic design equations are used to determine different parameters of LPDA which are given below

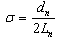(1)

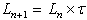(2)

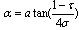(3)

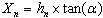(4)

The spacing between every two consecutive elements is determined by using eq. (2). σ is a spacing factor in the range of 0.04 ≤ σ ≤ 0.22[18]. Eq. (3) is used to determine the length of each element in which τ is a scaling factor in the range of 0.76 ≤ τ ≤ 1. The distance from source to any dipole element is determined by eq. (4). The initial response of LPDA is observed against the design using τ = 0.9, σ = 0.16, N = 13, L_n/d_n = 125, Z_o = 100 Ω and L₁ = λ_ref × 0.5, respectively. Where, λ_ref is calculated from reference frequency which is 400 MHz in our case. This reference frequency is used to define the length of first dipole element. The rest of the lengths of each dipole element and other parameters are calculated from the design equations which discussed above. The design parameters corresponding to each dipole element are given in Table 1.

Where, h_n is the length of n^th element and X_n is the distance from source to n^th dipole element, respectively. The response is being calculated as discussed in[17]. The important factor is to determine the current across each dipole element which can be determined by knowing the impedance of each dipole element and admittance of feeder line as step by step procedure which discussed in[17]. The method of moment is being used to determine the impedance across each dipole element[4]. The admittance of feeder line is determined by a method as discussed in[2]. The initial response is taken by implementing a MATLAB routine against the design parameters. The initial response is compared with[18] which include gain and VSWR. The initial gain for different communication bands are shown in Fig. 2-5. The overall initial VSWR for the reported bands is shown in Fig. 6.

Table 1. Initial LPDA Design Element # Ln (m) hn (m) Xn (m) Dn (m) dn (m) 1 0.375 0.1875 0.0437 0.12 0.003 2 0.3375 0.1688 0.0394 0.108 0.0027 3 0.3038 0.1519 0.0354 0.0972 0.0024 4 0.2734 0.1367 0.0319 0.0875 0.0022 5 0.246 0.123 0.0287 0.0787 0.002 6 0.2214 0.1107 0.0258 0.0709 0.0018 7 0.1993 0.0996 0.0232 0.0638 0.0016 8 0.1794 0.0897 0.0209 0.0574 0.0014 9 0.1614 0.0807 0.0188 0.0517 0.0013 10 0.1453 0.0726 0.0169 0.0465 0.0012 11 0.1308 0.0654 0.0153 0.0418 0.001 12 0.1177 0.0588 0.0137 0.0377 0.0009 13 0.1059 0.053 0.0124 ― 0.0008

3. Particle Swarm Optimization

Kennedy and Eberhart[5] was the pioneer of Particle Swarm Optimization (PSO), who proposed this evolutionary algorithm which based on group intelligence. It is our common observation in our daily life that different species like birds, bees, etc. travel from one place to another for the search of food. Every individual particle, in our case is bird, has its own local best or pbest which is determined by its location in the swarm. On the other hand, each bird has some way of knowing the more concentration of food discover by the whole swarm. This location is known as global best or gbest. The gbest is the only location in the whole swarm where every bird desires to achieve its best position. For the optimum solution, there must be a fitness function which search in the entire solution space of swarm and produce single number of position[19].

For an optimum solution, random positions and velocities of the swarm particles are initialized to optimize the parameters. However, the restriction on the positions and the velocities of the particles is applied to keep the particles in search area to avoid the unrealistic solution. The optimized parameters of any problem define the dimensions of the problem. The updated positions and velocities are determined by the following equations.

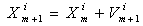(5)

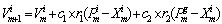(6)

Where, Xⁱ_m is the particle position, Vⁱ_m is the particle velocity, Pⁱ_m is the best individual particle position, P^g_m is the best swarm particle position and m represents number of iterations in the whole swarm. c₁ and c₂ determines relative push of pbest and gbest in the entire swarm. r₁ and r₂ exists in the range of (0,1). The velocities are scaled by inertia weight w which consequently changes the direction of pbest and gbest for specific dimension.

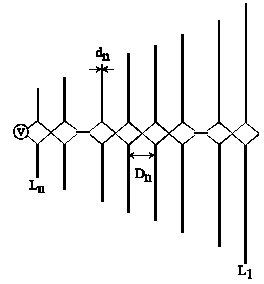Figure 1. Geometry of Log Periodic Dipole Array

4. Implementation of PSO

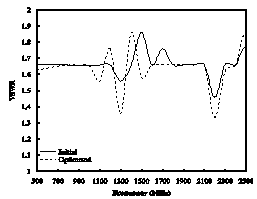
PSO is implemented on 13 dipole elements of LPDA with the goal to reduce the computational cost of optimization algorithm to a considerable time. So, number of dimensions of the optimization is set as low as possible. The number of parameters to be optimized for a given problem defines dimensions of the entire swarm. The dimensions of the swarm are chosen to form only 13 design elements. In swarm, every particle is responsible to define the length of first element and rest of the lengths, spacing and diameters. Hence, the physical dimensions of optimized antenna are depending on the swarm particles which define the length of the first dipole element. The fitness function consists on a condition to improve gain as compared to the initial one with optimum VSWR. The minimum and maximum velocities are 0 and 0.2, respectively, and the particles are in the range of[0.6-1.1]. The position and the velocity of the particle are updated by using eqs. (5) and (6). After simulation, we get an optimum design of LPDA which is shown in Table 2.

The optimum solution of gain and VSWR against these parameters is shown in Fig. 2-6. The comparison between the initial and optimized gain for reported frequency bands is shown in Fig. 2-5. It is clear from the figures that the presented optimization technique gives better response for gain than the initial one. From Fig. 6, it is observed that the initial mean VSWR reduce to its ideal value which is ≤ 1.5.

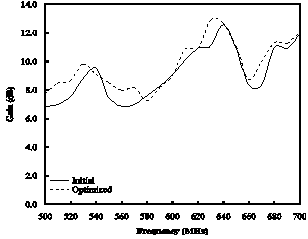Figure 2. Initial and optimized gain for WiMAX frequency band

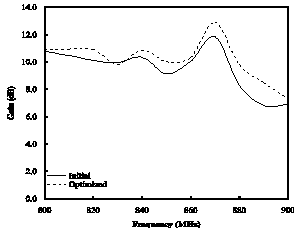Figure 3. Initial and optimized gain for GSM-I

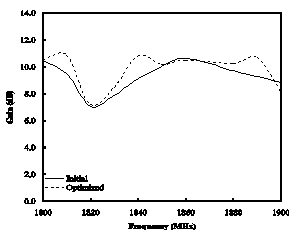Figure 4. Initial and optimized gain for GSM-

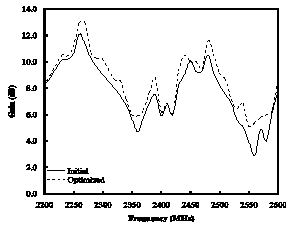Figure 5. Initial and optimized gain for Bluetooth®, Wi-Fi and 3G mobile communication bands

Figure 6. Initial and optimized VSWR

Table 2. Optimized LPDA Design Using PSO Element # Ln (m) hn (m) Xn (m) Dn (m) dn (m) 1 0.2213 0.1106 0.0258 0.0708 0.0018 2 0.1991 0.0996 0.0232 0.0637 0.0016 3 0.1792 0.0896 0.0209 0.0573 0.0014 4 0.1613 0.0806 0.0188 0.0516 0.0013 5 0.1452 0.0726 0.0169 0.0465 0.0012 6 0.1306 0.0653 0.0152 0.0418 0.001 7 0.1176 0.0588 0.0137 0.0376 0.0009 8 0.1058 0.0529 0.0123 0.0339 0.0008 9 0.0952 0.0476 0.0111 0.0305 0.0008 10 0.0857 0.0429 0.01 0.0274 0.0007 11 0.0771 0.0386 0.009 0.0247 0.0006 12 0.0694 0.0347 0.0381 0.0222 0.0006 13 0.0625 0.0312 0.0073 ― 0.0005

5. Conclusions

The LPDA is designed and then it is optimized by using stochastic technique called Particle Swarm Optimization (PSO). All work is done by writing a MATLAB routine and the results are shown. It is observed that the optimum solution for gain for WiMAX, GSM phase (I and II), Bluetooth^® and 3G mobile communication bands has been improved up to 0.6 dB, 0.7 dB, 0.6 dB and 0.8 dB, respectively. It is also observed that the unequal length, spacing and diameter of each dipole element is reduced as compared to the standard design. The VSWR is also reduced to its acceptable value which is ≤ 1.5.