M. Zakaria 1, 2
1Mathematics department, Faculty of Education, El-Shatby Alexandria University, Alexandria, 21526, Egypt
2Department of Mathematics, Faculty of Science, Al-Baha University, Al-Baha, P.O. Box 1988, Kingdom of Saudi Arabia
Correspondence to: M. Zakaria , Mathematics department, Faculty of Education, El-Shatby Alexandria University, Alexandria, 21526, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this work, a two dimensional problem in magnetic micropolar generalized thermoelastic medium, in the presence of a transverse magnetic field -taking into consideration the effect of Hall current- subjected to ramp-type heating, is investigated. The entire elastic medium is rotating with a uniform angular velocity. Laplace-Fourier transform technique is used to solve the problem. The transformed components of normal strain, normal stress, tangential couple stress, temperature distribution, and the current density components are obtained. The integral transforms have been inverted by using a numerical technique. Hall current effects and effect of rotation have been depicted graphically on the resulting quantities.
Keywords:
Keywords Hall Current, Micropolar, Thermoelasticity, Ramp-Type Heating
1. Introduction
The linear theory of elasticity is of paramount importance in the stress analysis of steel, which is the commonest engineering structural material. To a lesser extent, linear elasticity describes the mechanical behavior of the other common solid materials, e.g. concrete, wood and coal. However, the theory does not apply to the behavior of many of the new synthetic materials of the elastomer and polymer type, e.g. polymethyl-methacrylate (Perspex), polyethylene and polyvinyl chloride. The linear theory of micropolar elasticity is adequate to represent the behavior of such materials. For ultrasonic waves i.e. for the case of elastic vibrations characterized by high frequencies and small wavelengths, the influence of the body microstructure becomes significant. This influence of microstructure results in the development of new type of waves, not found in the classical theory of elasticity. Metals, polymers, composites, soils, rocks, concrete are typical media with microstructures. More generally, most of the natural and manmade materials including engineering, geological and biological media possess a microstructure. Eringen and Suhubi[1] and Suhubi and Eringen[2] developed the nonlinear theory of micro-elastic solids. Later Eringen[3-5] developed a theory for the special class of micro-elastic materials and called it the“linear theory of micropolar elasticity”. Under this theory, solids can undergo macro-deformations and macro-rotations. The classical uncoupled theory of thermoelasticity predicts two phenomena not compatible with physical observations. First, the equation of heat conduction of this theory does not contain any elastic terms, second, the heat equation is of a parabolic type, predicting infinite speeds of propagation for heat waves.Biot[6] introduced the theory of coupled thermoelasticity to overcome the first shortcoming. The governing equations for this theory are coupled, eliminating the first paradox of the classical theory. However, both theories share the second shortcoming since the heat equation for the coupled theory is also parabolic.Two generalizations to the coupled theory were introduced. The first is due to Lord and Shulman[7], who obtained a wave-type heat equation by postulating a new law of heat conduction to replace the classical Fourier’s law. Since the heat equation of this theory is of the wave-type, it automatically ensures finite speeds of propagation for heat and elastic waves. The remaining governing equations for this theory, namely, the equations of motion and constitutive relations, remain the same as those for the coupled and the uncoupled theories. The second generalization is known as the theory of thermoelasticity with two relaxation times, or the theory of temperature-rate-dependent thermoelasticity, and was proposed by Green and Lindsay[8]. It is based on a form of the entropy inequality proposed by Green and Laws[9]. It does not violate Fourier’s law of heat conduction when the body under consideration has a center of symmetry, and it is valid for both isotropic and anisotropic bodies. Ezzat and Youssef[10] studied the generalized magneto-thermoelasticity in a perfectly conducting medium. The foundations of magnetoelasticity were presented by Knopoff[11] and Chadwick[12] and developed by Kaliski and Petykiewicz[13]. An increasing attention is being devoted to the interaction between magnetic field and strain field in a thermoelastic solid due to its many applications in the fields of geophysics, plasma physics and related topics. In all papers quoted above it was assumed that the interactions between the two fields take place by means of the Lorentz forces appearing in the equations of motion and by means of a term entering Ohm’s law and describing the electric field produced by the velocity of a material particle, moving in a magnetic field.Many authors have considered the propagation of electromagneto-thermoelastic waves in an electrically and thermally conducting solid. Paria[14] discussed the propagation of plane magneto-thermoelastic waves in an isotropic unbounded medium under the influence of a uniform thermal field and with a magnetic field acting transversely to the direction of the propagation. Paria used the classical Fourier law of heat conduction, and neglected the electric displacement. Wilson[15] extended Paria’s results by introducing a component of the magnetic field parallel to the direction of the propagation. A comprehensive review of the earlier contributions to the subject can be found in Paria[16]. Among the authors who considered the generalized magneto-thermoelastic equations are Nayfeh and Namat-Nasser[17] who studied the propagation of plane waves in a solid under the influence of an electromagnetic field. They obtained the governing equations in the general case and the solution for some particular cases. Choudhuri[18] extended these results to rotating media. Sherief and Ezzat[19] solved a thermal shock half-space problem using asymptotic expansions. Lately, Rajneesh Kumar and Rupender[20] studied the effect of rotation in magneto-micropolar thermoelastic medium due to mechanical and thermal sources, Rajneesh Kumara and ManjeetSingh[21] solved the effect of rotation and imperfection on reflection and transmission of plane waves in anisotropic generalized thermoelastic media, R. Kumar, Praveen Ailawalia[22] studied moving load response in micropolar thermoelastic medium without energy dissipation possessing cubic symmetry, few attempts have been made to solve two-dimensional problems in this field Moncef Aouadi[23] introduced temperature dependence of an elastic modulus in generalized linear micropolar thermoelasticity.When the magnetic field is very strong, the conductivity will be a tensor and the effect of Hall current cannot be neglected. The conductivity normal to the magnetic field is reduced due to the free spiraling of electrons and ions about the magnetic lines of force before suffering collisions and a current is induced in a direction normal to both the electric and magnetic fields. This phenomenon is called the Hall effect. In all of the above investigations, the effects of Hall current have not been considered. In this work, we introduced a new model of the equations of the generalized magneto micropolar thermoelasticity in the presence of transverse magnetic field, taking into consideration the effects of Hall current and rotation, is applied to both generalizations, Lord–Shulman theory and Green–Lindsay theory, as well as to the coupled theory.
2. Basic Equations
In the dynamical of linear theory of magneto micropolar thermoelasticity permeated by an initial strong magnetic field of strength H = (0, 0, Ho). We consider The elastic medium is rotating uniformly with an angular velocity Ω. The governing equations of motion for homogenous, isotropic and elastic solid, when the Hall current and rotation effect is taken into account consists ofi. The equations of motion taking into account the Lorentz force have the form | (1) |
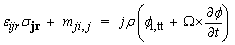 | (2) |
where σij is the force stress tensor, ui is the components of the displacement vector, φi is the components of the microrotation vector, mij is the couple stress tensor, ρ is the density, j is the microinertia, εijr is the permutation symbol, µo is the magnetic permeability, and Jr is the conduction current density, given by The generalized Ohm’s law including Hall current: 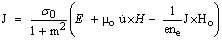 | (3) |
where E is the intensity vector of the electric field, m (= ωe te) is the Hall parameter, te is the electron collision time, ωe (= e Bo/me) is the electronic frequency, e is the charge of an electron, Bo is the magnetic induction, me is the mass of the electron, σo (e2 ne te/me), is the electrical conductivity and ne is the number density of electrons.ii. The constitutive equation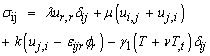 | (4) |
 | (5) |
where λ, μ are Lame’s constants, α, β, γ, and k are micropolar constants, T is the absolute temperature of the medium, ν is the constant with dimension of time, called relaxation time, γ1 is the material constant given by γ1 = ( 3 λ+2μ+K) α1, α1 being a coefficient of linear thermal expansion. iii. The generalized equation of heat condition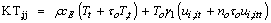 | (6) |
where K is thermal conductivity, cE is the specific heat at constant temperature, To is the uniform temperature, τo is an other relaxation time and no is a non-dimensional constant. For L–S theory n0 =1, τo > 0, ν = 0, and for G–L theory n0 = 0, τo > 0, ν > 0. Substituting equations (4), and (5) into equation (5), and (6) we get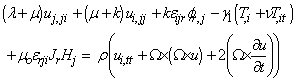 | (7) |
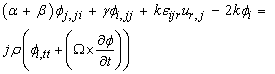 | (8) |
3. Formulation and Solution of the Problem
The rectangular Cartesian system (x, y, z) having origin on the surface z = 0 with z-axis vertical into the medium is introduction. In the following, we restrict our analysis parallel to xz-plane with z  0, ui = (u, 0, w), φi = (0, φ2, 0) and Ω = (0, Ω, 0), we also assume that E = 0, the generalized Ohm’s law gives Jy = 0 everywhere in the medium. The current density components Jx and Jz are given by:
0, ui = (u, 0, w), φi = (0, φ2, 0) and Ω = (0, Ω, 0), we also assume that E = 0, the generalized Ohm’s law gives Jy = 0 everywhere in the medium. The current density components Jx and Jz are given by: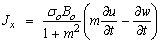 | (9) |
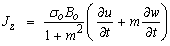 | (10) |
Let us introduce the following non-dimensional variables: where
where 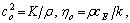 and M is the Hartmann number or magnetic parameter.The system of equations (6)-(8), using relations (9), and (10), takes the following form – dropping the asterisks for convenience-,
and M is the Hartmann number or magnetic parameter.The system of equations (6)-(8), using relations (9), and (10), takes the following form – dropping the asterisks for convenience-,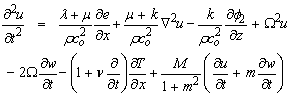 | (11) |
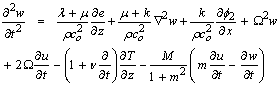 | (12) |
 | (13) |
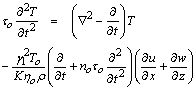 | (14) |
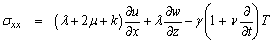 | (15) |
 | (16) |
 | (17) |
 | (18) |
 | (19) |
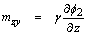 | (20) |
Introducing potential functions Φ(x,z,t), and Ψ(x,z,t) defined by | (21) |
Substituting Eq. (21) into Eqs. (11)–(14) we obtain | (22) |
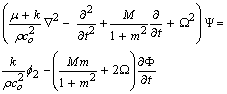 | (23) |
 | (24) |
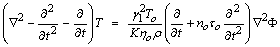 | (25) |
Taking Laplace transform defined by the relation: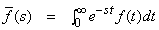 of both sides of (15)–(20) and (22)-(25) using the homogenous initial conditions, we obtain:
of both sides of (15)–(20) and (22)-(25) using the homogenous initial conditions, we obtain: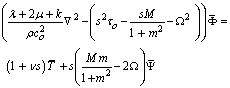 | (26) |
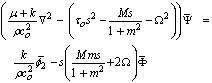 | (27) |
 | (28) |
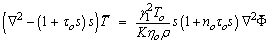 | (29) |
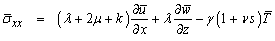 | (30) |
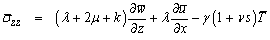 | (31) |
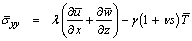 | (32) |
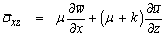 | (33) |
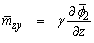 | (33a) |
We now use the Fourier transform with respect to the space variable z, defined by Taking the Fourier transform of both sides of (26)–(33)
Taking the Fourier transform of both sides of (26)–(33) | (34) |
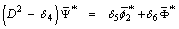 | (35) |
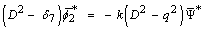 | (36) |
 | (37) |
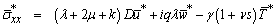 | (38) |
 | (39) |
 | (41) |
 | (42) |
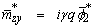 | (43) |
where 
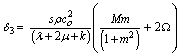
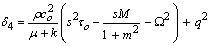
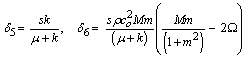
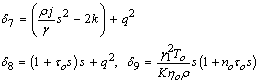 and the operator D means the derivative with respect to x.0n Eqs. (34)–(37) and after some simplification, we arrive at the followingeighth order differential equation satisfied by
and the operator D means the derivative with respect to x.0n Eqs. (34)–(37) and after some simplification, we arrive at the followingeighth order differential equation satisfied by 
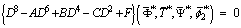 | (44) |
where 


 The solution of the Eq. (44) satisfying the radiation conditions that
The solution of the Eq. (44) satisfying the radiation conditions that 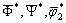 and
and 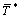 tend to zero as x tends to infinity can be written as
tend to zero as x tends to infinity can be written as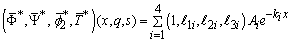 | (45) |
where 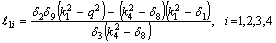
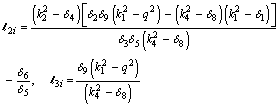 and ki (i=1,2,3,4) are the characteristic roots of the characteristic equation (36) which is
and ki (i=1,2,3,4) are the characteristic roots of the characteristic equation (36) which is Eq. (21) together with Eq. (45), immediately give
Eq. (21) together with Eq. (45), immediately give | (46) |
 | (47) |
4. Application
The boundary of the half-space is affected by ramp-type heating, which depends on the coordinate z and the time t of the form | (48) |
where F(z) is an arbitrary function of z and G(t) is a function defined as Misra et al.,[25]: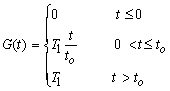 | (49) |
where to indicates the length of time to rise the heat and T1 is constant, this means that the boundary of the half-space, which is initially at rest and has a fixed temperature To, is suddenly raised to a temperature equal to the function G(t)F(z) and maintained at this temperature from then on.Applying the Laplace and Fourier transforms to both sides of Eq. (42), we obtain | (50) |
where  We assume that, on the boundary x = 0 the displacement u of the body does not depends on x, hence we have Du(0, z, t) = 0 and the medium is subjected to a rough and rigid foundation enough to prevent the displacement w at any time and any point of z, so also we have w(0, x, t) = 0, mzy = 0.Applying the Laplace and Fourier transforms, we get
We assume that, on the boundary x = 0 the displacement u of the body does not depends on x, hence we have Du(0, z, t) = 0 and the medium is subjected to a rough and rigid foundation enough to prevent the displacement w at any time and any point of z, so also we have w(0, x, t) = 0, mzy = 0.Applying the Laplace and Fourier transforms, we get | (51) |
Using the values in expressions (50), and (51), the above general expressions reduce in our case to the following form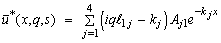 | (52) |
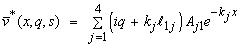 | (53) |
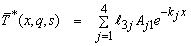 | (54) |
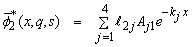 | (55) |
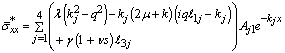 | (56) |
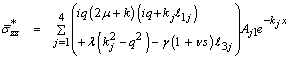 | (57) |
 | (58) |
 | (59) |
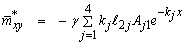 | (60) |
 | (61) |
where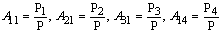



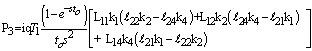


5. Particular Cases
i- If m = 0, in Eqs. (52)–(61), we obtain the components of displacements and tresses in magneto-micropolar generalized thermoelastic with rotating medium without Hall current effect.ii- Taking Hartmann number M = 0, in Eqs. (52)–(61), we obtain the components of displacements and tresses in micropolar generalized thermoelastic with rotating medium.iii. If the effect of rotation is absent (Ω = 0), in Eqs. (52)–(61), we obtain the components of displacements and stresses in micropolar generalized thermoelastic medium with the following changed values of δ1, δ3, δ4, and δ6 as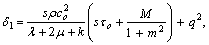
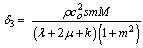
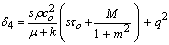
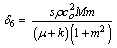 iv. Taking n0 =1, τo > 0, ν = 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for L–S theory.v. Taking n0 = 0, τo > 0, ν > 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for G–L theory.vi. Taking, n0 = 0, τo= 0, ν= 0 we obtain the corresponding expressions for magneto-micropolar coupled thermoelastic with rotating medium for (C–T theory
iv. Taking n0 =1, τo > 0, ν = 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for L–S theory.v. Taking n0 = 0, τo > 0, ν > 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for G–L theory.vi. Taking, n0 = 0, τo= 0, ν= 0 we obtain the corresponding expressions for magneto-micropolar coupled thermoelastic with rotating medium for (C–T theory
6. Inversion of the Transforms
To obtain the solution of the problem in the physical domain (x,y, t), we have to invert the iterated transforms in Eqs. (52)–(61). These expressions can be formally expressed as functions of x and the parameter of the Fourier and Laplace transforms q and s of the form  .First, we invert the Fourier transform using the inversion formula given previously. This gives the Laplace transform expression
.First, we invert the Fourier transform using the inversion formula given previously. This gives the Laplace transform expression 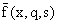 of the function f(x,y, t) as
of the function f(x,y, t) as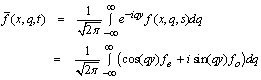 where fe and fo denote the even and the odd parts of the function
where fe and fo denote the even and the odd parts of the function 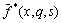 respectively.We shall now outline the numerical inversion method used to find the solution in the physical domain. For fixed values of x, y, and q the function inside braces in the last integral can be considered as a Laplace transform
respectively.We shall now outline the numerical inversion method used to find the solution in the physical domain. For fixed values of x, y, and q the function inside braces in the last integral can be considered as a Laplace transform  of some function g(t).The inversion formula for the Laplace transform can be written as
of some function g(t).The inversion formula for the Laplace transform can be written as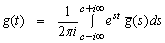 where c is an arbitrary real number greater than all the parts of the singularities
where c is an arbitrary real number greater than all the parts of the singularities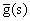 . Taking s = c + iy, the above integral takes the form
. Taking s = c + iy, the above integral takes the form Expanding the function h(t) = exp(-ct)g(t) in a Fourier series in the interval[0, 2L], we obtain the approximate formula.
Expanding the function h(t) = exp(-ct)g(t) in a Fourier series in the interval[0, 2L], we obtain the approximate formula.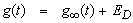 where
where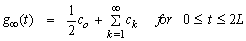 | (62) |
and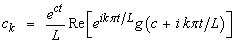 | (63) |
ED, the discretization error, can be made arbitrary small by choosing c large enough.Since the infinite series in Eq. (62) can be summed up to finite number N of terms, the approximate value of g(t) becomes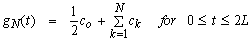 | (64) |
Using the above formula to evaluate g(t), we introduce a truncation error ET which, must be added to the discretization error to produce the total approximation error.Two methods are used to reduce the total error. First the ‘‘Korrecktur’’ method is used to reduce the discretization error. Next, the e algorithm is used to reduce the truncation error and hence to accelerate convergence.The Korrecktur method uses the following formula to evaluate the function g(t):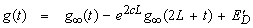 where the discretization error
where the discretization error 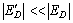 . Thus, the approximate value of g(t) becomes
. Thus, the approximate value of g(t) becomes | (65) |
N' is an integer such that N' < N.We shall now describe the e-algorithm that is used to accelerate the convergence of the series in Eq. (64).Let N = 2q + 1 where q is a natural number, and let be the sequence of partial sums of Eq. (64). We define the e-sequence by
be the sequence of partial sums of Eq. (64). We define the e-sequence by and
and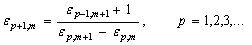 it can be shown that the sequence ε1,1, ε3,1, ε5,1, . . . , εN,1, converges to f(x,y, t) + ED – co/2 faster than the sequence of partial sums sm (m = 1,2,3,. . .).The actual procedure used to invert the Laplace transform consists of using Eq. (65) together with the ε-algorithm. The values of c and L are chosen according to the criteria outlined Honig and Hirdes[24].
it can be shown that the sequence ε1,1, ε3,1, ε5,1, . . . , εN,1, converges to f(x,y, t) + ED – co/2 faster than the sequence of partial sums sm (m = 1,2,3,. . .).The actual procedure used to invert the Laplace transform consists of using Eq. (65) together with the ε-algorithm. The values of c and L are chosen according to the criteria outlined Honig and Hirdes[24].
7. Numerical Results and Discussion
The analysis is conducted for a magnesium crystal-like material. Following reference[25], the values of physical constants areλ= 9.4x1010 Nm-2, μ=4.0x1010 Nm-2, k = 1.0x1010 Nm-2, ρ=1.74x103 gm/cm3, γ=0.779x10-9N, j=0.2x10-15 cm2,cE=1.04x103 kgm-3, K*=1.7x102 Jm-1s-1deg-1, To=298 K, ν = 3.68x106Nm-21deg-1, τo=0.02, no=0.05.we consider the following electric constants for our problemσo = 9.36x105Col2/Cal.cm.sec, Ho = 105 Col/cm.secThe computations are carried out for the non-dimensional time t=0.1, strip width a=0.9x103 and rotation Ω=2and on the surface plane z=0. The distribution of non-dimensional transverse displacement u, non-dimensional normal displacement w, non-dimensional normal force stress σzz, non- dimensional tangential couple stress mzy, non-dimensional temperature distribution T non-dimensional current density jx and jz non-dimensional distance x have been shown in Figs. 1–7.The solid line represent magneto-micropolar generalized thermoelastic with Hall current effect and rotating medium MMGT(HR) and large dashes line represent magneto-micropolar generalized thermoelastic with Hall current effect MMGT(H), while small dashes line represent magneto-micropolar generalized thermoelastic in rotating medium without Hall current effect MMGT(R). The dot line represent magneto-micropolar generalized thermoelastic without Hall current effect and rotating medium MMGT. Fig.1 Studying the effect of Hall parameter m on the temperature distribution against y for, from this figure we  | Figure 1. Variation of temperature with the Hall parameter m |
see that the all curves start from the same value 1 at x=0.0 then decreases till it tends to zero at x =2, we observe that from this figure the temperature T decrease in the case MMGT(HR) in comparison to curve MMGT(R), while increases in comparison to curves MMGT and MMGT(H). The effect of parameter m on the transverse displacement u is presented in Fig. 2.It is noticed that from the graphic representation of the transverse displacement that the values are oscillatory for all the cases in the whole range and the values of u remain higher near the boundary condition in magnitude for case MMGT(HR) as compared with the values for all cases and then increases. Fig. 3 describes the variations of the normal displacement w under the effect of all parameters, it is noticed that the normal displacement w records values lower in case MMGT(HR) as compared with the values for all cases. It is shown in Fig. 4 that the values of normal force stress for MMGT(H) and MMGT lie in a very short range. The variation for all cases being oscillatory in nature are comparable in magnitude and the magnitude of these oscillations decrease with increase in horizontal distance x. Fig. 5 shows that the Variation of couple stress myz decreases as m increases MMGT(HR). The figure indicate that myz records values higher in case MMGT(H) as compared with the values of case MMGT(R) and all cases oscillations about y-axes. 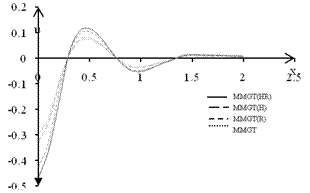 | Figure 2. Variation of transverse displacement with the Hall parameter m |
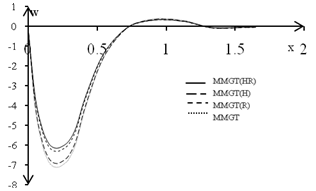 | Figure 3. Variation of normal displacement with the Hall parameter m |
 | Figure 4. Variation of normal force stress with the Hall parameter m |
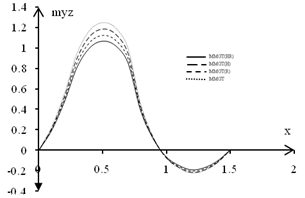 | Figure 5. Variation of couple stress with the Hall parameter m |
 | Figure 6. Variation of current density component Jx with the Hall parameter m |
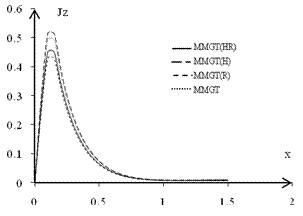 | Figure 7. Variation of current density component Jz with the Hall parameter m |
Figs. 6, 7 describe the variations of two components of density component Jx and Jz respectively, it is evident that the values of both fields are decreased in the MMGT(HR) as compared with the values for cases MMGT and MMGT(H).
References
| [1] | A. C. Eringen, E. S. Suhubi, Non-linear theory of micro-elastic Solids I. Int. J. Eng. Sci. 2(1964), 189–203 |
| [2] | E. S. Suhubi, A. C Eringen, Nonlinear theory of micro-elastic Solids II. Int. J. Eng. Sci. 2(1964), 389–404 |
| [3] | A. C. Eringen, A unified theory of thermo-mechanical materials, Int. J. Eng. Sci. 4(1966), 179–202 |
| [4] | A. C. Eringen, Linear theory of micropolar elasticity, ONR Technical Report No. 29, School of Aeronautics, Aeronautics and Engineering Science. Purdue University, (1965) |
| [5] | A. C. Eringen, Linear theory of micropolar elasticity, J. Mech. 15(1966), 909-923 |
| [6] | M. A. Biot, Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 27 (1956) 240–253 |
| [7] | H. Lord, Y. Shulman, A generalized dynamical theory of thermoelasticity, J. Mech. Phys. Solid 15 (1967) 299 |
| [8] | A. E. Green, K. A. Lindsay, Thermoelasticity. J. Elasticity 2 (1972), 1–7 |
| [9] | A. E. Green, N. Laws, On the entropy production inequality. Arch. Ration. Mech. Anal. 45(1972), 45–47 |
| [10] | Magdy A. Ezzat , Hamdy M. Youssef, Generalized magneto-thermoelasticity in a perfectly conducting medium, Int. J. Solids and Structures 42 (2005) 6319–6334 |
| [11] | L. Knopoff, The interaction between elastic wave motion and a magnetic field in electrical conductors. J. Geophys. Res. 60(1955), 441–456 |
| [12] | Chadwick, P., 1957. Ninth Int. Congr. Appl. Mech. 7, 143 |
| [13] | S. Kaliski, J. Petykiewicz, Equation of motion coupled with the field of temperature in a magnetic field involving mechanical and electrical relaxation for anisotropic bodies. Proc. Vibr. Probl. (1959)4, 1 |
| [14] | G. Paria, On magneto-thermoelastic plane waves. Proc. Cambr. Phil. Soc. 56 (1962), 527–531 |
| [15] | A. Wilson, Proc. Cambr. Phil. Soc. 59 (1963), 483–488 |
| [16] | G. Paria, Magneto-elasticity and magneto-thermoelasticity. Adv. Appl. Mech. 10 (1967), 73–112 |
| [17] | A. Nayfeh, S. Namat-Nasser, Electromagneto-thermoelastic plane waves in solids relaxation. J. Appl. Mech. E 39 (1972), 108–113 |
| [18] | S. Choudhuri, Electro-magneto-thermoelastic plane waves in rotating media with thermal relaxation. Int. J. Eng. Sci. 22 (1984), 519–530 |
| [19] | H. Sherief, M. Ezzat, A thermal sock problem in magneto-thermoelasticity with thermal relaxation. Int. J. Solids Struct. 33 (1996), 4449–4459 |
| [20] | Rajneesh Kumar, Effect of rotation in magneto-micropolar thermoelastic medium due to mechanical and thermal sources.Chaos, Solitons and Fractals in press |
| [21] | Rajneesh Kumar, Rupender , ManjeetSingh, Effect of rotation and imperfection on reflection and transmission of plane waves in anisotropic generalized thermoelastic media, J. Sound and Vibration, in press |
| [22] | Rajneesh Kumar, Praveen Ailawalia, Moving load response in micropolar thermoelastic medium without energy dissipation possessing cubic symmetry, International Journal of Solids and Structures 44 (2007) 4068–4078 |
| [23] | Moncef Aouadi, Temperature dependence of an elastic modulus in generalized linear micropolar thermoelasticity, ZAMP, .(2006) 1057{1074 |
| [24] | G. Honig, U. Hirdes: A method for the numerical inversion of Laplace transform. J. Comp. Appl. Math. 10 (1984) 113–132 |
| [25] | A. C. Eringen. Plane wave in nonlocal micropolar elasticity. Int J Eng Sci 22 (1984) 1113–1121 |


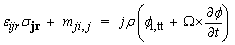
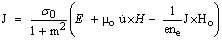
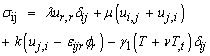

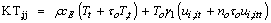
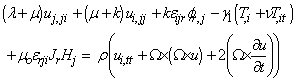
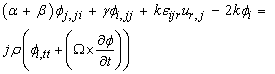
 0, ui = (u, 0, w), φi = (0, φ2, 0) and Ω = (0, Ω, 0), we also assume that E = 0, the generalized Ohm’s law gives Jy = 0 everywhere in the medium. The current density components Jx and Jz are given by:
0, ui = (u, 0, w), φi = (0, φ2, 0) and Ω = (0, Ω, 0), we also assume that E = 0, the generalized Ohm’s law gives Jy = 0 everywhere in the medium. The current density components Jx and Jz are given by: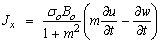
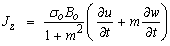
 where
where 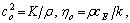 and M is the Hartmann number or magnetic parameter.The system of equations (6)-(8), using relations (9), and (10), takes the following form – dropping the asterisks for convenience-,
and M is the Hartmann number or magnetic parameter.The system of equations (6)-(8), using relations (9), and (10), takes the following form – dropping the asterisks for convenience-,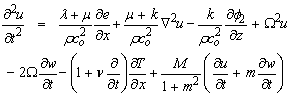
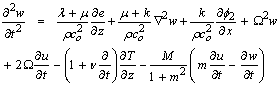

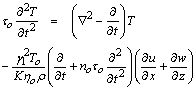
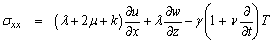




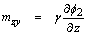


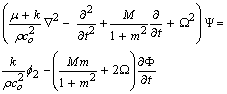

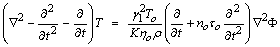
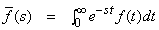 of both sides of (15)–(20) and (22)-(25) using the homogenous initial conditions, we obtain:
of both sides of (15)–(20) and (22)-(25) using the homogenous initial conditions, we obtain: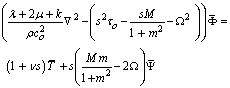
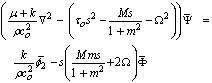

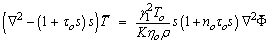
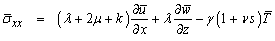
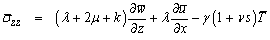
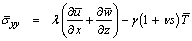
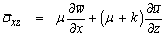
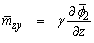
 Taking the Fourier transform of both sides of (26)–(33)
Taking the Fourier transform of both sides of (26)–(33)
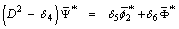
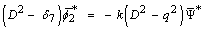

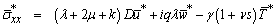



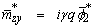

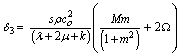
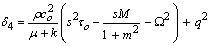
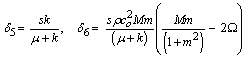
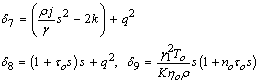 and the operator D means the derivative with respect to x.0n Eqs. (34)–(37) and after some simplification, we arrive at the followingeighth order differential equation satisfied by
and the operator D means the derivative with respect to x.0n Eqs. (34)–(37) and after some simplification, we arrive at the followingeighth order differential equation satisfied by 
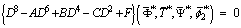



 The solution of the Eq. (44) satisfying the radiation conditions that
The solution of the Eq. (44) satisfying the radiation conditions that 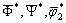 and
and 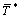 tend to zero as x tends to infinity can be written as
tend to zero as x tends to infinity can be written as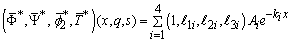
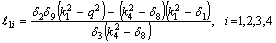
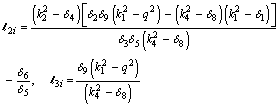 and ki (i=1,2,3,4) are the characteristic roots of the characteristic equation (36) which is
and ki (i=1,2,3,4) are the characteristic roots of the characteristic equation (36) which is Eq. (21) together with Eq. (45), immediately give
Eq. (21) together with Eq. (45), immediately give


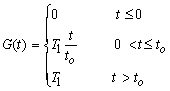

 We assume that, on the boundary x = 0 the displacement u of the body does not depends on x, hence we have Du(0, z, t) = 0 and the medium is subjected to a rough and rigid foundation enough to prevent the displacement w at any time and any point of z, so also we have w(0, x, t) = 0, mzy = 0.Applying the Laplace and Fourier transforms, we get
We assume that, on the boundary x = 0 the displacement u of the body does not depends on x, hence we have Du(0, z, t) = 0 and the medium is subjected to a rough and rigid foundation enough to prevent the displacement w at any time and any point of z, so also we have w(0, x, t) = 0, mzy = 0.Applying the Laplace and Fourier transforms, we get
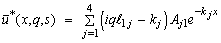
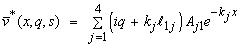
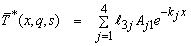
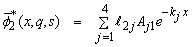
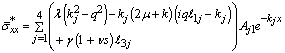
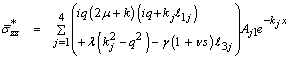


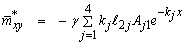

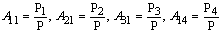



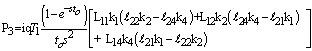


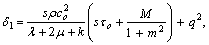
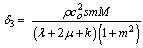
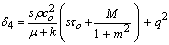
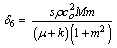 iv. Taking n0 =1, τo > 0, ν = 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for L–S theory.v. Taking n0 = 0, τo > 0, ν > 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for G–L theory.vi. Taking, n0 = 0, τo= 0, ν= 0 we obtain the corresponding expressions for magneto-micropolar coupled thermoelastic with rotating medium for (C–T theory
iv. Taking n0 =1, τo > 0, ν = 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for L–S theory.v. Taking n0 = 0, τo > 0, ν > 0 in Eqs. (52)–(61), we obtain the corresponding expressions for magneto-micropolar thermoelastic with rotating for G–L theory.vi. Taking, n0 = 0, τo= 0, ν= 0 we obtain the corresponding expressions for magneto-micropolar coupled thermoelastic with rotating medium for (C–T theory .First, we invert the Fourier transform using the inversion formula given previously. This gives the Laplace transform expression
.First, we invert the Fourier transform using the inversion formula given previously. This gives the Laplace transform expression 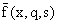 of the function f(x,y, t) as
of the function f(x,y, t) as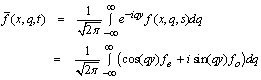 where fe and fo denote the even and the odd parts of the function
where fe and fo denote the even and the odd parts of the function 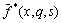 respectively.We shall now outline the numerical inversion method used to find the solution in the physical domain. For fixed values of x, y, and q the function inside braces in the last integral can be considered as a Laplace transform
respectively.We shall now outline the numerical inversion method used to find the solution in the physical domain. For fixed values of x, y, and q the function inside braces in the last integral can be considered as a Laplace transform  of some function g(t).The inversion formula for the Laplace transform can be written as
of some function g(t).The inversion formula for the Laplace transform can be written as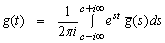 where c is an arbitrary real number greater than all the parts of the singularities
where c is an arbitrary real number greater than all the parts of the singularities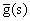 . Taking s = c + iy, the above integral takes the form
. Taking s = c + iy, the above integral takes the form Expanding the function h(t) = exp(-ct)g(t) in a Fourier series in the interval[0, 2L], we obtain the approximate formula.
Expanding the function h(t) = exp(-ct)g(t) in a Fourier series in the interval[0, 2L], we obtain the approximate formula.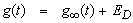 where
where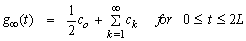
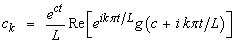
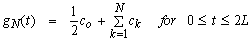
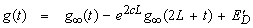 where the discretization error
where the discretization error 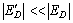 . Thus, the approximate value of g(t) becomes
. Thus, the approximate value of g(t) becomes
 be the sequence of partial sums of Eq. (64). We define the e-sequence by
be the sequence of partial sums of Eq. (64). We define the e-sequence by and
and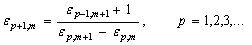 it can be shown that the sequence ε1,1, ε3,1, ε5,1, . . . , εN,1, converges to f(x,y, t) + ED – co/2 faster than the sequence of partial sums sm (m = 1,2,3,. . .).The actual procedure used to invert the Laplace transform consists of using Eq. (65) together with the ε-algorithm. The values of c and L are chosen according to the criteria outlined Honig and Hirdes[24].
it can be shown that the sequence ε1,1, ε3,1, ε5,1, . . . , εN,1, converges to f(x,y, t) + ED – co/2 faster than the sequence of partial sums sm (m = 1,2,3,. . .).The actual procedure used to invert the Laplace transform consists of using Eq. (65) together with the ε-algorithm. The values of c and L are chosen according to the criteria outlined Honig and Hirdes[24].






 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML