P Kishore Kumar , T Kishore kumar
Department of Electronics & Communication Engineering, National Institute of Technology, Warangal, 506 004, India
Correspondence to: P Kishore Kumar , Department of Electronics & Communication Engineering, National Institute of Technology, Warangal, 506 004, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Ultra-Wideband (UWB) is the promising technology for localization of the objects behind the walls. Recent terrorist activities and law-enforcement situations underscore the need for effective through-wall detection. UWB radar signals has extremely large frequency spectrum and since low frequencies has more penetration capabilities through dielectric materials it is best suitable for Through-the-Wall Radar Imaging (TWRI). Signal processing in TWRI has a greater impact in getting the information of the scanned area. This paper uses impulse signals in TWRI, examines the factors impacting in TWRI and obtains the two dimensional information of the scanned scene. Electromagnetic simulation software is used to generate the room like structure, and to obtain the raw radar data.
Keywords:
Ultra-Wideband, Impulse signal, Through-the-wall, Synthetic Aperture
Cite this paper: P Kishore Kumar , T Kishore kumar , UWB Impulse Radar for Through-The-Wall Imaging, International Journal of Electromagnetics and Applications, Vol. 1 No. 1, 2011, pp. 19-23. doi: 10.5923/j.ijea.20110101.05.
1. Introduction
The field of remote sensing has developed a range of interesting imaging approaches for a variety of applications. Through-the-wall and through-the-building sensing are relatively new areas that address the desire to see inside structures to determine the layout of buildings, where occupants may be, and even identify materials within the building. Through-wall sensing is highly desired by police, fire and rescue, emergency relief workers, and military operations. Accurate sensing and imaging can allow a police force to obtain an accurate description of a building in a hostage crisis, or allow fire fighters to locate people trapped inside a burning building. The goals of through-the-wall sensing technology are to provide vision into otherwise obscured areas.Each remote-sensing application area has driven different sensing modalities and imaging algorithm development based upon propagation characteristics, sensor positioning, and safety issues. Traditional optical, radar, and sonar image processing all begin with basic wave physics equations to provide focusing to individual points. In many radar applications, for example, data sampled from many sensors are mathematically integrated to provide equivalent focusing using free-space propagation assumptions. Free-space imaging is commonly seen in synthetic aperture radar (SAR) techniques [1] since atmospheric distortions are often negligible and can be safely ignored in first-order calculations.Free-space propagation does not apply for many interesting applications like geophysical sensing, medicalimaging, and more recently through building sensing where transmission through scattering media is encountered. In these applications, propagated signals diffract through a volume. As examples, geophysical imaging techniques generally measure seismic propagation through the earth to look for discontinuities that are often indicators of oil, gas, water, or mineral deposits. In medical imaging, ultrasound tomography approaches account for propagation through different tissue classes [2].Non-free-space scattering applications are more representative of the through-building sensing problem, albeit each has its own distinct challenges and approaches. In through-building sensing, there are many air–material interfaces that dramatically change the wave front. Through building sensors may be located some distance away from the structure and attenuation is largely seen only in the building materials and contents rather than in the large volumes of air that occupy most of the space within a building. Sensor standoff provides unique opportunities and challenges for exploiting building-dependent features. The paper is organized as follows. Section II describes the measurement scenario used in this paper and its specifications. In section III the effect of crosstalk and rage gating in TWRI is described. Back Projection algorithm is explained in section IV. Section V is devoted to results and Section VI for conclusion.
2. Measurement Scenario
A simplified sketch of the measurement layout is shown in fig 1. The radar system was horizontally scanned parallel to the front brick wall at a distance of 43.75 cm from the wall as shown in figure. The wall is considered as the brick wall and the specifications are given in table 1.The area that is scanned behind the wall covers the volume of 800 cm×700 cm×500 cm indicates length, width and height respectively. The transmitting and the receiving antennas are placed at the same position, keeping in view to make use of the same antenna for both transmitting and receiving for further studies.| Table 1. Electrical Parameters of the brick wall |
| | Type of wall | Brick wall | | Relative Permittivity | 4.440 | | Conductivity | 0.001 S/m | | Thickness of the wall | 0.125 m |
|
|
The objects that were placed behind the wall consists a wooden table on which an iron cylinder is placed and at other position a glass cylinder is placed. The specifications of the wooden table, iron cylinder and glass cylinder are given in table 2.Table 2 (a). Wooden table Properties
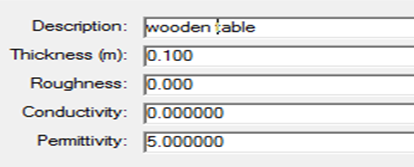 |
| |
|
Table 2(b). Glass Cylinder Properties
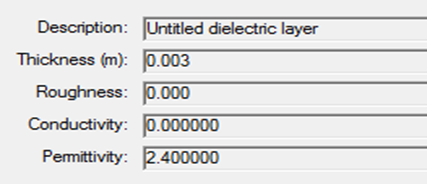 |
| |
|
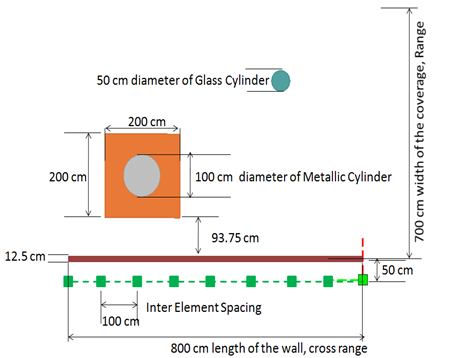 | Figure 1. Top view of the simulated measurement scenario |
One reason of selecting these materials (wood, metal and glass) is to check how the reflection of the signals takes place, and the second is these materials usually found in any rooms.Since Ultra-Wideband (UWB) signals has the better penetration properties and has the capability of obtaining high resolution images, we use an impulse signals particularly Gaussian derivative is used. 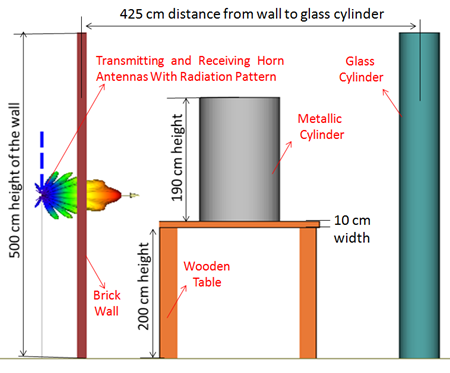 | Figure 2. Side view of the simulated measurement scenario |
The resolution is proportion to the bandwidth of the signal [3], [4] and is given by 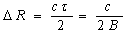 | (1) |
Where ΔR: Range Resolutionτ: Pulse WidthB: Bandwidth and c = 3×108 m/sec is the velocity of light in free space.The reason of selecting Gaussian doublet or the second derivative of the Gaussian pulse for transmitting is that it has only one peak which can be easily noticed in the time domain and also has the longest lobe in the frequency domain, creating the large bandwidth of the signal. Another pulse would not fit these requirements since it would not have both the large single pulse in the time domain and cover a large spectrum in the frequency domain [5], [6], [7].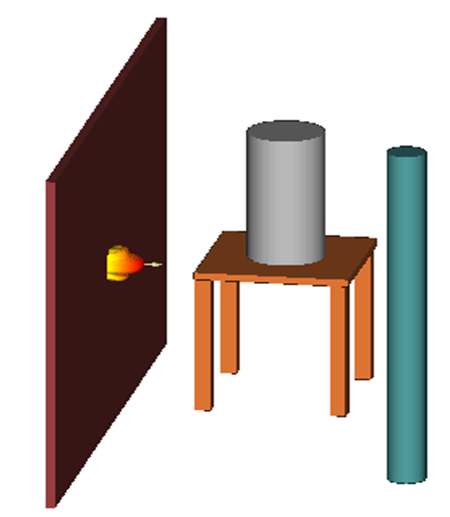 | Figure 3. Orthographic View |
Since the signal transmitted by the antenna is the derivative of the input signal, to make use of Gaussian doublet Gaussian first derivative is given as input signal to the antenna. The expressions for Gaussian pulse and its derivatives (up to second order derivative) are given by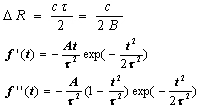 (2)The signal that was used here has the pulse width of 0.5 n sec and the with centre frequency of 1.83 GHz and 3.3 GHz bandwidth. The plot of the Gaussian derivative and its spectrum is shown in figure 3.
(2)The signal that was used here has the pulse width of 0.5 n sec and the with centre frequency of 1.83 GHz and 3.3 GHz bandwidth. The plot of the Gaussian derivative and its spectrum is shown in figure 3. 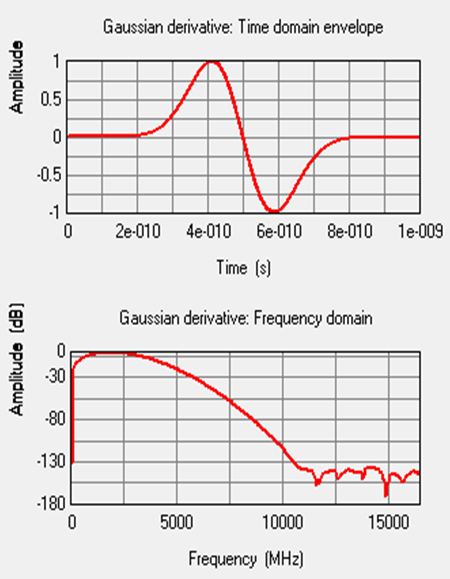 | Figure 4. (a) Gaussian Derivative (b) Its frequency Spectrum |
 Horn antennas were used for transmission and reception. Selecting horn antenna enhances the gain in the direction of scanning and to not to considering the region behind the antenna which is of no use. The horn antenna radiation pattern is shown in figure 5.
Horn antennas were used for transmission and reception. Selecting horn antenna enhances the gain in the direction of scanning and to not to considering the region behind the antenna which is of no use. The horn antenna radiation pattern is shown in figure 5.
3. Effect of Antenna Crosstalk and Range Gating in TWRI
Crosstalk is the part of the signal that travels directly between the transmitting and receiving antennas. It is the first and often the largest peak in the A-scan signal which affects the mean value of the signal. This signal constantly presents in all the measurements and contains no information of the scanned scene. Sometimes this largest peak signal may cross the maximum current rating of the receiver circuit over which the performance may be degraded 8. Hence it is very important to remove the crosstalk. The crosstalk can be obtained by measuring with radar in the free space, or with absorbers around (anechoic chamber). 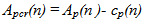 | (3) |
Where Ap(n) and cp(n) are the A-scan signal and crosstalk at pth position of an antenna respectively and Apcr(n) represents the A-scan signal at pth position with crosstalk removed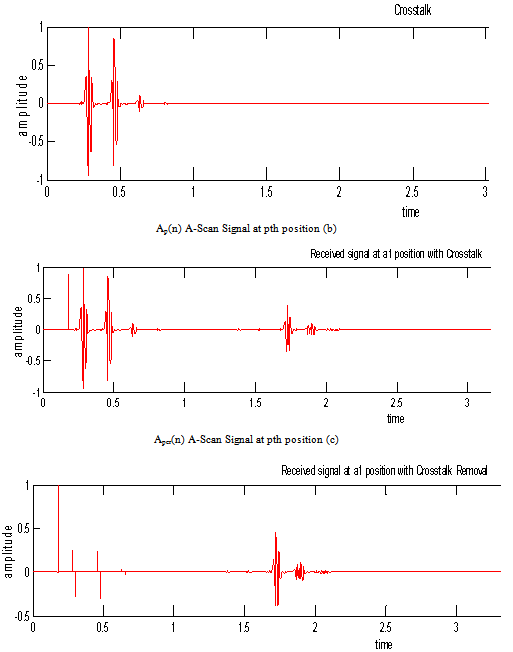 | Figure 6. (a) Crosstalk Measurement, (b) Received A-scan signal (c) A-scan signal after removing the crosstalk |
Range Gating is the basic preprocessing technique that decides to fix the maximum range of the scanned area. The receiver is made to switch on up to the delay that was fixed by the maximum range. After that delay the signal is assumed to be of even farther distance and hence ignored. The delay that was obtained for 500cm range is 0.466×10-9 sec. Since the velocity inside the wall is gets reduced by a factor of  the delay was increased to 0.55×10-9 sec which occurs at the index of 110000th sample.
the delay was increased to 0.55×10-9 sec which occurs at the index of 110000th sample.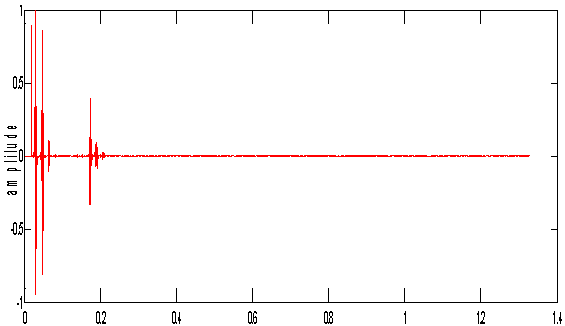 | Figure 7(a). A-scan signal without Range gating |
4. Back Projection Algorithm
The heading of the References section must not be numbered. This algorithm retrieves the image of the scanned area by making use of the A-scan signals at different receiver positions. Since the image is of 2D and is represented by an M×N matrix, the aim is obtain the corresponding numerical values to fill the matrix, such that the formed image should represent the scanned scene. Each numerical value in the M×N matrix represents a pixel value of an image. This image or 2D signal is also called as B-scan signal [11].The numerical value at any pixel position should be the contribution of the A-scan signals at all receiver positions. Since the range is fixed to 700 cm and the number of pixels in the range direction is N (N represents cross range and M represents the range), the range bins are selected such that the maximum range should not cross the prescribed value.The A-scan signal received at each receiver position assuming P targets in the region is represented as [9],[10].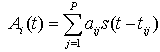 | (4) |
Where Ai(t) is the A-scan signal at ith receiver position, aij is the reflection coefficient of the jth tatget and tij is the delay of the signal from ith transmitter position to jth tatget position and to ith receiver position and is given by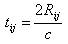 | (5) |
where Rij is the distance from ith transmitter position to the jth target position.A weight factor also should be there in eq (4) representing the attenuation of the signal. Similarly a term should be added in eq (5) representing the reduction of velocity inside the wall. Since the intention is to obtain the image, these terms are given little importance in this paper. The point spread response (PSR) which represents the spreading of signal energy in two dimensional space of a given A-scan signal is given by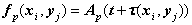 | (6) |
where i= 0,1,2,3…..M, j=0,1,2,3……N, xi, yj represents the pixel co-ordinatesand 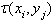 is the focusing delay [9] in the image space. The PSR at pth receiver position is shown in figure 8
is the focusing delay [9] in the image space. The PSR at pth receiver position is shown in figure 8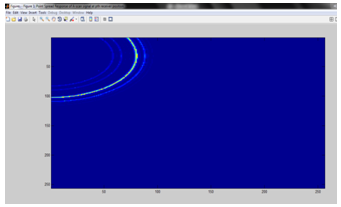 | Figure 8. Point Spread Response |
But the final image should have the contribution of all A-scan signals and hence all the PSR should be added. The expression is given by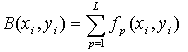 | (7) |
5. Results
Computer simulations implementing the impulse signals for through the wall imaging is done. The back projection algorithm is used to retrieve the image of the scanned region and the results obtained are shown in figure (9) and figure (10). The data collected from the receivers at different receiver positions is used in MATLAB to implement the algorithm. 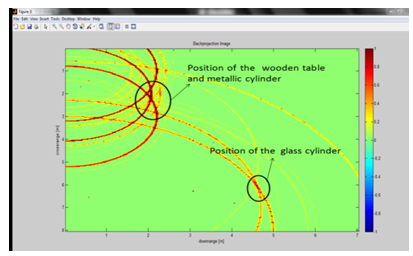 | Figure 9. Two dimensional image of the scene without wall indicating the position of the objects |
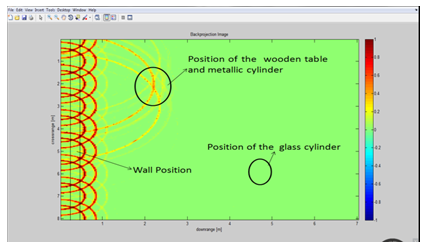 The Results clearly demonstrates the position of the objects that were there in the scanned region. The intersection point of the point spread responses obtained for different receiver position indicates the presence of the object.
The Results clearly demonstrates the position of the objects that were there in the scanned region. The intersection point of the point spread responses obtained for different receiver position indicates the presence of the object.
6. Conclusions
We have presented an approach of making use of impulse based signals for through the wall imaging. An electromagnetic simulation software is used to model the wall and objects inside the room. Three different materials were selected. The need for removing crosstalk and the necessasity of range gating is also explained. Finally Back projection algorithm is analyzed and used in retrieving the two dimensional image of the scanned region.
ACKNOWLEDGEMENTS
I wish to acknowledge my supervisor Dr. T. Kishore Kumar and Prof N. V. S. N Sarma for their support in this work.
References
| [1] | Giorgio Franceschetti, Riccardo Lanari, Synthetic Aperture Radar Processing, CRC Press, 1999. |
| [2] | A. C. Kak, M. Slaney, Principles of Computrized Tomographic Imaging, IEEE Press, New York, 1988. |
| [3] | James D. Taylor, “Ultra-Wide Band Radar Technology” ,CRC Press, 2001 |
| [4] | Taylor, J. D,: Introduction to Ultra-wideband radar systems. CRC Press, Boca Raton, FL |
| [5] | M. Ambors, “Ultra-Wideband Radar “seeing” Through Walls”, May 2007 |
| [6] | Ahmad Safaai-Jazi, Sedki M. Riad, Ali Muqaibel, and Ahmet Bayram, “Ultra-wideband Propagation Measurements and Channel Modeling” DARPA NETEX Program Report, November 18, 2002. |
| [7] | Sylvain Gauthier and Walid Chamma, “Through–The–Wall Surveillance” Technical Memorandum, DRDC Ottawa, October 2002. |
| [8] | Michal Aftanas “Through the wall imaging using M-sequence UWB radar system” a doctoral thesis, Slovak. Republic. December 2007. |
| [9] | Greg Barrie, “Ultra-wideband Synthetic Aperture” Data and image processing Technical Memorandum, DRDC Ottawa, January 2003. |
| [10] | N.T. Thanh, L. van Kempen, T.G. Savelyev, X. Zhuge, M. Aftanas, E. Zaikov, M. Drutarovsky, H. Sahli, “Comparision of Basic Inversion Techniques for Through-Wall Imaging Using UWB Radar”, Proceedings of 5th European Radar Conference, October 2008. |
| [11] | Fauzia Ahmad, Moeness G. Amin, Saleem & A. Kassam, “Synthetic Aperture Beamformer for Imaging Through a Dielectric Wall”, IEEE Transactions on Aerospace and Electronic Systems, Vol 41 No 1, 2005, 271-282. |



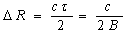

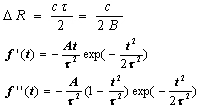 (2)The signal that was used here has the pulse width of 0.5 n sec and the with centre frequency of 1.83 GHz and 3.3 GHz bandwidth. The plot of the Gaussian derivative and its spectrum is shown in figure 3.
(2)The signal that was used here has the pulse width of 0.5 n sec and the with centre frequency of 1.83 GHz and 3.3 GHz bandwidth. The plot of the Gaussian derivative and its spectrum is shown in figure 3. 
 Horn antennas were used for transmission and reception. Selecting horn antenna enhances the gain in the direction of scanning and to not to considering the region behind the antenna which is of no use. The horn antenna radiation pattern is shown in figure 5.
Horn antennas were used for transmission and reception. Selecting horn antenna enhances the gain in the direction of scanning and to not to considering the region behind the antenna which is of no use. The horn antenna radiation pattern is shown in figure 5.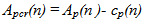

 the delay was increased to 0.55×10-9 sec which occurs at the index of 110000th sample.
the delay was increased to 0.55×10-9 sec which occurs at the index of 110000th sample.
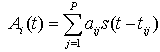
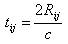
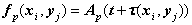
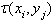 is the focusing delay [9] in the image space. The PSR at pth receiver position is shown in figure 8
is the focusing delay [9] in the image space. The PSR at pth receiver position is shown in figure 8
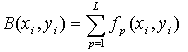

 The Results clearly demonstrates the position of the objects that were there in the scanned region. The intersection point of the point spread responses obtained for different receiver position indicates the presence of the object.
The Results clearly demonstrates the position of the objects that were there in the scanned region. The intersection point of the point spread responses obtained for different receiver position indicates the presence of the object.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
