Jiwei He1, 2
1School of International Trade and Economics, University of International Business and Economics, Beijing, 100029, China
2School of Mathematics and Physics, North China Electric Power University, Baoding 071003, China
Correspondence to: Jiwei He, School of International Trade and Economics, University of International Business and Economics, Beijing, 100029, China.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper studies the effects of pollution taxation on population in a polluted environment. We improve the classical Gallopin resource-consumer model, and assume that pollution taxation is imposed on toxicant emitters if the emission exceeds the amount permitted. We give some sufficient conditions under which the species in Gallopin system persists or becomes extinct. The threshold between persistence and extinction in some cases is obtained. We also verify these results with the help of numerical simulation.
Keywords:
Resource-consumer system, Pollution taxation, Persistence
Cite this paper: Jiwei He, Conservation of a Resource-Consumer Systemby Imposing Taxation on Pollution, International Journal of Ecosystem, Vol. 4 No. 4, 2014, pp. 197-202. doi: 10.5923/j.ije.20140404.06.
1. Introduction1
Uncontrolled contribution of toxicant to the environment has led many species to extinction and several others at the verge of extinction. It has been shown that toxicant can decrease the birth rate, increase the death rate and reduce the carrying capacity of the environment. One efficient way to control the environment pollution is imposing pollution taxation on toxicant emitters. In this paper, we introduce a mathematical model to analyze the effects of pollution taxation on Gallopin system in a polluted environment. The study of deterministic dynamic population models with toxicant effects was established by Hallam and his colleagues in the 1980s [1, 2, 3]. This model has been improved by many scholars [4, 5, 6]. Srinivasu [7] improved the model of Hallam by considering the direct effects of the toxicant in the environment on the population, and determined aclean-up policy to be implemented at the source of pollutants in order to conserve a population. He et al [8] studied the survival of a single species in the polluted environment, considering the organism’s uptake of toxicant from the environment and egestion of the internal toxicant to the environment. He and Ma [9] studied a Gallopin resource-consumer model, and obtained the threshold between the persistence and extinction of the consumer. Buonomo [10] et al studied the effects of variation of the population amount on the toxicant concentration in the organism and environment. He and Wang [11, 12] improved the ordinary differential equation system induced by Buonomo [10], and also applied to the Gallopin resource - consumer system. He [13] studied the effects of taxation on a single logistic species in the polluted environment. This paper improves the classical Gallopin resource - consumer system in a polluted environment, on the assumption of the living organisms absorbing part of the toxicant into their bodies so that the dynamics of the population is affected by this (internal) toxicant. It is assumed that pollution taxation is imposed on toxicant emitters if their emission exceeds the amount permitted by the government. This paper only discusses the conditions of the emission beyond the limit. It also considers the negative effects of taxation evasion. The sufficient conditions for persistence or extinction of the population are obtained, and some numerical simulation is given.
2. The Model
The study is relied on the hypothesis of a complete spatial homogeneous environment without migration. Let 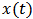 represent the population of the consumer species at time
represent the population of the consumer species at time 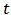 ,
, 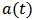 denote the quantity of the resources at time
denote the quantity of the resources at time 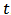 ,
, 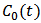 be the toxicant concentration in a body,
be the toxicant concentration in a body, 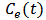 be the toxicant concentration of the environment at time
be the toxicant concentration of the environment at time 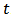 , and
, and 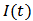 be the pollution taxation imposed on the emitters. A single species resource-consumer model of Gallopin system [9, 14, 15] in a polluted environment is improved as follows
be the pollution taxation imposed on the emitters. A single species resource-consumer model of Gallopin system [9, 14, 15] in a polluted environment is improved as follows 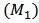 :
: 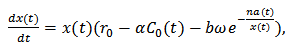 | (1) |
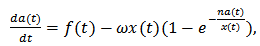 | (2) |
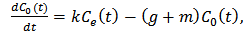 | (3) |
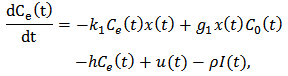 | (4) |
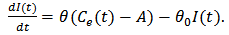 | (5) |
In this model, 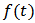 is the continuous growth rate of the resource in the absence of the consumer.
is the continuous growth rate of the resource in the absence of the consumer. 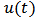 , the exogenous toxicant input rate, defined on
, the exogenous toxicant input rate, defined on 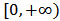 , is a bounded non-negativecontinuous function, and
, is a bounded non-negativecontinuous function, and 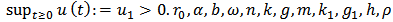 are positive constants.
are positive constants. 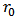 is the intrinsic growth rate of the species in the absence of the toxicant in the environment.
is the intrinsic growth rate of the species in the absence of the toxicant in the environment. 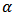 represents the species response to the toxicant present in the organism.
represents the species response to the toxicant present in the organism. 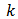 denotes an organism’s net uptake rate of the toxicant from the environment.
denotes an organism’s net uptake rate of the toxicant from the environment. 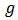 and m represent the egestion and deputation rates of the toxicant in an organism. The constant
and m represent the egestion and deputation rates of the toxicant in an organism. The constant 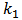 is given by
is given by 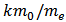 , where
, where 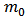 and
and 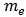 represent the average mass of an individual in the population and the total mass of the medium in the environment, respectively. Similarly
represent the average mass of an individual in the population and the total mass of the medium in the environment, respectively. Similarly 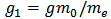 .
. 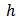 denotes the loss rate of the toxicant in the environment due to natural degradation.
denotes the loss rate of the toxicant in the environment due to natural degradation. 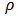 is the taxation repulsion coefficient.
is the taxation repulsion coefficient. 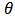 is the coefficient of the taxation imposed on the emitters. Taxation is imposed only if
is the coefficient of the taxation imposed on the emitters. Taxation is imposed only if 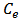 exceeds the permitted limit
exceeds the permitted limit 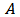 (For convenience sake, we assume
(For convenience sake, we assume 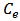 always exceeds
always exceeds 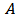 , the limit is up to which there is bare harm to the population.).
, the limit is up to which there is bare harm to the population.). 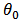 denotes some practical difficulties(such as tax evasion) on implementing the tax system. The initial values are
denotes some practical difficulties(such as tax evasion) on implementing the tax system. The initial values are 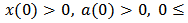
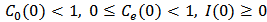 .Some notations defined:
.Some notations defined: 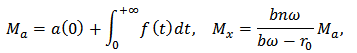
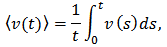
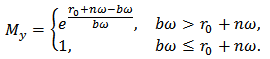 Definition 1. A population
Definition 1. A population 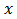 is said to be weakly persistent if
is said to be weakly persistent if 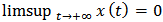 ; it goes to extinction if
; it goes to extinction if 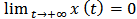 .We have the following lemmas similar to lemma 1 and lemma 2 in Ref. 9. Lemma 1. For model
.We have the following lemmas similar to lemma 1 and lemma 2 in Ref. 9. Lemma 1. For model 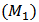 , the field
, the field 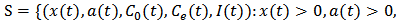
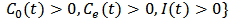 is an invariant set.Lemma 1 shows that if the initial values of model (M1) are in set S, then the solutions are always in S.Both
is an invariant set.Lemma 1 shows that if the initial values of model (M1) are in set S, then the solutions are always in S.Both 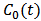 and
and 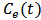 in model (M1) are concentrations of the toxicant, so the inequalities
in model (M1) are concentrations of the toxicant, so the inequalities 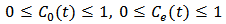 must be satisfied to be realistic. These limitations should be reflected in some conditions among the coefficients of model (M1). These conditions are shown in the following lemma.Lemma 2. For model
must be satisfied to be realistic. These limitations should be reflected in some conditions among the coefficients of model (M1). These conditions are shown in the following lemma.Lemma 2. For model 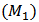 , if
, if 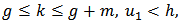 then
then 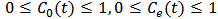 for all
for all 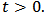 If the continuous growth rate of the resourcesatisfies some conditions, then the amount of the resource, population and pollution taxation must be limited.Lemma 3. For model
If the continuous growth rate of the resourcesatisfies some conditions, then the amount of the resource, population and pollution taxation must be limited.Lemma 3. For model 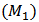 , if
, if 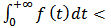
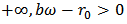 , then
, then 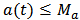 ,
, 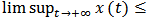
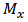 and
and 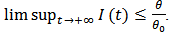 Proof. Equation (2) means
Proof. Equation (2) means 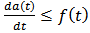 . Then
. Then 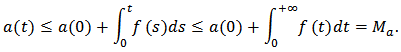 From equation (1), we have
From equation (1), we have 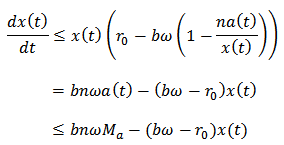 Based on the standard comparison theorem, we get
Based on the standard comparison theorem, we get 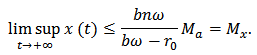 Analogously, from equation (5) we obtain
Analogously, from equation (5) we obtain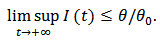
3. Main Results
The problem we are interested in is to find the conditions under which the population in model 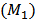 is persistent or goes to extinction.Theorem 1. For model
is persistent or goes to extinction.Theorem 1. For model 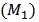 , if
, if 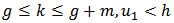 and
and 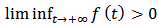 ,
, 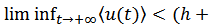
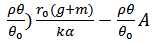 , then the population
, then the population 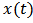 will be weakly persistent.Proof. If the conclusion of theorem is false, i.e.
will be weakly persistent.Proof. If the conclusion of theorem is false, i.e. 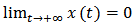 , there will be a contradiction. Firstly, we will show that
, there will be a contradiction. Firstly, we will show that 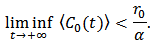 Equations (3), (4) and (5) can be rewritten as:
Equations (3), (4) and (5) can be rewritten as: 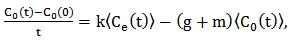 | (6) |
 | (7) |
 | (8) |
Since  and
and  are bounded, then
are bounded, then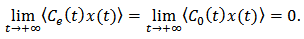 From expression (6) (7) and (8), we can obtain that
From expression (6) (7) and (8), we can obtain that 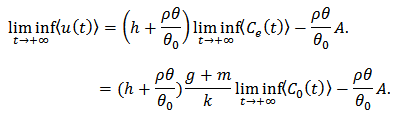 Then
Then 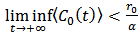 follows immediately according to the conditions of the theorem. Since
follows immediately according to the conditions of the theorem. Since 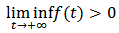 , there exist
, there exist 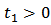 and
and 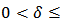
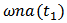 such that
such that 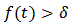 for
for 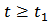 . Taylor’s theorem enables us to write
. Taylor’s theorem enables us to write 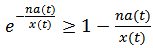 . Then from equation (2) we have
. Then from equation (2) we have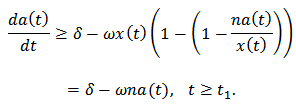 The solution of the differential equation
The solution of the differential equation 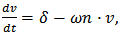 starting from
starting from 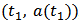 , is
, is 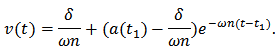 Then from a standard comparison theorem, we have
Then from a standard comparison theorem, we have 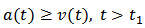 . Since
. Since 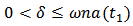 , then
, then 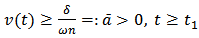 . That is
. That is 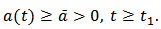 Then
Then 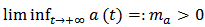 . For any
. For any 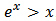 , then
, then 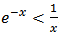 . So equation (1) implies that
. So equation (1) implies that 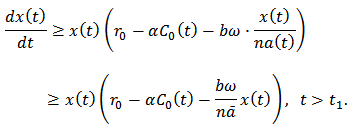 Dividing this inequality by
Dividing this inequality by 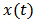 and then integrating it from
and then integrating it from 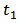 to
to 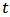 , we can get that
, we can get that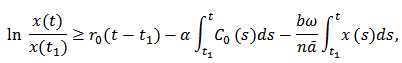
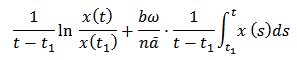
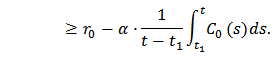 Then we take the upper limit on both sides of the last inequality,
Then we take the upper limit on both sides of the last inequality, 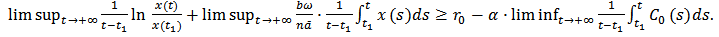 | (9) |
The following expression is obvious to be obtained: 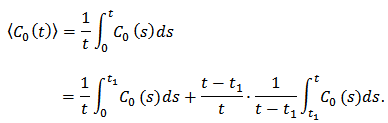 Which leads to
Which leads to 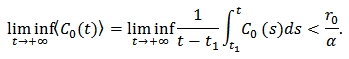 The assumption
The assumption 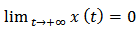 gives that
gives that 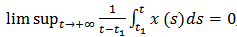 , then by inequality (9), we have
, then by inequality (9), we have 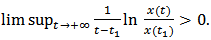 This is impossible. In fact, from the assumption
This is impossible. In fact, from the assumption 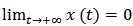 , we know that
, we know that 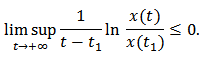 So the conclusion of theorem 1 is true. Theorem 2. For model
So the conclusion of theorem 1 is true. Theorem 2. For model 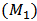 , if the conditions of lemmas 2 and 3 are satisfied and one of the following condition groups holds, then the population will go to local extinction.
, if the conditions of lemmas 2 and 3 are satisfied and one of the following condition groups holds, then the population will go to local extinction.  where
where 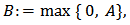
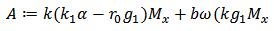
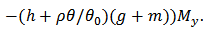 Proof. Assume that
Proof. Assume that 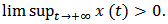 From equation (1), we can get that
From equation (1), we can get that 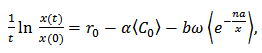 | (10) |
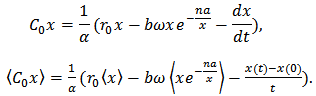 | (11) |
From (8), we have 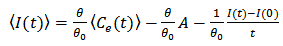 | (12) |
Substitution of (11), (12) into (7) gives 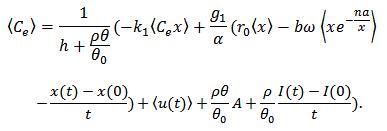 Equation (6) implies that
Equation (6) implies that 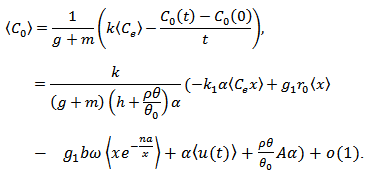 | (13) |
Here 0(1) is an infinitesimal, that is to say its limitation is 0 as t tends to infinity. Substituting into (10), we get 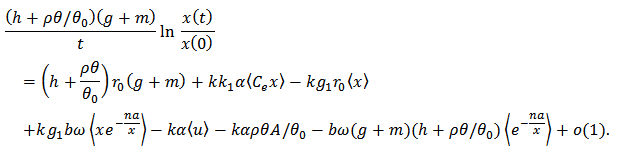 By the use of
By the use of 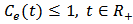 , the above expression can be rewritten as
, the above expression can be rewritten as 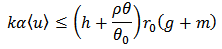
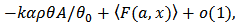 where
where 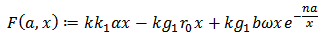
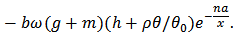 Therefore
Therefore 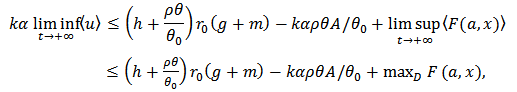 | (14) |
where 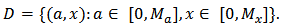 Let
Let 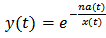 . Define
. Define 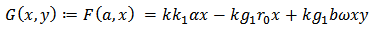
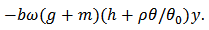 Now we want to know the range of y(t). Using equations (1) and (2),
Now we want to know the range of y(t). Using equations (1) and (2), 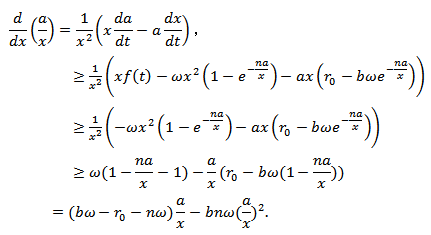 If
If 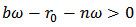 , then the standard comparison theorem results in
, then the standard comparison theorem results in 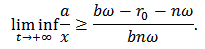 If
If 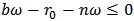 , then at least
, then at least 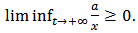 According to the meaning of
According to the meaning of 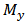 , we have
, we have 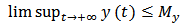 . Thus
. Thus 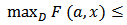
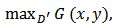 where
where 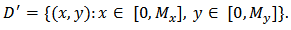 Let
Let 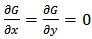 . We get
. We get 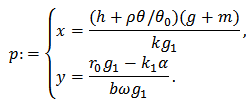 Since
Since 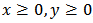 , then
, then 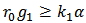 . The value of
. The value of 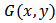 at point p gives
at point p gives 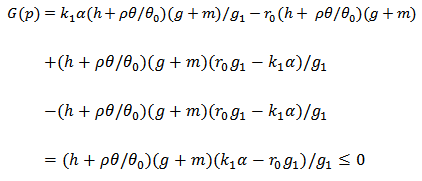 Since
Since 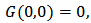 we can assert that
we can assert that 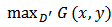 must be taken on the boundary of
must be taken on the boundary of 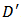 . When
. When 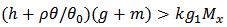 and
and 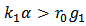 , then
, then 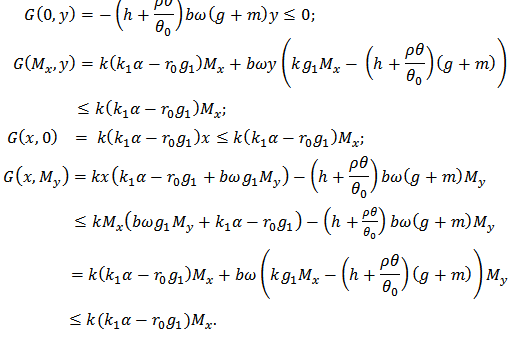 So
So 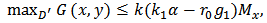 and since
and since 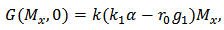 then
then 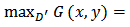
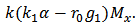 Similarly, when
Similarly, when 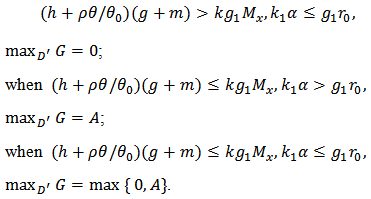 Using inequality (14), it contradicts with the conditions of theorem 2 accordingly.
Using inequality (14), it contradicts with the conditions of theorem 2 accordingly.
4. Numerical Simulation
The relations obtained from the theorems are well consistent with the actual data observed. In application of MATLAB software package, graphs are plotted for different values obtained in order to confirm the conclusion we have acquired above. Set 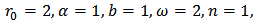
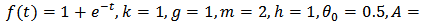
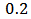 , and the initial values are
, and the initial values are 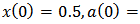
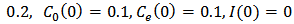 . The following Figure 1 describes the behavior of the population for different exogenous toxicant input rate u in the absence of pollution taxation, Figure 2 shows the behavior of the population in the presence and absence of pollution taxation.
. The following Figure 1 describes the behavior of the population for different exogenous toxicant input rate u in the absence of pollution taxation, Figure 2 shows the behavior of the population in the presence and absence of pollution taxation. 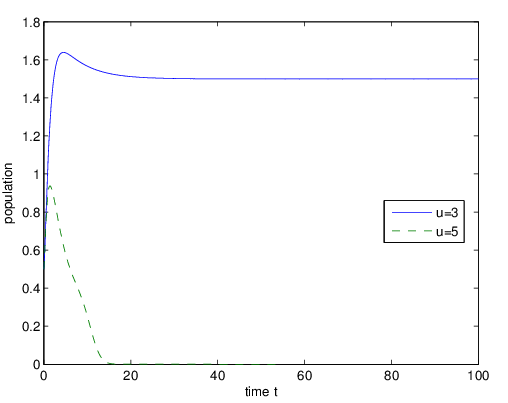 | Figure 1. The long behavior of population when 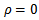 |
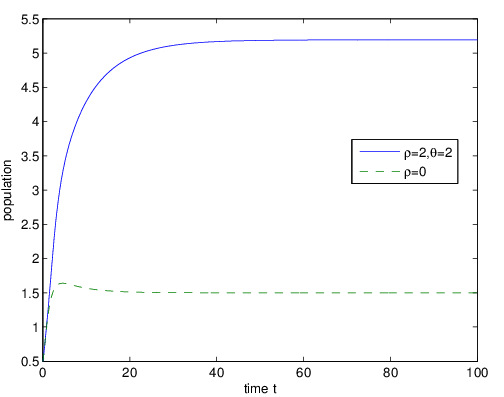 | Figure 2. The long behavior of population when 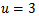 |
Figure 1 and Figure 2 show that the amount of the population decreases with the increase of the exogenous toxicant input rate, and even goes to extinction. However, when the pollution taxation is imposed on the toxicant emitters, the amount of the population increases to 5.25 from 1.5 rapidly.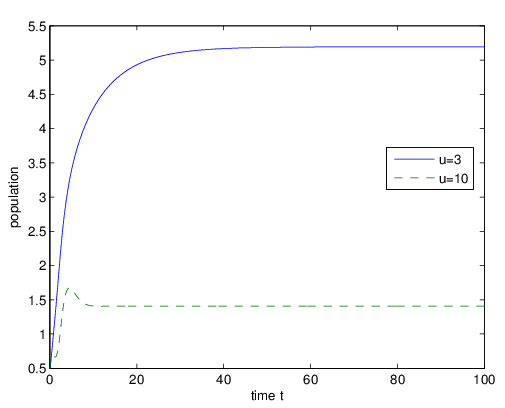 | Figure 3. The long behavior of population when 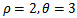 |
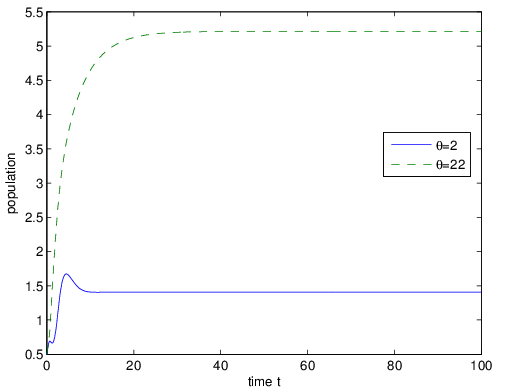 | Figure 4. The long behavior of population when 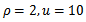 |
Figure 3 denotes the behavior of the population for different rate of emission of toxicant. We can observe that when u increases from 3 to 10, there will be a sharp decrease of the amount of the population. Nevertheless, when the heavy taxation 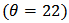 is imposed on the emitters, the balanced amount of the population will return to 5.25 from 1.4 quickly (Figure 4). The taxation coefficient
is imposed on the emitters, the balanced amount of the population will return to 5.25 from 1.4 quickly (Figure 4). The taxation coefficient 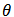 is the key parameter which needs to be chosen very carefully in order to maintain the equilibrium level of population.
is the key parameter which needs to be chosen very carefully in order to maintain the equilibrium level of population.
5. Conclusions
The main focus of this paper is to analyze the long behavior of Gallopin resource-consumer system, when the population is affected by toxicant emitted into the environment by external sources. It is further assumed that the cumulative rate of emission is reduced due to the levy of taxation. The model 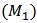 reduces to the system in [9] if there is no pollution taxation. Conditions which guarantee the persistence or extinction of the system are also given. The threshold between persistence and extinction is
reduces to the system in [9] if there is no pollution taxation. Conditions which guarantee the persistence or extinction of the system are also given. The threshold between persistence and extinction is 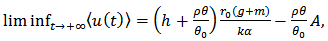 when the conditions of theorem 1 and (I) of theorem 2 are satisfied. In [9] this threshold is
when the conditions of theorem 1 and (I) of theorem 2 are satisfied. In [9] this threshold is 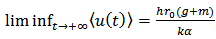 . By numerical simulation, it is shown that the amount of population decreases as the cumulative rate of the emission of the toxicant from external sources increases. So we need to control the emission rate of toxicant from external sources. Moreover, we note that when taxation are imposed on emitters of toxicant, the amount of population increases and shift more near to the level when the ecosystem is in the absence of toxicant.
. By numerical simulation, it is shown that the amount of population decreases as the cumulative rate of the emission of the toxicant from external sources increases. So we need to control the emission rate of toxicant from external sources. Moreover, we note that when taxation are imposed on emitters of toxicant, the amount of population increases and shift more near to the level when the ecosystem is in the absence of toxicant.
Note
1. Sponsored by “the Postgraduate Innovative Research Fund” of University of International Business and Economics (201310), the National Natural Science Foundation of China (71171052), the Fundamental Research Funds for the Central Universities (2014MS171).
References
| [1] | T. G. Hallam, C. E. Clark, R. R. Lassiter, 1983, Effects of toxicants on populations, A qualitative approach I: Equilibrium environmental exposure, Ecological Modelling, 18(3), 291-304. |
| [2] | T. G. Hallam, C. E. Clark, G. S. Jordan, 1983, Effects of toxicants on populations, A qualitative approach II: First order kinetics, Journal of Mathematical Biology, 18(1), 25-37. |
| [3] | T. G. Hallam, J. T. Luna, 1984, Effects of toxicants on populations, A qualitative approach III: Environmental and food chain pathways, Journal of Theoretical Biology, 109(3), 411-429. |
| [4] | L. Chen, Mathematical Models and Methods in Ecology, Chengdu, Sichuan Science Press, 2003. |
| [5] | Z. Ma, Mathematical Modeling and Study on Population Ecology, Hefei, Anhui Education Press, 1996. |
| [6] | J. B. Shukla, S. Sharma, B. Dubey, P. Sinha, 2009, Modeling the survival of resource-dependent population: Effects of toxicants (pollutants) emitted from external sources as well as formed by its precursors, Nonlinear Analysis: Real World Applications 10, 54-70. |
| [7] | P. D. N. Srinivasu, 2002, Control of environmental pollution to conserve a population, Nonlinear Analysis: Real World Applications, 3(3), 397-411. |
| [8] | Z. He, Z. Ma, 1997, The effects of toxicant and harvest on the logistic model, Journal of Biomathematics, 12(2), 230-237. |
| [9] | Z. He, Z. Ma, 2001, The survival analysis for Gallopin system in a polluted environment, Applied Mathematics and Mechanics, 21(8), 921-928. |
| [10] | B. Buonomo, A. D. Liddo, I. Sgura, 1999, A diffusiveconvective model for the dynamics of populationtoxicant intentions: some analytical and numerical results, Mathematical Biosciences, 157(1), 37-64. |
| [11] | J. He, K. Wang, 2009, The survival analysis for a population in a polluted environment, Nonlinear Analysis: Real World Applications, 10(3), 1555-1571. |
| [12] | J. He, K. Wang, 2007, The survival analysis for a single-species population model in a polluted environment, Applied Mathematical Modelling, 31(10), 2227-2238. |
| [13] | J. He, 2011, Effects of pollution tax on population in a polluted environment. Mathematical Methods in the Applied Sciences, 34, 1440-1444. |
| [14] | Z. Ma, B. Song, T. G. Hallam, 1989, The threshold between persistence and extinction of a population in a polluted environment, Bulletin of Mathematical Biology, 51, 311-323. |
| [15] | G. C. Gallopin, 1971, A generalized model of resource-population system: I. General properties. II. Stability analysis, Oecologia, 7, 382-432. |
 represent the population of the consumer species at time
represent the population of the consumer species at time 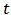 ,
, 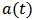 denote the quantity of the resources at time
denote the quantity of the resources at time 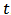 ,
, 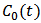 be the toxicant concentration in a body,
be the toxicant concentration in a body, 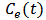 be the toxicant concentration of the environment at time
be the toxicant concentration of the environment at time 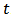 , and
, and 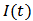 be the pollution taxation imposed on the emitters. A single species resource-consumer model of Gallopin system [9, 14, 15] in a polluted environment is improved as follows
be the pollution taxation imposed on the emitters. A single species resource-consumer model of Gallopin system [9, 14, 15] in a polluted environment is improved as follows 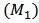 :
: 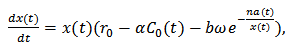
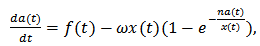
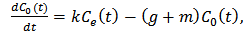
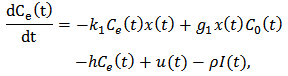
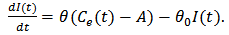
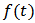 is the continuous growth rate of the resource in the absence of the consumer.
is the continuous growth rate of the resource in the absence of the consumer. 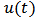 , the exogenous toxicant input rate, defined on
, the exogenous toxicant input rate, defined on 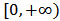 , is a bounded non-negativecontinuous function, and
, is a bounded non-negativecontinuous function, and 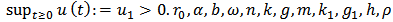 are positive constants.
are positive constants. 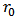 is the intrinsic growth rate of the species in the absence of the toxicant in the environment.
is the intrinsic growth rate of the species in the absence of the toxicant in the environment. 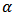 represents the species response to the toxicant present in the organism.
represents the species response to the toxicant present in the organism. 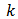 denotes an organism’s net uptake rate of the toxicant from the environment.
denotes an organism’s net uptake rate of the toxicant from the environment. 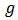 and m represent the egestion and deputation rates of the toxicant in an organism. The constant
and m represent the egestion and deputation rates of the toxicant in an organism. The constant 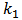 is given by
is given by 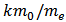 , where
, where 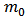 and
and 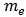 represent the average mass of an individual in the population and the total mass of the medium in the environment, respectively. Similarly
represent the average mass of an individual in the population and the total mass of the medium in the environment, respectively. Similarly 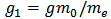 .
. 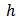 denotes the loss rate of the toxicant in the environment due to natural degradation.
denotes the loss rate of the toxicant in the environment due to natural degradation. 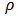 is the taxation repulsion coefficient.
is the taxation repulsion coefficient. 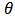 is the coefficient of the taxation imposed on the emitters. Taxation is imposed only if
is the coefficient of the taxation imposed on the emitters. Taxation is imposed only if 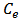 exceeds the permitted limit
exceeds the permitted limit 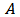 (For convenience sake, we assume
(For convenience sake, we assume 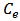 always exceeds
always exceeds 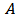 , the limit is up to which there is bare harm to the population.).
, the limit is up to which there is bare harm to the population.). 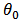 denotes some practical difficulties(such as tax evasion) on implementing the tax system. The initial values are
denotes some practical difficulties(such as tax evasion) on implementing the tax system. The initial values are 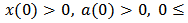
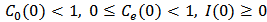 .Some notations defined:
.Some notations defined: 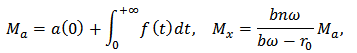
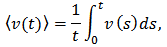
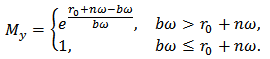 Definition 1. A population
Definition 1. A population 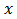 is said to be weakly persistent if
is said to be weakly persistent if 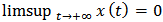 ; it goes to extinction if
; it goes to extinction if 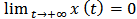 .We have the following lemmas similar to lemma 1 and lemma 2 in Ref. 9. Lemma 1. For model
.We have the following lemmas similar to lemma 1 and lemma 2 in Ref. 9. Lemma 1. For model 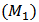 , the field
, the field 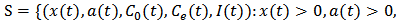
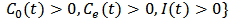 is an invariant set.Lemma 1 shows that if the initial values of model (M1) are in set S, then the solutions are always in S.Both
is an invariant set.Lemma 1 shows that if the initial values of model (M1) are in set S, then the solutions are always in S.Both 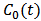 and
and 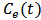 in model (M1) are concentrations of the toxicant, so the inequalities
in model (M1) are concentrations of the toxicant, so the inequalities 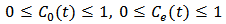 must be satisfied to be realistic. These limitations should be reflected in some conditions among the coefficients of model (M1). These conditions are shown in the following lemma.Lemma 2. For model
must be satisfied to be realistic. These limitations should be reflected in some conditions among the coefficients of model (M1). These conditions are shown in the following lemma.Lemma 2. For model 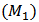 , if
, if 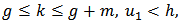 then
then 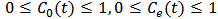 for all
for all 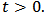 If the continuous growth rate of the resourcesatisfies some conditions, then the amount of the resource, population and pollution taxation must be limited.Lemma 3. For model
If the continuous growth rate of the resourcesatisfies some conditions, then the amount of the resource, population and pollution taxation must be limited.Lemma 3. For model 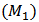 , if
, if 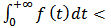
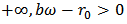 , then
, then 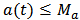 ,
, 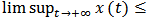
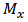 and
and 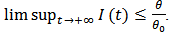 Proof. Equation (2) means
Proof. Equation (2) means 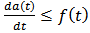 . Then
. Then 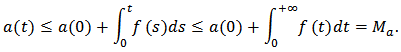 From equation (1), we have
From equation (1), we have 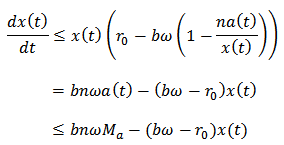 Based on the standard comparison theorem, we get
Based on the standard comparison theorem, we get 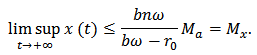 Analogously, from equation (5) we obtain
Analogously, from equation (5) we obtain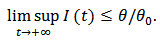
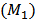 is persistent or goes to extinction.Theorem 1. For model
is persistent or goes to extinction.Theorem 1. For model 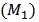 , if
, if 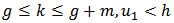 and
and 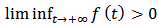 ,
, 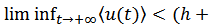
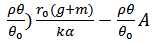 , then the population
, then the population 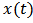 will be weakly persistent.Proof. If the conclusion of theorem is false, i.e.
will be weakly persistent.Proof. If the conclusion of theorem is false, i.e. 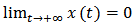 , there will be a contradiction. Firstly, we will show that
, there will be a contradiction. Firstly, we will show that 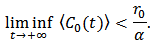 Equations (3), (4) and (5) can be rewritten as:
Equations (3), (4) and (5) can be rewritten as: 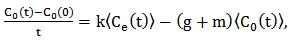
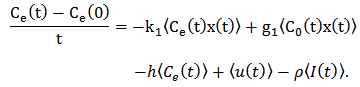
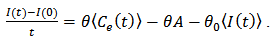
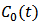 and
and 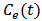 are bounded, then
are bounded, then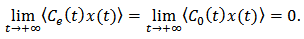 From expression (6) (7) and (8), we can obtain that
From expression (6) (7) and (8), we can obtain that 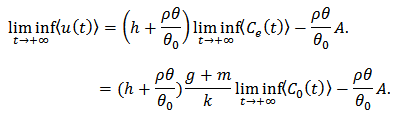 Then
Then 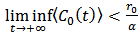 follows immediately according to the conditions of the theorem. Since
follows immediately according to the conditions of the theorem. Since 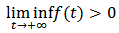 , there exist
, there exist 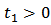 and
and 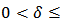
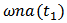 such that
such that 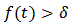 for
for 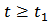 . Taylor’s theorem enables us to write
. Taylor’s theorem enables us to write 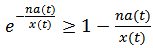 . Then from equation (2) we have
. Then from equation (2) we have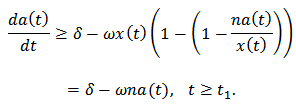 The solution of the differential equation
The solution of the differential equation 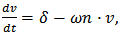 starting from
starting from 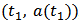 , is
, is 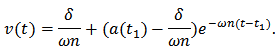 Then from a standard comparison theorem, we have
Then from a standard comparison theorem, we have 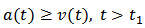 . Since
. Since 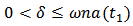 , then
, then 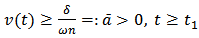 . That is
. That is 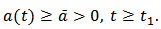 Then
Then 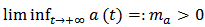 . For any
. For any 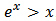 , then
, then 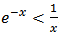 . So equation (1) implies that
. So equation (1) implies that 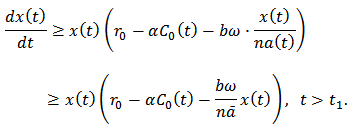 Dividing this inequality by
Dividing this inequality by 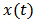 and then integrating it from
and then integrating it from 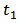 to
to 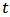 , we can get that
, we can get that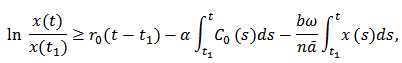
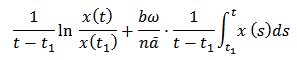
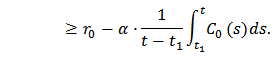 Then we take the upper limit on both sides of the last inequality,
Then we take the upper limit on both sides of the last inequality, 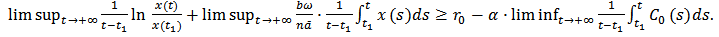
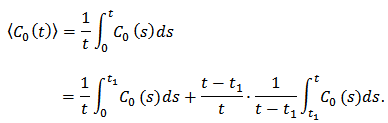 Which leads to
Which leads to 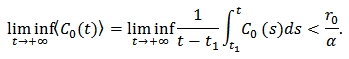 The assumption
The assumption 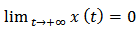 gives that
gives that 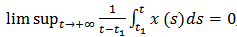 , then by inequality (9), we have
, then by inequality (9), we have 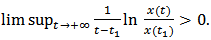 This is impossible. In fact, from the assumption
This is impossible. In fact, from the assumption 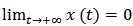 , we know that
, we know that 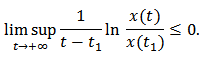 So the conclusion of theorem 1 is true. Theorem 2. For model
So the conclusion of theorem 1 is true. Theorem 2. For model 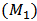 , if the conditions of lemmas 2 and 3 are satisfied and one of the following condition groups holds, then the population will go to local extinction.
, if the conditions of lemmas 2 and 3 are satisfied and one of the following condition groups holds, then the population will go to local extinction.  where
where 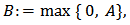
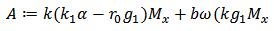
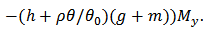 Proof. Assume that
Proof. Assume that 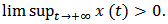 From equation (1), we can get that
From equation (1), we can get that 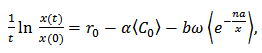
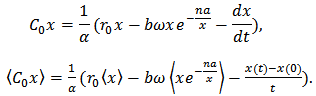
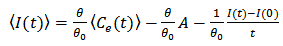
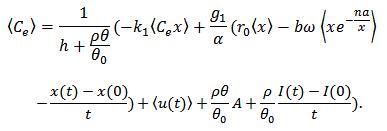 Equation (6) implies that
Equation (6) implies that 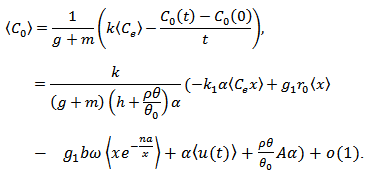
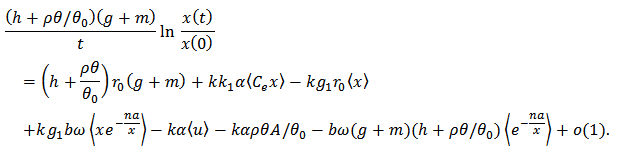 By the use of
By the use of 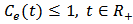 , the above expression can be rewritten as
, the above expression can be rewritten as 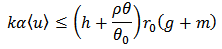
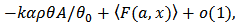 where
where 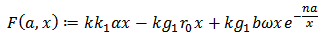
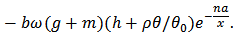 Therefore
Therefore 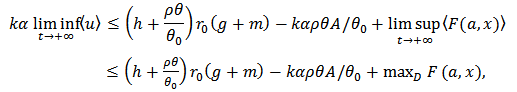
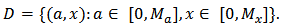 Let
Let 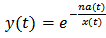 . Define
. Define 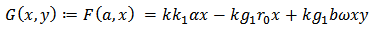
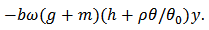 Now we want to know the range of y(t). Using equations (1) and (2),
Now we want to know the range of y(t). Using equations (1) and (2), 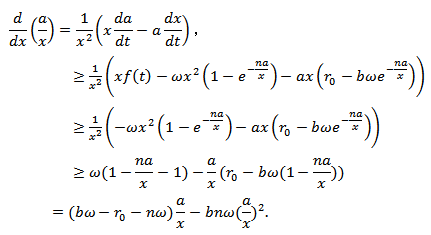 If
If 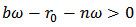 , then the standard comparison theorem results in
, then the standard comparison theorem results in 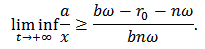 If
If 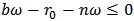 , then at least
, then at least 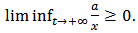 According to the meaning of
According to the meaning of 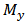 , we have
, we have 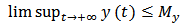 . Thus
. Thus 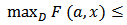
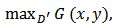 where
where 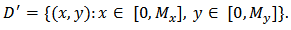 Let
Let 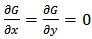 . We get
. We get 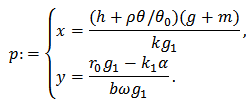 Since
Since 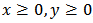 , then
, then 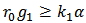 . The value of
. The value of 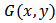 at point p gives
at point p gives 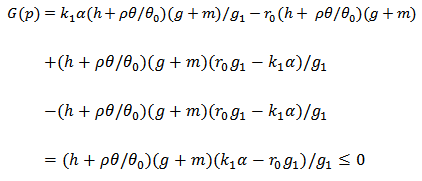 Since
Since 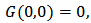 we can assert that
we can assert that 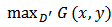 must be taken on the boundary of
must be taken on the boundary of 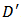 . When
. When 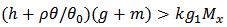 and
and 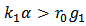 , then
, then 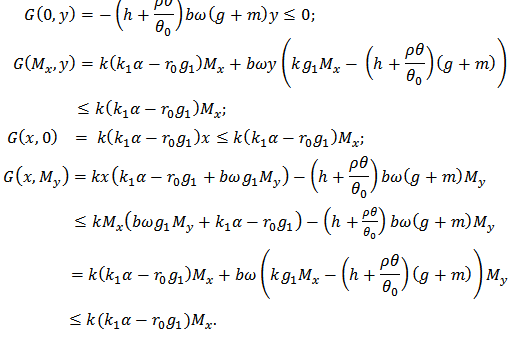 So
So 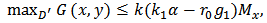 and since
and since 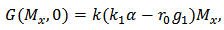 then
then 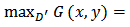
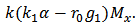 Similarly, when
Similarly, when 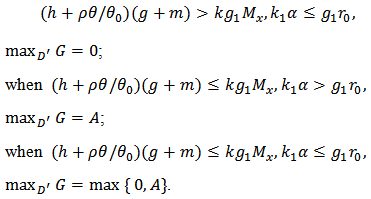 Using inequality (14), it contradicts with the conditions of theorem 2 accordingly.
Using inequality (14), it contradicts with the conditions of theorem 2 accordingly.
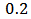 , and the initial values are
, and the initial values are 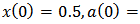
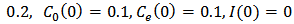 . The following Figure 1 describes the behavior of the population for different exogenous toxicant input rate u in the absence of pollution taxation, Figure 2 shows the behavior of the population in the presence and absence of pollution taxation.
. The following Figure 1 describes the behavior of the population for different exogenous toxicant input rate u in the absence of pollution taxation, Figure 2 shows the behavior of the population in the presence and absence of pollution taxation. 
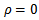

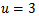

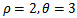

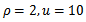
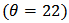 is imposed on the emitters, the balanced amount of the population will return to 5.25 from 1.4 quickly (Figure 4). The taxation coefficient
is imposed on the emitters, the balanced amount of the population will return to 5.25 from 1.4 quickly (Figure 4). The taxation coefficient 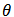 is the key parameter which needs to be chosen very carefully in order to maintain the equilibrium level of population.
is the key parameter which needs to be chosen very carefully in order to maintain the equilibrium level of population.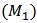 reduces to the system in [9] if there is no pollution taxation. Conditions which guarantee the persistence or extinction of the system are also given. The threshold between persistence and extinction is
reduces to the system in [9] if there is no pollution taxation. Conditions which guarantee the persistence or extinction of the system are also given. The threshold between persistence and extinction is 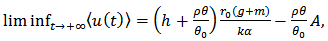 when the conditions of theorem 1 and (I) of theorem 2 are satisfied. In [9] this threshold is
when the conditions of theorem 1 and (I) of theorem 2 are satisfied. In [9] this threshold is 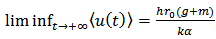 . By numerical simulation, it is shown that the amount of population decreases as the cumulative rate of the emission of the toxicant from external sources increases. So we need to control the emission rate of toxicant from external sources. Moreover, we note that when taxation are imposed on emitters of toxicant, the amount of population increases and shift more near to the level when the ecosystem is in the absence of toxicant.
. By numerical simulation, it is shown that the amount of population decreases as the cumulative rate of the emission of the toxicant from external sources increases. So we need to control the emission rate of toxicant from external sources. Moreover, we note that when taxation are imposed on emitters of toxicant, the amount of population increases and shift more near to the level when the ecosystem is in the absence of toxicant. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML