Kenneth Miebaka Oba, Abiye Abiye Abere
Department of Civil Engineering, Rivers State University, Port Harcourt, Nigeria
Correspondence to: Kenneth Miebaka Oba, Department of Civil Engineering, Rivers State University, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The Transportation problem of shipping sand from four supply locations to three demand locations for Julius Berger construction company in Port Harcourt was solved and optimised by the use of transportation modelling. The study was done for standard 20tons truckload of sand from the various supply locations. Costs of transporting the material were analysed with the North-West Corner, Least Cost, and Vogel’s approximation methods to determine the initial feasible solution. The Vogel’s approximation method turned out to give the best shipping cost. Finally, the Modified Distribution method was used to determine the optimum shipping cost to the tune of $987 or (₦402,696 as at July 2020). A computerised approach, using Microsoft Excel solver was also used to compare the results. The exact results were obtained.
Keywords:
Cost of Sand, Transportation model, Optimization of Shipping Cost
Cite this paper: Kenneth Miebaka Oba, Abiye Abiye Abere, Optimization of Shipping Cost of Sand for Selected Construction Projects of Julius Berger, International Journal of Construction Engineering and Management , Vol. 12 No. 1, 2023, pp. 16-20. doi: 10.5923/j.ijcem.20231201.02.
1. Introduction
This The wide use of sand as fine aggregate for the production of cement concrete, asphalt concrete, masonry, sandcrete, tiling finishes, soil stabilization, sub-base, paving and many more, has continuously reaffirmed the great significance of sand in the construction industry. Most times, sand is mined or dredged, and dumped at a particular site(s) close to its mining location. It is later transported (or shipped) from its initial supply location(s) or dumpsite(s) to various demand locations. This process of moving construction materials from one location to another is also key in the industry. However, studies have shown that transportation of construction materials has been taken a bit lightly during procurement planning and risk assessment [1]. Construction managers have also had challenging experiences shipping materials, especially sand to their various demand sites or locations. This often comes with management of transportation cost, time, personnel, purpose of material, distance to be covered, vehicle to be used, vendors, local authorities and traffic. All these and more will contribute to the overall transportation cost, otherwise known as shipping cost. There is therefore a need to adopt a standard process to optimise (minimize) the transportation or shipping cost.Several studies [2]-[9] have been carried out on the management and transportation of construction materials and other commodities. [9] also carried out a study for the management, planning, control, handling and purchasing of materials. In a bid to further study and improve transportation of items from one location to another, [4] developed a transportation model based on a modified generic algorithm for the vehicle fleet. Several other studies and models [2], [6]-[8] have been carried out in the past, but in all of these, none has addressed the problem of transportation of sand for construction purposes.For this study, Julius Berger, a leading construction company in Nigeria and Africa was taken as a case study. The company in the last seven years has been working on several road construction, bridge construction, and building construction projects for the Rivers state Government in Nigeria. The company has the most number of construction projects awarded to a single company within the period of this research (between years 2015 and 2022) in Rivers State, Nigeria. These projects are located in the city of Port Harcourt, the capital city of Rivers state, and oil and gas hub of Nigeria. The city’s high population, traffic congestion and few amount of roads has made it difficult for transporting materials, especially sand, usually transported in large trucks across the city. This research intends to address the issue of transportation of sand from various locations to various demand locations, cost effectively with reduced number of trips, which will result in reduced amount of methane gas emission from trucks.
2. Materials and Methods
Sharp river sand was used in this research. Interviews were conducted on some project managers, site engineers, site supervisors and dumper truck drivers of Julius Berger Construction Company. The associated costs, and required number of trips per day were collated. Table 1 shows the cost of transporting sand from four dumpsites in Port Harcourt to three project locations in the same city. The amounts are in U.S Dollars, haven converted from Nigerian Naira at ₦408 per US$ as at July 2020, since the data was collected in 2020. The costs include cost of hiring a truck, dredging or buying the sand, fuelling the vehicles, paying the driver, taxes and homages. The total cost was then divided by 20 tons to obtain the values in the table below.Table 1. Transportation Distribution from Supply to Demand locations
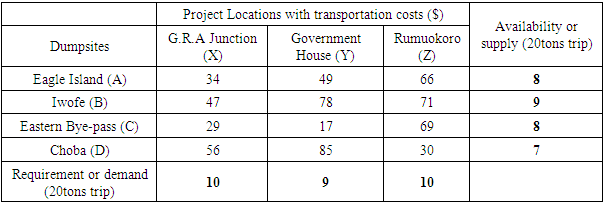 |
| |
|
2.1. The Simplex Approach of Solving Transportation Problem
According to [10], the following are the steps for solving a transportation problem:i. Formulate the problem and arrange the data in matrix formii. Obtain an initial feasible solution by the following three methods (choose the lowest result from these three):• North-West Corner method• Least Cost method (or inspection method)• Vogel’s approximation method (or penalty method, or opportunity cost method)iii. Test the chosen feasible solution for optimality using either of the following two methods:• Modified Distribution (MoDi) method• Stepping stone methodiv. Update the solution and repeat the test until the optimal solution is reached.The general form of a transportation model is: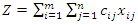 | (1) |
Subject to the constraints:Supply constraint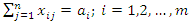 | (2) |
Demand constraint 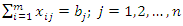 | (3) |
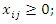 for all i and j
for all i and j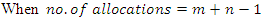 | (4) |
it is a non-degenerate solutionHowever, when 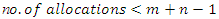
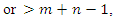 | (5) |
then degenerate.For there to be a feasible solution,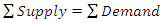 | (6) |
This is called the rim condition.However, if 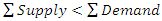 , add a dummy row whose supply (availability) is
, add a dummy row whose supply (availability) is 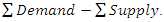 Similarly, if
Similarly, if 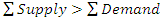 , add a dummy column whose demand (requirement) is
, add a dummy column whose demand (requirement) is 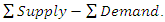 For the given data,m is 4, n is 3, and 4+3-1 is 6.
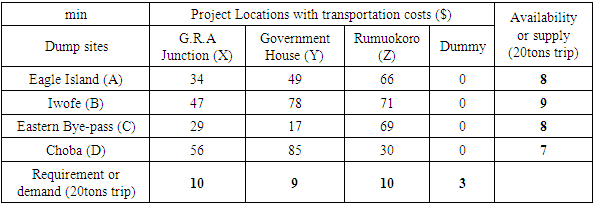
For the given data,m is 4, n is 3, and 4+3-1 is 6.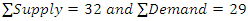 Since supply is greater than demand, there will be a dummy column with a total of 32-29 = 3. This also means that the number of allocation becomes 7.Hence, Table 2 shows the modifications accordingly.
Since supply is greater than demand, there will be a dummy column with a total of 32-29 = 3. This also means that the number of allocation becomes 7.Hence, Table 2 shows the modifications accordingly.Table 2. Modified transportation Distribution from Supply to Demand locations
 |
| |
|
3. Results and Discussions
3.1. The North-West Corner Method
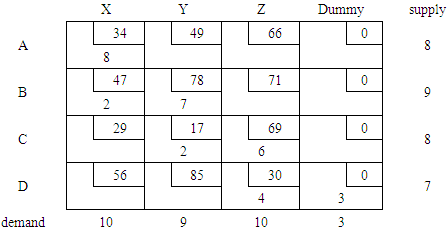
This was used to obtain an initial feasible solution as shown in Table 3 below.Table 3. Initial solution by North-West Corner method
 |
| |
|
The total shipping cost = (8*34) + (2*47) + (7*78) + (2*17) + (6*69) + (4*30) + (3*0) = $1,480
3.2. The Least Cost Method
This was used to obtain an initial feasible solution as shown in Table 4 below.Table 4. Initial solution by Least Cost method
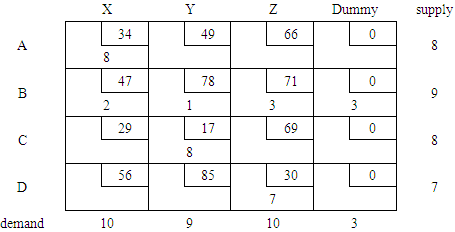 |
| |
|
The total shipping cost = (8*34) + (2*47) + (1*78) + (3*71) + (3*0) + (8*17) + (7*30) = $1,003
3.3. The Vogel’s Approximation Method
This was used to obtain an initial feasible solution as shown in Table 5 below. | Table 5. Initial solution by Vogel’s Approximation method |
The total shipping cost = (7*34) + (1*49) + (3*47) + (3*71) + (3*0) + (8*17) + (7*30) = $987
3.4. The Optimal Solution
This Modified Distribution (MoDi) method was used to obtain an optimal feasible solution as shown in Table 6 below.For occupied cells,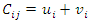 | (7) |
and for unoccupied cells,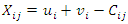 | (8) |
Where Cij is the transportation cost for each cell, u, v, and X are constants. Note that the respective Cij for the occupied and unoccupied cells will be used distinctly in Eqs. (7) and (8). The constant, u1 is always set as zero. The method that gave the best result from the initial feasible solutions was the Vogel’s Approximation method. Hence, the results from Table 6 were used for the development of the optimal solution.Table 6. Determination of constants
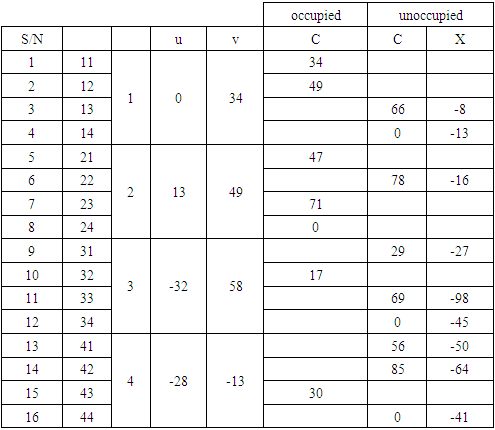 |
| |
|
The X values are all negative, hence the solution is optimal and there is no need for any further iteration.Table 7. Optimized solution using MoDi
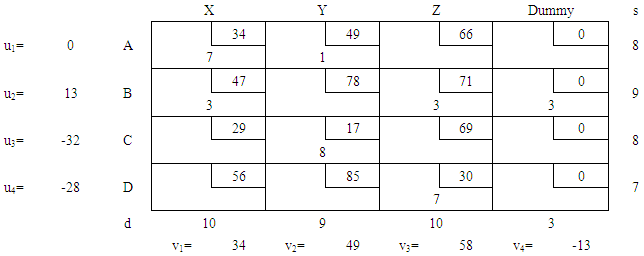 |
| |
|
The optimum shipping cost = (7*34) + (1*49) + (3*47) + (3*71) + (3*0) + (8*17) + (7*30) = $987Alternatively, Microsoft Excel solver can be used to determine the optimum shipping cost as shown in Table 8.Table 8. Optimized solution using MS Excel
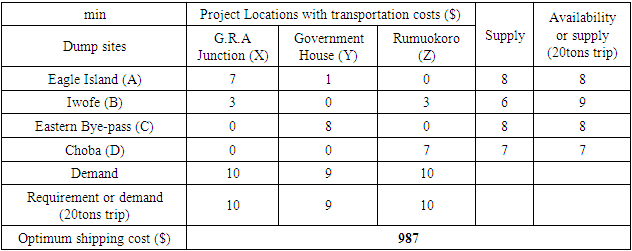 |
| |
|
The optimum shipping cost in Naira is ₦402,696. There were 7 and 6 allocations when the manual and MS excel approaches of transportation modelling were used respectively. However, the same result was obtained.
4. Conclusions
The four supply locations were to transport sand to three construction sites (demand locations). The North-West Corner, Least Cost, and Vogel’s Approximation methods were used for the initial feasible solution, resulting in $1,480.00, $1,003.00, and $987.00 respectively. Vogel’s Approximation method, haven given the best result was further analysed by the use of Modified Distribution method to obtain the optimal solution to the transportation problem. The Transportation modelling application to transportation of sand for construction purposes has been given a more state-of-the-art approach by virtue of this research. Stakeholders and professionals in the construction industry can more accurately and confidently plan, manage, and execute their construction projects by virtue of the contributions from this study.
References
| [1] | A. Ahmadian, A. Akbarnezhad, T. H. Rashidi, and S. T. Waller, “Importance of planning for the transport stage in procurement of construction materials,” in 31st International Symposium on Automation and Robotics in Construction and Mining, ISARC 2014 - Proceedings, 2014, no. Isarc, pp. 466–473. |
| [2] | C. Pilot and S. Pilot, “A model for allocated versus actual costs in assignment and transportation problems,” Eur. J. Oper. Res., vol. 112, no. 3, pp. 570–581, 1999. |
| [3] | P. McCann, “A proof of the relationship between optimal vehicle size, haulage length and the structure of distance-transport costs,” Transp. Res. Part A Policy Pract., vol. 35, no. 8, pp. 671–693, Sep. 2001. |
| [4] | Q. Yan and Q. Zhang, “The Optimization of Transportation Costs in Logistics Enterprises with Time-Window Constraints,” Discret. Dyn. Nat. Soc., vol. 2015, 2015. |
| [5] | F. Zukhruf, R. B. Frazilla, B. Jzolanda Tsavalista, D. Andreas, S. Andhika, and L. Jagad Slogo, “Developing an integrated restoration model of multimodal transportation network,” Transp. Res. Part D Transp. Environ., vol. Under Revi, no. August, p. 103413, 2021. |
| [6] | E. Palkina, “Transformation of business models of logistics and transportation companies in digital economy,” in X International Scientific Siberian Transport Forum, 2022, vol. 63, pp. 2130–2137. |
| [7] | H. Rodriguez-Deniz, M. Villani, and A. Voltes-Dorta, “A multilayered block network model to forecast large dynamic transportation graphs: An application to US air transport,” Transp. Res. Part C, vol. 137, pp. 1–24, 2022. |
| [8] | W. Terazumi, H. Murata, and H. Kobayashi, “System dynamics model for changing transportation demand during the pandemic in Japan,” in 29th CIRP Life Cycle Engineering Conference, 2022, pp. 805–810. |
| [9] | A. Zeb, S. Malik, S. Nauman, H. Hanif, and M. O. S. Amin, “Factors Affecting Material Procurement, Supply and Management in Building Projects of Pakistan: A Contractor’s Perspective,” in Proceedings of 2015 International Conference on Innovations in Civil and Structural Engineering, 2015, pp. 170–175. |
| [10] | J. K. Sharma, Operations Research: Theoty and Applications, 6th ed. New Delhi: Trinity Press, 2016. |



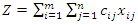
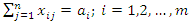
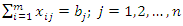
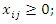 for all i and j
for all i and j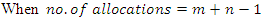
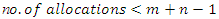
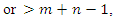
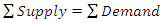
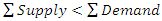 , add a dummy row whose supply (availability) is
, add a dummy row whose supply (availability) is 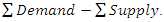 Similarly, if
Similarly, if 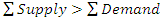 , add a dummy column whose demand (requirement) is
, add a dummy column whose demand (requirement) is 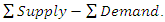 For the given data,m is 4, n is 3, and 4+3-1 is 6.
For the given data,m is 4, n is 3, and 4+3-1 is 6.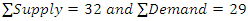 Since supply is greater than demand, there will be a dummy column with a total of 32-29 = 3. This also means that the number of allocation becomes 7.Hence, Table 2 shows the modifications accordingly.
Since supply is greater than demand, there will be a dummy column with a total of 32-29 = 3. This also means that the number of allocation becomes 7.Hence, Table 2 shows the modifications accordingly.
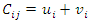
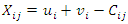
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML





