-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Construction Engineering and Management
p-ISSN: 2326-1080 e-ISSN: 2326-1102
2016; 5(2): 42-54
doi:10.5923/j.ijcem.20160502.02

A Comparative Study for Fuzzy Ranking Methods in Determining Economic Life of Equipment
A. M. El-Kholy1, A. M. Abdelalim2
1Civil Engineering Dept., Faculty of Engineering, Beni-Suef University, Beni-Suef, Egypt
2Civil Engineering Dept., Faculty of Engineering at Mataria, Helwan University, Egypt
Correspondence to: A. M. El-Kholy, Civil Engineering Dept., Faculty of Engineering, Beni-Suef University, Beni-Suef, Egypt.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Replacing the equipment at it's economic life reducing the direct cost of construction projects, which leads to increasing the probability of winning bids. This problem involves capital cost, scrap value, maintenance cost, and rate of interest. The main aim of this paper is to study the effect of fuzzy ranking method based on centroid indices in determining replacement time (economic life) of equipment. Normal trapezoidal fuzzy numbers were used for their simplicity and for the comparison of different ranking methods. The time value of money was considered. Nine ranking methods were considered. Two examples were conducted to demonstrate the effect of fuzzy ranking method on economic life of equipment. The main contribution of this research is that five methods give the same results for the economic life for fuzzy replacement problem which are consistent with human intuition. These methods are: Cheng [1], Chu and Taso [2], Wang et al. [3], Dat et al. [4] and Gani and Mohamed [5]. On the other hand, Chen and Chen [6] and Allahviranloo and Saneifard [7] ranking methods give another replacement time which is also consistent with human intuition. Yager [8] and Chen and Chen [9] ranking methods give different results for replacement time which are not consistent with human intuition.
Keywords: Fuzzy numbers, Fuzzy ranking method, Time value of money, Economic life, Fuzzy replacement problem
Cite this paper: A. M. El-Kholy, A. M. Abdelalim, A Comparative Study for Fuzzy Ranking Methods in Determining Economic Life of Equipment, International Journal of Construction Engineering and Management , Vol. 5 No. 2, 2016, pp. 42-54. doi: 10.5923/j.ijcem.20160502.02.
Article Outline
1. Introduction
- Replacement Problem (RP) is one of the practical areas in economic decision analysis for our real world system. It is used in engineering economics to determine an optimal decision for maintenance and replacement purposes. Park [10] reported that replacement time or economic life of asset is the remaining useful life that results in the minimum annual equivalent cost. However, the minimum annual equivalent cost for equipments is an important issue for reducing direct cost of construction projects, which results in increasing the probability of winning bids.When any production facility is new, it works with full operating efficiency. With passage of time and due to usage, it may become old, some of its components wear out, and the operating efficiency of the facility may gradually decreases. To regain the efficiency, maintenance is to be needed. When first maintenance is attended, its performance is slightly reduced. In the second maintenance, it is more reduced than previous one. Like this the facility deteriorates, and finally the operating efficiency reduces to some desired level of performance. Thus, it is not economical to use the facility for further production, as the maintenance cost will be very high, and the unit production cost also increases. Therefore, the replacement of the facility is due at this stage (Biswas and Pramanik [11]). In our real world system, there are elements of uncertainty in the process or its parameters, which may lack precise definition or precise measurement especially when the system involves human judgment. When developing a model of a system of uncertainty, the decision maker can either ignore the uncertainty or try to deal with uncertainty. When, ignoring the uncertainty, the decision maker obtains the results in a deterministic model of the process with precise values of all parameters. To deal with uncertainty, a decision maker uses specific paradigms such as interval analysis, probability theory, fuzzy set theory, possibility theory, or evidence theory. The choice of paradigm depends on the nature of the uncertainty (Biswas and Pramanik [11]).In their work, Biswas and Pramanik [11] considered a realistic replacing problem where capital cost, scrap value and maintenance cost or running cost of equipment are imprecise in nature and represented by positive triangular fuzzy number (TFNs) or trapezoidal fuzzy numbers (TrFNs). They assumed that the replacement of equipment deteriorates with time and the fuzzy maintenance cost goes on increasing with usage or age. Then, they found out optimum time of replacing the item considering the value of money decreases with fuzzy rate of interest that is known as its discounted factor or depreciation ratio. With this discounted factor, they determined the weighted average fuzzy cost, then found the minimum fuzzy average cost. Finally, Comparison of fuzzy average costs was done by a Yager’s ranking method [8]. In this paper, the authors study a realistic view that capital cost, scrap value, maintenance or running cost of equipment are all of trapezoidal fuzzy numbers (TrFNs). They consider the value of money with time in the replacement of equipment that deteriorates with time. The previous definition of economic life given by Park [10] is adopted for determining the replacement year. The main objective of this paper is to compare different fuzzy ranking methods in determining replacement time (economic life) which seek for the minimum equivalent annual cost. Fuzzy ranking methods have been used to transform the fuzzy numbers to crisp version so that any conventional method can be applied to solve the problem. In the current research, for simplicity and for the comparison of different ranking methods, normal fuzzy numbers are only considered.
2. Literature Review
- Many researchers have developed different RP with different criterion. Several RP models are available in the literature. Bellman [12] and Bellman and Dreyfus [13] developed the replacement problem as a dynamic programming (DP). They formulated a discounted DP version of the economic life of equipment and determined analytically the optimal age to replace the equipment. Alchian [14] considered replacement problem, when operating cost of equipment involves linear function of time. Dreyfus and Law [15] discussed RP with exponentially bounded operating costs. In order to introduce a more realistic view, they studied RP where decision can be made stochastically. Ohnishi [16] studied optimal repair and replacement problem under average cost criterion as a semi Markov decision. Wagner [17] formulated a replacement problem as a network and solved for the shortest path that corresponds to the minimum outlay. Oak ford et al [18] generalized the Wagner’s dynamic programming model that allows for multiple challengers and time varying parameters. Lohmann [19] again generalized Wagner’s dynamic model in stochastic concept. Dimitrakos and Kyriakidis [20] considered a system that deteriorates with age and may experience a failure at any time. They developed an algorithm based on the embedding technique and then generate a sequence of improving control limit policy. Mahdavi and Mahdavi [21] discussed an optimization of age replacement policy using reliability based heuristic model. Zhao et al. [22] formulated three kinds of replacement models combined with additive and independent damages. Nezhad et al [23] discussed one stage two-machine replacement strategy based on the Bayesian inference method. Recently, Zvipore et al. [24] developed a comprehensive dynamic programming – based optimization solution methodology to solve equipment replacement optimization problem on the replacement of convey or belts at a Gold Mining Company in Zimbabwe. Sabu et al. [25] discussed the value and importance of replacement in production atmosphere. They focused on striking a balance between the cost and the competitive environment. Also, they discussed the possibilities of equipment replacement to ensure delivering the normal performance of equipment.The theory of Von Neumann and Morhenstern [26] provides the tools necessary to determine the optimal decision when the probabilities are specified for outcomes. To deal with uncertainty, which is different from probability theory, Zadeh [27] developed the concept of fuzzy set theory. This theory has been developed and applied to numerous areas such as control, decision-making, engineering, medicine, investment and finance. The uses of non-probabilistic uncertainty and especially fuzzy sets have caught much attention in the area of economic analysis (Buckley [28]; Buckley [29]; Choobineh, and Behrens [30]). Ward [31] studied discounted fuzzy cash flow problem. Uncertainty occurs in replacement and maintenance decisions in various ways. To solve the fuzzy replacement problem (FRP), Dong and Shash [32] proposed a method to bypass the problem involving interval and fuzzy arithmetic. Hearnes [33] formulated fuzzy versions of the economic life of an asset model and the finite single asset replacement problem. Chiu and Park [34] used fuzzy numbers in cash flow analysis and provide a good survey of the major methods for ranking mutually exclusive fuzzy projects. Biswas and Pramanik [35] developed a method of finding the optimal replacement time of equipment for fuzzy replacement problem with trapezoidal fuzzy numbers and triangular fuzzy numbers using Yager’s ranking method [8]. They don’t consider time value of money.
3. Research Scope and Methodology
- In the current research, a comparative study for different fuzzy ranking methods in determining economic life of equipment which seek for the minimum equivalent annual cost will be conducted. A standard methodology will be adopted. As an initial step to meet the objectives, previous research papers that deal with the optimal replacement time of equipment for fuzzy replacement problem were reviewed in the previous section. The next step is to describe the normal trapezoidal fuzzy number. Fuzzy ranking methods based on centroid indices are then presented. Methodology adopted for the determination of replacement time for equipment are then explained. The next step is to apply these steps to an example project to show how to determine the economic life for each ranking method. A second example is then highlighted to draw a conclusion. Analysis of the results for the two examples helps indicate the effect of fuzzy ranking method based on centroid indices on economic life for fuzzy replacement problem. Based on the results, conclusions are drawn in the last section.
4. Generalized and Normal Trapezoidal Fuzzy Number
- Kaufmann and Gupta, 1988, cited by kumar et al., [36] reported that a generalized fuzzy number, A (a,b,c,d;w) is said to be a generalized trapezoidal fuzzy number if its membership function is given by:
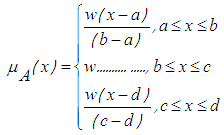 Thorani et al. [37] reported that, it is customary to write a trapezoidal fuzzy number as A (a,b,c,d;w). If w = 1, then A (a,b,c,d;1) is a normalized fuzzy number, otherwise A is said to be a generalized or non-normal fuzzy number.
Thorani et al. [37] reported that, it is customary to write a trapezoidal fuzzy number as A (a,b,c,d;w). If w = 1, then A (a,b,c,d;1) is a normalized fuzzy number, otherwise A is said to be a generalized or non-normal fuzzy number.5. Fuzzy Ranking Methods
- Ranking fuzzy numbers is usually used in decision-making, data analysis, artificial intelligence, economic systems and operation research. In a fuzzy environment, ranking is a very important decision making procedure. In order to rank fuzzy numbers, one fuzzy number needs to be evaluated and compared to the others, but this may not be easy. Since fuzzy numbers are represented by possibility distributions, they can overlap with each other and, thus, it is difficult to determine clearly whether one fuzzy number is larger or smaller than another (Kwang and Lee, [38]). In recent years, many methods have been proposed for ranking different types of fuzzy numbers and can be classified into four major classes; preference relation, fuzzy mean and spread, fuzzy scoring and linguistic expression, but each method appears to have advantages as well as disadvantages (Chen and Hwang, [39]). One of the most commonly used methods under the class of fuzzy scoring is the centroid point method. Therefore, in this paper the centroid point methods in ranking fuzzy numbers are only applied. The famous ranking methods based on centroid point in almost previous researches are applied here: Yager [8], Cheng [1], Chu and Taso [2], Chen and Chen [6], Wang et al. [3], and Chen and Chen [9]. In addition to three new methods, these are: Dat et al. [4], Allahviranloo and Saneifard [7], and Gani and Mohamed [5].Ever since Yager [8] presented the centroid concept in the ranking approach, numerous ranking techniques using the centroid concept have been proposed and investigated. Yager [8] was the first researcher to propose a centroid-index ranking method to calculate the value of fuzzy number A as
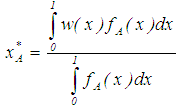 | (1) |
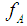 denotes the membership function of the fuzzy number A. When w(x) = x, the value
denotes the membership function of the fuzzy number A. When w(x) = x, the value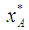 becomes the geometric Center of Gravity (COG) with
becomes the geometric Center of Gravity (COG) with 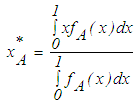 . The larger the value is of
. The larger the value is of 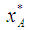 , the better the ranking of A. However, Yager [8] made no assumption on the normality and on the convexity of the fuzzy number. Cheng [1] used a centroid-based distance approach to rank fuzzy numbers. For a trapezoidal fuzzy number A = (a,b,c,d;ϖ ), the distance index can be defined as:
, the better the ranking of A. However, Yager [8] made no assumption on the normality and on the convexity of the fuzzy number. Cheng [1] used a centroid-based distance approach to rank fuzzy numbers. For a trapezoidal fuzzy number A = (a,b,c,d;ϖ ), the distance index can be defined as: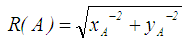 | (2) |
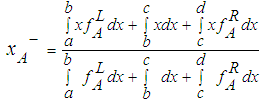 | (3) |
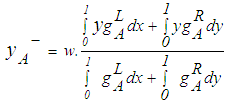 | (4) |
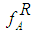 and
and 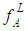 are the respective right and left membership functions of A, and
are the respective right and left membership functions of A, and 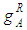 and
and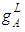 are the inverse of
are the inverse of 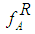 and
and 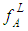 respectively. The larger the value of
respectively. The larger the value of 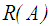 , the better the ranking will be of A. For trapezoidal fuzzy numbers equations 3 and 4 becomes as given in Eq.(s) 5 and 6.
, the better the ranking will be of A. For trapezoidal fuzzy numbers equations 3 and 4 becomes as given in Eq.(s) 5 and 6. 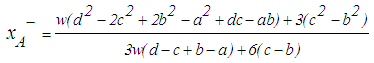 | (5) |
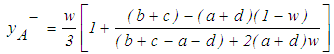 | (6) |
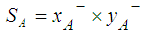 | (7) |
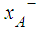 is as defined in Cheng [1] and
is as defined in Cheng [1] and 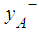 as given in Eq. 8. The larger the value is of
as given in Eq. 8. The larger the value is of 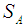 , the better the ranking will be of A.
, the better the ranking will be of A.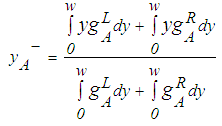 | (8) |
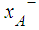 and
and 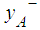 .Dat et al. [4] declared that the drawback of Chu and Tsao [2] ranking method is that if
.Dat et al. [4] declared that the drawback of Chu and Tsao [2] ranking method is that if 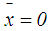 , then the value of
, then the value of 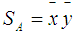 is a constant zero. In other words, the fuzzy numbers with centroids (0,y1) and (0,y2), (y1≠y2) are considered the same. This is unreasonable.Chen and Chen [6] proposed an approach for ranking generalized trapezoidal fuzzy numbers based on centroid point and standard deviations to overcome the drawbacks of Cheng’s [1] and Yager’s [8] approaches. The ranking value for a generalized trapezoidal fuzzy number
is a constant zero. In other words, the fuzzy numbers with centroids (0,y1) and (0,y2), (y1≠y2) are considered the same. This is unreasonable.Chen and Chen [6] proposed an approach for ranking generalized trapezoidal fuzzy numbers based on centroid point and standard deviations to overcome the drawbacks of Cheng’s [1] and Yager’s [8] approaches. The ranking value for a generalized trapezoidal fuzzy number 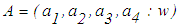 (Rank (A)) is given in Eq. 9. The larger the value of Rank (A), the better the ranking of A.
(Rank (A)) is given in Eq. 9. The larger the value of Rank (A), the better the ranking of A.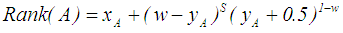 | (9) |
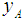 ,
, 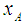 and
and 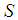 are as given in Eq.(s) 10-12.
are as given in Eq.(s) 10-12. 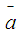 as given in Eq.13.
as given in Eq.13.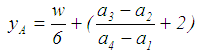 | (10) |
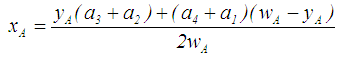 | (11) |
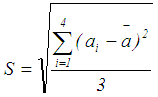 | (12) |
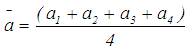 | (13) |
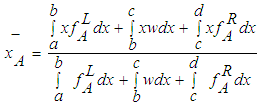 | (14) |
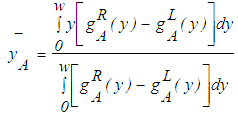 | (15) |
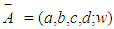 , the value of
, the value of 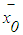 and
and 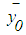 are as given in Eq.(s) 16 and 17.
are as given in Eq.(s) 16 and 17.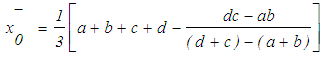 | (16) |
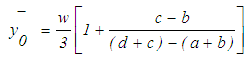 | (17) |
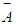 is given in Eq.18. The larger the value of
is given in Eq.18. The larger the value of 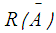 , the better the ranking of A.
, the better the ranking of A.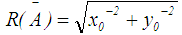 | (18) |
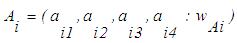 is defined as in
is defined as in 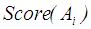 . The larger the value of
. The larger the value of 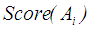 the better the ranking of
the better the ranking of 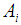 .
.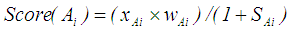 | (19) |
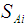 and
and 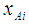 are as given in Eq.(s) 20 and 21, respectively.
are as given in Eq.(s) 20 and 21, respectively.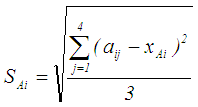 | (20) |
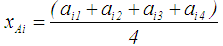 | (21) |
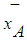 and
and 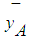 , then the distance between the centroid point,
, then the distance between the centroid point, 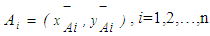 and the minimum point
and the minimum point 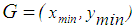 , is proposed as in Eq.22.
, is proposed as in Eq.22. 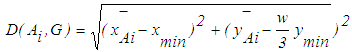 | (22) |
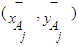 of each fuzzy number Aj , where
of each fuzzy number Aj , where 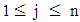 . For trapezoidal fuzzy number Eq.(s) 16 and 17 are equivalent to Eq.(s) 14 and 15, respectively.Step 2: Calculate the maximum crisp value
. For trapezoidal fuzzy number Eq.(s) 16 and 17 are equivalent to Eq.(s) 14 and 15, respectively.Step 2: Calculate the maximum crisp value 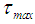 of all fuzzy numbers Aj , where
of all fuzzy numbers Aj , where 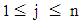 . Step 3: use the point
. Step 3: use the point 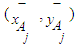 to calculate the ranking value Dist (Aj) of fuzzy numbers Aj , where
to calculate the ranking value Dist (Aj) of fuzzy numbers Aj , where 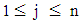 , as in Eq. 23.
, as in Eq. 23.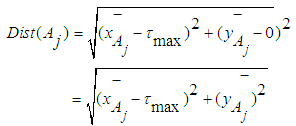 | (23) |
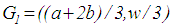 , the centroid of the rectangle is
, the centroid of the rectangle is 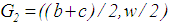 and the centroid of the second triangle is
and the centroid of the second triangle is 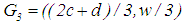 . Thus, they concluded that the centroid
. Thus, they concluded that the centroid 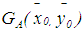 of the triangle with vertices G1, G2, and G3 of the generalized trapezoidal fuzzy number A=(a,b,c,d:w) as
of the triangle with vertices G1, G2, and G3 of the generalized trapezoidal fuzzy number A=(a,b,c,d:w) as 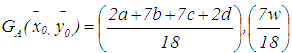 . The ranking function of the generalized trapezoidal fuzzy number A=(a,b,c,d:w) which maps the set of all fuzzy numbers to a set of real numbers is defined as in Eq. 24.
. The ranking function of the generalized trapezoidal fuzzy number A=(a,b,c,d:w) which maps the set of all fuzzy numbers to a set of real numbers is defined as in Eq. 24. 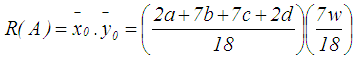 | (24) |
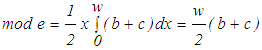 | (25) |
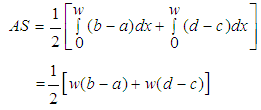 | (26) |
6. Methodology Adopted for the Determination of Replacement Time
- Biswas and Pramanik [35] reported that replacement policy can be classified into the following categories. Case (1): When the equipment deteriorates with time and the value of money does not change with time or changes with time. Case (2): When the units fail completely all of a sudden.In this paper the case when the value of money changes with time is considered. The purpose is to determine the optimum replacement time of equipment whose running or maintenance cost increases with time and the value of money changes during the period considering different fuzzy ranking methods.LetC Capital cost of equipment.S Scrap value of equipment.n number of years that equipment would be in use.Ft maintenance cost for year t. t year number, it may be 1, or 2, or 3,…, or n i rate of interest per year. PV Present Value FV Future value NPV Net Present Value AEA Annual Equivalent Amount Austin et al. [41] reported that the present value PV is given by Eq. 27, whereas Eq. 28 shows annual equivalent amount. Kuhlemeyer et al. [42] gave that, present value (PV) is the current value of a future amount of money, or a series of payments, evaluated at a given interest rate. On the other hand, future value (FV) is the value at some future time of a present amount of money, or a series of payments, evaluated at a given interest rate. In Eq. 27, the factor multiplied by (FV) called single payment present worth factor. He added that, net present value measures the surplus in an investment project at time 0. In other words, net present value (NPV) is the summation of capital cost of equipment, maintenance cost, and subtracting scrap value () of equipment at time 0. On the other hand, annual equivalent amount (AEA) approach is used when companies want to determine whether or not they should replace an existing asset with a new asset (the case here). It can also be used if decided between two new assets [43]. It could be defined as a series of equal payments that are either paid to you or paid from you such as monthly rent payments, car payments [44]. In Eq. 28 the factor multiplied by (PV) called capital recovery factor.
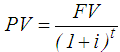 | (27) |
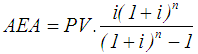 | (28) |
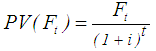 | (29) |
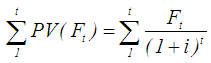 | (30) |
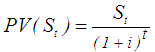 | (31) |
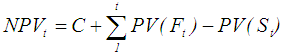 | (32) |
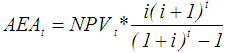 | (33) |
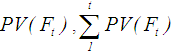 and
and 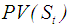 at each year.Step 3: Calculate
at each year.Step 3: Calculate 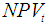 at each year using Eq. 32. Then, determine
at each year using Eq. 32. Then, determine 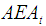 at each year by applying Eq. 33. Replace the equipment at least
at each year by applying Eq. 33. Replace the equipment at least 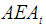 .The following section presents two examples which give a comparison for the effect of fuzzy ranking methods based on centroid indices on economic life of fuzzy replacement problem.
.The following section presents two examples which give a comparison for the effect of fuzzy ranking methods based on centroid indices on economic life of fuzzy replacement problem.7. Application Examples
- In this section two examples are given to show how the methodology adopted step by step for comparing the above methods of ranking for estimating economic life of fuzzy replacement problem. Normal trapezoidal fuzzy numbers are only considered. This is because trapezoidal fuzzy numbers pose several advantages over triangular fuzzy numbers as they are a more generalized form (Bansal, [45]). Also, the Arithmetic behavior of trapezoidal fuzzy numbers is better than triangular fuzzy number and it is more suitable for engineering and scientific problems. On the other hand, normal trapezoidal fuzzy numbers are applied for their simplicity and for the comparison of different ranking methods. Accordingly, normal trapezoidal fuzzy numbers are used in these examples. Analysis of the results for the two examples helps indicate the effect of fuzzy ranking method based on centroid indices on economic life for fuzzy replacement problem.
7.1. First Example
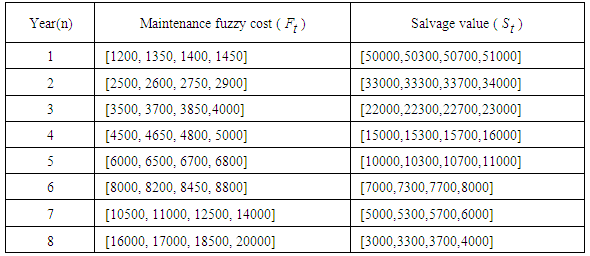
- The data of this example was obtained from Biswas and Pramanik [35]. They did not consider the time value of money, thus they gave one value of salvage value and neglect interest rate. Thus, the authors assumed different values for salvage according to the year. Also, interest rate = 10% per year is assumed.The example data are as follows: a construction company used a certain type of loader whose fuzzy cost (C) in rupees is (61000, 61300, 61700, 62000). Also, they reported that the running cost (maintenance cost (M.C)) in rupees are found from experience (see Table 1, column 2). Assumed different salvage values according to the year are also shown in Table 1, column 3). Solution: (1) To solve this problem, we take RS 1000 =1 unit.Step 1: Choosing ranking method1. For Yager’s [8] ranking method, to get the defuzzyfied value for example for maintenance cost in year 1, F1 = (1.200, 1.350, 1.400, 1.450) the following memberships function and their corresponding indices are as follows:
|
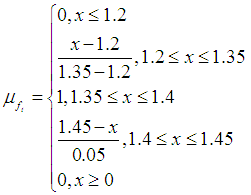 Therefore,
Therefore, 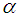 -cut of the fuzzy number (1.200, 1.350, 1.400, 1.450) is
-cut of the fuzzy number (1.200, 1.350, 1.400, 1.450) is 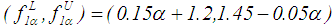 Therefore,
Therefore, 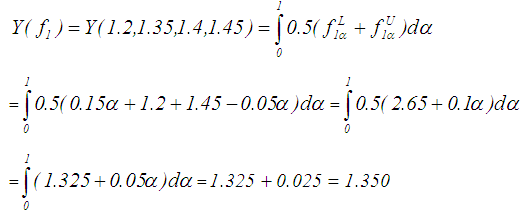 Similarly, the values of
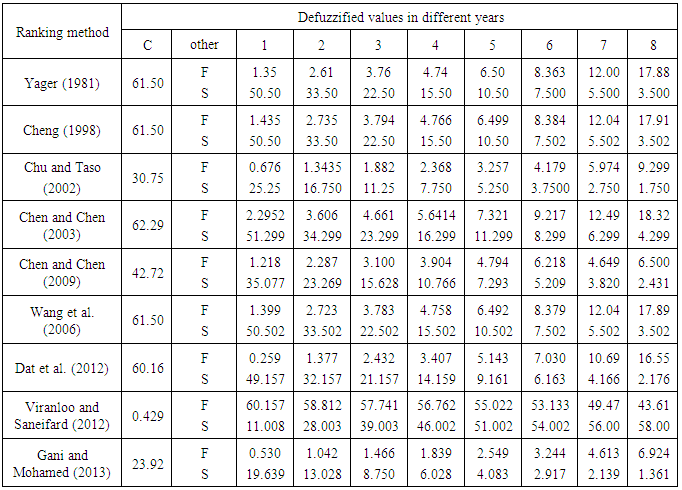
Similarly, the values of  at t = 2, 3, …, 8 are calculated (see Table 2). Also, the defuzzified values of capital cost and salvage value for each year are calculated (see Table 2).
at t = 2, 3, …, 8 are calculated (see Table 2). Also, the defuzzified values of capital cost and salvage value for each year are calculated (see Table 2).
|
 is calculated as follows: apply Eq.5 and 6 to calculate
is calculated as follows: apply Eq.5 and 6 to calculate 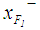 and
and 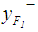 , then determine
, then determine 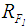 by Eq. 2. See Table 2 for all the defuzzified values.
by Eq. 2. See Table 2 for all the defuzzified values.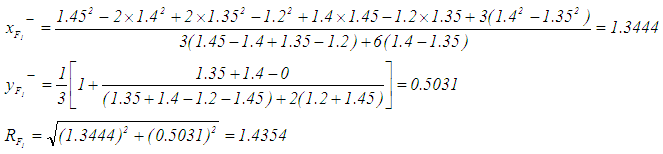 3. For Chu and Taso [2] ranking method,
3. For Chu and Taso [2] ranking method, 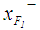 and
and 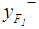 are as given in Cheng (1998), then determine
are as given in Cheng (1998), then determine 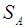 by Eq.7.
by Eq.7.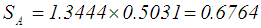 . See Table 2 for the all defuzzified values. 4. For Chen and Chen's [6] ranking method, the defuzzified value for
. See Table 2 for the all defuzzified values. 4. For Chen and Chen's [6] ranking method, the defuzzified value for 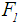 is calculated by applying Eq.(s)10, 13, 12, 11 and 9 to calculate
is calculated by applying Eq.(s)10, 13, 12, 11 and 9 to calculate 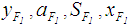 , and
, and 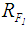 , respectively. See Table 2 for the all defuzzified values.
, respectively. See Table 2 for the all defuzzified values.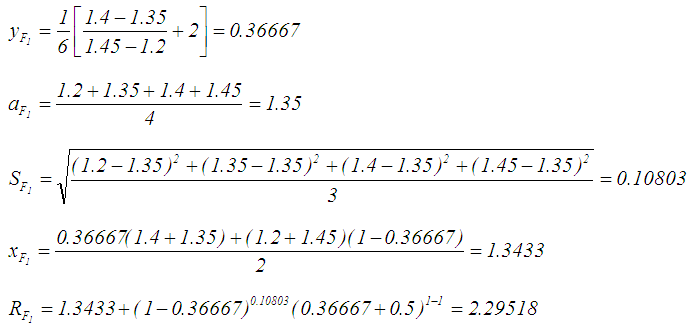 5. For Wang et.al. [3] ranking method, the defuzzified value for
5. For Wang et.al. [3] ranking method, the defuzzified value for 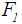 is calculated by applying Eq.(s)16,17 and 18 to calculate
is calculated by applying Eq.(s)16,17 and 18 to calculate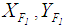 , and
, and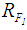 , respectively. See Table 2 for the all defuzzified values.
, respectively. See Table 2 for the all defuzzified values.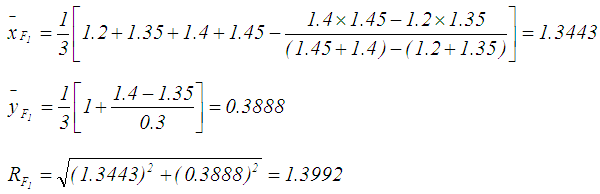 6. For Chen and Chen's [9] ranking method, the defuzzified value for
6. For Chen and Chen's [9] ranking method, the defuzzified value for 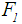 is calculated by applying Eq.13 or 21 to calculate
is calculated by applying Eq.13 or 21 to calculate 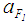 , Eq.12, or 20 to calculate
, Eq.12, or 20 to calculate 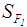 . As previously calculated
. As previously calculated 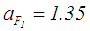 and
and 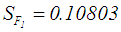 .
. 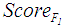 is calculated by using Eq. 19. See Table 2 for the all defuzzified values.
is calculated by using Eq. 19. See Table 2 for the all defuzzified values.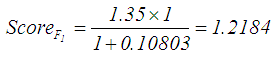 7. For Dat et al. [4] ranking method, the defuzzified value for
7. For Dat et al. [4] ranking method, the defuzzified value for 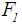 is calculated by applying Eq.(s)16,17 to calculate
is calculated by applying Eq.(s)16,17 to calculate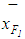 ,
,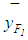 . As given above in Wang et al. (2006)
. As given above in Wang et al. (2006) 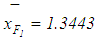 and
and 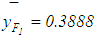 . It must be noted that these values correspond to
. It must be noted that these values correspond to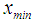 and
and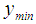 (see Table 1). Thus,
(see Table 1). Thus, 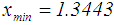 and
and 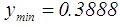 .
. 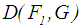 is calculated using Eq. 22. See Table 2 for the all defuzzified values.
is calculated using Eq. 22. See Table 2 for the all defuzzified values.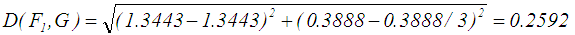 8. For Allahviranloo and Saneifard [7] ranking method, the defuzzified value for
8. For Allahviranloo and Saneifard [7] ranking method, the defuzzified value for 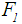 is calculated by applying Eq.(s)16,17 to calculate
is calculated by applying Eq.(s)16,17 to calculate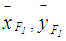 . As given previously
. As given previously 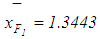 and
and 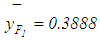 .
. 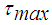 is the maximum
is the maximum 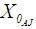 . This value is 60.5 correspond to fuzzy capital cost (61000, 61300, 61700, 62000). Applying Eq. 23,
. This value is 60.5 correspond to fuzzy capital cost (61000, 61300, 61700, 62000). Applying Eq. 23, 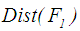 is calculated as given below. See Table 2 for the all defuzzified values.
is calculated as given below. See Table 2 for the all defuzzified values. 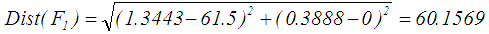 9. For Gani and Mohammed [5] ranking method, the defuzzified value for
9. For Gani and Mohammed [5] ranking method, the defuzzified value for 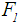 is calculated by applying Eq. 24 to calculate
is calculated by applying Eq. 24 to calculate 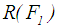 . See Table 2 for all the defuzzified values.
. See Table 2 for all the defuzzified values.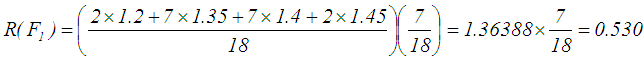 Step 2: Appling Eq.(s) 29, 30, and 31 and using Yager 's [8] ranking method for example gives
Step 2: Appling Eq.(s) 29, 30, and 31 and using Yager 's [8] ranking method for example gives 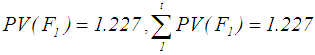 and
and 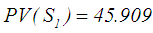 for the first year. Step 3: Apply Eq.(s) 32 and 33 to calculate,
for the first year. Step 3: Apply Eq.(s) 32 and 33 to calculate, 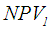 and
and 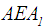 . These values are 16.818 and 18.5, respectively. All other values of
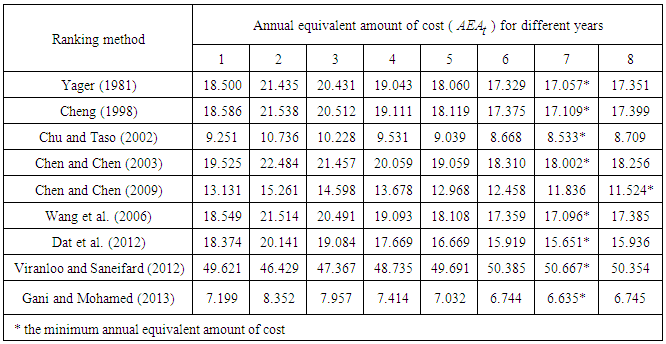
. These values are 16.818 and 18.5, respectively. All other values of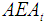 are given in Table 3.
are given in Table 3.
|
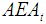 for all ranking methods at different years. From this table it is clear that the minimum annual equivalent amount of cost depends on the ranking method. The year correspond to each minimum value is the year of replacement and this year represents the economic life of equipment. Table 3 shows that eight ranking methods (Yager [8]; Cheng [1];Chu and Taso [2]; Chen and Chen [6]; Wang et al. [3], Dat et al. [4], Allahviranloo and Saneifard [7], and Gani and Mohamed [5] give the same result that the loader should be replaced at the end of 7 th year. According to Chen and Chen [9] ranking method, the loader should be replaced at the end of 8th.
for all ranking methods at different years. From this table it is clear that the minimum annual equivalent amount of cost depends on the ranking method. The year correspond to each minimum value is the year of replacement and this year represents the economic life of equipment. Table 3 shows that eight ranking methods (Yager [8]; Cheng [1];Chu and Taso [2]; Chen and Chen [6]; Wang et al. [3], Dat et al. [4], Allahviranloo and Saneifard [7], and Gani and Mohamed [5] give the same result that the loader should be replaced at the end of 7 th year. According to Chen and Chen [9] ranking method, the loader should be replaced at the end of 8th. 7.2. Second Example
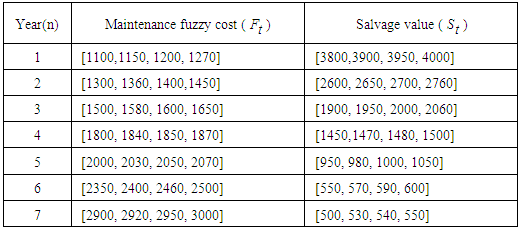
- The data of this example was obtained from Biswas and Pramanik [11]. The fuzzy cost of a machine is US$ (5900, 5950, 6050, 6100). The fuzzy running cost and the salvage value at the end of the year are given in Table 4. The author assumed the interest to be 10% per year. Find when the machine is to be replaced.Solution: To solve this problem, we take $1000 =1 unit. The same steps applied in solving example 1 are applied here. Table 5 shows
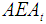 for all ranking methods at different years. From this table it is clear that the minimum annual equivalent amount of cost depends on ranking method. The year corresponds to each minimum value is the year of replacement. Table 5 shows that ranking methods: Cheng [1]; Chu and Taso [2]; Chen and Chen [9]; Wang et al. [3], Dat et al. [4], and Gani and Mohamed [5] give the same result that the loader should be replaced at the end of 6th year. Two ranking methods: Chen and Chen [6] and Allviranloo and Saneifard [7] give that the loader should be replaced at the end of 5 th year. On the other hand, Yager [8] ranking method gives that the loader should be replaced at the end of 7th year.
for all ranking methods at different years. From this table it is clear that the minimum annual equivalent amount of cost depends on ranking method. The year corresponds to each minimum value is the year of replacement. Table 5 shows that ranking methods: Cheng [1]; Chu and Taso [2]; Chen and Chen [9]; Wang et al. [3], Dat et al. [4], and Gani and Mohamed [5] give the same result that the loader should be replaced at the end of 6th year. Two ranking methods: Chen and Chen [6] and Allviranloo and Saneifard [7] give that the loader should be replaced at the end of 5 th year. On the other hand, Yager [8] ranking method gives that the loader should be replaced at the end of 7th year.
|
|
7.3. Analysis of the Results for the Two Examples
- Dat et al. [4] reported that almost no approach can rank fuzzy numbers satisfactorily in all situations. In some situations, almost all methods cannot rank fuzzy numbers correctly with the same centroid point. However, he declared the strong discrimination power of his proposed ranking approach and its advantages through many comparative examples with other ranking methods. Also, he explained that his proposed ranking method is more consistent with human intuitions than existing methods. Taking this issue in consideration together with analysis of the results reveals that: 1. The ranking methods : Cheng [1], Chu and Taso [2], Wang et al. [3], Dat et al. [4] and Gani and Mohamed [5] give the same results for the economic life or replacement time for fuzzy replacement problem which are more consistent with human intuitions. 2. On the other hand, Chen and Chen [6], Allahviranloo and Saneifard [7] ranking methods give the same replacement time which are also consistent with human intuitions. 3. Yager [8] and Chen and Chen [9] ranking methods give different results for replacement time which are not consistent with human intuitions, since economic life always less than normal life.
8. Summary and Conclusions
- In this paper, the fuzzy replacement problem is considered in the sense that the capital cost, scrap value, maintenance or running cost are all imprecise in nature represented by fuzzy numbers. It is more realistic and closer to our daily life situation. In modeling of replacement problem it is often observed that the parameters of the problem are not known precisely. This impreciseness is handled by using fuzzy numbers, as it is expected to express the situation more realistically. In this paper, to deal with this uncertainty, fuzzy replacement problem was presented when the capital cost, scrap value, maintenance or running cost are normal trapezoidal fuzzy numbers. Nine ranking methods have been compared in determining the replacement time (economic life) of equipment. Two numerical examples have been provided to show the effect of ranking method on fuzzy replacement problem. The results revealed that of the nine ranking methods dealt with, five methods give the same results for the economic life or replacement time for fuzzy replacement problem which are consistent with human intuitions. These methods are: Cheng [1], Chu and Taso [2], Wang et al. [3], Dat et al. [4] and Gani and Mohamed [5]. On the other hand, Chen and Chen [6] and Allahviranloo and Saneifard [7] ranking methods give the same replacement time which is also consistent with human intuitions. Yager [8] and Chen and Chen [9] ranking methods give different results for replacement time which are not consistent with human intuitions, since economic life always less than normal life. Replacing the equipment at it's economic life leads to reducing direct cost of construction projects, which intern leads to increasing the probability of winning bids. One limitation of the current research is that the results are true for normal trapezoidal fuzzy numbers.In the future research, the authors hope that the steps adopted for the determination of replacement time of equipment in the current research are applied for non normal fuzzy numbers, i.e. for different values of membership function. On the other hand, further research is required to use the defuzzification method (ranking method) for the annual equivalent amount instead applying defuzzification method firstly for maintenance cost, capital cost and scarp value.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML