| [1] | Ade, A. A. A, Aftab H. M., Ismail, A. R. and Ahmad T. K (2012): Controlling Cost overrun Factors in Construction Projects in Malaysia. Research Journal of Applied Science, Engineering and Technology 5(8): 2621 – 2629. |
| [2] | Anyanwu C. I. (2013): Project Cost Control in the Nigerian Construction Industry; International Journal of Engineering Science Invention www.ijesi.org\\volume2Issue12\\December.2013\\PP.65-71 |
| [3] | Arcila, S. G. (2003): Cost Overruns in Major Construction Projects in the UK. The University of Warwick. |
| [4] | Ashworth, A. and Skitmore, R. M. (1982): Accuracy in Estimating. Occasional Paper No. 27 the Chartered Institute of Building. |
| [5] | Baccarinibi, D., (1987): The Maturing Concept of Estimating Project cost Contingency – A Review. |
| [6] | Patel, M. B. (2004): Project Management Strategic Financial Planning, Evaluation and Control, 2nd Edition, Vikas publishing India. |
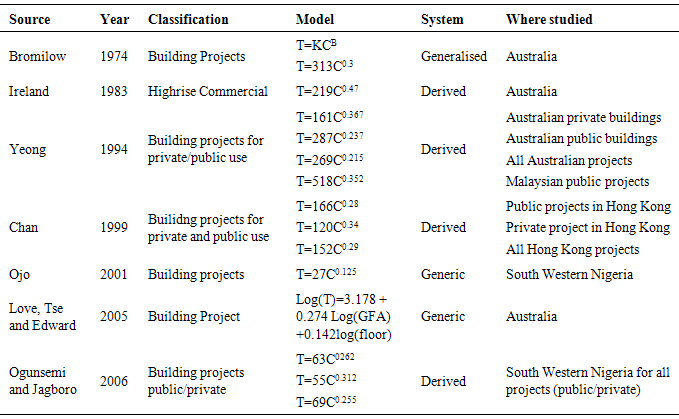
| [7] | Bromilow, F. J. (1974): Measurement and Scheduling of Construction Time and Cost Perforamnce in the Building Industry. The Chartered Builder, 10(9), 57 |
| [8] | Brook, M. (2008) Estimating and Tendering for Construction Work, 3rd ed. Butterworth – Heinemann publishing, Oxford. |
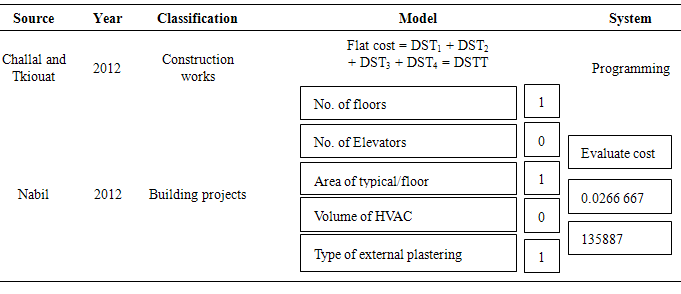
| [9] | Challal, A., and Tkiouat M. (2012): The Design of Cost Estimating Model of Construction Project: Application and Simulation |
| [10] | Chan, A.P.C. (1999): Modelling Building Durations in Hong Kong. Construction Management and Economics, 17(2), 189 – 96. |
| [11] | Cheng M., Tsai H., Sudjono E., (2010): Conceptual Cost Estimates using Evolutionary Fuzzy Hybrid neural Network for Projects in construction Industry. Expert Systems with Applications, Vol. 37, pp. 4224 – 4231. |
| [12] | Clark E. and Doh T. (2011): A Bayesian Evaluation of Alternative Models of Trend Inflation. Economic Research Department. Proceedings of Federal Reserve Bank of Cleveland. |
| [13] | Elhag, T. and Boussabaine, M. (1998): An Artificial Neural System for Cost Estimation of Construction Projects, ARCOM 14th Annual Conference. Reading, UK. |
| [14] | Enshassi, A., Mohamed, S. and Abushaban, S. (2009): Factors Affecting the Performance of Construction Projects in the Gaza Strip. Journal of Civil Engineering and Management 15(3). |
| [15] | FAD Corporate Document Repository. Cost Control in Forest Harvesting and Road Construction. Retrieved from www.fao.org/doc.rep/to579e/to579e03.htm |
| [16] | Failing R. G, Jerry L. J. and Larry D. B. Blevins, (1988): Improving Productivity Through Work Measurement. A Cooperative Approach, American Institute of Certified Public Accountants, New York. |
| [17] | Fox J. (2004): Applied Regression Analysis and Generalized Linear Models. SAGE publishing Inc. |
| [18] | Frimpong, Y., Oluwoye, J. and Crawford, L. (2003): Causes of Delay and Cost Overruns in Construction of Groundwater Projects in a Developing Countries; Ghana as a case study. International Journal of Project Management 21(5). |
| [19] | Cogley T. and Sargent T. J. (2005): Drifts and Volatilities: Monetary Policies and Outcomes in the Post-World War II U.S., Review of Economic Dynamics 8, 262 – 302. |
| [20] | Geweke, J. and Amisano G. (2010): Comparing and Evaluating Bayesian Predictive Distributions of Asset Returns: International Journal of Forecasting, forthcoming. |
| [21] | Geweke, J. and Whiteman C (2006): Bayesian Forecasting: Handbook of Economic Forecasting, G. Elliott, C. Granger, and A Timmermann (Eds.) North Holland: Amsterdam. |
| [22] | Gkritza K., and Labi S. (2008): Estimating Cost Discrepancies in Highway Contracts: Multistep Econometric Approach; Journal of Construction Engineering and Management, Vol. 134 No. 12, pp. 953 – 962. |
| [23] | Gunaydin, M. and Dogan, Z. (2004): A neural Network Approach for early Cost Estimation of Structural Systems of Buildings. International Journal of Project Management, Vol. 22 pp. 595 – 602. |
| [24] | Gupta, S. C. (2004): Fundamentals of Statistics, 6th ed. Himalaya publishing, house India. |
| [25] | Hakan, Y., Tas, E., (2007): A Building Cost Estimation Model based on functional elements. Istanbul turkey |
| [26] | Harris, F., & McCaffer, R. (2005): Modern Construction Management, 5th Edition: EFP Books Services. |
| [27] | Ibrionke (2004): Effective Material Management in a Project Site; The Nigerian Institute of Builders, Vol. 11, page 15. |
| [28] | Ireland, V. (1983): The Role of Managerial Actions in the Cost, Time and quality Performance of High Rise Commercial Building Projects, Unpublished PhD thesis, University of Sydney, Australia. |
| [29] | Jagboro G. O. and Albinu A. A. (2012): The Effects of Construction Delays on Project Delivery in Nigerian Construction Industry: International Journal of Project Management, Vol. 20, No. 8,2002, pp. 593 – 599. |
| [30] | Jergeas, G. F. and Ruwanpura, J. (2010): Why Cost and Schedule Overruns on Mega Oil Sands Projects? Practice Periodical on Structural Design and Construction 15(1). |
| [31] | King R. G. and Watson M. W. (2012) Inflation and Unit Labour Cost: Gerzensee 25th Conference, retrieved at http://www.princeton.edu/mwatson. |
| [32] | Koushki, P. A., Al-Rashid, K. and Kartam, N. (2005): Delays and Cost Increases in the Construction of Private Residential Projects in Kuwait. Construction Management and Economics 23(6). |
| [33] | Kumaraswamy, M. M. and Chan, D. W. M. (1995): Determinants of Construction Duration. Construction Management and Economics, 13(3), 209 – 17. |
| [34] | Laryea, S., & Mensah, S. (2010): The Evolution of Contractors in Ghana. West Africa Bult Environment Research Conference (WABER,) (pp. 88 – 93). Held on 27 – 28 July, 2010 in Pais. |
| [35] | Le-Hoai, L., Lee, Y. and Lee, J. (2008): Delay and Cost Overruns in Vietnam Large Construction Projects. A comparison with other selected countries. KSCE Journal of Civil Engineering 12(6) |
| [36] | Love, P. E. d., Tse, R. Y. C. and Edwards, D. J. (2005): Time-cost Relationships in Australian Building Construction Projects. Journal of Construction Engineering and Management, ASCE, 131(2) 1 – 8. |
| [37] | Milne, J. A. (2003): Tendering and Estimating Procedures; George Godwin Ltd, Publishing. |
| [38] | Morley, J. and Piger J. (2010): The Asymmetric Business Cycle: Review of Economics and Statistics, forthcoming. |
| [39] | Nabil I. E. (2012): Modeling the Parametric Construction Project Cost Estimate using Fuzzy Logic. International Journal of Emerging Technology and Advanced Engineering Vol. 2. |
| [40] | Nida Azhar, N., Farooqui, R., Ahmed, S., (2008): Cost Overrun Factors in Construction Industry of Pakistan. Furst International Conference on Construction in Developing Countries (ICCIDC – 1), “Advancing and Integrating Construction Education, Research & Practice”, 4 – 5, Karachi, Pakistan. |
| [41] | Niebel, Benjamin W., (1993): Motion and Time Study, Erwin |
| [42] | Obiegbu M. E. (2004): Documentation, Monitoring and Cost Analysis of Projects; Being a paper Presented at 29th Annual Conference/General Meetings of the Nigerian Institute of Builders on Effective Management of Capital Projects in Nigeria. |
| [43] | Oforeh E. C. and Alufohai A. J. (2006): Management Estimating and Budgeting for Electrical Installation. Cosine Nig. Ltd. |
| [44] | Ogunsemi D. R. and Jagboro G. O. (2006): Time-cost Model for Building Projects in Nigeria. Construction Management and Economics, No. 24, pp. 253 – 258. |
| [45] | Ojo G. K. (2001): A Study of the Relationship Between Contract Period and Tender Sum of Construction Projects in South – west Nigeria, unpublished MSc thesis, Obafemi Awolowo University, Ile-Ife. |
| [46] | Olawale, Y. A. (2010): Cost and Time Control Practice of Construction Projects in the UK: The Pursuit of effective management control. University of the West of England. |
| [47] | Omoregie, A. and D. Radford, (2006): Infrastructure Delays and Cost Escalation: Causes and effects in Nigeria. Proceeding of 6th International Postgraduate Research Conference, Delft University of Technology and TNO, Netherlands. |
| [48] | Onwusonye, S. I. (2002): Tendering, Estimating and Contractual Arrangement in Building Projects: Practice and Principle. Owerri: Intercontinental Educational Books and Publishers. |
| [49] | Picard, H. E. Industrial Construction Efficiency and Productivity. Transactions, 44th Annual Meeting of AACE International, June 2000, Calgary, AB, Canada. |
| [50] | Picard, H. E., Construction Performance Benchmarking Measurement. Transactions, 46th Annual Meeting of AACE International, June 2002a, Portland, OR |
| [51] | Picard, H. E., Construction Process Measurement and Improvement. Proceedings, 10th Annual Conference on Lean Construction, Aug. 2002b, Gramado, Brazil. |
| [52] | Popescu, C. M., Phaobunjong, K., & Ovararin, N. (2003). Estimating Building Costs. New York: Marcel Dekker, Inc. |
| [53] | Ricketts, J. T. (2000): Systems Fundamentals. In F. S. Merrits, & J. T. Ricketts, Building Design and Construction Handbook, 6th edition (pp. 1.1 – 1.41). New York: McGraw-Hill. |
| [54] | Salami, T. O. (2013): Estimating and Price Analysis in Environmental Science and Engineering, 1st ed. Olad publishing, Ilorin. |
| [55] | Shankar M. E., (2004): Industrial Engineering and Management, Galgota publishing, New-Delhi. |
| [56] | Smets, F. and Wouters R. (2007): Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach, American Economic Review, 97(3): 586 – 606. |
| [57] | Society of American Value Engineers (SAVE/2007): Value Standard and Body of Knowledge, SAVE International Value Standard, 2007 ed. |
| [58] | The Chartered Institute of Buildings Technical Information Papers. |
| [59] | Paper No. 114 Emsley, M. W. and Harris, F. C. (1990): Methods and rates for structural steel erection. |
| [60] | Paper No. 128 Price, A. D. F. (1991): Measurement of construction productivity: Concrete Gangs. |
| [61] | Paper No. 33, Harrison, R. S. (1994): Operational Estimating |
| [62] | Paper No. 64 Ashworth, A. (1986): Cost Models – their history, Development and Appraisal. |
| [63] | Paper No. 65 Ashworth, A. and Elliott, D. A. (1986): Price Books and Schedules of rates |
| [64] | Villani, M. (2009): Steady – State Priors for Vector Auto regressions: Journal of Applied Econometrics 24, 630 – 650. |
| [65] | Vrat, P. (2002): Productivity Management. A systems approach. New-Delhi: Narosa Publishing House. |
| [66] | Yeong, C. M. (1994): Time and Cost Performance of Building Contracts in Australia and Malaysia, unpublished MSc thesis, University of South Australia. |
| [67] | Zadeh, L. A. (1994): Fuzzy Logic: Neural Networks and Soft Computing. Communications of ACM, Vol. 37, No. 3, pp. 77 – 84. |
| [68] | Zadeh, L. A., (2965): Fuzzy Set, Information and Control, Vol. 8, pp. 338 – 353. |

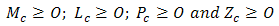 Summarily, recent cost models are somewhat attempts to make cost estimation a predictable quadrature occasioned by their stochastic characteristics as evident in the works of Challal and Tkiouat (2012), Nabil (2012) and Inuwa. et al. (2013).
Summarily, recent cost models are somewhat attempts to make cost estimation a predictable quadrature occasioned by their stochastic characteristics as evident in the works of Challal and Tkiouat (2012), Nabil (2012) and Inuwa. et al. (2013).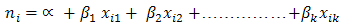
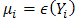 , to the Linear predictor;
, to the Linear predictor;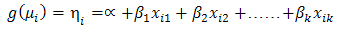
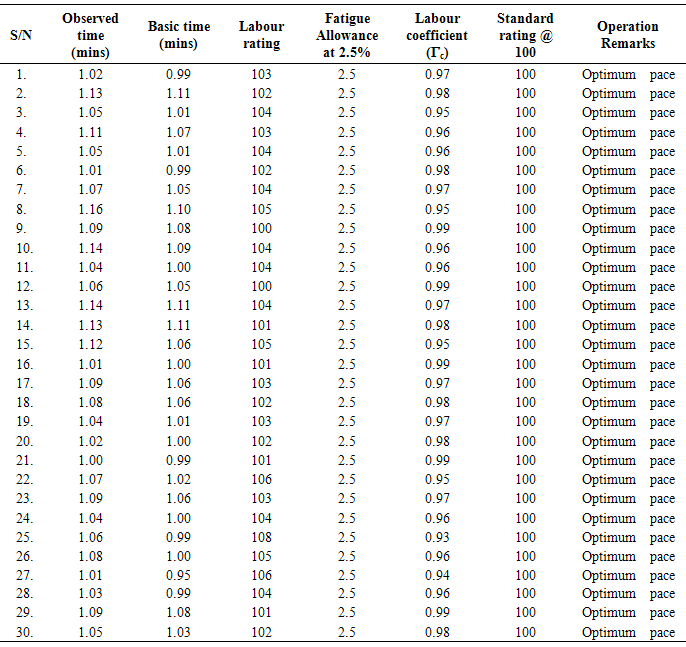
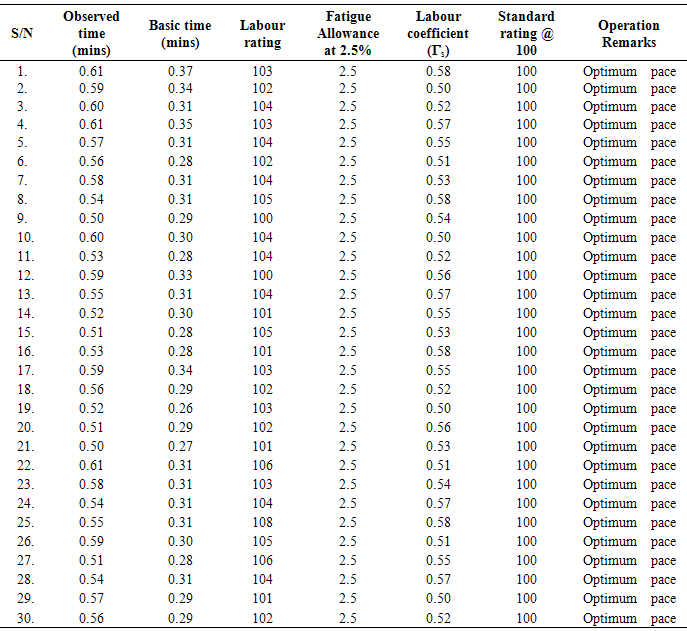
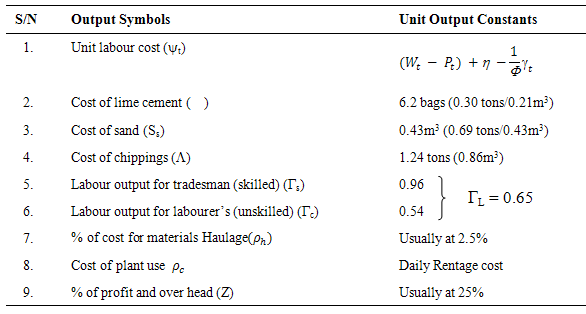
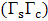 . Productivity study by time and motion study on labour measurement from building and Civil Engineering sites was employed to generate labour output data using the short cycle and time study continuation forms. One hundred and five (105) gang operations were investigated involving mixing, placing and compaction of concrete. This was averaged to observed time for each gang with five (5) operation times. In view of the obvious conditions under which the data were obtained from the 105 gangs, a precise and optimized sample size for analysis was obtained from the distribution using Markov Chain Monte Carlo (MCMC) sampling procedure to 30. This process has been found useful in the works of Clark and Doh (2011), Cogley and Sargent (2005) and assessment check detailed in Villani (2009). The basic time was extrapolated from the theoretical relationship of their ratings below;
. Productivity study by time and motion study on labour measurement from building and Civil Engineering sites was employed to generate labour output data using the short cycle and time study continuation forms. One hundred and five (105) gang operations were investigated involving mixing, placing and compaction of concrete. This was averaged to observed time for each gang with five (5) operation times. In view of the obvious conditions under which the data were obtained from the 105 gangs, a precise and optimized sample size for analysis was obtained from the distribution using Markov Chain Monte Carlo (MCMC) sampling procedure to 30. This process has been found useful in the works of Clark and Doh (2011), Cogley and Sargent (2005) and assessment check detailed in Villani (2009). The basic time was extrapolated from the theoretical relationship of their ratings below;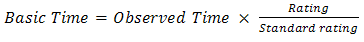
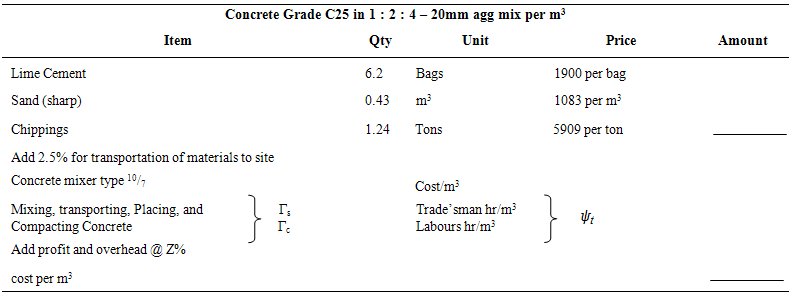
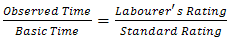
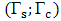 for the gang operations, see Shankar (2004), Vrat (2002) and Milne (2008). The study tabulated for observed time, basic time, labour rating and labour coefficient per gang. The generalized labour coefficient was obtained by Harmonic Mean from;
for the gang operations, see Shankar (2004), Vrat (2002) and Milne (2008). The study tabulated for observed time, basic time, labour rating and labour coefficient per gang. The generalized labour coefficient was obtained by Harmonic Mean from; 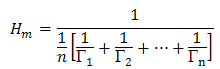 and a comibined mean for
and a comibined mean for 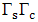 as
as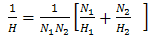
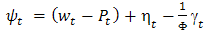
 gave 0.96, while the labourer (unskilled helper) coefficient
gave 0.96, while the labourer (unskilled helper) coefficient  gave 0.54, while the combined mean gave 0.65 on the basis of equation (8).
gave 0.54, while the combined mean gave 0.65 on the basis of equation (8).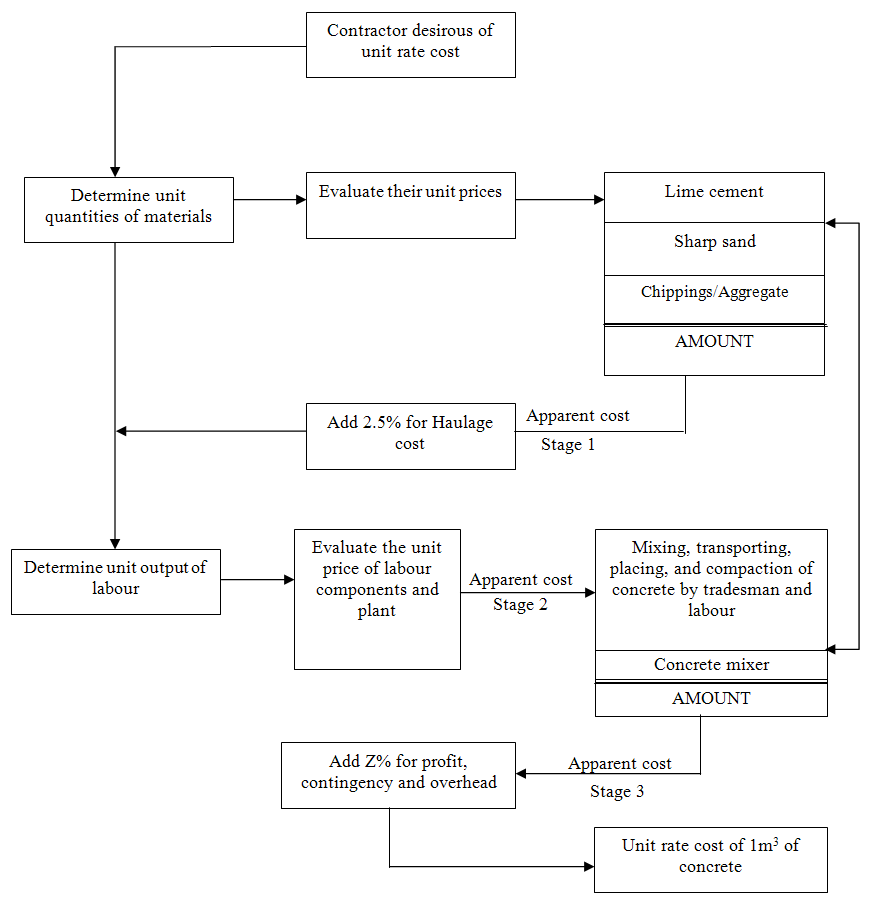
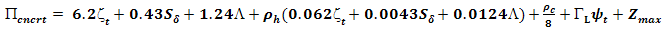
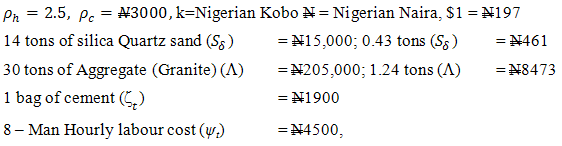 Labour output constant for 1m3 (ΓL) = 0.65∏cncrt. =
Labour output constant for 1m3 (ΓL) = 0.65∏cncrt. = 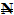 11,780 + 198.23 + 10507 + 2.5(117.8 + 1.9823 + 105.07) + 375 + 2925∏cncrt. = N26,374.38 + Z@ 25% = N32,934.22k per m3
11,780 + 198.23 + 10507 + 2.5(117.8 + 1.9823 + 105.07) + 375 + 2925∏cncrt. = N26,374.38 + Z@ 25% = N32,934.22k per m3 and Z application in the model with respect to end user’s organization’s policy. This model can be used to adjudicate contractors bid on concrete rate with time advantage and less subjective and generalized when the current cost are weighted in respective currencies.
and Z application in the model with respect to end user’s organization’s policy. This model can be used to adjudicate contractors bid on concrete rate with time advantage and less subjective and generalized when the current cost are weighted in respective currencies. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML