Chukwuneke J. L., Achebe C. H., Omenyi S. N.
Department of Mechanical Engineering, Nnamdi Azikiwe University, Awka, Nigeria
Correspondence to: Chukwuneke J. L., Department of Mechanical Engineering, Nnamdi Azikiwe University, Awka, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The energetics of mycobacterium tuberculosis – human sputum interaction mechanisms have been studied. This involved the use of the Hamaker coefficient approach as a surface thermodynamics tool in determining the interaction processes. The surface interfacial energy is explained using van der Waals concept of particle interactions on separation of particulates suspended in a liquid. The methodology employed involved taking sputum samples from twenty infected persons and from twenty uninfected persons for absorbance measurement using a digital Ultraviolet visible Spectrophotometer. The variables required for the computations with the Lifshitz formula were derived from the absorbance data. Matlab software tools were used in the mathematical analysis of the data produced from the absorbance values. The Hamaker constants A11, A22, A33 and the combined Hamaker coefficients A132 and A131 were obtained using the values of the dielectric constant together with the Lifshitz equation. The free energies of adhesion calculated were found to be negative with combined Hamaker coefficient positive. The values of A132abs = 0.21631x10-21Joule (for M-TB infected sputum) and A132abs = 0.18825x10-21joule (for M-TB/HIV infected sputum) were obtained. The implication of this result is the positive value of the absolute combined Hamaker coefficient which entails net positive van der Waals forces demonstrating an attraction between M-TB and the macrophage. This however, implies that infection is very likely to occur. The desired outcome is that the bacteria do not adhere to the macrophage to avoid bacteria penetrating it, in which case a condition for rendering free energy of adhesion positive and combined Hamaker coefficient negative is required.
Keywords:
Absorbance, Dielectric Constant, Energetics, Hamaker Coefficient, Lifshitz Formula, Macrophage, Mycobacterium Tuberculosis, Surface Free Energy, van der Waals Forces
Cite this paper: Chukwuneke J. L., Achebe C. H., Omenyi S. N., Mycobacterium Tuberculosis (M-TB) - Human Sputum Interaction Mechanisms Energetics, International Journal of Biological Engineering, Vol. 5 No. 2, 2015, pp. 23-30. doi: 10.5923/j.ijbe.20150502.01.
1. Introduction
Tuberculosis (TB), a bacterial infection commonly expressed in the respiratory tract, is the leading infectious killer worldwide; it is estimated that one-third of the world’s population is currently infected with TB, and it results in 3 million deaths every year [1]. Human Immunodeficiency Virus (HIV) is a strong risk factor for developing active TB, and TB is the leading cause of death among HIV-positive individuals. Of 4.1 million AIDS deaths in 2004, 13% can be attributed to TB [1].Human Immunodeficiency Virus is one of the leading global health problem caused by an infectious agent. According to a recent World Health Organization (WHO) report there were approximately 34 million people living with HIV in 2010 [2]. There were also 2.7 million new cases and 1.8 million AIDS deaths in 2010. WHO reported that HIV patients experience increasing immunodeficiency due to loss of CD4+ T helper cells and are prone to opportunistic infections by a range of pathogens. The majority of complications are caused by co-infections with mycobacterial. WHO estimated that more than 10 million HIV infected people are co-infected with M-TB, the causative agent of tuberculosis. Mycobacterium TB is among the world’s most deadly infectious diseases despite the long-standing availability of some effective treatment. The steady emergence of multi-drug resistant (MDR), extremely drug-resistant (XDR) and totally drug-resistant strains (TDR) forms of TB is a cause of concern. Globally MDR-TB accounts for roughly 3.6% of all TB cases, but accounts for up to 28% of TB cases in some regions [3-4]. The emergence of MDR, XDR and TDR TB is very worrying due to the increasing difficulty of treating these forms of TB and rendering even the frontline drugs inactive. Infection occurs when a person inhales droplet nuclei containing tubercle bacilli that reach the alveoli of the lungs. These tubercle bacilli are ingested by alveolar macrophages; the majority of these bacilli are destroyed or inhibited. A small number may multiply intracellular and are released when the macrophages die. If alive, these bacilli may spread by way of lymphatic channels or through the blood stream to more distant tissues or organs (including area of the body in which TB disease is most likely to develop: regional lymph nodes, apex of the lung, kidneys, brain, and bone). This process of dissemination primes the immune system for a systemic response.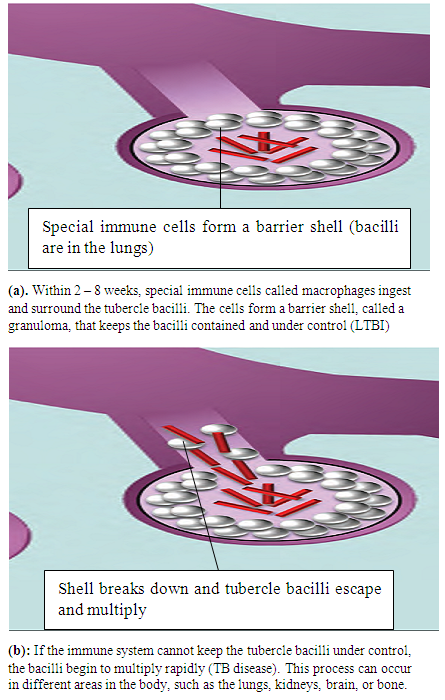 | Figure 1. Pathogenesis of LTBI and TB Disease [4] |
In addition, drugs such as Rifampicin have high levels of adverse effects making them prone to patient incompliance. Another important problems with most of the anti-mycobacterials is their inability to act upon latent forms of the bacillus. To compound the problem further, the complex (vicious) interactions between the HIV and TB makes the treatment of co-infected patients even more challenging [4, 5]. It is against this backdrop that this study explores a novel and rare approach using interfacial free energy approach to seek a way forward in the research on the topic of mycobacterium tuberculosis human system interaction.
2. Theoretical Considerations
2.1. Concept of Interfacial Free Energy
The work done by a force F to move a flat plate along another surface by a distance dx is given, for a reversible process, by;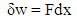 | (1) |
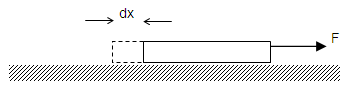 | Figure 2. Schematic Diagram Showing Application of a Force on a Surface [6] |
However, the force F is given by; F = LγWhere; L is the width of the plate and γ is the surface free energy per unit surface area (interfacial free energy). Hence; δw = Lγdx, but; dA =LdxTherefore;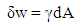 | (2) |
This is the work required to form a new surface of area dA. For pure materials, γ is a function of temperature (T) only, and the surface is considered a thermodynamic system for which the coordinates are γ, A and T. The unit of γ is J/m2. In many processes that involve surface area changes, the concept of interfacial free energy is applicable.
2.2. Thermodynamic Approach to Particle-Particle Interaction
The thermodynamic free energy of adhesion of a particle P on a solid S in a liquid L at a separation d0 [7, 8], is given 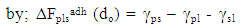 | (3) |
Where ΔFadh is the free energy of adhesion, integrated from infinity to the equilibrium separation distance do; γps is the interfacial free energy between P and S; γpl is that between P and L and γsl that between S and L. For the interaction between the individual components, similar equations can be written also; 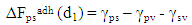 | (4) |
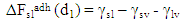 | (5) |
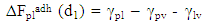 | (6) |
For a liquid, the force of cohesion, which is the interaction with itself is described by;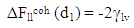 | (7) |
∆Fadh can be determined by several approaches, apart from the above surface free energy approach. The classical work of Hamaker [9] is very appropriate.To explain the concept of Hamaker Constants, use is made of the van der Waals explanation of the derivations of the ideal gas law;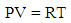 | (8) |
It was discovered that the kinetic energy of the molecules which strike the container wall is less than that of the bulk molecules. This effect was explained by the fact that the surface molecules are attracted by the bulk molecules (as in fig.3) even when the molecules have no permanent dipoles. It then follows that molecules can attract each other by some kind of cohesive force [10]. These forces have come to be known as van der Waals forces. van der Waals introduced the following corrections to Eq.(8);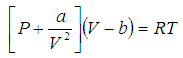 | (9) |
The correction term to the pressure, 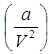 indicate that the kinetic energy of the molecules which strike the container wall is less than that of the bulk molecules. This signifies the earlier mentioned attraction between the surface molecules and the bulk molecules.
indicate that the kinetic energy of the molecules which strike the container wall is less than that of the bulk molecules. This signifies the earlier mentioned attraction between the surface molecules and the bulk molecules.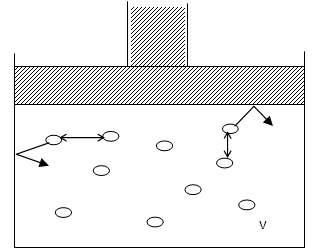 | Figure 3. Attraction of Surface Molecules by Bulk Molecules in a Container of Volume V [11] |
After the development of the theory of quantum mechanics, London quantified the van der Waals statement for molecules without a dipole and so molecular attraction forces began to be known as London/van der Waals forces [12]. London stated that the mutual attraction energy, VA of two molecules in a vacuum can be given by the equation; | (10) |
Where; h = Planck’s constant, υo = the characteristic frequency of the molecule, α = the polarizability of the molecule, H = their separationThe interaction of two identical molecules of a material 1 is shown in fig.4. | Figure 4. Interaction of Two Identical Molecules of Materials, 1 and Polarizability, α, at a Separation, H [11] |
Hamaker made an essential step in 1937 from the mutual attraction of two molecules. He deduced that assemblies of molecules as in a solid body must attract other assemblies. The interaction energy can be obtained by the summation of all the interaction energies of all molecules present as in fig.5. 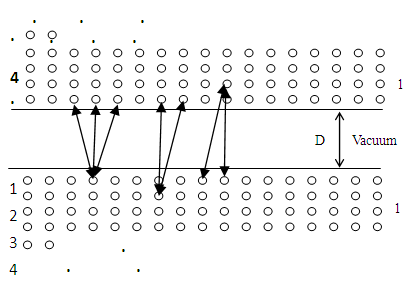 | Figure 5. Interaction of Two Semi-infinite Solid Bodies, 1 at a Separation, d in Vacuum [11] |
This results in a van der Waals pressure, Pvdw of attraction between two semi infinite (solid) bodies at a separation distance, d in vacuum;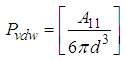 | (11) |
For a sphere of radius, R and a semi-infinite body at a minimum separation distance, d the van der Waals force, Fvdw of attraction is given by;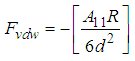 | (12) |
Where A11 is the Hamaker Constant 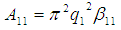 | (13) |
Where q1 is the number of atoms per cm3 and β11 is the London van der Waals constant. The corresponding van der Waals force between two dissimilar condensed bodies of given geometry with a separation distance, d can be determined. For the system under study, the interacting bodies are the macrophages, 1 and the bacteria, 2.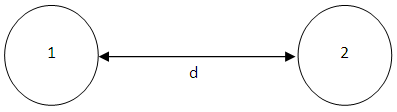 | Figure 6. Interaction of Two Semi-infinite Solid Bodies, 1 at a Separation, d in Vacuum [11] |
The van der Waals force between the macrophage, 1 and the bacteria, 2 is given by the relations: 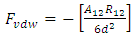 | (14) |
Where; 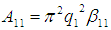 = Hamaker constant for macrophage.
= Hamaker constant for macrophage. 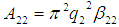 = Hamaker constant for the bacteria (M-TB).
= Hamaker constant for the bacteria (M-TB). 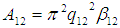 = Hamaker constant for both materias (i.e. macrophage and bacteria) Where:
= Hamaker constant for both materias (i.e. macrophage and bacteria) Where: 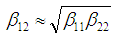 | (15) |
Thus the Hamaker constant becomes;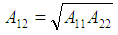 | (17) |
For a combination of two disimilar materials (i.e. macrophage, 1 and the bacteria, 2) with the gap between them filled with sputum as the medium 3, the combined Hamaker coefficient will be given by; 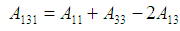 | (18) |
Also;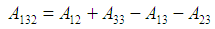 | (19) |
Rewriting these equations will give; 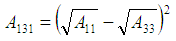 | (20) |
And;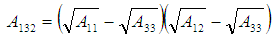 | (21) |
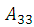 = Hamaker constant for sputum,
= Hamaker constant for sputum, 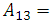 Hamaker constant between materials (i.e. macrophage and sputum)
Hamaker constant between materials (i.e. macrophage and sputum)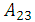 = Hamaker constant between material (i.e. the bacteria and sputum)The mean of all the values of the combined Hamaker coefficients, A132 gives an absolute value for the coefficient denoted by
= Hamaker constant between material (i.e. the bacteria and sputum)The mean of all the values of the combined Hamaker coefficients, A132 gives an absolute value for the coefficient denoted by 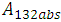 ;Thus the absolute Hamaker Coefficient
;Thus the absolute Hamaker Coefficient 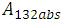 becomes;
becomes; 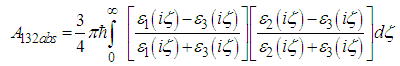 | (22) |
Applying the limits of integration (for the minimum and maximum values of A132 respectively), the absolute value for the combined Hamaker coefficient could thus be derived from the Lifshitz derivation for van der Waals forces as in Eq.(22) [13];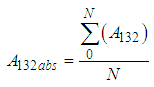 | (23) |
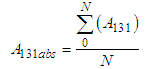 | (24) |
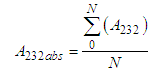 | (25) |
3. Research Methodology
3.1. Sample Collection
This research work involved collection of Sputum samples from twenty TB infected, twenty uninfected and twenty HIV/TB co-infected persons. The collected sputum samples were screened to determine the infection status using GeneXpert thus giving a total of sixty sputum samples from different individuals. The sputum samples were collected from Anambra State University Teaching Hospital (ANSUTH) Awka (formerly General Hospital Awka). Spot Specimens were used to ensure the freshness of the collected Sputum samples and to avoid the samples becoming lysed (spoilt). Storage facilities like refrigerators were also used to ensure that the samples were healthy enough so as to obtain good results.
3.2. Sample Preparation
The collected samples were loaded into GeneXpert Cartridge to determine if the sample is mycobacterium TB positive or negative. This helped to obtain and separate the positive and negative M-TB. The glass slides were prepared and smeared with the samples for absorbance measurements. The slide preparations and sample smearing were done at the same laboratory with proper safety measures to avoid being infected.The glass slide of 25.4mm x 76.2 x 1.2mm was used for the preparation of test surfaces. A dropper was used to draw each of the Sputum samples from the container and smeared carefully on a slide to ensure even distribution of the sputum samples on the slides. Three slides were prepared for each of the twenty sputum samples and smeared with the samples for absorbance measurements. The slide preparations and sample smearing were done at the same laboratory (Chest Clinic/Laboratory, Anambra State University Teaching Hospital, Awka). The samples were allowed to dry naturally at room temperature because exposing the prepared slides to the sun is likely to cause oxidation and the surface energy might be increased unconditionally. All the well prepared and dried surfaces were covered with microscopic cover slip, ready for the experiment.
3.3. Measurements
Absorbance measurements were done on all the positive and negative sputum components of all sixty samples (TB infected, TB uninfected, TB/HIV co-infected and macrophage sputum samples). A digital Ultraviolet Visible Spectrophotometer (UV/VIS MetaSpecAE1405031Pro) was used in the measurements. The measurements of absorbance and transmittance were done at Bioengineering Labouratory of the department of Mechanical Engineering, Nnamdi Azikiwe University, Awka. The absorbance values of the samples were measured over a range of wavelength spanning between 230 and 950 Å. The data collected were used in calculating the Hamaker coefficients using the Lifshitz formula.
4. Results and Analysis
4.1. Relevant Mathematical Applications to the System
To be able to use the absorbance data to calculate the Hamaker coefficients, some relevant equations are required as presented: from the information of light absorbance, reflection and transmittance, it could be seen that;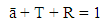 | (26) |
Where; ā is absorbance, T is transmittance, and R is reflectance.Also, from the information of light absorbance and transmittance;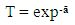 | (27) |
With the values of ā determined from absorbance experimental results, and substituting the values of ā into Eq. (27) to obtain T, R could easily be derived by substituting the values of ā and T into Eq.(26).The value for the refractive index, n was found employing the mathematical relation [14-15];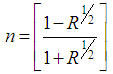 | (28) |
A value for the extinction coefficient, k is obtained from the equation;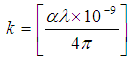 | (29) |
Where; α is the absorption coefficient defined as follows;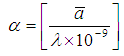 | (30) |
Substituting the value, 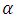 of Eq. (30) into Eq. (29);
of Eq. (30) into Eq. (29);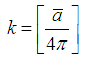 | (31) |
The dielectric constant, ε could thus be given by the formula [15-16]For the real part; 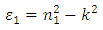 | (32) |
For the imaginary part; 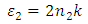 | (33) |
With these values, it is possible to use the approximate approach to determine A11.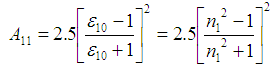 | (34) |
This gives a value to the Hamaker constant A11, and by extension to other Hamaker constants A22 and A33.Thus, the Hamaker coefficient, A132 could readily be gotten from the relations as in Eq. (21);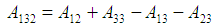 Alternatively;
Alternatively; 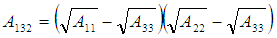 Eqns. (22), (23) and (24) was used to obtain for each absolute value of Hamaker coefficients (A131abs, A132abs, A232abs). MAtlab software tools were used in computation. This involved the numerical integration of eqn. (22) for each wavelength from 230 to 950 for all the twenty samples in each category. The results are presented in table 1.
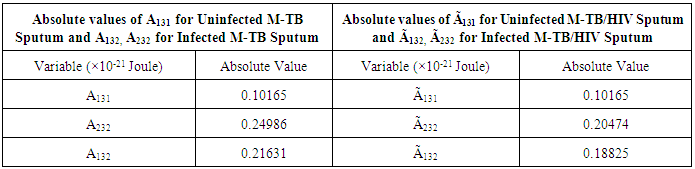
Eqns. (22), (23) and (24) was used to obtain for each absolute value of Hamaker coefficients (A131abs, A132abs, A232abs). MAtlab software tools were used in computation. This involved the numerical integration of eqn. (22) for each wavelength from 230 to 950 for all the twenty samples in each category. The results are presented in table 1.Table 1. Computation of the absolute values of Hamaker Coefficients for Uninfected and Infected Sputum
 |
| |
|
Table 1; reveal that the surface energy of the macrophages as computed interms of Hamaker coefficients is less than the surface energy of the M-TB, M-TB/HIV. This result also shows that the surface energy of the M-TB/HIV macrophage is less than that of M-TB macrophage. HIV has the tendency to reduce the energy with the consequence of increased viral loads and decreased immune systems. TB is an opportunistic disease and in presence of HIV, the consequence is grievous. Hence for A132 > 0, A131(macropage) < A232(M-TB/HIV). Fig.7 reveals the pattern of the average combined Hamaker coefficients, A132, A131 and A232 for the sputum samples with clear peak values occurring at various wavelengths. The peak average values of A132 and A232 occur at wavelength of 320Å with values of 0.30968x10-21J and 0.18609 x10-21J respectively, while the peak average value of A131 occurs at wavelength of 290Å with value of 0.03074. Energy level increases in average combined Hamaker coefficients (A132 and A232), which is the infected Hamaker coefficients as against the decreased energy level of the uninfected average combined Hamaker coefficient, A131. This is quite a significant phenomenon which explains away the fact of infection.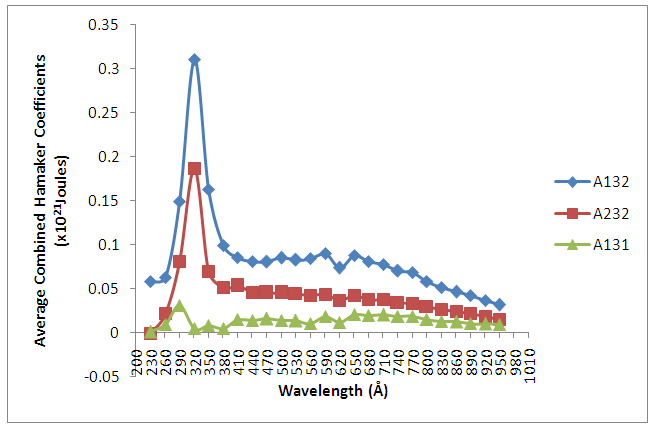 | Figure 7. Variation of Average Combined Hamaker Coefficients, A132 A131 and A232 with Wavelength, λ (Å) for the M-TB infected Sputum Samples |
4.2. Computation of Surface Free Energy and Change in Free Energy of Adhesion
For all given combinations, it is possible to express the van der Waals force of cohesion which is the force of attraction between similar particles in a substance, just as the surface energy or energy of interaction is a function of van der Waals force of adhesion which is the force of attraction between different particles suspended in a liquid medium.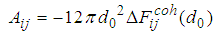 | (35) |
And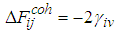 | (36) |
Combining Eq. (35) and Eq. (36):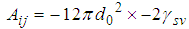 | (37) |
Hence;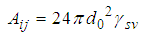 | (38) |
The surface free energy is given thus; 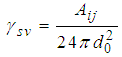 | (39) |
The minimum distance do between the same particles is given as: 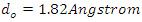 [17].Also;
[17].Also;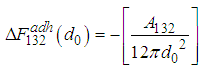 | (40) |
Equation (39) with values of computed  were use for the computation of γsv (see Tables 2 and 3)
were use for the computation of γsv (see Tables 2 and 3) Table 2. Computed values of surface energies γsv of the M-TB Sputum Interacting Systems
 |
| |
|
Table 3. Computed values of surface energies γsv of the M-TB/HIV Sputum Interacting Systems
 |
| |
|
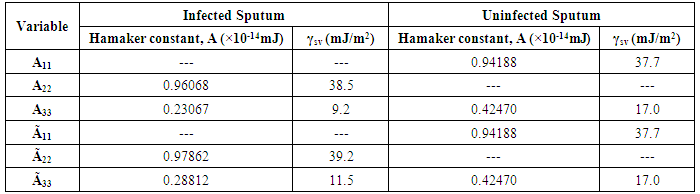
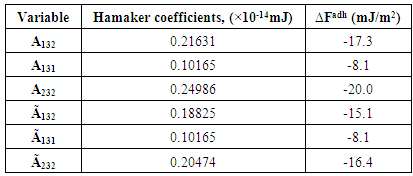
Since the surface energy is a measure of workdone on the surface. Table 2 shows the surface energy of the M-TB is greater than the surface energy of the sputum. Also, the surface energy of the uninfected sputum 17.0mJ/m2 was apparently reduced to 9.2mJ/m2 when M-TB attacked the human system. Consequently, the disease incidence lowers the surface energy of the infected sputum as shown in table 2. This in effect indicates that M-TB has a surface energy reducing capacity in line with the findings by Ozoihu [18] for HIV – Lymphocytes interactions.Table 3 shows that the surface energy of the M-TB/HIV is greater than the surface energy of the sputum. Also, the surface energy of the uninfected sputum 17.0mJ/m2 was in fact reduced to 11.5mJ/m2 when M-TB/HIV co-infection attacked the human system. As a result, the disease incidence lowers the surface energy of the infected sputum as shown in table 3. This in effect indicates that M-TB/HIV has a surface energy reducing capacity tending to make the surface of the bacteria (sputum) more hydrophobic. From table 3; the following deductions are made: Surface free energies of infected sputum components are lower than the uninfected, M-TB infection has the surface energy reducing capacity (i.e. reduces the work done on the surface), It is well identified that M-TB/HIV attacks the macrophage; the reduction (difference on infected and uninfected) in surface free energies of Sputum could be as a result of its presence in the sputum.The surface free energies described in tables 4 and 5 are used to determine the free energy of adhesion. When the change in free energy of adhesion is negative; adhesion is thermodynamically favorable. Adhesion is therefore governed by attractive van der Waal forces. When M-TB or M-TB/HIV co-infection affixes itself to the surface of the macrophage in a liquid medium, there is the tendency of the bacteria to be engulfed by the macrophage cells causing their destruction. Thus increased adhesion may lead to more depletion of macrophage cells. The adhesion of the bacteria on the cell will lead to penetration into the macrophage. Such a penetration will cause replication of bacteria and destruction of macrophage. What is required is for this attachment not to occur. Results obtained (table 5) give the following deductions: The change in free energies of adhesion is all negative indicating that the net van der Waals forces are attractive, the change in free energies of adhesion is higher for infected M-TB/HIV than infected M-TB. In order words, presence of HIV increases the change in free energy of adhesion and hence tendency for increased attack, Hamaker coefficients are all positive suggesting van der Waals forces are attractive as negative free energy of adhesion.Table 4. Comparison of the values of Surface Free Energy γsv of the M-TB and M-TB/HIV Infected and Uninfected Sputum
 |
| |
|
Table 5. Computation of Change in free energy of adhesion, ∆Fadh (mJ/m2)
 |
| |
|
5. Conclusions
This research work on M-TB – Human sputum interaction has further buttressed the place of the relevance of engineering thermodynamics or at least quasi- thermodynamics in offering suggestions and possible solutions to various scientific and biological processes. The indispensible fact of inter-relativity of diverse disciplines and the prime place of engineering to this conclusion cannot be overemphasized. This in some way goes to speak of concurrent engineering and its vital role in the twenty first century research. The results obtained from absorbance measurements were used to calculate the variables such as transmittance T, reflectance R, refractive index (real and imaginary) n, extinction coefficient K, absorption coefficient α, dielectric constants (real and imaginary) εij, Hamaker constants Aij and Hamaker coefficients A132. These results were used to predict the interaction that occurs between M-TB/HIV co-infections. This prediction was based on the concept of van der Waals attractive forces and absolute Hamaker coefficient whose negative and positive values respectively indicate attraction.The first round of calculations of surface free energy and change in free energy of adhesion for both M-TB/HIV infected and uninfected sputum provided an easy approach to the estimation of Hamaker coefficients for the interacting systems. The presence of M-TB/HIV however, reduces the work done on the surface. The surface energy decreases when infected by the M-TB/HIV and thus, M-TB/HIV has the capacity to lower the surface energy. The decrease in surface energy for infected sputum and mostly for macrophage is a confirmation that macrophages are mostly attracted by the M-TB. Absence of M-TB/HIV however, increases the surface energy. The change in free energy of adhesion increases when M-TB infection affixes itself to the surface of the macrophage. This means that presence of M-TB/HIV increases van der waals attractive force and mostly for infected macrophages. The energies of interactions expressed as Hamaker coefficients are all positive and this also validates the claim that attraction occurs between HIV and blood during infection as observed also by Ozoihu [18]. This research concludes that there is a prospect of finding remedy for the M-TB/HIV deadly disease if further work towards defining the conditions of the system that could render the absolute combined Hamaker coefficient negative (block the association of the bacteria and macrophage) and the additive(s) to the system (in form of drugs) as the intervening medium that could accomplish this condition.
References
| [1] | World Health Organization (WHO), 2005, Tuberculosis, WHO Information: Fact Sheets. http://www.who.int/mediacentre/factsheets/fs104/en/index.html, Retrieved 24-11-13. |
| [2] | World Health Organization (WHO), 2011, Global HIV/AIDS Response Epidemic update and Health sector progress towards Universal Access: http://whqlibdoc.who.int/publications/2011/9789241502986-eng.pdf. |
| [3] | De Souza M. V. N., 2006, Recent patents on Anti-infective Drug Discovery, 1: 33 – 34. |
| [4] | Gonzalez-Juarrero M., Turner O. C., Turner J., Marietta P., Brooks J. V., Orme I. M., 2001, Temporal and Spatial arrangement of lymphocytes within lung granulomas induced by aerosol infection with mycobacterium tuberculosis. Infect. Immun. 69: 1722 – 1728. |
| [5] | Nunes J. E. S., Ducati R. G., Breda A., Rosado L. A., De Souza B. M., Palma M. S., Santos D. S., Basso L. A., 2011, Molecular, kinetic Thermodynamic and Structural analysis of mycobacterium tuberculosis hisD-encoded metal-dependent dimeric histidinol dehydrogenase (EC1.1.1.23). Archives Biochemistry and Biophysics, 512: 143 – 153. |
| [6] | Achebe C.H., Omenyi S.N., Manafa O.P., Okoli D., 2012, Human Immunodeficiency Virus (HIV)-Blood Interactions: Surface Thermodynamics Approach. Proceedings of the International Multi-Conference of Engineers and Computer Scientists 2012, Hong Kong, 136 – 141. |
| [7] | Achebe C. H., Omenyi S. N., 2013, The Effects of Human Immunodeficiency virus (HIV) Infection on the Absorbance characteristics of Different Blood Components. International Journal of Engineering Science Invention, 2(5), 53 – 61. |
| [8] | Omenyi S. N., 1978, Attraction and Repulsion of particles by Solidification Fronts” PhD Dissertation, University of Toronto. p.23, 33, 34. |
| [9] | Hamaker, H.C., 1937, Physica, 4: 1058. |
| [10] | van der Waals, J.D., 1873, Thesis, Leiden. |
| [11] | Visser, J., 1981, Advances in Interface Science, Elsevier Scientific Publishing Company, Amsterdam, 15: 157–169. |
| [12] | London F., 1930, Physics, 63: 245. |
| [13] | Dzyaloshinskii, I.E., Lifshitz, E.M., et al 1961, Advanced Physics.10:165. |
| [14] | Robinson, T.S., 1952, Proc. Phys. Soc. London 65B910 |
| [15] | Chukwuneke, J. L., 2015, “Surface Energetics of Mycobacterium Tuberculosis (M-TB) – Macrophage Interactions” Ph.D Dissertation, Nnamdi Azikiwe University, Awka, Nigeria. |
| [16] | Viser J., 1981, Advances in interface, Elsevier Scientific publishing company, Armsterdam, 15: 157 – 169. |
| [17] | Charles, Kittel, 1996, Introduction to Solid state Physics, 7th Ed., John Willey and sons Inc. New York, p.308. |
| [18] | Ozoihu, E.M., 2014, Human Immunodefficiency Virus (HIV)-Blood Interactions: Contact Angle Approach, PhD. Dissertation, Nnamdi Azikiwe University, Awka, Nigeria. |

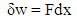

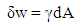
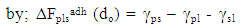
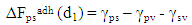
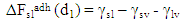
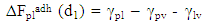
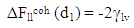
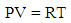
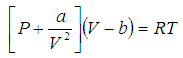
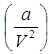 indicate that the kinetic energy of the molecules which strike the container wall is less than that of the bulk molecules. This signifies the earlier mentioned attraction between the surface molecules and the bulk molecules.
indicate that the kinetic energy of the molecules which strike the container wall is less than that of the bulk molecules. This signifies the earlier mentioned attraction between the surface molecules and the bulk molecules.
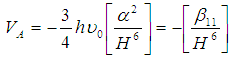


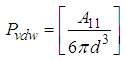
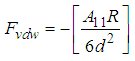
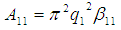

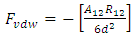
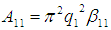 = Hamaker constant for macrophage.
= Hamaker constant for macrophage. 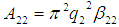 = Hamaker constant for the bacteria (M-TB).
= Hamaker constant for the bacteria (M-TB). 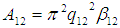 = Hamaker constant for both materias (i.e. macrophage and bacteria) Where:
= Hamaker constant for both materias (i.e. macrophage and bacteria) Where: 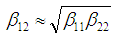
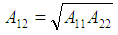
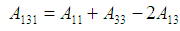
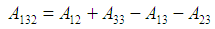
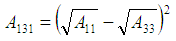
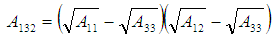
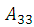 = Hamaker constant for sputum,
= Hamaker constant for sputum, 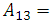 Hamaker constant between materials (i.e. macrophage and sputum)
Hamaker constant between materials (i.e. macrophage and sputum)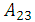 = Hamaker constant between material (i.e. the bacteria and sputum)The mean of all the values of the combined Hamaker coefficients, A132 gives an absolute value for the coefficient denoted by
= Hamaker constant between material (i.e. the bacteria and sputum)The mean of all the values of the combined Hamaker coefficients, A132 gives an absolute value for the coefficient denoted by 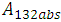 ;Thus the absolute Hamaker Coefficient
;Thus the absolute Hamaker Coefficient 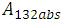 becomes;
becomes; 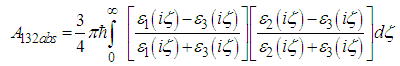
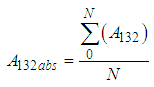
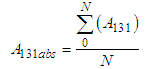
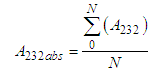
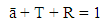
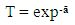
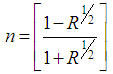
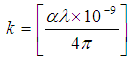
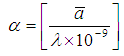
 of Eq. (30) into Eq. (29);
of Eq. (30) into Eq. (29);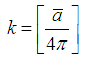
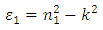
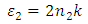
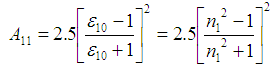
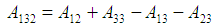 Alternatively;
Alternatively; 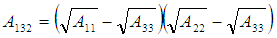 Eqns. (22), (23) and (24) was used to obtain for each absolute value of Hamaker coefficients (A131abs, A132abs, A232abs). MAtlab software tools were used in computation. This involved the numerical integration of eqn. (22) for each wavelength from 230 to 950 for all the twenty samples in each category. The results are presented in table 1.
Eqns. (22), (23) and (24) was used to obtain for each absolute value of Hamaker coefficients (A131abs, A132abs, A232abs). MAtlab software tools were used in computation. This involved the numerical integration of eqn. (22) for each wavelength from 230 to 950 for all the twenty samples in each category. The results are presented in table 1.
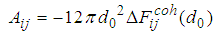
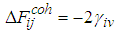
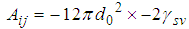
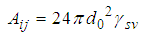
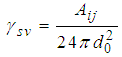
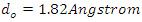 [17].Also;
[17].Also;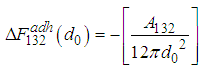
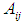 were use for the computation of γsv (see Tables 2 and 3)
were use for the computation of γsv (see Tables 2 and 3)  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML



