1. Introduction

Life can be explained as success of fundamental objectives (fitness, minimum entropy), which are present in nature and in society as self-organized and evolutionary forces of competition, cooperation and coopetition. Pure competition generates winners and losers, pure cooperation generates organized systems, and coopetition gives origin to self-organized and intelligent systems. Persistence and search of fundamental objectives maintains life, guarantees and justifies species existence. In synthesis, it is not enough to explain life and society from a unilateral perspective, that is to say, absolute competition or absolute cooperation. Self-organization is the equilibrium between cooperative and competitive equilibria, we will understand for self-organization the equilibrium of equilibria, while coopetition is simply simultaneous presence of cooperation and competition.Firstly, because winners are a very few number in society, let us analyze soccer, where less than 1% are stars, the other, although necessary so that winner shines are not remembered. Also, let us analyze science, where in each discipline of knowledge only one obtains the Nobel Prize, less than one for thousand. Finally, let us analyze politics, sometimes in many years only a true leader arises, less than one for million. The word "loser" should be redefined or at least, it is necessary to recognize that exist several loser types: the indefatigable fighter that knows that success won´t arrive possibly, the fighter for conviction who knows that daily and well carried out work produces happiness.

What happen in society? Have we forgotten that so that a winner exists it is necessary a competition. On the other hand so that an organized system such us neural networks exist motor is cooperation. Nevertheless, external pressure that propitiates evolution of species is competition, but, internal changes of each species are guided by cooperation and organization, that is to say, competition unchains cooperation, in logical language: external competition→ internal cooperation and internal cooperation → internal organization, with permit us to conclude: external competition→ internal organization. The previous virtuous cycle should be closed, the question is where?

Secondly, according to Evolutionary Game Theory existence of winners and losers has a cause called asymmetry (differences in weight, experience, size, resistance, adaptability) among players. Players can be cells, animals, or human beings. A war or conflict takes place by own dynamics of by every day relationships between players, even they do cooperative activities absolutely.

Said otherwise, daily and strategic relationship among players could produce competitions and conflicts. In synthesis, cooperation of different players can also originate competition, in logical language: internal cooperation→ external competition or external cooperation→ external competition. We already have some elements that allow us to represent life cycle. The symbol→ indicates implication. To summarize, we obtain the following implications of competition side:

if external competition → internal cooperation

and internal cooperation → internal organization

then external competition → internal organization

From cooperation perspective, we have some implications that indicate as competition is generated among isolated players or among member player of a grouping.

Internal cooperation → external competition

or external cooperation → external competition

Integrating and giving generality to previous implications, we can write:

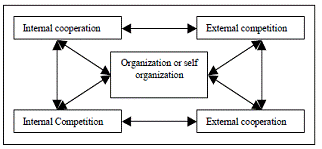Figure 1. Relationship among systems strategic elements: organization is the result of internal cooperation, internal competition, external cooperation and external competition.

In the previous graph, arrows not only indicate relationship among parts but also indicate causation and implication, in other words, it is the continuous evolution of cooperation toward competition and of competition toward cooperation. Certain systems of nature and society will be more cooperative than other, although also will exist completely competitive systems. Moreover, competition and cooperation degree is function of fundamental objectives, for example, cooperation to solve common problems or competition to solve individual problems.

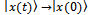Fundamentally, the previous graph indicates existence of two main properties: reversion and evolution. The first one is related with reversible processes, and represented by a biconditional and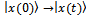, while the second is related with quantum evolution operator, Ut.

In order to put in mathematical language, we can assume that a system is in an initial quantum state named 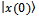and after of cooperative and competitive interactions it arrives to a final state named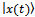: Using evolution operator, Ut it is possible to represent the final state 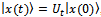, equations (9), (10) and (11). Also, taking into account unitary operator properties, we can write reversion property as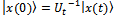. Finally, invariant unitary transformations let invariant the norm .

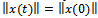Thirdly, in a sequence of asymmetric wars, frequent winner becomes eternal, giving as a result that winners are minority and that losers are majority. The solutions of cooperative and competitive equilibria are different, because objectives of each of them are different. Competitive equilibria objective is utility maximization of every player, as long as fundamental objective of cooperative equilibrium is organization, here, we have a difference in Nash conception of cooperative equilibrium. Self-organization is the equilibrium of equilibria and it implies coordination of actions among each one of the components of a system.

To achieve maximum coordination among players it is required interconnection and interdependence, that is to say, correlation (entanglement) of players and strategies.

Summarizing, Darwin Natural Selection Theory explains survival of the most capable, using as fundamental element external competition among species, which can be understood as an equilibrium dimension. As long as Molecular Biology studies both entropy minimization and increase of interior complexity. Increase of complexity is related to organization and internal cooperation. When internal cooperation and external competition are equilibrated then take place self-organization and intelligence. Therefore, self-organization is the equilibrium of cooperative and competitive equilibria, and cancer dynamics is self-organization lost among cells.

1.1. Cancer, Competition and Cooperation

We will carry out a revision of some topics involved with cancer studies such us genetic predisposition toward cancer, modern theories of origin and cancer treatment, and game theory tools used to approach and to model cancer dynamics, see Coller, H, Sang Liyun and Roberts (2006), RA Eeles, DF Easton, BAJ Ponder and C Eng (Editors, 2006), C.C. Maley, B.J. Reid, S. Forrest (2004), I.P.M. Tomlinson (1997), Seimiya, H (2006).

Advances in human genetics have given substance to the old ‘experiential’ knowledge of health problems that run in families and the risks of being affected by the same condition. However, this field is not only the province of medical and biological research but is also a minefield of ethical concerns, issues for the wider society, and potential adverse psychological effects on individual patients and families. There is a fuzzy border between research and care, with potentially huge cost implications. Inherited cancer syndromes can well be regarded as an example of so-called ‘post normal science’ where facts are uncertain, values in dispute, stakes high, and decisions urgent. ‘Genetic Predisposition to Cancer’ is welcome, for many surveys show that family and general practitioners and even some specialists have a serious lack of knowledge in this area.

Taking into account that in cancer treatment, it is considered universally that a person with cancer is clinically cured, when had destroyed all cancerous cells (cellular death) or when has been cut or suspended abnormal reproduction of these cells. In our opinion, a low entanglement according to the outline of Hameroff, S.R (2004) would suspend abnormal reproduction of cancerous cells.

Hameroff, in his excellent article, bases its proposal “A new theory of the origin of cancer: quantum coherent entanglement, centrioles, mitosis and differentiation”, using as base previous works carried out together with Penrose, Hagan, Woolf, Tuszynski and others: Hameroff, E and Watt, R (1982), Hameroff, S.R and Penrose, R (1996), Hameroff, S.R and Penrose, R (2003), Nancy J.Woolf and Stuart R. Hamero¤(2001), S. Hagan, S. R. Hameroff,2 and J. A. Tuszynski (2002), Stuart Hameroff , Alex Nip, Mitchell Porter, and Jack Tuszynski (2002).

Of analyzed papers, we have extracted main implications of cancer dynamics and its relationship with cooperative and competitive equilibria, showing an indissoluble dependence between Game Theory and cancer cell treatment.

• It is suggested in Hameroff´s theory that normal mitosis is organized by quantum entanglement and quantum coherence among centrioles. In particular, quantum optical properties of centrioles enable entanglement in normal mitosis which ensures precise mirror-like activities of mitotic spindles and daughter chromatids, and proper differentiation, communication and boundary recognition between daughter cells.

• Defects in the proposed mitotic quantum entanglement/coherence can explain all aspects of malignancy. Analysis and duplication of quantum optical properties of normal cell centrioles could possibly lead to laser-mediated therapeutic disruption and/or reprogramming of cancerous tumors as well as abundant, ethical production of stem cells.

• Current therapies for cancer are generally aimed at impairing mitosis and are thus severely toxic. Many cancer drugs (vincristine, taxol etc.) bind to microtubules and prevent their disassembly/assembly required for formation and activities of the mitotic spindles. In addition to generalized toxicity due to impairment of non-mitotic microtubule function, partial disruption of mitosis can cause further aneuploidy. Radiation is also a toxic process with the goal of impairing/destroying highly active malignant cells more than normal cells. Recognizing centrosomes as the key organizing factor in mitosis.

Conjecture 1 Definitively, one entanglement type should exist inside cellular reproduction process, because it is of type mirror-like. Also, it is probable that different entanglement types exist with TUBULINS and another entanglement type with CENTRIOLES, where each one would have their own function. For example, it seems that a correct tubulins entanglement is related with symmetry, in mitosis process. Moreover, it seems that a correct centrioles entanglement is related to chromosomes distribution in healthy cells.

• Centrioles are the specific apparatus within living cells which trigger and guide not only mitosis, but other major reorganizations of cellular structure occurring during growth and differentiation. Somehow centrioles have command of their orientation in space, and convey that information to other cytoskeletal structures.

• There are a number of questions regarding mitosis, but one compelling issue is how all the intricate processes are coordinated in space and time by centrioles to generate a geometric structure that maintains itself at steady state.

Conjecture 2 The problem of directional or selective entanglement should be explained to depth, especially, with objective of knowing if entanglement is given among healthy cells, among cancerous cells or it is a mixed outline (cancerous and healthy).

Hameroff believes that is more feasible centrioles entanglement than tubulins entanglement. If we consider a single entanglement type, for example, of tubulins then it is possible to obtain centrioles entanglement. If we know that centrioles are in the interior of a dense substance of free electrons, then it would be possible to use resonant microwaves with frequencies in the range of transition of non-allowed quantum states. This would drive to that free electrons enter in a state of momentary non-equilibrium of milliseconds order. Therefore, if process of resonant microwaves stays, then we could create little by little, centriole paired entanglement.

• If each tubulin can be in one of two possible states, each centriole could be in one of 230,000 possible states. Considering variations in isozymes and post-translational modifications, each tubulin may exist in many more than two possible states (e.g. 10), and centrioles may therefore exist in up to 1030,000 possible states─easily sufficient to represent each and every possible phenotype. But regardless of their specific complexity, replicated centrioles would be in identical (or complementary, i.e. precisely opposite) entangled states. How could entanglement actually occur? Centrioles are embedded in an electron dense protein matrix (“pericentrin”) to which mitotic spindle microtubules attach; the opposite ends of the spindles bind specific chromatids via centromere/kinetochores. The cen- triole/pericentrin (“centrosome”) and spindle complex are embedded in protein gel and ordered water so that the entire mitotic complex may (at least transiently) be considered a pumped quantum system (e.g. a Fröhlich Bose-Einstein condensate) unified by quantum coherence.

• Thus, despite being largely water, cell interiors are not “aqueous” but rather a crystal-like structure. Perhaps most importantly, experimental evidence shows that electron quantum spin transfer between quantum dots connected by organic benzene molecules is more efficient at room temperature than at absolute zero, see Hameroff, S.R (2004, pag 131).

Remark 3 It is interesting to present asymmetry (imperfect entanglement) of mitosis process as cause of cancer, eliminating current paradigm which present asymmetry as a result of cancerous cell action. In this point, it is necessary to be cautious, because according to Hameroff ´ s theory perfect entanglement is equivalent to symmetry. However last advances of Quantum Computing indicate that perfect entanglement doesn´t always exist.

Remark 4 Great advance to science that make Penrose-Hameroff, when showing and studying storage capacities, prosecution and transport of Information in the tubulins open new investigation goals, because they not only affirm that cell brain are centrioles but also that they control whole mitosis.

Conjecture 5 According to Y. Mansury, M. Diggory, T.S. Deisboeck (2006), we can conclude that due to narrow connection among genotipo-fenotipo, it is possible to act in cancer therapies for two fronts toward genotype or toward phenotype. Also, we can affirm that entanglement is directed toward phenotype as long as certain chemotherapy products have implications in genotype. Moreover, it is evidenced that some chemical compounds have similar behaviors to tumor suppressor genes.

Axiom 6 It is possible to evaluate cancer dynamics as like cooperation and competition forces, where cooperation forces wants to restore the equilibrium lost due to cancer action.

In words of, Y. Mansury, M. Diggory, T.S. Deisboeck (2006) "The interactions among tumor cells and between cells and environment create the diametrically opposing forces of cooperation and competition, which can lead to nonlinear dynamics and complex spatial pattern. Cooperation emerges when a group of tumor cells together generate a synergistic effect in the form of higher fitness levels than those of individually isolated cells"

To evaluate cancer dynamics as cooperation and competition forces has much sense, because all cells has repair mechanisms in case of chromosomal damage in the DNA. Success of this repair process would be related to interaction between genotype- environments. Also, it is important to clarify that a mechanism repair of cancerous cells are less effective than that one of a healthy cell. This last evidence constitutes the base of a radiotherapy treatment.

This paper pursues three concrete objectives; therefore, we will use bibliography that allows us to explain, to model and to open new horizons in cancer treatment: 1. - to demonstrate that cancer is the result of equilibrium lost among healthy cells. 2. - to evidence the use of constructive entanglement and cooperation, those which they can restore biological equilibrium lost, even thought, healthy cells can increase cancer propagation speed, for it information plays an important role to block a possible destructive entanglement. 3. - to present empirical and theoretical evidences that authorize us to use cooperative and competitive game theory in the fight against cancer, in a specific way, to prove that in a strategic interaction, flow of information, and feeding devices among healthy or sick cells are governed by laws of Game Theory and Complex Systems.

Theoretical foundations of cooperative and competitive games can be found in: Hammerstein, P, Ed (2003), Hammerstein and Selten (1994), Myerson, R. (1991). Complex systems permit us to study systems where there is common objectives such us entropy reduction, cooperation and self-organization, these last concepts are studied to depth in: Bar-Yam, Y (1997), Boccara, N (2004 ), Jiménez, E and Moya, D (2005), Jiménez, E.H (2003), Lambert A, Zamir Sh, Zwirn H (2007).

2. Attrition between Opponents and Prisoner’S Dilemma between Partners

In a Cancer Treatment game, there are manifested simultaneous characteristics internal cooperation and external competition. Said otherwise, it is the coexistence of cooperative and non-cooperative games, although, in theory, each team (tumor cells and healthy cells) exclusively should cooperate to the interior, but in reality, certain individualities are presented, not only due to cancer cells but also healthy cells. It is important to notice that interaction between team partners is represented by prisoner’s dilemma bimatrix game, while interaction between opponents is represented by attrition.

This reasoning is valid, because, attrition utilities can have negative values, something completely appropriate with reality, because in certain occasions result of interaction between two opponents take place serious physical lesions. In interaction between partners, modeling as prisoner’s dilemma, strategic interaction is manifested as cooperate or not, without arriving to aggression degree, which is manifested explicitly in interactions between opponents named attrition game; see Hammerstein and Selten (1994), Myerson, R. (1991), Y. Mansury, M. Diggory, T.S. Deisboeck (2006), I.P.M. Tomlinson (1997).

2.1. A Cancer Treatment will never be Successful without Cooperation of the Healthy Cells

Cooperation is not only result of coordination but also is result of correlation of strategies. This correlation of strategies has a name in Quantum Computing Sciences, entanglement. Entanglement indicates that if two players, taken two at two are correlated, then without necessity of information emission or messages, the action of one determines the action of another. A correlation of three players can exist in a game. Although, Cancer Treatment is a sequential process, where a player sends information to other, the second to another and so forth, it finishes in an action one to one. The final result of entanglement can be a chain of actions and during the whole cancer treatment game is guided by an invariant common objective, that is to say, to win the match, always advancing toward the destruction cancer cells.

Therefore, if healthy cells are correlated two at two, then the probability of obtaining a cooperative result or of team is bigger, see C.C. Maley at all (2004), C.C. Maley, B.J. Reid, S. Forrest (2004).

In short, the main theorem of this article shows that correlated cells (entangled) always increase cooperation probability in a dynamic game; see entanglement in Einstein, A. Podolsky, B and Rosen, N (1935), Eisert J; M Wilkens, Lewenstein (1999), Jiménez, E.H (2003). The word correlated in language of cancer treatment means, a cohesive team, where cells interact among them; moreover, they know and develop their skills and experience. We understand correlation like as correspondence or reciprocal relationship between two or more cells; these players are game strategies (cells). A relationship is also a correspondence between players or strategies, but without reciprocity characteristic, which is inherent to cooperation.

2.2. Individualities a Perfect Sub Game

A player endowed with unique qualities, defines a perfect sub game, in which, the objective of a team should be completed, to transfer cytotoxins and to win. To facilitate understanding of this paper, it has been structured in the following way: Introduction settles down in a qualitative way theoretical contributions of quantum correlation, asymmetry, self-organization, cooperation and competition. Quantitative section, presented through the entanglement operator, establishes necessary theorems of correlation like fundamental element of cooperation. Conclusions give an integral structure to this paper, because from a practical perspective, we introduce a series of appropriate advises for cancer treatment research.

3. Methods

3.1. Cooperation Operator

In order to describe a game between two teams, it is necessary to introduce the concept of dynamic strategy, which is represented by a player. Likewise, each couple of players defines a symmetrical bimatrix sub game. The interaction between the two teams is given by means of traditional strategic outline; therefore, interaction between each couple of strategies is given by an outline of a symmetrical bimatrix game (prisoner’s dilemma or attrition). For partners (cells of oneself team), interaction is of prisoner’s dilemma type, where sub strategies are {cooperate or non-cooperate}. While, interaction between opponents (cells of a contrary team) is of attrition type, where sub strategies are {attach or defend}. In summary, attrition and prisoner's dilemma can be formalized as a two-player quantum game. Traditional illnesses such as cancer and AIDS, in which, it is manifested internal cooperation between partners and external competition between opponents obey the mathematical formalization here presented.

Let Γ = (I, S, ν) be that represents a finite game in strategy form, with I the set of teams of cardinality two; then every team is noted 1; 2 Є I. The finite set Si of cardinality m1, m2 Є N is the set of pure strategies of each team 1; 2 Є I, (sij)j Є Ji Є Si, Ji = {1, …, mi} and S = ПiЄI Si designates the set of profiles in pure strategies of the game with s Є S an element of that set. The function ν: S → Rn associates to every profile s Є S the vector of utilities ν(s) = (ν1(s), νn(s)), where νi(s) designates the utility of the team i facing the profile s. If mixed strategies are allowed then we have:

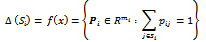The unit simplex of the mixed strategies of team i є I. We will note pi = (pij)jєI. The set of ´profiles in mixed strategies is the polyhedron ∆ with ∆ = ПiЄI ∆(Si) and p є ∆ a point of ∆, where p = (p1j, …, pnj).

The function u: 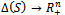associates to every profile in mixed strategies, (p є ∆) the vector of expected utilities 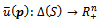such that 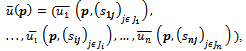, where 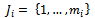and 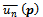is the expected utility of the player

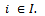Every 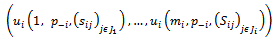represents the player’s preferences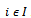. The triplet 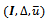designates the extension of the game Γ to the mixed strategies.

If the payment function is de.ned by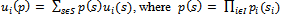, and if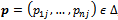, then we get Nash’s equilibrium if, and only if, for all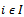, and all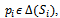, the next inequality holds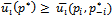, where 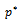is an optimal strategy.

A two-player quantum game Γ = (H; p; SA; SB; PA; PB) is completely specified by the underlying Hilbert space H of the physical or economical system, the initial state, 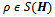where S(H) is the associated state space, the sets SA; SB of permissible quantum operations of the two-players, and the utility functional 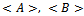which specify the utility for each player.

A quantum strategy 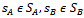is a quantum operation, thet is, completely positive trace-preserving map mapping the state space on itself; Eisert J; M Wilkens and Lewenstein (1999).

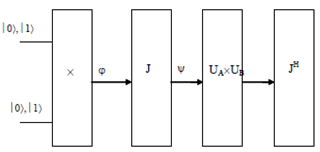Figure 2. Evolution of initial state function

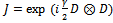In the initial stage of the game (Figure: Evolution of initial state function), every couple of partners are non-correlated, they are in one of the four initial states |00>, |11>, |01>, |10>. We apply entangled operator to every couple of partners. This operator correlates sub strategies of every player, given as result, one of the four states of maximum entanglement 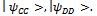Maximum entanglement is obtained when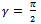, whereas, no-entanglement is when 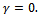At least At least from a theoretical point of view, using entangled operator 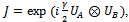exit several forms to obtain correlated players.

Without losing generality and in order to facilitating explanation, we have selected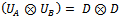, where the matrix D is a particular case of an evolution operator 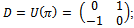see Eisert et al (1999), Machiavello et al (2000), Nielsen and Chuang (2000).

Definition 7 Initial states are |00>, |11>, |01>, |10> and they are obtained as tensor product of vectors |0>, |1>, where:

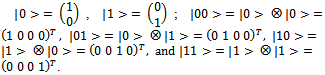Let 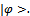be an initial state function, build as lineal superposition of fundamental states.

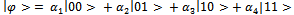(1)

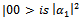Where the probability of get the state, and in a similar way

Let be Hilbert spaces with basis The tensor product of spaces 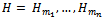is denoted by. Using Dirac’s notation, space H has ordered elements; Hirvensalo. M (2001).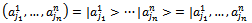

(1.1)

basis, thus H has dimension As in the case of classic and probabilistic systems, the basis states of the compound system H can be thought of elements. It is natural to represent the general state of the compound system as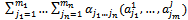, where 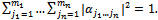We say decomposable system iff

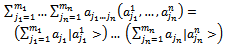(1.2)

Defnition 8 We say that the compound system is entangled iff it is not decomposable.

Defnition 9 Entanglement operator J permits us to correlate sub strategies of each player.

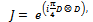(2)

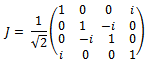Applying entanglement operator on initial state function, we have

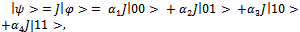(3)

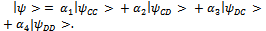Definition 10 We will denominate entangled state basis to the system composed by the following vector states

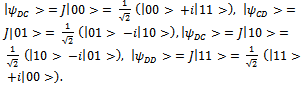Definition 11 We will define as initial state basis to the system composed by vector states |00>, |01>, |10>, |11>.

Definition 12 According to evolutionist game theory, we can present a general game that includes prisoner’s dilemma and attrition in a consistent way

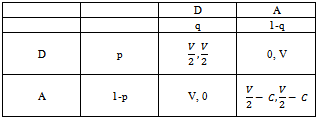Figure 3. Bimatrix game of prisoner’s dilemma and attrition strategies.

Theorem 13 Entanglement operator applied to a symmetrical game, never reduces cooperation probability value p.

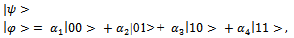(5)

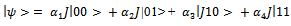(6)

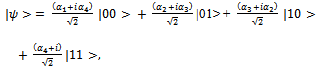(7)

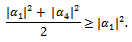(8)

4. Results

Remark 14 Applying the previous theorem to Prisoner’s Dilemma game, we can observe that entanglement always increases cooperation probability from an initial value p = 0 until a final value 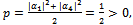While equilibrium in pure strategy (p = 0, q = 0) eliminates cooperation and privileges competition.

Remark 15 In attrition game, initial cooperation probability 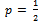remains invariant, after to apply entanglement operator.

In a general way, after applying evolution operator to the function 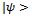we obtain 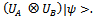Let us take in consideration that the operator UA acts on player A while the operator UB on player B. Let us notice that for a particular case, evolution operators can be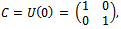

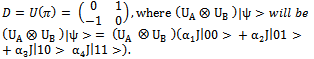(9)

Using equation (9), density operator in entangled state basis is

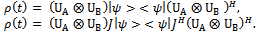(10)

In a similar way, density operator in initial state basis has the next form:

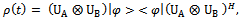(11)

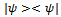Remark 16 Let us remember that density operators and 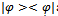are related by a unitary transformation J, such that 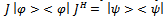then matrices 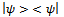and 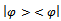has the same eigenvalues and the same characteristic equation; Ben Noble, (1969, pag 312). It is evident that the transformation 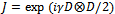is unitary because, it is easy to verify that.

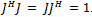Using the previous remark, we can carry out all our analyses in function of initial vectorial basis, because with entangled state basis the results are the same. It is interesting to notice, that, if we take as starting point no-entangled players, evolution operator is given by 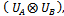and the initial state basis by |00>, |01>, |10>, |11>, while if we take as starting point entangled players, evolution operator is 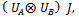and the respective entangled state basis

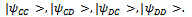Definition 17 The expected utility 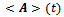of an operator A gives same results with entangled or initial state basis, where A represent utility function, equation (4).

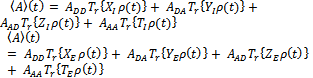(12)

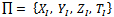The set of Krauss operators is which are defined by 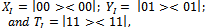in the initial state basis (non-entanglement). Moreover, Krauss operators in entangled state basis are defined by 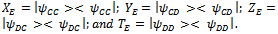The symbol 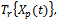means matrix trace of.

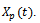Example 18 Let 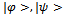state functions of an equiprobable symmetrical game

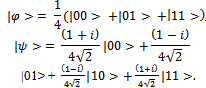(13)

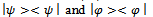We can verify that matrices² has the same characteristic equation 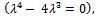and thus, the same eigenvalues. Also, it is important to note that expected utility is the same for entangled and initial state basis. Moreover, we can see the equivalences among partial traces of density operators 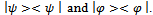For calculation easiness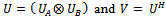. Meanwhile, using projectors 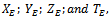the partial traces of density operators 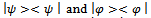are: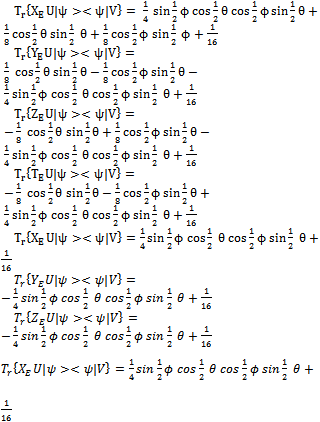

In summary, we verify, that, using the projectors 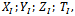the partial traces of the density operators 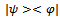are equivalent as follows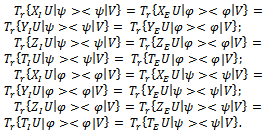

5. Conclusions

1. Life is success of fundamental objectives, which are present in nature and in society as selforganized and recurrent forces of competition, cooperation and coopetition. Pure competition generates winners and losers, pure cooperation generates organized systems, and coopetition gives origin to self-organized and intelligent systems. Fundamentally, self-organized systems indicate existence of two main properties: reversion and evolution. The

first one is related with reversible processes, and it is represented by biconditional |x(t)> → |x(0)> and |x(0)> → |x(t)>, while the second is related with quantum evolution operator, Ut; where |x(t)> = Ut |x(0)>.

2.We have demonstrated that cancer treatment is a quantum game, where are present several features of different nature for instance cooperative, competitive and coopetitive actions. When a cancer treatment controls a game, then common actions are internal cooperation to try to destroy cancer cells, and external competition to avoid to lose healthy cells. If a cancer treatment doesn’t have cooperation as main purpose, then to achieve the biggest objective, to destroy cancer cells, it is unlikely.

3. It is completely innovative to represent a cancer treatment game using instrumental of Game Theory and Quantum Computing. Likewise, it is important introduction of new elements such us internal cooperation and external competition. Said otherwise, it is the coexistence of cooperative and non-cooperative games.

4. Cancer treatment is a phenomenon of cooperation, where entanglement is alone a requirement to cooperation, in that Hameroff has a mistake, because he establishes entanglement as a requirement necessary and sufficient for cancer treatment. While from our viewpoint, entanglement is only a necessary requirement. For us, total cooperation indicates healthy cells, as long as no-cooperation indicates sick cells. That is to say, in biological systems (complex systems), entanglement is a tool controlled by cooperation which increase survival healthy cells.

5. It is important to notice, that interactions between healthy cells are represented by prisoner’s dilemma bimatrix game, while interactions between opponents are represented by attrition game. This reasoning is valid, because, attrition utilities can have negative values, something completely appropriate with reality, because in certain occasions as a result of interaction between two opponents take place serious physical lesions that includes dead. In interaction between partners, modeling as prisoner’s dilemma, strategic interaction is manifested as cooperate or not, without arriving to aggression degree, which is manifested explicitly in interactions between opponents (attrion game), for instance cancer cells.

6. The main theorem of this paper show that entanglement operator applied to a symmetrical game, never reduces cooperation probability value p.

Notes

¹