1. Introduction

Synchronicity is the experience of two or more events that are seemingly causally unrelated, and unlikely to occur together by chance, but that are observed to occur together in a meaningful manner (Jung, 1952). In order to understand synchronicity, theories and technologies have been proposed with insights from sciences, such as biology, physics, psychology, and mathematics (Atmanspacher, 2012; Cambray, 2009; Hogenson, 2014; Peat, 1987; Mansfield, 1995; Sacco, 2018; Sheldrake, 1987). Synchronicity is, therefore, an intrinsically interdisciplinary field. A recent quantitative approach to characterizing synchronicity dynamics was presented in a paper by Sacco (2018). In this paper, Sacco developed the harmonic model (HM) algorithm, which provided a mechanism for quantifying the spatio-temporal dynamics of synchronicity based on the nonlinear and exponential growth properties of the Fibonacci sequence. Confirmation of the ability of HM to predict a higher frequency of synchronicity experience compared to chance comes from a recent study, which demonstrated Jungian analyst synchronicity experiences occurred above chance rates within ±34 days of Fibonacci time patterns (Sacco, 2019a).

The interpretation of the Fibonacci sequence as a bridge between mind and matter correspondences in synchronicity dates back to the seminal work of Jung (Jung, 1976). His primary interest was to understand how the personal and collective unconscious are related in terms of archetypal patterns. Jung identified numbers as the archetypes of order and, as such, ventured to suggest that there must be a connection between synchronicity and the properties of numbers (Jung, 1957). In her study of number and time, Marie-Louise von Franz (Jung’s closest colleague and collaborator) also came to conclude that number can unify mind and matter or psychology and physics (Von Franz, 1974). The world of matter and the world of mind are “bridged” (in Jung’s words) by the Fibonacci numbers: “…synchronicity… is a secondary effect of the primary coincidence of mental and physical events (as in the Fibonacci series). The bridge seems to be formed by the numbers” (Jung, 1976, p. 288).

This paper aims to provide an overview of the approach of dynamical and statistical modeling of synchronicity based on fractal space-time quantum coherency grounded in the golden ratio. First, developments in the nonlinear dynamical modeling and prediction of synchronicity dynamics are described. Subsequently, the statistical characteristics of its resonance boundaries are examined. This is relevant to uncovering the degree of phase-locking, or synchrony, between rhythmic activities of the brain and environment. Such phase locking is shown to be essential for detecting the presence or absence of synchronicity. Finally, attention is given to clinical implications.

2. Nonlinear Dynamics of Synchronicity

Jungian psychology emphasizes notions such as archetypal pattern, teleology, wholeness, integration, number, and time. Undergirding these ideas is nonlinear dynamic systems (NDS), which explores the emergence of ever more complex networks forming spontaneously through self-organization. This way of thinking moves beyond simply causal models and necessarily into the realm of multiplicity, so well described through Jung’s theories of complexes and archetypes. In retrospect, it is clear that from the work of Jung and Von Franz, Jungian psychology anticipated the approach of NDS, and was making the kind of observations necessary to build a scientific theory about synchronicity experience. Nevertheless, researchers from the Jungian psychology tradition were hindered by a lack of methodology sufficient for measuring complex change over time.

Over the past 20 years, however, there has been increasing use of NDS in psychology (Guastello, Koopmans, & Pincus, 2008). NDS is a general systems theory for describing, modeling, and predicting change processes. NDS may be defined by looking at each term separately. Nonlinear means that causal connections are potentially disproportionate: Small changes in one variable may lead to large changes in another and so on. Dynamical refers to change over time. Systems refer to the focus on interactions of multiple components that are combined into an integrated whole. On a methodological level, the primary difference between NDS and the general linear model is the ability of NDS models to account for empirical phenomena that do not produce normal frequency distributions.

The current paper is focused on a particular class of non-normal and nonlinear processes, self-organization, as it applies to the emergence of relationships among brain and environment. Self-organization is a process that occurs in systems, whereby the exchange of information (or matter and energy in physical systems) among agents at a particular scale (i.e., magnitude) leads to the emergence of global order at a higher scale, allowing for complex regulatory feedback mechanisms back down to the level of the agents (Bak, 1996; Thelen & Smith, 1994). This type of model may be particularly useful in explaining why synchronicity tends to be associated with interconnectedness, and how this interconnectedness spreads circularly from the individual level to the global level and back to the individual level.

One key characteristic of self-organizing systems is that their outputs often follow a frequency distribution known as an inverse power law (Guastello et al., 2008). In other words, these systems display many small change events and exponentially fewer large change events over time. A related feature of self-organizing systems is that they have fractal properties (Bak, 1996). Fractals are defined by three overlapping characteristics. First, fractals are scale-free, meaning that in an idealized (i.e., mathematical) sense, they are infinitely detailed. As such, models of synchronicity may involve a combination of clear-cut structure (e.g., mind-mind, mind-object correspondence) and also large degrees of complexity and unpredictability. The second characteristic of fractals is referred to as self-similarity, which means that self-organizing systems contain similar processes and structures across different scales. Within synchronicity, this may help explain how tiny symbols can have drastic effects. Moment-to-moment fluctuations within cognition should be self-similar to longer scale dynamics, week-to-week, month-to-month, and year-to-year. A ubiquitous physical example of self-similarity may be found in branching patterns such as trees with branches of an ever-decreasing size that mirror the shape of the tree as a whole. The third characteristic of fractals is that they do not have a whole number dimension. Although a point exists in only one dimension, lines exist in exactly two dimensions, and cubes in three dimensions; fractals exist in dimensions that are fractions. This is because their infinite detail defies absolute measurement, at least in a mathematical sense. The golden ratio is an irrational number that can be approximated by continued fractions. Furthermore, the relationship between the golden ratio and continued fractions is that the convergents of the continued fraction are the ratios of consecutive Fibonacci numbers.

A recent study tested whether two models based on the Fibonacci numbers significantly predicted synchronicity experience compared to expected distributions based on chance (Sacco, 2019a). It was found that predicted dates from a fractal harmonic model provided a significantly better fit to the observed data compared to chance, yielding a significance level of .096 and medium effect size. This suggests that synchronicity experience could be modeled as self-organizing, with global order emerging cyclically and automatically once the developmental process becomes activated at birth. Furthermore, the fractal organization of the harmonic model suggests that, like other self-organizing systems in nature, synchronicity has the three characteristics of fractals listed above. To model and predict synchronicity dynamics, we first need to understand the origin of fractal dynamics. How do they form? The following section provides a much-needed discussion on this fundamental, but seriously ignored question.

2.1. Modeling and Prediction of Synchronicity Dynamics

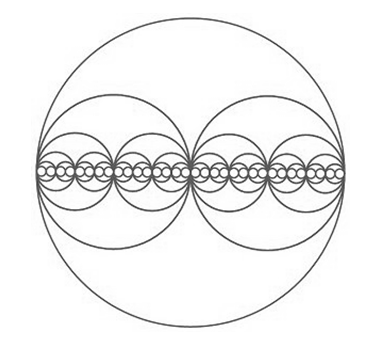
If we are to understand the origin of fractals, we first need to understand the nature of motion. For instance, consider the sine wave. The sine curve is very important in both mathematics and physics because of its central role in harmonic analysis and the universality of oscillation in nature. The sine curve is everywhere in nature, from subatomic vibrations to planetary motion, solar cycles, and galactic rotations. Oscillation is the most energetically efficient kind of movement.

For this reason, oscillatory processes determine the organization of matter at all levels—from atoms to galaxies. Now, let us repeat the sine wave (see Figure 1). Note how with each additional octave, the sine curve appears with more detail. Also, note the fractal self-similarity in the scale. If you zoom in on the sine curve, a smaller part looks the same as the whole thing, and each section looks more or less the same as any other section. Thus, motion implies fractality.

Figure 1. Fractal doubling of the sine wave. On each iteration, each half of the sine wave is filled with a sine wave of half the diameter. This form is related to many other fractal forms including, in particular, the Cantor dust set

In addition to encompassing fractal self-similarity, the nested sine wave depiction includes important temporal considerations. Consider the period-doubling sequence in the diagram of Fig. 1. With the further increase of iteration, a new periodic orbit with periodicity two emerges, and then periodic orbit of period four and so on. Each subsequent orbit in the period-doubling cascade results in a bifurcation. The notion that the universe represents the operation of this iterative doubling process is a common theme in cosmological theory (Shu, 2019). In cosmology, the Big Bang expansion of space is assumed to have occurred spontaneously, resulting in a period of geometric doubling some 50 to 100 times, and possibly many more. Inflationary expansion is the mechanism for setting a direction to time’s arrow. The universe during inflation doubled in size about every 10^-37 seconds, while the doubling time today is roughly 14 billion years. Remarkably, the Fibonacci numbers and golden ratio arise spontaneously from the doubling sequence (Linage, Montoya, Sarmiento, Showalter, & Parmananda, 2006). Ultimately, then, the simplest iterative dynamical system is constructed from the doubling sequence and Fibonacci numbers.

The Fibonacci Life Chart Method (FLCM) (see Sacco, 2013) is a methodology that models the cognitive development process by using the Fibonacci numbers as an epigenetic timing mechanism. The general idea is that cognitive development should be characterized as a continual coupling among brain, body, and environment that unfolds in discrete time steps of Fibonacci time intervals. Development and growth is a fractal hierarchy of self-similar cycles at multiple levels (e.g., atoms, molecules, genes, cell, organ, organism, behavior, and environment) and organized by the characteristic spacetimes of the processes involved. All real processes have characteristic space time scales. There are 24 orders of magnitude in scale from the smallest known particle the neutrino (~1 ym) to our human scale (~ 1m). Time intervals also span several orders of magnitude. Electrons move in 10^-12 seconds, nerve cells fire in a tenth of a second or faster, the heart beats in a second, the embryo doubles every 24 hours, and physiological processes have longer cycles of a month or year. The coherent fractal hierarchy of living activities arises because processes with matching space times interact most strongly through resonance, and also link up to the entire hierarchy. That is why biological activities come predominantly in cycles or biological rhythms.

Within a fractal scaling model of quantum harmonic oscillators, it was shown that scaling is a fundamental property of any natural oscillation process (Müller, 2009). In living systems, fractals must satisfy the state of quantum coherence, which maximizes global cohesion as well as local autonomy and enables energy from any local level to spread to the global and conversely concentrate energy to any domain from the entire system. Fractals with fractal dimension in the golden ratio might be the most effective in giving autonomy to the greatest number of cycles because of the golden ratio’s link to the fine-structure constant (Miller, 2010; Sherbon, 2018). Global cohesion is also ensured because cycles in a fractal hierarchy are quantum coherent; energy can be shared between global and local. The golden ratio is also close to an infinite number of rational ratios based on the Fibonacci numbers, so special resonances or correlations can be easily established (Livio, 2008). Thus, one would expect biological rhythms, in general, to conform to the golden ratio, and indeed this appears to be the case. For example, body temperature is a classic phase marker for measuring the circadian rhythm and is at a minimum during sleep at around 04:00 hours and begins to increase before wakefulness until a maximum is reached at around 18:00 (Minors & Waterhouse, 1981). The hours 04:00 and 19:00, on a 24-hour clock, are at an angle of 137.5° (the golden angle). In short, body temperature tends to fluctuate within the range of the golden ratio, with exogenous sources of variability such as sleep and exercise (Hiddinga & Van Den Hoofdakker, 1997).

The golden ratio also figures prominently in the EEG frequencies of the resting brain (Pletzer, Kerschbaum, & Klimesch, 2010). Oscillatory activity in the brain is observed at different levels of organization and is thought to play a vital role in cognition. To link subjective experience to the body, also known as the mind-body problem (Chalmers, 1995), it must be acknowledged that cognition is dramatically rhythmic (Buzsáki, Logothetis, & Singer, 2013; Thaut, et al. 2005). Thought patterns take on rhythmic periods. As one ponders what to do with the day, there is a cyclical nature to this musing. When solving a difficult problem, the idea is mentally replayed many times. Each time the problem is replayed, there is a new chance to connect the thought to new solutions. Music also taps into the nature of humanity because of its rhythmic nature. Unfortunately, there has been no theory that explains how the large-scale organization of the human brain can be related to our environment. This is astonishing because neuroscientists generally assume that the brain represents events in our environment by decoding sensory input. It is proposed that the brain models the environment as a collection of hierarchical, dynamical systems, where slower changes provide the context for faster changes (Kiebel, Daunizeau, & Friston, 2008). This provides a framework for integrating the quantum scale to the everyday scale by a single mathematical principle. Such a model yields iterative long-term predictions that can be used for synchronicity forecasting.

2.2. Spatio-Temporal Dynamics

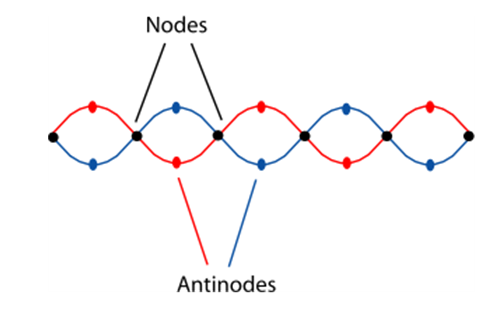
According to the Fibonacci Life Chart Method (FLCM) (see Sacco, 2016, 2018), the spatio-temporal structure of synchronicity dynamics is explained by the Fibonacci numbers and golden ratio. The time-series data from the FLCM were first used to represent synchronicity dynamics based on the golden ratio of internal and external division (Sacco, 2016). However, it was not found in empirical study to capture the actual dynamics of synchronicity, in part because fractals can only pass information in one direction (upwards) and cannot be extrapolated backward (irreversibility) to determine the rules/laws that govern them (Gardiner, 2013). In an important advance, Sacco (2018) showed that the concept of resonance can be used to extend FLCM time series data forward in time. Standing-wave resonance implies both nodes (regions of maximum vibration) and antinodes (regions of minimum vibration) spaced at equal wavelength intervals (Figure 2). Thus, based on the FLCM, the harmonic model describes the overall node spacing along the standing wave harmonics in terms of the Fibonacci periods of 1.67, 2.70, 4.37, 7.08, 11.45, 18.53, 29.99, 48.52, and 78.51 years. Each attribute in the standing wave resonance pattern should have some importance to the prediction of synchronicity (see Sacco, 2018).

Figure 2. A standing wave pattern has nodes and antinodes—two extreme positions of the resonance pattern. The harmonic model time series is an iterative map computed using iteration from one time point to the next, applying the same resonance dynamic, and selecting only the peak events (nodes and antinodes) of the system, thus offering a condensed (and “strobe-like”) picture of long-term behavior

An essential feature of the harmonic model is the first-order harmonic, which is 1.67 years. A first-order harmonic is one that does not have any other harmonics riding upon it; it is, therefore, a higher frequency wave. This is modeled as the interval of 1.67 years because there is no significant higher cortical function and, subsequently, no strong evidence of well-integrated cognitive functioning before this age. Furthermore, brain scans qualitatively begin to resemble the adult brain only after one to two years (Knickmeyer et al., 2008). What that means is that initially, before conscious awareness, the processing is primarily modular, with numerous simultaneous activations happening in parallel. However, at the time when we begin to see conscious awareness emerge, studies show a synchronization of many areas that start to work together (Yanagawa, Chao, Hasegawa, & Fujii, 2013). Thus, the difference between conscious and unconscious states is the degree of neural integration, with the sense of self-identity modeled as emerging at age 1.67.

The key feature of the spatio-temporal modeling is the cyclic time series data so that elements of the state space will be repeated periodically in the time series. Cycles are intimately tied to the study of dynamical systems, beginning with celestial mechanics. Newton tried to describe the planetary cycles in terms of his laws of motion more than 300 years ago. Indeed, the present methodological strategy has a strong correlation with planetary motion based on entrainment to the golden ratio (Sacco, 2019b). This new model can help facilitate a better understanding of techniques traditionally used in predictive astrology, and can, therefore, improve understanding of the prediction of synchronistic events based on the positions of planetary motion (Jung, 1952). However, predictive astrology has several shortcomings in terms of predictability, such as lack of scientific theory, not linking orbital periods to fixed mathematical laws, and the potential for under specification of the model. From the scientific perspective of dynamic systems theory, the activities of astrology take on a profoundly different meaning than that ordinarily attributed to them.

The tradition of astrology shares a history of misrepresentation and misunderstanding. In contemporary culture, it exists as a crude and largely faddish mechanism for predicting life events. And yet, as Jung reminds us “astrology was the first form of psychology” (Rossi & Le Grice, 2017, p. 23) and represents the “sum of all the psychological knowledge of antiquity” (Rossi & Le Grice, 2017, p. 23). Jung found in astrology a source of spiritual and psychological meaning and suggested: “Astrology would be an example of synchronicity on a grand scale if only there were enough thoroughly tested findings to support it” (Rossi & Le Grice, 2017, p. 177). The tradition of astrology represented the connectivity between the macrocosm and microcosm, between two apparently different realms, which are actually one unit, based on mathematics. It was this relationship among all elements of the human and physical world that the ancients knew and experienced. Thus, astrology was a particular expression of a world view that was holistically patterned, alive, and spiritual. The connection between the harmonic model and astrology provides a way in which modern and ancient knowledge could be linked.

3. Statistical Characteristics

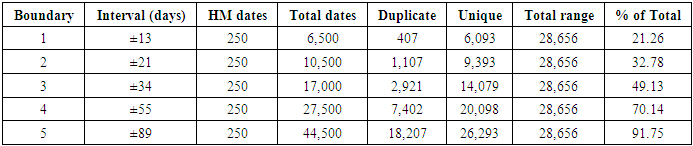
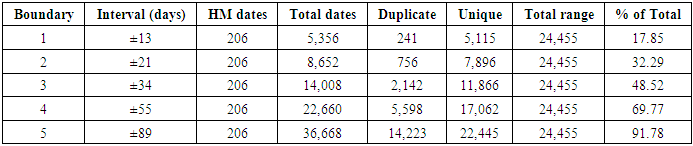
One way the phenomenon of synchronicity can be identified and validated is by statistical distributions of time scales. The fractal properties of the frequency distribution are one of the telling indicators of synchronicity. By observing a single synchronistic event, it would be impossible to establish whether the synchronicity is in a self-organized state or not. Statistics is, therefore, of principal importance for modeling and interpretation of synchronicity phenomena. Of course, only for strictly deterministic systems can one precisely predict the outcome of an event based on its initial conditions. However, in reality, initial conditions are never known precisely, and many random disturbances occur during the progression of an event, which prevents us from making precise predictions. The most precise statement we can make about almost any physical system is of statistical nature.

The first step in the statistical modeling of synchronicity is to determine the base rate of chance patterns within the HM time series. In determining this base rate for chance pattern analysis in the HM, one must consider resonance boundary conditions. In a time series, an event can be defined by a start time, a peak time, and an end time, which yields a useful definition for the duration of an event. However, there is no obvious way of measuring resonance boundary conditions from the HM time series. Thus, the idea is to induce a probability distribution on the dates of the time series so that the duration criterion is satisfied. When a synchronistic event is within the resonance boundary of the time series, a so-called “probabilistic resonance” occurs. This type of probabilistic resonance is central to the proposed implementation of the statistical analysis and determination of the base rate of chance patterns.

The way to define various probabilistic resonances has been to define general upper and lower boundaries of the resonance distribution based on Fibonacci numbers (Sacco, 2019a). The output of the resulting event statistics, in the form of expected distributions and correlations, can then be cross-compared with those of observed distributions of synchronistic events. Table 1 shows the expected distribution of the time series based on five Fibonacci number boundaries from ±13 to ±89 days. For each Fibonacci number boundary, there is a regime that corresponds to oscillation around the nodes and antinodes of the time-series where synchronistic effects could be predicted, which is called the synchronization range. Each Fibonacci boundary can be placed within one of three categories: (i) synchronistic; (ii) quasi-synchronistic; or (iii) outside the synchronization regimes.

Table 1. Analysis of Fibonacci Harmonic Model Time-Series

As can be seen in Table 1, the different Fibonacci number boundaries result in different resonance boundary distributions. For example, for the lower boundary of Fibonacci numbers (±13 days), there are 6,500 harmonic dates, but approximately 6% of the dates (407) are duplicate dates in the time series. Omitting the duplicate dates, the total number of unique dates for the ±13 days interval is 6,093. The percent of this boundary condition to the overall average lifespan of 78.51 years (28,656 days) is 21.26%. If observed synchronistic events are indistinguishable from random chance, the frequency of observed synchronistic events should not depart significantly from this baseline chance rate over the events in the data set. Across the synchronization range, synchronicity has been found to occur above chance rates only at the ±34 days boundary (Sacco, 2019a). If a sufficient lock-in range is not available, then the brain-environment system must go out of synchronization. For the ±55-day and ±89-day categories, the regime is deemed “outside” the synchronization range. Outside the synchronization range, the regime shift becomes indistinguishable from random events.

Table 2. Analysis of Fibonacci Harmonic Model Time-Series after age 11.5

The resonance boundary conditions just described approached all harmonic dates in the lifespan from birth to average life expectancy. However, these should be considered as merely calculated values. The determination of resonance distribution boundaries for synchronicity is complicated by the complex processes which are involved in the appraisal and interpretation of synchronicity experience. Cognitive development means growth in the ability to think and reason. Under Piaget’s theory of cognitive development, the fourth and final stage of development is the formal operational stage (Piaget, 1964). This stage typically begins around age 11 years, where children attain complex thinking skills. Given the nature of cognitive development, the resonance boundary conditions can be reanalyzed to take into account indicators of cognitive development. The scenario with cognitive development after age 11.5 years was calculated and shown in Table 2. As can be seen in Table 2, the statistics of boundary conditions do not change considerably in the case of expected correlations based on indicators of cognitive development. An even more practical method is to calculate the boundary conditions based on the age range of observed synchronicity events in a given data set. This is expected to yield a more precise characterization of statistical properties and is thus better suited in the study of synchronistic phenomena (see Sacco, 2019a).

3.1. Remarks on the Boundaries

As a relatively new methodology for analyzing synchronicity dynamics, it is worthwhile to briefly explain some of the most important methodological considerations of the harmonic model. Foremost, it is crucial to keep in sight the essential quantitative and qualitative dependency relationships. The quantitative dependency structure is defined by associating with each calendar date a conditional resonance probability distribution. Considering the qualitative dependency structure of the HM, given a set of calendar dates, it is essential to consider individual differences in the coding of synchronistic patterns (e.g., patterns involving two or more events that are causally unrelated occurring together in a meaningful manner), and the potential for spurious impacts of miscoded patterns. Within a recent study (Sacco, 2019a), the relevant time for detecting phase locking of synchronicity experience was ±34 days. The data appeared sufficiently reliable as well to support the qualitative dependency analyses, based on the education levels and years of experience of the Jungian analysts. Future research will also need to carefully examine the reliability of any data used because moderate or low levels of reliability will be likely to obscure the qualitative structural properties of the model. This would be particularly problematic in comparisons across studies with different degrees of reliability in the data.

An additional consideration of the current methodology is the use of chi-square statistics to compare the observed distribution of cases against an expected one. The chi-square test can only be applied to data classified into categories. Most statisticians warn against using the test when any of the expected values are less than 5. None of the expected values were less than 5 in the above-described study (i.e., Sacco, 2019a), so the assumptions for the chi-squared test were reasonably satisfied. Chi-square test tells us whether the classifications on a given population are dependent on each other or not. However, the establishment of statistical association by means of chi-square does not necessarily imply any causal relationship between the attributes being compared, but it does indicate that the reason for the association is worth investigating. The p-value of .05 has been the standard permissible level of chance observation in most models assessing causation. Yet, the position of the p-value in statistical analyses has been challenged by statisticians and other scientists (Bakan, 1966; Berkson, 1942; Cohen, 1994; Cumming, 2014). It would be a mistake to dismiss any empirical finding that is based on a distribution with a p-value above .05. Cumming (2008) compellingly argues that the p-value should be combined with information about effect sizes. An interpretation based on effect size suggests that Fibonacci time series might be predictive of synchronicity experience (Sacco, 2019a), although more research is needed.

Finally, at the level of discussion, the harmonic model tries to understand the connection between two phenomena in physics, classical chaos and quantum mechanics. Although both theories highlight the unpredictability of nature, they are very different theories that mix uneasily. The main reason is the fact that chaos theory is deterministic while quantum theory is probabilistic. Another reason is the non-linearity of chaos theory versus the linearity of probability waves employed in quantum theory. A third reason is the need for certainty about parameters in chaos theory versus the Heisenberg uncertainties of competing measurements (such as momentum vs. location) in quantum theory. Yet, despite such fundamental differences, there are attempts underway to combine those two theories in what is called “quantum chaos.” For example, periodic orbit theory (Cvitanovi´c & Eckhardt, 1989) makes connections between the periodic orbits of a classical system and quantum resonances, which may have relevance to the mechanisms of the Fibonacci harmonic model.

4. Clinical Implications

Although preliminary, the results of the current study help to validate several aspects of clinical wisdom from clinical practice. First, it appears that synchronicity experience may significantly affect psychotherapy outcomes (Beitman, Celebi, & Coleman, 2009; Roxburgh, Ridgway, & Roe, 2016). By extension, more intense experiences of synchronicity may have an even greater impact. Second, the periodic fractal structure observed within synchronicity dynamics may provide a deeper justification for the clinical focus on cycles, since cycles appear to play a central role in psychodynamics (Wachtel, 2017). Cycles may be identified through rigidity (i.e., repetition) in the behavioral output of a system (i.e., patterned interactive behaviors) over time. The experience of going round and round during the life course appears to be literal. Third, clinicians may wish to consider the potential spiritual function that may be served by synchronicity experiences (Main 2007), aiming at understanding and increasing flexibility in their clients. Synchronicity counseling should be facilitated with care so as not to inadvertently increase the rigidity of the system, or push the system beyond its limits toward a state of disintegration. Approaches that emphasize high levels of empathy and a focus on process rather than the specific content of sessions may be seen as particularly well suited (Cho, Miller, Hrastar, Sutton, & Younes, 2009). Finally, clinicians may gain a deeper perspective on synchronicity, not as an abnormal trait or state, but rather as a critical process in the growth of individuals and their relationships.

On a grander scale, the current study provides some grounding to the common-sense notion that human beings are meaning-seeking creatures (Frankl, 1985; James, 1902; Jung, 1933). Meaning may be considered to be a natural, emergent outgrowth of information exchange among individuals: a self-organizing, self-regulating information-nest, emerging and evolving from the combined flows of information within individuals and feeding back to either spur or hinder self and social evolution. More simply, both the self and communities may be considered to be information processors. At each level, coherence and complexity seek balance to assimilate and accommodate the flows of information from a coherent yet complex world. Various clinical approaches to meaning and spirituality may be integrated through the potential structural significance of synchronicity as a process of global order formation, whereas synchronicity integration may be considered to be the primary route to growth for individuals, as well as communities.

5. Conclusions

The human brain is an archetypical complex system, and the modeling of this system using new approaches has provided a framework for the scientific study of synchronicity. This is achieved using two complementary approaches, which emphasize the dynamical and statistical features. The dynamical approach is based on the Fibonacci sequence and forward simulations of brain-environment interaction loops, generated by computer modeling. Many factors, such as the boundary conditions, the dynamical mechanisms, and the neural network architecture as well, are important for the refinement of the model. The statistical approach emphasizes the correlations among the different resonance boundary conditions using chi-square statistics (Sacco, 2019a). The characteristic features obtained are summarized as follows: The resonance boundary conditions give limited predictability of synchronicity experience of between ±34 days, and its predictability is probabilistically determined via Fibonacci harmonic resonances.

The emphasis of this approach is on how the brain/body/environment system as a whole change in real time to predict instances of synchronicity (i.e., an overlapping in meaning between physical and psychological phenomenon). Dynamics based on Fibonacci harmonic resonance is proposed as the best framework for capturing that change. The harmonic model approach allows for statistical analysis of synchronicity based on processes through a dynamical system. This can be regarded as an important breakthrough because, in the past, there were very few links between dynamical and statistical modeling (Main, 2018). Most dynamical models of synchronicity did not quantify the time-series (Atmanspacher & Fach, 2019), while most statistical models did not mirror the real mechanisms involved (Storm & Rock, 2014). The main idea of the harmonic model approach is to divide a complex process (e.g., synchronicity experience) into a hierarchy of submodels or levels, conditional on one another. In such a model, statistical resonance appearing at different levels are assumed to be interdependent (Sacco, 2018). This way, synchronicity can be specified by resonance boundary conditions reflecting all possible interdependencies between the model components and parameters. The maturing of these methods and techniques can lead to a better understanding of the dynamical processes essential from both a basic science and clinical intervention perspective.