-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Agriculture and Forestry
p-ISSN: 2165-882X e-ISSN: 2165-8846
2012; 2(5): 235-238
doi: 10.5923/j.ijaf.20120205.06
Mass Modeling of Castor Seed (Ricinus Communis) with Some Geometrical Attributes
Ali Nejat Lorestani , Akbar Kazemi
Mechanical Engineering of Agricultural Machinery Department, Razi University, Kermanshah, 6715685438, Iran
Correspondence to: Ali Nejat Lorestani , Mechanical Engineering of Agricultural Machinery Department, Razi University, Kermanshah, 6715685438, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Horticultural crops with the similar weight and uniform shape are in high demand in terms of marketing value. Therefore, an awareness of grading fruits and vegetables based on weight is crucial. A part of this research was aimed to present some physical properties of Castor seed. In addition, in this study the mass of Castor seed variety was predicted with using different physical characteristics in four models includes: Linear, Quadratic, S-curve, and Power. According to the results, all properties considered in the current study were found to be statistically significant at the 1% probability level and the best and the worst models for prediction the mass of Castor seed were based on third projected area and first projected area of the Castor seed with determination coefficients of 0.82 and 0.757, respectively. At last, mass model based on third projected area from economical standpoint is recommended.
Keywords: Mass, modeling, Castor seed, physical characteristics
Article Outline
1. Introduction
- Ricinus communis seed, commonly known as “higuerilla”, “ricine” or “mamona”, is a member of the Euphorbiaceae family and it is native from tropical climates although it has been adapted to a wide range of sub-tropical and temperate climates. The R. communis plant has been cultivated since antiquity not only as a garden ornament for its striking foliage and interesting flowers but also because their seeds were used as a medicinal plant. The annual world production is around one million tons and nowadays it is used mainly for the production of non-edible oil, as these seeds are poisonous to humans and animals, because they contain ricin, a protein with cytotoxic activity that inhibits protein synthesis at ribosome levels[1]. R. communis plant is considered as an important source of oil because of their seeds which contain about 35–55% of oil by weight. The oil, also known as “castor oil”, enjoys a tremendous annual demand worldwide, which is estimated in about 220,000 tons[1]. It contains a high concentration (over 85–90%) of ricinoleic acid (12- hydroxy-oleate), which has multiple nonfood applications in the production of different products such as paints and varnishes, nylon-type synthetic polymers, fungicides, medications, cosmetics, hydraulic fluids and high quality lubricants. As additive, the ricinoleic acid has been found useful to replace sulfur based lubricity components in petroleum diesel, helping to reduce sulfur emissions, among others Applications[1].To design and optimization a machine for handling, cleaning, conveying and storing, the physical attributes and their relationships must be known. As an instance, grading of fruits by their size can be replaced with grading by their weight because it may be more economical. Grading fruit based on weight is important in packing and handling. In nearly all cases raw product grades are based on weight[2]. Size and shape determine how many fruit can be placed in containers of a given size. Volume and surface area could be beneficial in proper prediction drying rates and hence drying time in the dryer. On the other hand, volume and its relationship with packing coefficient are very important because having any information about Packing coefficient of fruits could result in efficient control of fruit quality during storage. Physical characteristics of agricultural products are the most important parameters to determine the proper standards of design of grading, conveying, processing and packaging systems[3].Among these physical characteristics, mass, volume, projected area are the most important ones in determining sizing systems[4, 5]. Many researches have been conducted to find physical properties of various types of agricultural products. Mass grading of fruit can reduce packaging and transportation costs, and also may provide an optimum packaging configuration[6]. Determining relationships between mass and dimensions and projected areas may be useful and applicable[7, 8]. Tabatabaeefar predicted apple mass by models that were based upon apple physical properties[3]. Al-Maiman studied the physical properties of pomegranate and found models of predicting fruit mass while employing dimensions, volume and surface areas[9]. Keramat investigated some physical properties of date (cv. Lasht). They determined dimensions and projected areas by using image processing technique[10]. Lorestani concluded that the linear regression models of kiwi fruit have higher R2 than nonlinear models for them, and are economical models for application. Among the linear regression dimensions models, the model that is based on width and among the linear projected area models, the model that is based on third projected area, and among the other models, the model that is based on measured volume, had higher R2, that are recommended for sizing of kiwi fruit[11]. Also Tabatabaeefar determined a total of 11 regression models in the three different categories for two different varieties of apple fruits[3]. Lorestani concluded that the best model for prediction the mass of Fava bean among the dimensional models was Linear as:
 and the best model for prediction the mass of Fava bean was based on third projected area which perpendicular to L direction of Fava bean and it was Power form as
and the best model for prediction the mass of Fava bean was based on third projected area which perpendicular to L direction of Fava bean and it was Power form as 
 and the worst was based on first projected area of Fava bean and it was Linear form as
and the worst was based on first projected area of Fava bean and it was Linear form as 
 [12].No detailed studies concerning mass modeling of Castor seed (Ricinus Communis) have yet been performed. The aims of this study were to determine the most suitable model for predicting Castor seed mass by its physical attributes and study some physical properties of Iranian Castor seed to form an important database for other investigators.
[12].No detailed studies concerning mass modeling of Castor seed (Ricinus Communis) have yet been performed. The aims of this study were to determine the most suitable model for predicting Castor seed mass by its physical attributes and study some physical properties of Iranian Castor seed to form an important database for other investigators.2. Materials and Methods
- The common Castor seed was obtained from farms located in the west of Iran in June2011. 100 Castor seed samples collected from cultivations growing in Iranian farms were used for measurement in the Biophysical laboratory and Biological laboratory of Razi University of Kermanshah, Iran. The samples were weighted and dried in an oven at 105℃ for 24 h[13] and then weight loss on drying to final content weight was recorded as moisture content. The remaining material was kept in the desiccators until use. Castor seed mass (M) was determined with an electronic balance with 0.01 g sensitivity. To determine the average size of the samples, three linear dimensions namely as length, width and thickness were measured by using a digital caliper with 0.01 mm sensitivity. Volume (V) was determined by the water displacement method[14]. The geometric mean diameter (Dg) and surface areas (S) were determined by using following formulas[14], respectively:
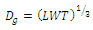 | (1) |
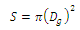 | (2) |
 | (3) |
 | (4) |
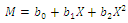 | (5) |
 | (6) |
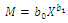 | (7) |
3. Results and Discussion
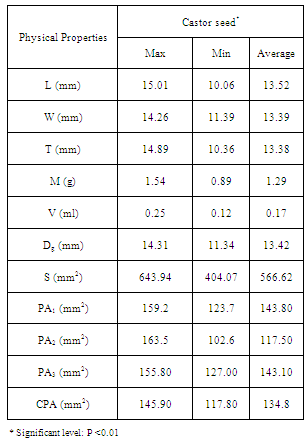
- A summary of the physical properties of Castor seed is shown in Table 1. These properties were found at specific moisture contents about 85.82% wet basis.
|
 Whereas this model can predict the relationships between the mass with thickness and width with R2 of 0.701 and 0.547, respectively.Tabatabaeefar reported that among systems that sort oranges based on one dimension, the system that applies intermediate diameter is suited with nonlinear relationship[16].For prediction of the mass of Castor seed based on volume the best model was Linear with R2 = 0.409.
Whereas this model can predict the relationships between the mass with thickness and width with R2 of 0.701 and 0.547, respectively.Tabatabaeefar reported that among systems that sort oranges based on one dimension, the system that applies intermediate diameter is suited with nonlinear relationship[16].For prediction of the mass of Castor seed based on volume the best model was Linear with R2 = 0.409.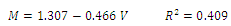 According to the results, for prediction of the mass of the Castor seed based on geometric mean diameter, Quadratic model was the best models with R2 = 0.741.
According to the results, for prediction of the mass of the Castor seed based on geometric mean diameter, Quadratic model was the best models with R2 = 0.741.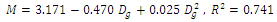 This model is not economical because for calculating the geometric mean diameter(Dg) we must measure three dimensions of Castor seeds and it is time consuming and costly.For mass modeling of Castor seed based on projected areas including PA1, PA2 , PA3 and CPA, the best model was Quadratic with R2 = 0.870.
This model is not economical because for calculating the geometric mean diameter(Dg) we must measure three dimensions of Castor seeds and it is time consuming and costly.For mass modeling of Castor seed based on projected areas including PA1, PA2 , PA3 and CPA, the best model was Quadratic with R2 = 0.870. For prediction of the mass of the Castor seed based on surface area the best model was Quadratic with R2 = 0.742.
For prediction of the mass of the Castor seed based on surface area the best model was Quadratic with R2 = 0.742.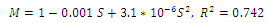 According to the results the Quadratic model could predict the relationships among the mass and some physical properties of Castor seed with proper value for determination coefficient. So we suggest the Quadratic model based on projected area for prediction the mass of Castor seed because we need one camera and it is applicable and economical method.
According to the results the Quadratic model could predict the relationships among the mass and some physical properties of Castor seed with proper value for determination coefficient. So we suggest the Quadratic model based on projected area for prediction the mass of Castor seed because we need one camera and it is applicable and economical method.4. Conclusions
- Some physical properties and their relationships of mass of Castor seed are presented in this study. From this study it can be concluded that:1. All properties considered in the current study were found to be statistically significant at the 1% probability level.2. The best model for prediction the mass of Castor seed among the dimensional models was Quadratic as:

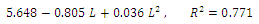 3. The best model for prediction the mass of Castor seed was based on second projected area which perpendicular to W direction of Castor seed and it was Quadratic form as
3. The best model for prediction the mass of Castor seed was based on second projected area which perpendicular to W direction of Castor seed and it was Quadratic form as 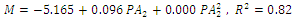 , and the worst was based on first projected area of Castor seed and it was Linear form as
, and the worst was based on first projected area of Castor seed and it was Linear form as 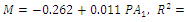
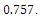 4. At last, mass model based on second projected area from economical standpoint is recommended.This information can be used in the design and development of sizing mechanisms and other post harvest processing machines. At the end, it is recommended that other properties of Castor seed such as thermal, mechanical, and nutritional characteristics are to be studied and changes of these properties are to be examined as a function of moisture content and ripening phases.NomenclatureM= fruit mass, g; V= fruit Volume, cm3; Dg = geometric mean diameter, mm; S= surface area, mm2; L= length of fruits, mm; W= width of fruit, mm; T= thickness of fruit, mm; PA1 = first projected area, mm2; PA2 = second projected area, mm2; PA3 = third projected area, mm2; CPA= criteria projected area, mm2; b0,b1,b2 = curve fitting parameters; X= independent parameter.
4. At last, mass model based on second projected area from economical standpoint is recommended.This information can be used in the design and development of sizing mechanisms and other post harvest processing machines. At the end, it is recommended that other properties of Castor seed such as thermal, mechanical, and nutritional characteristics are to be studied and changes of these properties are to be examined as a function of moisture content and ripening phases.NomenclatureM= fruit mass, g; V= fruit Volume, cm3; Dg = geometric mean diameter, mm; S= surface area, mm2; L= length of fruits, mm; W= width of fruit, mm; T= thickness of fruit, mm; PA1 = first projected area, mm2; PA2 = second projected area, mm2; PA3 = third projected area, mm2; CPA= criteria projected area, mm2; b0,b1,b2 = curve fitting parameters; X= independent parameter.ACKNOWLEDGEMENTS
- The authors would like to express their gratitude and their sincere appreciation to the Deputy of Agronomy Departments for their cooperation and laboratory support at the Razi University of Kermanshah.
References
| [1] | Perea-Flores, M.J., Chanona-Pérez, J.J., Garibay-Febles, V., Calderón-Dominguez, G., Terrés-Rojas, E., Mendoza-Pérez, J.A., & Herrera-Bucio, R. (2011). Microscopy techniques and image analysis for evaluation of some chemical and physical properties and morphological features for seeds of the castor oil plant (Ricinus communis). Industrial Crops and Products. 34, 1057– 1065. |
| [2] | O'Brian, M., & Floyd, S. (1978). A micro computer controlled weighing and print out system for fruit and vegetable grading. Transaction of the ASAE. 16, 446-450. |
| [3] | Tabatabaeefar, A., & Rajabipour, A. (2005). Modeling the mass of apples by geometrical attributes. Scientia Horticulturae, 105, 373-382. |
| [4] | Peleg, K., & Ramraz, Y. (1975). Optimal sizing of citrus fruit. Transaction of the ASAE. 18 (6), 1035–1039. |
| [5] | Khodabandehloo, H. (1999). Physical properties of Iranian export apples. M. Sc. Thesis. Tehran University, Karaj, Iran, pp. 1–102. |
| [6] | Peleg, K. (1985). Produce Handling, Packaging and Distribution. The AVI Publishing Company. Inc. Westport, Connecticut, pp. 20-90. |
| [7] | Stroshine, R. (1998). Physical Properties of Agricultural Materials and Food Products. Course manual. Purdue Univ. USA. |
| [8] | Marvin, J.P., Hyde, G.M., & Cavalieri, R.P. (1987). Modeling potato tuber mass with tuber dimensions. Transactions of the ASAE 30, 1154-1159. |
| [9] | Al-Maiman, S., & Ahmad, D. (2002). Changes in physical and chemical properties during pomegranate (Punica granatum L.) fruit maturation. Journal of Food Chemistry. 76(4), 437-441. |
| [10] | Cárcel, L.M., Bon, J., Acuña, L., Nevares, I., del Álamo, M., & Crespo, R. (2012). Moisture dependence on mechanical properties of pine nuts from Pinus pinea L. Journal of Food Engineering.110, 294-297. |
| [11] | Lorestani, A.N., Tabatabaeefar, A. (2006). Modeling the mass of kiwi fruit by geometrical attributes. International Agrophysics. 20(2), 135-139. |
| [12] | Lorestani, A.N., Ghari, M. (2012). Mass Modeling of Fava bean (vicia faba L.) with Some Physical Characteristics. Scientia Horticulturae. 133(6), 6-9. |
| [13] | Suthar, S.H., & Das, S.K. (1996). Some physical properties of karingda[Citrus lanatus (thumb) mansf] grains. Journal of Agricultural Engineering Research, 65(1), 15–22. |
| [14] | Mohsenin, N.N. (1986). Physical properties of Plant and Animal Materials. Second revised. Gordon and Breach Sci. Publ., New York. |
| [15] | Lorestani, A.N., Azami, H., & Amirian, Y. (2011). Some Physical Properties of Oak (Quercus Persica) and Modeling the Mass of Oak by Physical Attributes. Proceedings of the 6th CIGR Section VI International Symposium “Towards a Sustainable Food Chain” Food Process, Bioprocessing and Food Quality Management, Nantes, France - April 18-20, 2011. |
| [16] | Tabatabaeefar, A., Vefagh-Nematolahee, A., & Rajabipour, A. (2000). Modeling of orange mass based on dimensions. Journal of Agricultural Science and Technology, 2(4), 299-305. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML