1. Introduction

The use of wood as a structural element in Brazil has grown over the last years due to researches headed for turning it into a more competitive material in comparison with other materials used in structure construction, such as steel and concrete([1]). However, the existence of gaps in the national standards combined with the lack of knowledge by building professionals about its mechanical properties contribute to limit its potential for use in constructions, being found mostly in the form of struts, concrete formworks and so on.

Among the many solutions wood can offers its outstanding use as natural or round form, having the great advantage of not being processed, as it is the case of sawn wood, which can work as structural elements such as beams, columns, aerial electric distribution poles and others. However, the national standard that deal with round timber elements are mainly headed for the pole market, being in force for at least twenty years without technical revision.

The Brazilian standard NBR 6231[2] prescribes theclamped cantilever beam model for the calculus of the longitudinal modulus of elasticity, which is a destructive method.

The Brazilian standard NBR 8456[3] only sets conditions for preparing and receiving Eucalyptus poles preserved under pressure, which is commonly used in overhead power distribution networks.

The Brazilian standard NBR 8457[4] describes poles of preserved Eucalyptus to be used in overhead power distribution networks, specifying the pole length, type, nominal strength, maximum deflection, length among others.

Technical standard NBR 6122[5] recommends the use of standard NBR 7190[6] to calculate the strength of timber piles, the latter being limited to destructive tests using small and clear specimens, even being convenient the use of the structural piece to determine their mechanical properties.

In countries where wood is traditionally used, it is possible to find a wide range of standards for many different purposes. Not only, the extensively use of wood through years but also the research experiences contribute to the large amount of information found in those documents.

Characterization, specification and standardization of experimental methods for structural-sized pieces of wood are usually done based on international standards[7-11]. According to these standards, the modulus of elasticity can be calculated by either using three and four point bending or clamped cantilever beam methods. It is noteworthy that equations used to determine the modulus of elasticity of round elements consider the hypothesis of truncated-conical geometry, based on one or two circumference values which are used to calculate its moment of inertia.

With focus on the use and study of strength and stiffness properties of structural round timber, a number of studies can be mentioned[12-23].

Miná[22] has shown a theoretical and experimental study of timber piles, including the instrumentation for timber pile foundations of a wooden bridge, in order to generate design recommendations for short-span wooden bridges. An equation to calculate the modulus of elasticity of round elements based on the Virtual Work Principle (VWP) was also presented, considering the basis, medium and top diameter values measured along the piece.

Zangiácomo and Rocco[23] evaluated the L/D ratio between length (L) and diameter (D) for correctly applying the Euler-Bernoulli theory beam to Pinus elliottii and Pinus caribea round timber structural elements, finding acceptable ratios of 12 and 15 respectively. Pinus pieces showing these ratios or higher values are free from shear influence on the deflection calculus.

Characterization of structural-sized wood elements was also performed by non-destructive tests, aimed at determining the physical and mechanical properties of a structural element without changing its usability[14]. Non-destructive testing has the advantage of not needing specimen extraction, enabling the study of its structural integrity[24,25], which is normally done by transverse vibration and ultrasound techniques[26-35].

As explained above, normative characterization of round wood structural pieces is carried out by using destructive methods. Non-destructive methods are basically ultrasound and transverse vibration, which do not require the use of mechanical testing. This study aims to present a non-destructive approach to determine the longitudinal modulus of elasticity of round timber structural beams, based on the three-point static bend testing under small-displacement conditions. The L/200 and L/300 ratios were used as displacement limiting values, being L the pieces length, expressed in centimetre (cm).

2. Materials and Methods

In order to determine the longitudinal modulus of elasticity, 16 round pieces of Pinus caribaea were used, having an average length of 580cm and an average taper of 0.01.

Round pieces obey the L/D_eq≥21 ratio[23] to validate the use of the Euler-Bernoulli beam theory, being L the length and D_eq the equivalent diameter, measured at the midpoint of the element, assuming that the sections are perfectly circular, the diameters vary linearly along its length and the maximum displacement of the element which occurs at the point of application of the force (small taper).

In this study, the modulus of elasticity is calculated by Equation 1, which is derived from the three-point static bending structural model (Figure 1), adapted from Brazilian standard[6] for circular section structural pieces, neglecting the load and displacement variations, being (F) the force found for the (δ) L/300 and L/200 displacements. It must be highlighted that the L/200 ratio is the measurement defined by standard[6] that ensures physical and geometrical linearity for wooden pieces (small displacement), whereas the L/300 is a more conservative measurement, quoted to replace the L/200 measurement in the new version of standard[6].

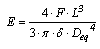(1)

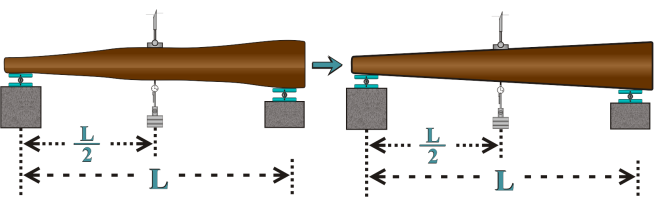Figure 1. Three-point static bending test

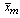Statistical equivalence between the values found from E_L/300 (longitudinal modulus of elasticity calculated for the L/300 measurement) and E_L/200 (longitudinal modulus of elasticity calculated for the L/200 measurement) for structural round timber is evaluated by using a confidence interval for the medians, which is expressed by Equation 2, being μ the difference between population means, the difference between sample means, n the sample size, S_m the difference between sample standard deviations, and t_α/2,n-1 the tabulated value from Student’s t-distribution with n-1 degrees of freedom and significance level α.

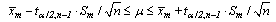(2)

Anderson-Darling test was used to see whether the sets of values for the modulus of elasticity were normally distributed, validating the confidence interval presented herein.

3. Results and Conclusions

The moduli of elasticity of E_L/300 and E_L/200 founded for Pinus caribaea structural round timber are shown in Table 1.

Table 1. EL/300 e EL/200 values. Peças EL/300 (MPa) EL/200 (MPa) Peças EL/300 (MPa) EL/200 (MPa) 1 6324 6819 10 6502 6102 2 8689 8355 11 9527 9121 3 9521 9931 12 8675 8972 4 8783 8466 13 8322 8056 5 7468 7927 14 6584 6936 6 7430 7889 15 10206 9570 7 8257 7693 16 9481 9079 8 7688 7920 17 6539 6924 9 7321 6839 18 5820 5977

P-values founded for the moduli of elasticity EL/300 and EL/200 are respectively 0.521 and 0.679, both greater than 0.05, confirming the hypothesis of normal distribution and validating the use of the confidence interval[36], as shown in Figure 2.

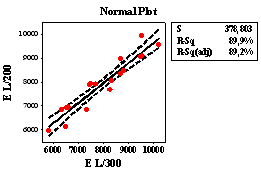Figure 2. Normal plot between EL/300 e EL/200

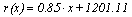The graph of linear regression between the elasticity values for the two displacement limits is shown in Figure 3, whose adjustment equation and correlation coefficient (R2) are respectively and 0.89.

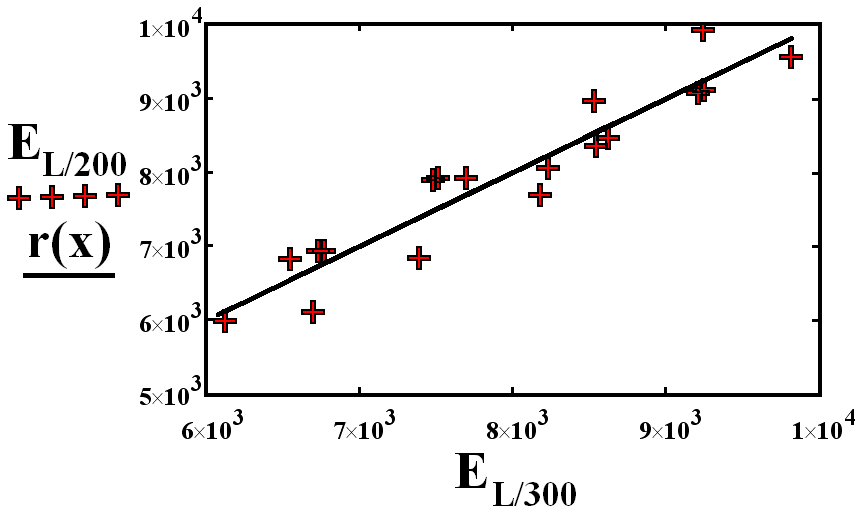Figure 3. Linear regression between EL/300 e EL/200

The confidence interval between E_L/300 and E_L/200 is -800.45862.77, being statistically equivalent by the relevance of zero to the subset founded. This implies that static three-point bending testing combined with the use of Equation 1 under the L/300 and L/200 displacement conditions led to equivalent values for the modulus of elasticity of the evaluated timbers. This result cannot be extended to other wood species, further research is still needed.

In general terms, the use of the three-point static bending test appears as an alternative way to determine the longitudinal modulus of elasticity of round timber structural beams, since it imposes less operational difficulties than those of the cantilever beam clamped model, as proposed by the Brazilian standard[2].

The ratio L/D_eq≥21[23] allows to use the Euler Bernoulli beam theory to calculate the deflections with no shear effect which were used to determine the modulus of elasticity. In addition it was possible to use the three point bending test, even when shear efforts exist at the applied load.

The restriction of displacements (L/200 and L/300) provide the use of non-destructive methodology to determine the longitudinal modulus of elasticity of timber beams, instead of the Brazilian standard[6] which is based on a destructive method using small sample size.