1. Introduction

Yield is a complex character and is known to be associated with a number of component characters and is highly affected by environmental variations. These characters are themselves interrelated. Such inter-dependence of the contributing factors affect their direct relationship with yield, thereby making correlation coefficients unreliable as selection indices (Shoran, 1982). Thus, specification of causes and measuring the relative importance of each of the yield components can be achieved by using the method of path analysis, as a mean of separating the direct effects from the indirect ones through other characters. Several path coefficient analysis have been conducted in guar, using grain-type cultivars (Tikka, 1975; Chaudhary and Singh, 1976; Bhard- waj et al., 1981; Sohoo and Bhardwaj, 1985; Henary et al., 1986; Stafford and Seiler, 1986).

Breeding and selection programmes often encompass several characters simultaneously (Hill et al, 1998). When considering several traits, it is desirable to choose individuals with the best combination of these traits. The basis for such a selection is selection index, which takes, into account a combination of traits according to their relative weight. Thus each individual trait has an index value (score) and selection is based on the sum of the scores (values) of the different traits. Gain from selection for any given trait is expected to decrease as additional traits are included in the index, so the choice for traits to be include must be done objectively (Hallauer and Miranda, 1982). In guar, selection indices have been effectively used in identifying some traits as selection criteria to improve seed yield. Choudhary and Joshi (1996); Elsyed (1999), concluded that maximum efficiency of selection was obtained when all the important yield components were included in the index.

To provide basis for selection and yield improvement in guar, this study investigated the interrelationship between yield and its components, determined the relative contribution of the different yield components to the final yield and estimated the expected genetic advances and relative efficiencies.

2. Materials and Methods

Sixteen genotypes of guar (Cyamopsis tetragonoloba L.), fourteen inbred lines and two commercial varieties HFG53 and HFG408, were evaluated during 1998 crop season under rain-fed conditions at Kazgeil, North Kordofan State, Sudan. Seeds of these genotypes were offered by Dr.Abdel Wahab Hassan Abdalla, Department of Agronomy, Faculty of Agriculture, University of Khartoum, Sudan.

Ten plants from each plot were randomly selected from the middle ridges for collecting data on number of fruiting nodes/main stem, number reproductive branches/plant, number pods/plant, number seed/pod, 1000 seed weight (g) and seed yield/plant (g).

The collected data were subjected to analysis of variance according to the method described by Gomez and Gomez (1984), and covariance according to Singh and Chaudhary (1979). Then the genotypic and phenotypic correlation coefficients were determined for all possible pairwise combinations between the characters, according to Miller et al. (1958).

Path coefficient analysis was calculated, following the procedure suggested by Dewey and Lu (1959). It was used for partitioning the genotypic correlation between seed yield and five of its components into direct and indirect effects. The characters included in the model were:

Number of fruiting nodes/main stem

Number of reproductive branches/plant

Number of pods/plant

Number of seed/pod

1000 seed weight (g)

seed yield/plant (g)

The path coefficients of the five traits were obtained by simultaneous solution of the following equations:

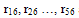are the genotypic correlation coefficients of the five characters involved in the model with seed yield per plant (6).

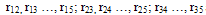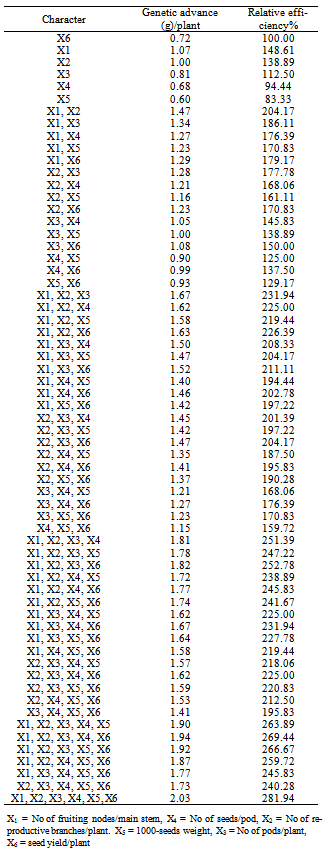
and r₄₅ are genotypic correlation coefficients of the possible pair wise combinations of the five characters. 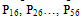are the path coefficients (direct effects) of the five traits on seed yield/plant (6).

The residual effect was determined, following Singh and Chaudhary (1979), by substituting the estimated path coefficients and the genotypic correlations in the following equations.

Where:

Px: is the path coefficient of (x) variables, not included in the model, on seed yield per plant (6).

Different selection indices were formed using the six characters, and seed yield/plant was used as the ultimately desired product. Different phenotypic weights (b’s) were assigned to the six parameter. These weights were computed according to the method suggested by Robinson et al. (1951), in which a set of simultaneous equations, constructed from the genotypic and phenotypic variances and covariance’s of the characters involved, was solved, as follows.

Where:

P: is the phenotypic variance or covariance.

g: is the genotypic variance or covariance.

P₁₁: is an estimate of the phenotypic variance of character x₁.

P₁₂: is an estimate of phenotypic covariance between characters x₁ and x₂.

g_1y: is an estimate of the genotypic covariance between characters x₁ and x_y. (yield = dependent character).

b: is the selection weight.

b₁: is the selection weight for the character x₁.

b_{2 :} is the selection weight for the character x₂.

The standard formula for selection index is:

A number of selection indices were constructed. They are composed of indices that are based on single character and those based on the possible combinations of the characters.

The expected genetic advance of these indices was determined according to the formula suggested by Robinson et al. (1951)

Where:

k: is the selection differential in standard units, its value is 2.06 when selection intensity is 5%.

b: is the selection weight.

g: is the genotypic variance or covariance.

The estimates of genetic advance from selection were in grams of seed yield per plant. Then they were expressed as percentage of the genetic progress obtained from seed yield per plant alone, which was assumed to be 100%, and it was used to compare the relative efficiencies of the different selection indices.

3. Results and Discussion

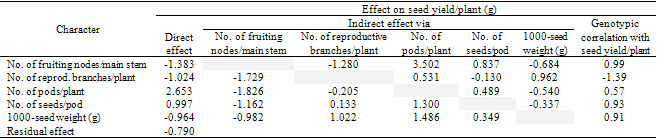
The results of the path analysis are given in Table 1 and Figure 1. The number of pods/plant exerted the highest positive direct effect (2.653) on seed yield/plant. It was followed by the number of seeds/pod (0.997). This result reflects the importance of these characters as yield components. Similar findings were reached by Stafford and Seiler (1986). Furthermore, the highest direct effect of number of pods/plant was accompanied with maximum positive indirect effects of all other characters, via number of pods/plant, indicating that the number of pods/plant is the most important component trait of yield in guar.

Although number of pods/plant exerted the highest positive direct effect, it had negative indirect effects on seed yield via number of fruiting nodes/main stem (-1.826), number of reproductive branches /plant (-0.205) and 1000 seed weight (-0.54). Its positive direct effect (2.653) in addition to its positive indirect one, through number of seeds/pod (0.489), exceeded its negative indirect effects and this was reflected in its significant positive genotypic correlation (0.57) with seed yield/plant.

Table 1. Path Coefficient Analysis of the Direct and Indirect Effects of Five Yield Components and their Genotypic Correlation Coefficients with Seed Yield/Plant with in Guar at Kazgeil, Northern Kordofan, State, Sudan, in 1998/99 Season

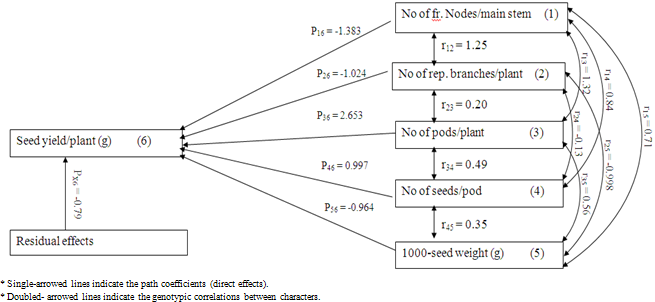Figure 1. Diagram of the direct and indirect relationships of seed yield/plant with its components at the genotypic level, using path coefficient analysis at Kazgeil, Northern Kordofan, State, Sudan, in 1998/99 season

Number of fruiting nodes/main stem exerted the highest negative direct effect (-1.383) followed by number of reproductive branches/plant (-1.024) and 1000 seed weight (-0.964). The result for number of fruiting nodes/main stem is similar to that of Abdelmula and Abdalla (1994), in faba bean, whereas the result for 1000 seed weight is in contradiction with the findings of Stafford and Seiler (1986), Bhardwaj et al. (1981) and Chaudhary and Singh (1976).

All yield components, which were selected for path analysis, had positive genotypic association with seed yield/plant except number of reproductive branches/plant which had a negative one. This negative genotypic association of number of reproductive branches/plant resulted from the dominance of its direct effect (-1.024) and indirect effects, through number of fruiting nodes/main stem (-1.729) and number of seeds/pod (-0.13), over its positive indirect effects through number of pods/plant (0.531) and 1000 seed weight (0.962). Number of seeds/pod had a negative indirect effect on seed yield/plant through 1000 seed weight. This confirms the results of Bhardwaj et al. (1981) and Stafford and Seiler (1986), in guar, Shoran (1982), in pigeonpea, Singh and Mehndiratta (1970), in cowpea and Singh and Malhotra (1970), in mungbeam.

The direct effects of number of pods/plant and number of seed/pod were of higher magnitude than those suggested by the correlation. On the other hand, the direct effect of number of reproductive branches/plant was of low magnitude than that suggested by the correlation. This phenomenon (the conflict between the correlation and the path coefficient analysis) is wide spread among the major crop plants, because correlation simply measures the apparent mutual association between the two characters without regard to the cause, where as path coefficient specifies the causes and measures their relative importance. So, it may be concluded from these findings that correlation alone may not give complete information but when used in conjunction with path coefficient analysis will give a better measure of cause and effect relationship existing between different pairs of characters. Similar conclusions were reported by many workers Dewey and Lu (1959) in crested wheatgrass, Phadnis et al. (1970) in chickpea, Singh and Mehndiratta (1970) in cowpea, Salih and Khidir (1975) in castorbean, Fadlalla (1994) in wheat; Gasim and Khidir (1998b) in rosselle. The expected genetic advances in seed yield and the relative efficiencies of different selection indices, involving the seed yield/ plant as an independent variable index and five yield components, singly and in different combinations are shown in Table 2. The individual trait indices, viz., number of fruiting nodes/main stem, number of reproductive branches/ plant and number of pods/plant had the highest relative efficiencies (148.61, 138.89 and 112.5 percent, respectively. This means that these traits were more efficient in determining the genotypic value of a genotype than selection based on seed yield/plant alone, Also it indicates their importance as yield attributes. This finding was further confirmed by the fact that whenever number of fruiting nodes/main stem and number of reproductive branches/plant were added to or replaced other traits in a selection index, the efficiency of such index was tremendously improved. A similar pattern, though not to the same extent as that of number of fruiting nodes/main stem and number of reproductive branches/plant, was observed for number of pods/plant. The minimum genetic advances 68% and 60% and the minimum relative efficiencies 94.44 and 83.33 percent were obtained by the indices having single traits, viz., number of seeds/pod and 1000 seed weight, respectively. This is in accordance with Elsyed (1999), who reported that number of seeds/pod and 1000 seed weight had low efficiencies of 44 and 60 percent, respectively. Furthermore, when 1000 seed weight was added to or replaced another character in a selection index, the relative efficiency of such an index was drastically reduced. Therefore, it could be concluded that 1000 seed weight is an inefficient selection criterion for the improvement of seed yield. Similar results were obtained by Choudhary and Joshi (1996).

In this study, the expected genetic advance and the relative efficiency of the index was increased with the increase in the number of characters involved. The selection index involving all the six characters exhibited the highest expected genetic advance (2.03 g/plant) and the maximum relative efficiency (281.94%). Similar conclusions were obtained by Mital and Thomas (1969), Choudhary and Joshi (1996); Elsyed (1999), in guar, Abdelmula and Abdalla (1993), in faba bean and Ibrahim (2002), in rosselle. Although this index exceeded the straight selection based on seed yield/plant per se by 181.94% the genetic advance was relatively low.

In general, the equal values of genetic advance and relative efficiency of two or more selection indices in the same or different order/s indicate that the trait/s which comprised a selection index had the same weight as its comparable one/s. e.g, the two trait selection index of number of pods/plant and 1000 seed weight scored the relative efficiency of 138.89% which is equal to the relative efficiency of the individual trait index of number of reproductive branches/plant. This means that number of reproductive branches/plant weight the two traits, number of pods/plant and 1000 seed weight together in selection for seed yield, in this study. This result was supported by the equal values of the two- trait selection index (number of fruiting nodes/main stem and number of reproductive branches/plant) and the three-trait one ( number of fruiting nodes/main stem, number of pods/plant and 1000 seed weight). A similar finding was obtained for the individual trait index (number of reproductive branches/plant) and the two-trait index (number of pods/plant and seed yield/plant it self).

Table 2. Selection Index, Expected Genetic Advance and Relative Efficiency in Guar (Cyamopsis tetragonoloba L.) at Kazgeil in 1998/99 Rainy Season

4. Conclusions

It could be concluded from this study that number of pods/plant and number of seeds/pod were the most important yield components, as pointed out by path analysis and selection index. These components were positively associated with each other and with yield, suggesting that simultaneous improvement in these characters might be easy.