-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Agriculture and Forestry
p-ISSN: 2165-882X e-ISSN: 2165-8846
2011; 1(1): 1-8
doi: 10.5923/j.ijaf.20110101.01
Effect of the Representative Source Area for Eddy Covariance Measuraments on Energy Balance Closure for Maize Fields in the Po Valley, Italy
Daniele Masseroni , Chiara Corbari, Marco Mancini
Dipartimento di Ingegneria Idraulica, Ambientale, Infrastrutture Viarie e Rilevamento, Politecnico di Milano, P.zza Leonardo da Vinci, 32, 20133, Milano, Italy
Correspondence to: Daniele Masseroni , Dipartimento di Ingegneria Idraulica, Ambientale, Infrastrutture Viarie e Rilevamento, Politecnico di Milano, P.zza Leonardo da Vinci, 32, 20133, Milano, Italy.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper has as main objective to show the effect of the representative source area for eddy covariance measurements (called footprint) on energy balance closure. Energy balance closure was evaluated by a statistical regression of turbulent energy fluxes (sensible and latent heat) against available energy (net radiation and soil ground heat flux). The footprint was calculated using an approximate analytical model based on a combination of Lagrangian stochastic dispersion model and dimensional analysis. The data were measured by two eddy covariance towers located on maize fields in Landriano (PV) and Livraga (LO) at the Po Valley, Italy. The main results obtained using only the flux data which have a source area included into the cultivated field shows that there is a slight improvement on the energy balance closure. The stability conditions of the atmosphere plays a fundamental role on the slope of the linear regression and on footprint size, in particular way, it is shown when the energy balance closure is analysed for different sectors of the field in function of the wind directions.
Keywords: Footprint, Energy Balance Closure, Eddy Covariance Method
Cite this paper: Daniele Masseroni , Chiara Corbari, Marco Mancini , "Effect of the Representative Source Area for Eddy Covariance Measuraments on Energy Balance Closure for Maize Fields in the Po Valley, Italy", International Journal of Agriculture and Forestry, Vol. 1 No. 1, 2011, pp. 1-8. doi: 10.5923/j.ijaf.20110101.01.
Article Outline
1. Introduction
- The eddy covariance technique is generally used to estimate turbulence fluxes of mass and energy to and from surfaces. A difficult but important issue remains to quantify estimates of the uncertainty of the reported flux values. These fluxes are in fact complex processes, and the estimates result from various measurements and calculations as well as numerous explicit and implicit assumptions[4,23]. Hence, documenting the absolute accuracy of these values is somewhat problematic. However, one simple measure of internal consistency is to check for conservation of energy. So the sum of the turbulence fluxes of sensible and latent heat should balance the available energy[9]. The surface energy balance may be written as in (1).
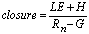 | (1) |
2. Theoretical Background
2.1. Eddy Covariance Technique
- The turbulence of the air flow can be described, using the Reynold’s hypothesis, subdividing wind speed and the scalar quantities in a mean component and in a fluctuant component (2).
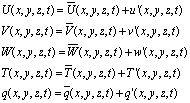 | (2) |
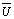 ,
, 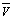 ,
, 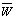 ,
, 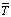 and
and 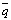 represents the mean components and the u’,v’,w’,T’ and q’ represents the fluctuant components. It is important to remark that these components are a function of the spatial position (x,y,z) and time (t). The eddy covariance method determines the surface fluxes as the sum of turbulent eddy-fluxes, measured above the surface, and the flux divergence between the surface and the eddy covariance measurement level[2]. The basic equations to estimate latent and sensible heat fluxes, (3) and (4), are comparatively simple.
represents the mean components and the u’,v’,w’,T’ and q’ represents the fluctuant components. It is important to remark that these components are a function of the spatial position (x,y,z) and time (t). The eddy covariance method determines the surface fluxes as the sum of turbulent eddy-fluxes, measured above the surface, and the flux divergence between the surface and the eddy covariance measurement level[2]. The basic equations to estimate latent and sensible heat fluxes, (3) and (4), are comparatively simple.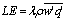 | (3) |
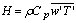 | (4) |
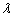 is the vaporization latent heat,
is the vaporization latent heat, 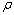 the air density and
the air density and 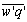 the covariance between vertical wind velocity component and scalar concentration of vapor in the air. Cp is the specific heat at constant pressure and
the covariance between vertical wind velocity component and scalar concentration of vapor in the air. Cp is the specific heat at constant pressure and 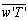 is the covariance between vertical wind velocity component and scalar temperature.The covariance of the vertical wind velocity and scalar quantities can be determined by (5):
is the covariance between vertical wind velocity component and scalar temperature.The covariance of the vertical wind velocity and scalar quantities can be determined by (5):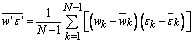 | (5) |
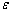 represents a generic scalar quantity and N the total number of data. The energy balance closure can be written as (6):
represents a generic scalar quantity and N the total number of data. The energy balance closure can be written as (6):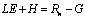 | (6) |
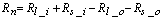 | (7) |
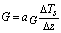 | (8) |
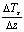 and the thermal molecular conductivity aG. The aG values in function of the different types of ground surface can be found in[18]. On summer days, the ground heat is about 50-100 Wm-2[6]. LE, H, G and Rn have a totally different representative source areas. LE and H are turbulent fluxes and their representative source area is defined by the footprint size[10]. It depends to the turbulent characteristics of the atmosphere and many other variables for example roughness, wind velocity, measurement height and so on[6]. Its value goes from some meters square to hectares. For Rn the representative source area is characterized by the radiometer field of view and it depends, in particular way, on the measurement height. The net radiometer is located on the tower at the height of about 4 meters (see Section 3) and its field of view can be considered of about 50m2 (for an angle of 45°). Ground heat flux (G) is usually very small respect to the other energy fluxes, ranging from 5 to 40 % of net radiation but this flux is the one with the highest uncertainty in its estimate that can reach en error up to 50%[6]. Moreover it is measured with an instrument with the smallest source area that can be up to two orders of magnitude lower than latent and sensible heat fluxes footprints; however, in literature it is assumed that the net radiation and ground heat flux measurements are representative for the total cultivated field[6].
and the thermal molecular conductivity aG. The aG values in function of the different types of ground surface can be found in[18]. On summer days, the ground heat is about 50-100 Wm-2[6]. LE, H, G and Rn have a totally different representative source areas. LE and H are turbulent fluxes and their representative source area is defined by the footprint size[10]. It depends to the turbulent characteristics of the atmosphere and many other variables for example roughness, wind velocity, measurement height and so on[6]. Its value goes from some meters square to hectares. For Rn the representative source area is characterized by the radiometer field of view and it depends, in particular way, on the measurement height. The net radiometer is located on the tower at the height of about 4 meters (see Section 3) and its field of view can be considered of about 50m2 (for an angle of 45°). Ground heat flux (G) is usually very small respect to the other energy fluxes, ranging from 5 to 40 % of net radiation but this flux is the one with the highest uncertainty in its estimate that can reach en error up to 50%[6]. Moreover it is measured with an instrument with the smallest source area that can be up to two orders of magnitude lower than latent and sensible heat fluxes footprints; however, in literature it is assumed that the net radiation and ground heat flux measurements are representative for the total cultivated field[6]. 2.2. The Hsieh’s Model
- The Hsieh’s model [10] is based on the equation (9).
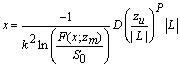 | (9) |
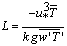 | (10) |
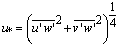 | (11) |
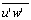 and
and 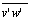 are the covariance between vertical velocity component and planar (longitudinal and transversal) components of the wind, and zu is defined by (12) where z0 represents the surface roughness.
are the covariance between vertical velocity component and planar (longitudinal and transversal) components of the wind, and zu is defined by (12) where z0 represents the surface roughness. 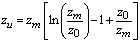 | (12) |
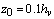 | (13) |
3. Study Sites and Instruments
- Experimental data were obtained by two micrometeorological stations utilized to measure evapotranspiration fluxes in maize fields, one in Landriano (PV) (45.19 N, 9.16 E, 87 m a.s.l) and another one in Livraga (LO) (45.11 N, 9.34 E, 60 m a.s.l) (Figure 1). The distance between the stations is about 100 Km and they are located at the Po valley.
 | Figure 1. Eddy covariance tower at Livraga (LO). |
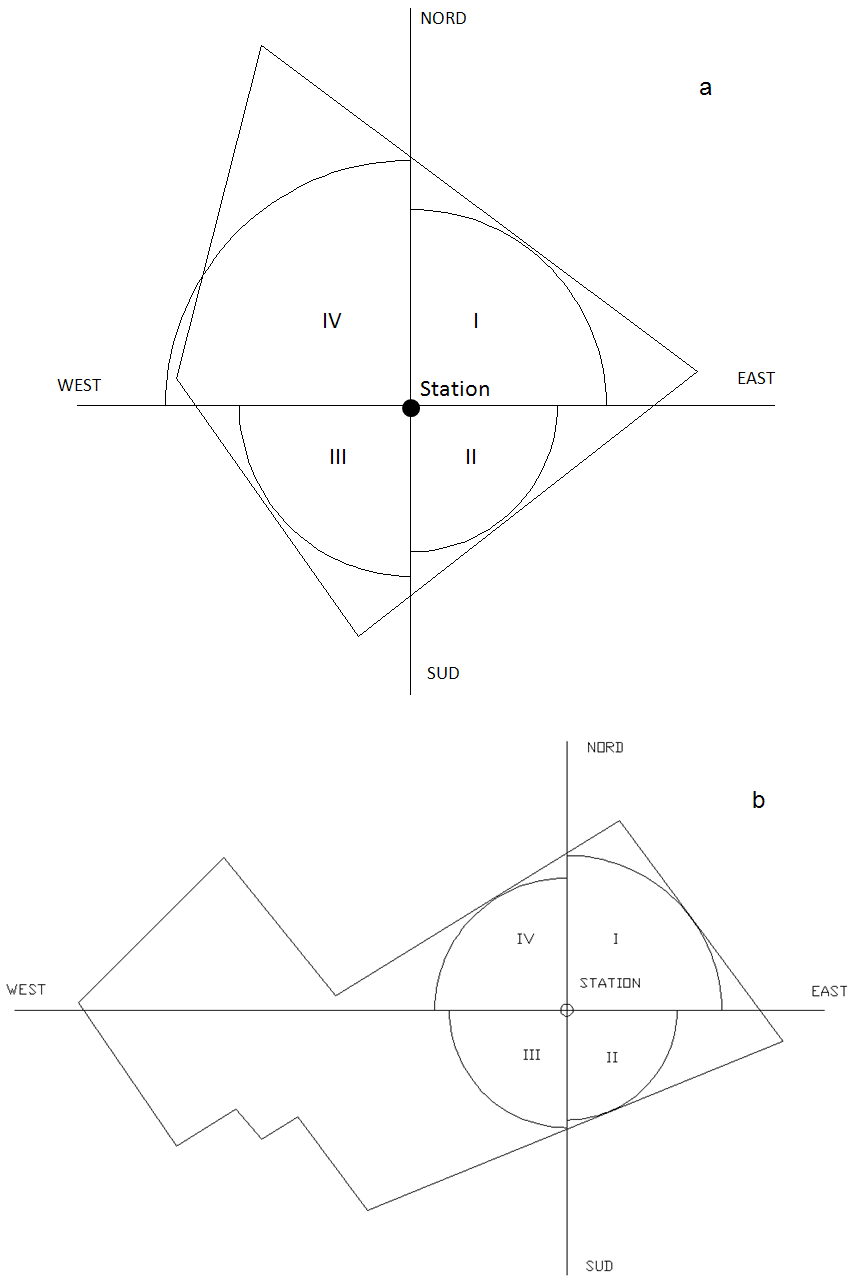 | Figure 2. a. Landriano field, b. Livraga field. Subdivision in sectors. |
4. Method
- The objective of this work is to understand the influence of the representative source area for eddy covariance measurements on energy balance closure. The first step was to subdivide Landriano and Livraga fields in four different sectors along geographic directions (Figure 2a and b) so that the data were subdivided in four classes of 90 degree each depending on wind direction. For each sector it was definite a radius of a source area which is included at least 95% into the field. In Table 1 the radius value taken for each sector is shown.
| |||||||||||||||||||||
5. Results and Discussion
- The results show that the slope of the energy balance closure increases slightly if the data without a footprint size compatible with the field dimension were deleted. In Figure 3 and 4 are shown the energy balance closure respectively for Landriano and Livraga site. In Figure 3a and 4a are represented the energy balance closure for all data set, while in Figure 3b and 4b the energy balance closure is calculated using only the footprint compatible data. For Landriano site, the slope of the linear regression has a slight improvement of about 0.40% and for the linear correlation coefficient of about 3.8%. For Livraga site, the difference in slope is 0.33% and in R2 is equal to 4.24%
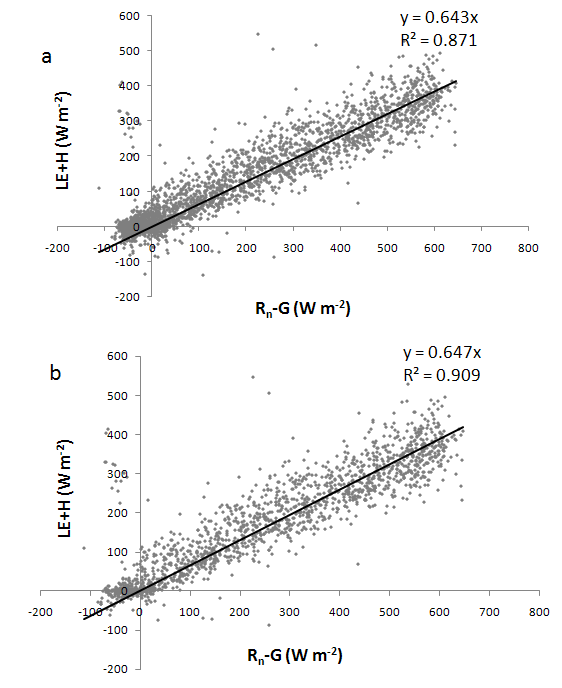 | Figure 3. Landriano site. a. energy balance closure with all data. b. energy balance closure using the data with a footprint compatible with field dimension. |
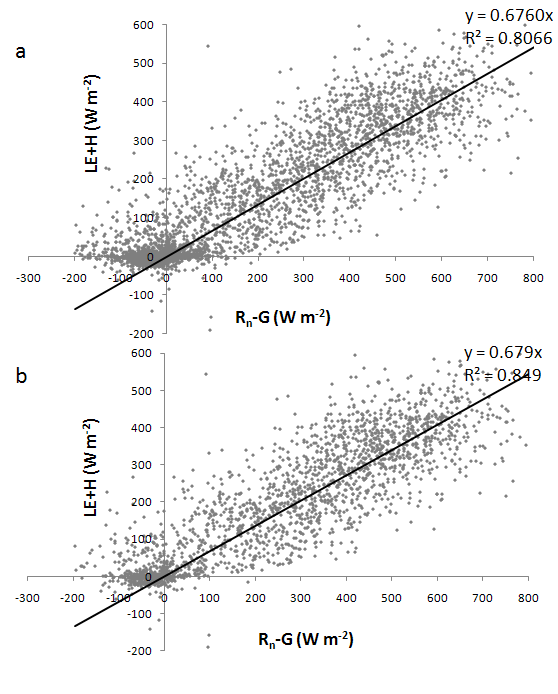 | Figure 4. Livraga site. a. energy balance closure with all data. b. energy balance closure using the data with a footprint compatible with field dimension. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||
5.1. Energy Balance Closure for Field Sectors
- In Figure 5 and 6 the energy balance closure and the footprint size for the different field sectors as a function of the wind directions are shown. In Figure 5A and 6A the energy balance closure taking into account all data set is represented, while in Figure 5B and 6B the energy balance closure is made using only the data with a footprint length compatible with the field dimension. The energy balance closure characterization for different sectors is necessary to understand how each sector field takes part on total energy balance closure. In fact in some cases it is present an m value improvement (sectors I, II and IV for Landriano, and sectors I, III and IV for Livraga) but in other cases the m value decrease (sector III for Landriano and sector II for Livraga).In Table 5 the percentages of improvement of the slope of linear regression and R2 for the data which have a footprint size included into the field are represented. In general in Landriano and Livraga sites for almost all the sectors a slight improvement in both m and R2 values is presented. In Figure 5 and 6 (C and D) the footprint sizes for different classes subdivided in unstable and neutral conditions of the atmosphere are represented. During convective conditions the source area lengths are distributed over all the footprint classes, while in neutral conditions only some classes have the most part of the footprint values.
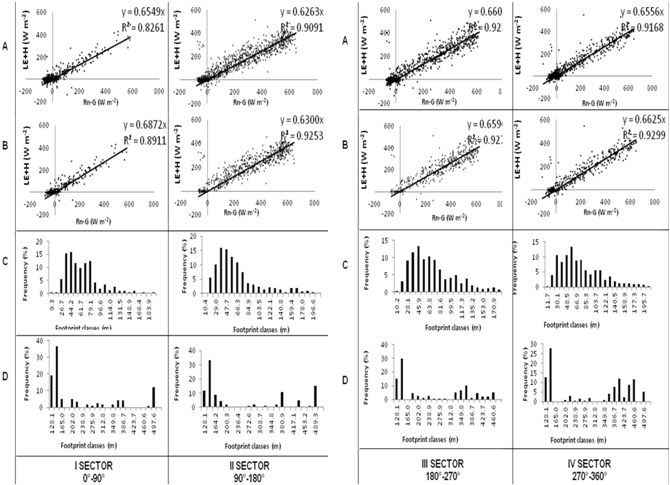 | Figure 5. Landriano site. A. Energy balance closure with all data. B. Energy balance closure using the data which have a footprint size less than field dimension. C. Footprint length for unstable conditions of the atmosphere. D. Footprint length for neutral conditions of the atmosphere. |
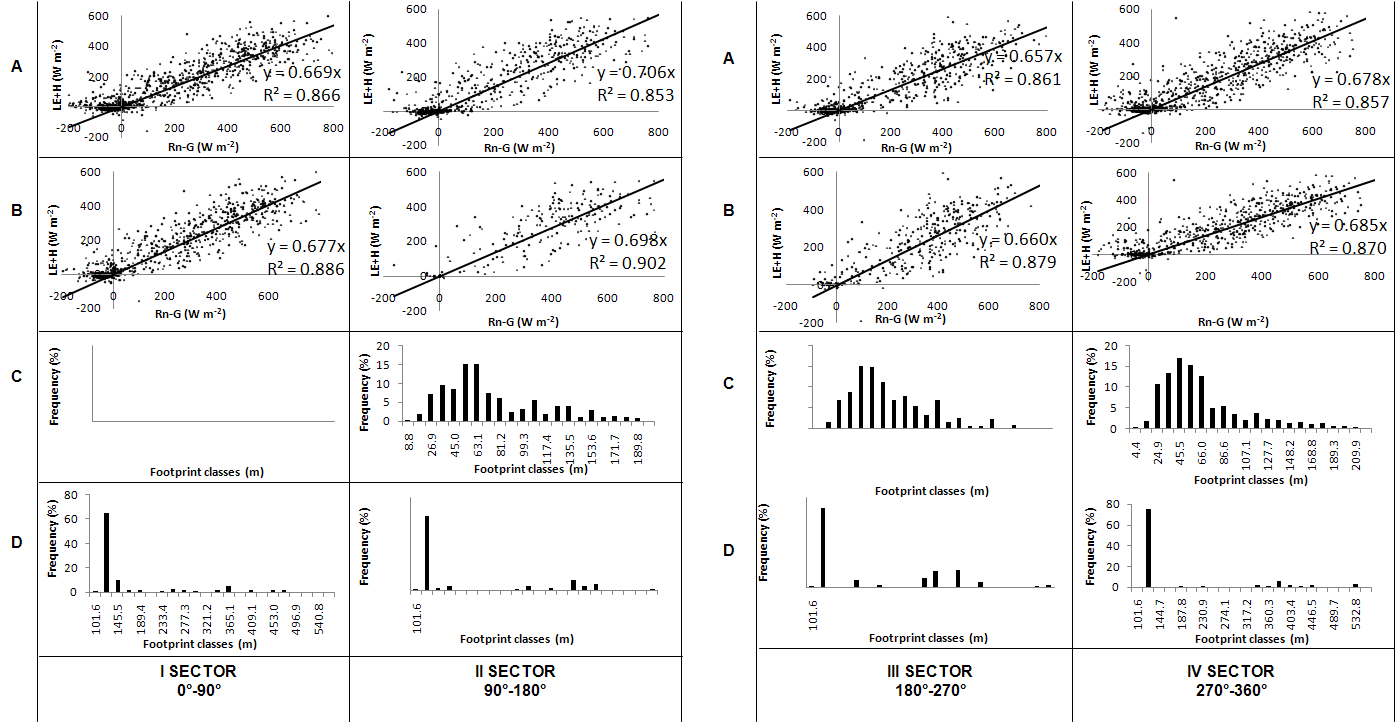 | Figure 6. Livraga site. A. Energy balance closure with all data. B. Energy balance closure using the data which have a footprint size less than field dimension. C. Footprint length for unstable conditions of the atmosphere. D. Footprint length for neutral conditions of the atmosphere. |
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
6. Conclusions
- In this work the effect of the source area of eddy covariance measurements on energy balance closure for maize fields in Po Valley has been shown. The energy balance was evaluated for different conditions of the atmosphere and to understand their effects on the closure, the slope of the linear regression (m) and the linear correlation coefficient (R2) were calculated. The results show that the eddy covariance stations works only in unstable and neutral conditions. In stable conditions the atmospheric boundary layer structure is quite laminar and the turbulent heat fluxes measured by the eddy tower are uncorrected. During neutral conditions, a lot of data have to be deleted because the turbulent fluxes source representative area exceeds the field dimension. In Landriano and Livraga site the effect of the representative source area for eddy fluxes leads to a slight improvement into the energy balance closure, instead, the stability conditions of the atmosphere play a fundamental role for the determination of the slope of the linear regression curve. The study on the representative source area for eddy covariance measurements is important to understand if the station position into the field is correct, the energy balance closure makes for different sector in function of the wind directions shows that in Landriano and Livraga sites the eddy covariance towers are located correctly and the latent and sensible heat measured are representative of the maize fields.
ACKNOWLEDGES
- This work was funded in the framework of the ACQWA EU/FP7 project (grant number 212250) “Assessing Climate impacts on the Quantity and quality of WAter”, the framework of the ACCA project funded by Regione Lombardia “Misura e modellazione matematica dei flussi di ACqua e CArbonio negli agro-ecosistemi a mais” and PREGI (Previsione meteo idrologica per la gestione irrigua) founded by Regione Lombardia. The authors thank the University of Milan – Dipartimento di Idraulica Agraria for the collaboration given in managing Landriano eddy covariance station.
References
| [1] | Baldocchi, D. and Rao, K., 1995. Intra-field variability of scalar flux densities across a transition between desert and an irrigated potato field . Boundary Layer Meteorology, 76, 109-136 |
| [2] | Barr, A., Morgenstern, K., Black, T., McCaughey, J. and Nesic, Z., 2006. Surface energy balance closure by the eddy-covariance method above three boreal forest stands and implications for the measurement of CO2 flux. Agricultural and Forest Meteorology , 140, 322-337 |
| [3] | Calder, K., 1965. Concerning the similarity theory of A. S. Monin and A. M. Obukhov for the turbulent structure of the thermally stratified surface layer of the atmosphere. Quarterly Journal of the Royal Meteorological Society , 92, 141-146 |
| [4] | Culf, A., Foken, T. and Gash, J., 2004. The energy balance closure problem, in: A new prospective on an iteractive system. Kabat, P., Claussen ,M., Vegetation, Water, Humans and Climate, Springer, Berlin, 159-166 |
| [5] | Dyer, A., 1963. The adjustament of profiles and eddy fluxes. Quart. J. R. Meteorol.Soc. ,89, 276-280 |
| [6] | Foken, T., 2008. Micrometeorology. Springer, Berlin, 306 |
| [7] | Foken, T., Wimmer, F., Mauder, M., Thomas, C. and Liebhetal, C., 2006. Some aspects of the energy balance closure problem. Atmos. Chem. Phys. , 6, 4395-4402 |
| [8] | Gash, J., 1985. A noteon estimating the effect of a limited fetch on micrometeorological evaporation measurements. Boundary Layer Meteorology , 35, 409-413 |
| [9] | Hipps, L., Prueger, J., Eichinger, W. and Kustas, W. Relations between enviormental conditions and the ability to close energy balance. In Proceedings of the 27th Conference on Agricoltural and Forest Meteorology, May 22-25, 2006, San Diego, CA. 2006 CDROM |
| [10] | Hsieh, C., Katul, G. and Chi, T., 2000. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Advanced in water researc , 23, 765-772 |
| [11] | Hsieh, C., Katul, G., Schieldge, J., Sigmon, J. and Knoerr, K., 1997. The Lagrangian stochastic model for fetch and latent heat flux estimation above uniform and nonuniformterrain. Water Resources Research , 33, 427-438 |
| [12] | Kljun, N., Rotach, M. and Schmid, H., 2002. A 3D bacward Lagrangian footprint model for a wide range of buondary layer stratifications. Boundary Layer Meteorology , 103, 205-226 |
| [13] | Liu, H., Peters, G., & Foken, T. (2001). New equations for sonic temperature variance and buoyancy heat flux with an omnidirectional sonic anemometer. Bound. Layer. Meteorology, 100, 459-468 |
| [14] | Mao, S., Feng, Z. and Michaelides, E., 2007. Large-eddy simulation of low-level jet-like flow in a canopy. Envaiormental Fluid Mechanics , 7, 73-93 |
| [15] | Markkanen, T., Steinfeld, G., Kljun, N., Raasch, S., and Foken, T. (2009). Comparison of conventional Lagrangian stochastic footprint models against LES driven footprint estimates. Atmospheric Chemistry and Physics, 9, 5575-5586 |
| [16] | Massman, W. and Lee, X., 2002. Eddy covariance flux corrections and uncertainties in long-term studies of carbon and energy exchanges. Agricoltural Forest Meteorology, 113, 121-144 |
| [17] | Schmid, H., 2002. Footprint modeling for vegetation atmosphere exchange studies: a review and prospective. Agricoltural Forest Meteorology , 113, 159-184 |
| [18] | Stull, R., 1988. An introduction to boundary layer meteorology. Dordrecht, Boston, London, 666. Kluwer Academic Publisher |
| [19] | Tanner, C. and Thurtell, G., 1969. Anemoclinometer measurements of Reynolds stress and heat transport in the atmospheric surface layer. ECOM 66-G22-F, ECOM, United States Army Eletronics Command, Research and Developement |
| [20] | Thomson, D., 1978. Criteria for the selection of stochastic models of particle trajectories in turbolent flows. Journal of Fluid Mechanic , 180, 529-56 |
| [21] | Van Ulden, A., 1978. Simple estimates for vertical diffusion from cources near the ground. Atmospheric Enviorment , 12, 2125-2129 |
| [22] | Webb, E., Pearman, G. and Leuning, R., 1980. Correction of the flux measurements for density effects due to heat and water vapour transfer. Boundary Layer Meteorology, 23, 251-254 |
| [23] | Wilson, K., Goldstein, A., Falge, E., Aubinet, M., Baldocchi, D., Berbigier, P., et al. (2002). Energy balance closure at FLUXNET sites. Agricoltural Forest Meteorology, 113, 223-243 |
| [24] | Wyngaar, J., 1990. Scalar fluxes in the planetary boundary layer. Boundary Layer Meteorology , 50, 49-79 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML