-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Geosciences
p-ISSN: 2163-1697 e-ISSN: 2163-1719
2019; 9(1): 1-7
doi:10.5923/j.geo.20190901.01

Least-Square Geothermal Models in Crustal Rocks with Non-Radiogenic and Radiogenic Heat Generation Sources in the Niger Delta Basin
G. I. Alaminiokuma1, E. S. Osegbowa2
1Department of Earth Sciences, Federal University of Petroleum Resources, Effurun, Effurun, Nigeria
2Department of Physics, Rivers State University of Science & Technology, Nkpolu-Oroworukwo, Nigeria
Correspondence to: G. I. Alaminiokuma, Department of Earth Sciences, Federal University of Petroleum Resources, Effurun, Effurun, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Geothermal models in crustal rocks with non-radiogenic and radiogenic heat generation sources were developed using temperature data from Continuous Temperature Logs in 26 wells randomly distributed across the Niger Delta Basin. Data analyses and interpretation by the method of Least-squares generated results which show that Ground Surface Temperature (GST) ranged between 5.4 and 53.5°C with a mean of 27.98°C; Geothermal Gradient (Gg) ranged between 0.37 to 3.84°C/100m with a mean of 2.14°C/100m. The mean geothermal distribution functions obtained for both the non-radiogenic and radiogenic heat generation models in the Niger Delta are T=27.983+0.0214y and T=27.983+0.0214y-2.64x10-10y2 respectively. This is very vital in effectively and accurately providing geotemperature information essential in estimating the earth’s heat flow; developing the subsidence history including the formation, maturity and migration of hydrocarbon in sedimentary basins, and searching for deep-seated geologic structures favourable to hydrocarbon accumulation.
Keywords: Least-square, Geothermal, Non-Radiogenic, Radiogenic, Crustal Rocks and Niger Delta
Cite this paper: G. I. Alaminiokuma, E. S. Osegbowa, Least-Square Geothermal Models in Crustal Rocks with Non-Radiogenic and Radiogenic Heat Generation Sources in the Niger Delta Basin, Geosciences, Vol. 9 No. 1, 2019, pp. 1-7. doi: 10.5923/j.geo.20190901.01.
Article Outline
1. Introduction
- The present efforts of exploring deeper prospects towards recovering more untapped hydrocarbon in the Niger Delta Basin require accurate data analyses and in-depth knowledge of geotemperature distribution. Temperature distribution in the earth’s subsurface is either of radiogenic source or of formation source or both [1]. Geotemperature distribution in the Continental Crust is governed both by either the conductive heat loss to the surface or heat generated internally by the decay of radioactive isotopes in rocks and heat that flows upward from sub-continental mantle [2]. Several studies have been conducted using the simple gradient method, statistical and geostatistical analyses, thermal resistance method, simple linear increase of temperature with depth among others to determine the geothermal characteristics in different parts of the Niger Delta Basin. A brief review of some of these studies related to geotemperature and its applications and variations are given in Table 1.
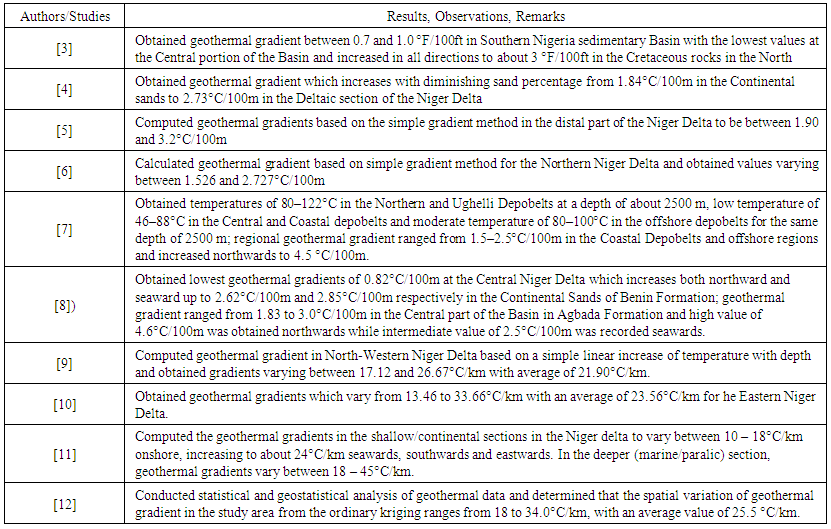 | Table 1. A Review of Studies Related to Geotemperatures |
2. Location and Geology of Niger Delta
- The area of study is the Niger Delta sedimentary Basin (Figure 1). It is situated on the Continental margin of the Gulf of Guinea in Equatorial West Africa between Latitudes 3 °N and 6 °N and Longitude 5 °E and 8 °E.
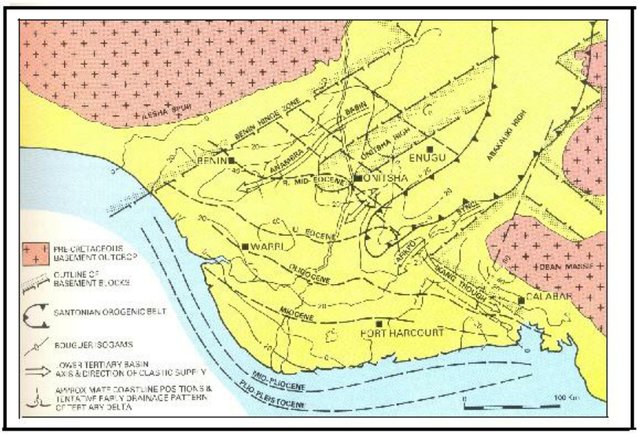 | Figure 1. Map of the Niger Delta Sedimentary Basin |
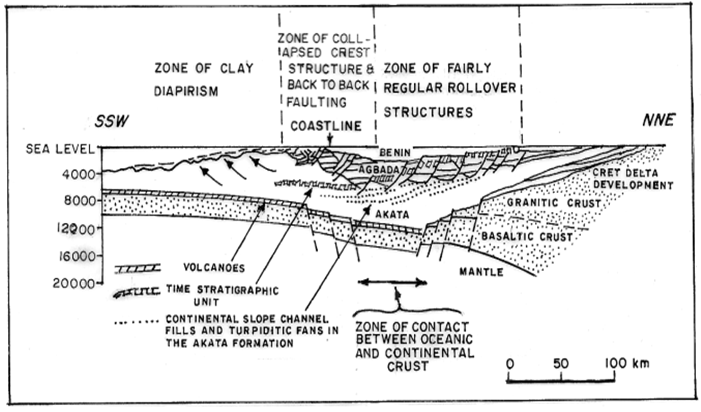 | Figure 2. Map showing the stratigraphy of Niger Delta |
3. Methodology
3.1. Field Data
- Geotemperature data from Continuous Temperature Logs in 26 wells randomly distributed across the Niger Delta Basin were used in this study. These data are reliable since the wells have attained thermal equilibrium after some period of drilling [7].
3.2. Geothermal Model Assumptions
- A homogenous earth model [16] is assumed and the dependence of temperature variation on lithology is neglected so as to observe the variations of temperature with depth ([7]; [17]). The earth is modelled as an isotropic slab to the “Moho” depth of about 36 km to allow for analytic solutions to the Normal equations governing heat conduction problems. The earth’s crust approximates a plane due to its negligible thickness compared with the thickness of the entire earth. This is a 1-layer problem and 1-dimensional heat flow by conduction is assumed due to the solid nature of the earth’s crust.
3.3. Geothermal Model Equations
3.3.1. Non-Radiogenic Heat Generation Case
- For a 1-D steady-state heat conduction through an earth crust that approximates a slab without radiogenic heat generation, external heat penetration and shielded from topographic as well as seasonal changes, the diffusion equations is:
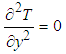 | (1) |
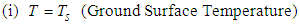 | (2a) |
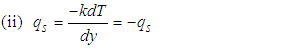 | (2b) |
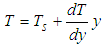 | (3) |
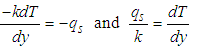 | (4) |
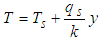 | (5) |
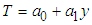 | (6) |
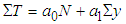 | (7a) |
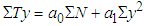 | (7b) |
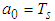 and
and 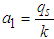 .
. 3.3.2. Radiogenic Heat Generation Case
- If the radiogenic heat (H) is generated per unit volume per unit time, then the heat conduction equation becomes:
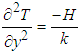 | (8) |
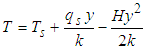 | (9) |
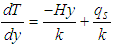 | (10) |
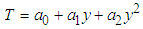 | (11) |
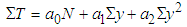 | (12a) |
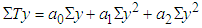 | (12b) |
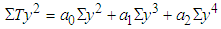 | (12c) |
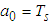 ,
, 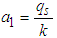 and
and 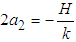 .Solutions to the Normal equations above are obtained by Matrix equations:
.Solutions to the Normal equations above are obtained by Matrix equations: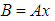 | (13) |
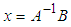 | (14) |
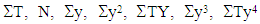 in the Normal equations. Solutions to these equations are obtained by solving the Matrix Algebra using MS Excel package.
in the Normal equations. Solutions to these equations are obtained by solving the Matrix Algebra using MS Excel package.4. Results and Discussion
4.1. Ground Surface Temperature (GST)
- As stated by [18], the ground surface is an important layer which temperature forms an important boundary condition for the determination of geothermal gradient, a parameter which is useful in evaluating the thermal energy resources of any region. Table 2 shows the ground surface temperature (GST) for the 26 wells in this research.
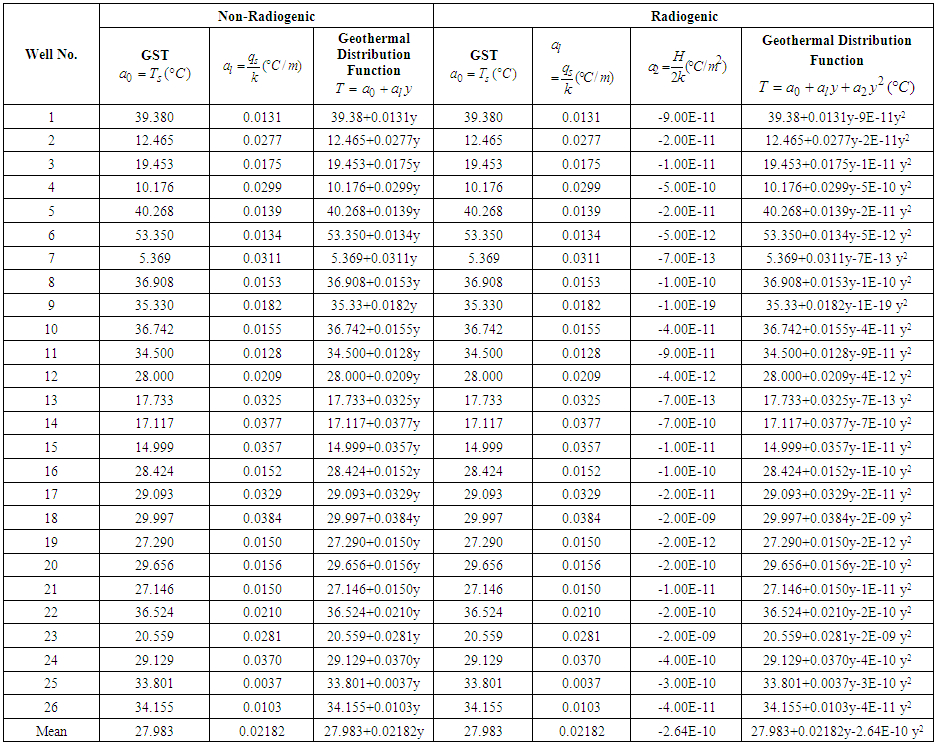 | Table 2. Ground Surface Temperatures (GST) and Least-Square Geothermal Distribution Functions for Crustal Rocks with Non-Radiogenic and Radiogenic Heat Generation for the 26 Wells in the Study Area |
4.2. Geothermal Distribution Functions for Non-Radiogenic and Radiogenic Sources
- Table 2 also shows the geothermal distribution functions for crustal rocks with non-radiogenic and radiogenic heat generation sources for the 26 wells studied. The Least-Square equations indicate linear functions for the non-radiogenic heat generation model and quadratic functions for the radiogenic heat generation model. The mean geotemperature distribution functions for wells 1-26 are computed respectively as:For Non-radiogenic Model:
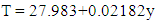 | (15) |
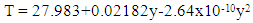 | (16) |
4.3. Geotemperature Gradient of the Niger Delta with Radiogenic Heat Generation
- Table 3 shows the geotemperatures and geothermal gradients for depths extrapolated to the “Moho” in the Niger Delta Basin using the mean geotemperature functions (equations 15 and 16) with Non- Radiogenic and Radiogenic heat generations respectively for wells 1-26.
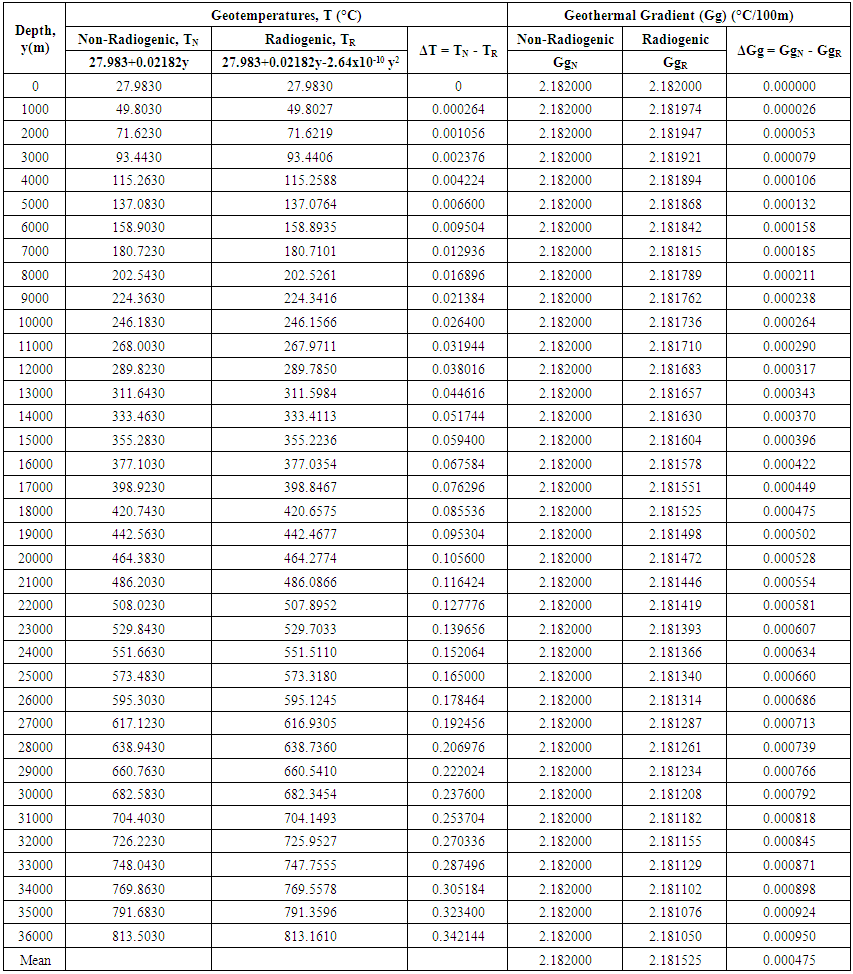 | Table 3. Mean Geotemperatures and Geothermal Gradient Functions to the “Moho” in the Niger Delta Basin |
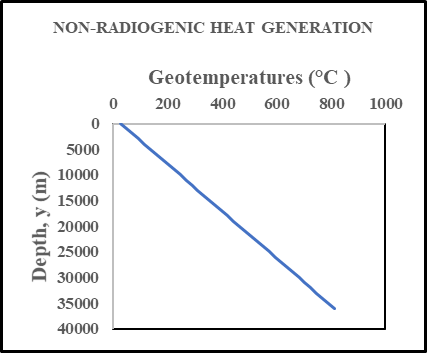 | Figure 3a. Geotemperature (°C) versus Depth (m) for the Non-Radiogenic Heat Generation |
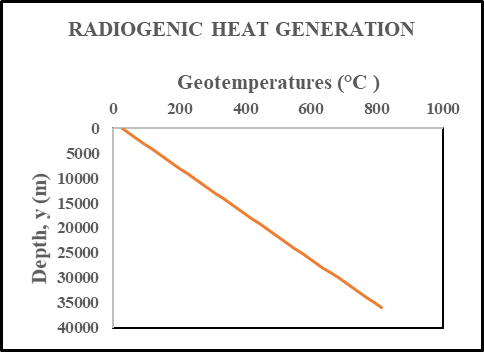 | Figure 3b. Geotemperature (°C) versus Depth (m) for the Radiogenic Heat Generation |
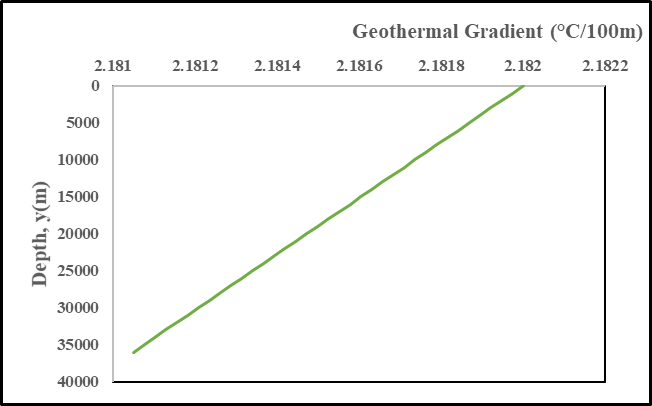 | Figure 4. Geothermal Gradient for the Radiogenic Heat Generation |
5. Conclusions
- The application of the Least Square method for the computations of ground surface temperature, geothermal gradients and generation of geotemperature distribution functions for the non-radiogenic and radiogenic models is suitable for accurate geotemperature analyses since it gives very close results to those of other researchers using different methods in the Niger Delta.The radiogenic heat generation source contributes two significant effects on the subsurface temperature distribution in the region. The low value of radiogenic heat generation per unit thermal conductivity accounts for the small difference between the linear and non-linear Least Square geotemperature model values. The radiogenic model also shows that geotemperature gradient decreases infinitesimally with depth. This can be because of the concentration of radiogenic heat sources with depth based on the stratigraphy in the Niger Delta [13]. The increase in shaliness in the Basin can be viewed as decreasing with depth. This is substantiated by the general trend of decrease in radiogenic heat sources from Crust to the Mantle [1]. It is obvious from the foregoing that the geothermal models of the Niger Delta crust is not significantly affected by the radiogenic heat production of the region.
6. Recommendations
- The geothermal models developed for the Niger Delta Basin crustal rocks considering radiogenic heat generation and employing the Least Squares method provide new frontiers for research in hydrocarbon and geothermal energy resources appraisal in the Basin. A detailed experimental work using Temperature Logs, Gamma Ray Logs (to obtain radiogenic heat generation) and core samples (to determine thermal conductivity) should be conducted in the study area to obtain results for comparison with the approach in this study.Further research should be devoted to the study of the effects of other thermodynamic conditions apart from radiogenic heat generation on geotemperature distribution in the Niger Delta and other sedimentary Basins.
ACKNOWLEDGEMENTS
- The authors wish to thank Shell Petroleum Development Company Nigeria for making available the data used in this research and to the Department of Petroleum Resources for the permission to use the data.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML