| [1] | Arya, A.S., (1992). Possible effects of a major earthquake in Kangra region of Himachal Pradesh, Current Science, 62(1-2), 251-256. |
| [2] | Bock, Y., Prawirodirdjo, L., Genrich, J.F., Stevens, C.W., McCaffrey, R., Subarya, C., Puntodewo, S.S.O., & Calais, E., 2003. Crustal motion in Indonesia from Global Positioning System measurements. Journal of Geophysical Research, 108, 2367. |
| [3] | Chandra, U., (1992). Seismotectonics of Himalaya. Current Science, 62(1-2), 40-71. |
| [4] | Dick, I. D., Proceedings of the 3rd World Conference on Earthquake Engineering, New Zealand, I, 1965, pp. 45–53. |
| [5] | Epstein, B. and Lomnitz, C., A model for the occurrence of large earthquakes. Nature, 1966, 211, 954–956. |
| [6] | Gayskiy, V. N. and Katok, A. P., Primeneniye teorii extremal ''nykh znacheniy dlya ocenki povtoryayemosti sil''nykh zemletryaseniy, sbornik Dinamika zemnoy kory AN SSSR, Nauka, Moskva, 1965, p. 9. |
| [7] | Gumbel, E. J., Statistics of Extremes, Columbia University Press, New York, 1958, p. 375. |
| [8] | Gutenberg, B. and Richter, C. F. (1944). Frequency of earthquakes in California. Bull. Seism. Soc. Am., 34, 185-188. |
| [9] | Hall, R. (1996). Reconstructing Cenozoic SE Asia. In: Hall, R. & Blundell, D. J. (eds). Tectonic Evolution of SE Asia. Ge-ological Society, London, Special Publication, 106, 153-184. |
| [10] | Hall, R. (2011). Australia–SE Asia collision: plate tectonics and crustal flow. In: Hall, R., Cottam M. A., & Wilson M. E. J. (eds). The SE Asian Gateway: History and Tectonics of the Australia– Asia Collision. Geological Society, London, Special Publication, 355, 75–109. |
| [11] | Hamilton, W. (1979). Tectonics of the Indonesian region. U.S. Geological Survey Professional Paper, 1078, 345 pp. |
| [12] | Karnik, V. and Hubernova, Z., The probability of occurrence of largest earthquakes in the European area. Pure Appl. Geophys., 1968, 70, 61–73. |
| [13] | Knopoff, L. and Kagan, Y., Analysis of the theory of extremes as applied to earthquake problems. J. Geophys. Res., 1977, 82, 5647–5657. |
| [14] | Kropotkin, P. N., The problem of continental drift (mobilism). IZV Akad. Nauk., 1969, 3, 139–149. |
| [15] | Lomnitz, C., Global Tectonics and Earthquake Risk, Elsevier, Amsterdam, 1974, p. 320. |
| [16] | Mahajan, A.K., and Kumar, S., (1994). Linear features registered on the Landsat imagery and seismic activity in the Dharmsala-Palampur region (NW Himalaya), Geofizika, 11 (1), 15-25. |
| [17] | Milne, W. G. and Devenport, A. G., Distribution of earthquake risk in Canada. Bull. Seismol. Soc. Am., 1969, 59, 729–754. |
| [18] | Nordquist, J. M., Theory of largest values applied to earthquake magnitudes. Trans. Am. Geophys. Union, 1945, 26-I, 29–39. |
| [19] | Poulos, H. G., (1971). Behavior of laterally loaded piles-I: Single piles. J. Soil Mech. and Found. Div., 97(5), 711–731. |
| [20] | Rangin, Claude, Jolivet, Laurent, Manuel Pubellier, and Tethys Pacific working group (1990). A simple model for the tectonic evolution of southeast Asia and Indonesian region since 43 m.y., Bulletin de la Societe Geologique de France, 8 (6), 889-905. |
| [21] | Reese, L. C., and Matlock, H., (1956). Non-dimensional solu-tions for laterally loaded piles with soil modulus assumed proportional to depth., Proc., 8th Texas Conf. on Soil Me-chanics and Foundation Engineering, Austin, Texas, 1–23 |
| [22] | Reese, L. C., and Welch, R. C., (1975). Lateral loading of deep foundations in stiff clay., J. Geotech. Engrg. Div., 101(7), 633–649. |
| [23] | Shanker, D. and Singh, V. P., Seismic risk analysis for the occurrence of medium size earthquakes in Kangra region of Himachal Pradesh, India. Proc. Indian Natl. Sci. Acad. Part A, 1997, 63, 197–202. |
| [24] | Shanker, D., R.B.S. Yadav and H.N. Singh (2007), “On the seismic risk in the Hindukush-Pamir-Himalaya and their vi-cinity”, Current Sciences, 92 (1), 1625-1630. |
| [25] | Shanker, D., Sherif M. Ali and Manisha Singh, (2017). Earthquake Hazard and Engineering Determinations for Indonesian Region Using IMS Network Data, Geosciences, 7(5): 150-155. |
| [26] | Silver, E.A., Mccaffrey, R., & Smith, R.B. (1983). Collision, rotation and the initiation of subduction in the evolution of Sulawesi, Indonesia. Journal of Geophysical Research, 88, 9407-9418. |
| [27] | Singh, Manisha, D. Shanker and Sherif M. ALI (2015). Seismic Hazard Assessment in Hindukush-Pamir Himalaya Using IMS Network, Geosciences, 5(3): 81-85. |
| [28] | Singh, V. P., Duda, J. and Shanker, D., A plausible model for the present day seismicity and tectonic activity in the Hindukush complex zone. J. Asian Earth Sci., 2005, 25, 147–156. |
| [29] | Spakman, W., & Hall, R. (2010). Surface deformation and slab-mantle interaction during Banda arc subduction rollback. Nature Geoscience, 3, 562-566. |
| [30] | Spencer, J.E., (2011). Gently dipping normal faults identified with Space Shuttle radar topography data in central Sulawesi, Indonesia, and some implications for fault mechanics. Earth and Planetary Science Letters, 308, 267-276. |
| [31] | Valdiya, K.S., (1976). Himalayan transverse faults and folds and their parallelism with subsurface structures of noth Indian Plains; Tectonophysics, 32, 353-386. |
| [32] | Valdiya, K.S. Rana, R.S. and Sharma, P.K., (1992). Active Himalayan Frontal fault, Main Boundary Thrust and Ramgarh Thrust in Southern Kumaun; Jour. Geol. Soc. India, 40, 509-528. |


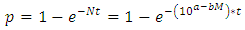
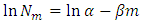
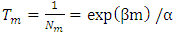
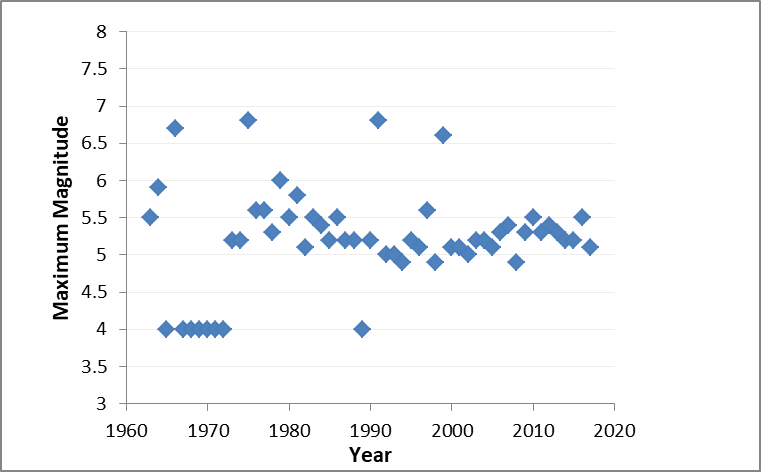
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML