-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Geosciences
p-ISSN: 2163-1697 e-ISSN: 2163-1719
2013; 3(2): 60-67
doi:10.5923/j.geo.20130302.04
Aseismic Ground Deformation in a Viscoelastic Layer over Lying a Viscoelastic Half-Space Model of the lithosphere-Asthenosphere System
Subrata Kr. Debnath1, Sanjay Sen.2
1Department of Basic Science and Humanities, Meghnad Saha Institute of Technology (A unit of Techno India Group), Nazirabad.P.O. Uchhepota, Via- Sonarpur, Kolkata, 700150, India
2Department of Applied Mathematics, University of Calcutta, 92, APC Road, Kolkata 700009, India
Correspondence to: Subrata Kr. Debnath, Department of Basic Science and Humanities, Meghnad Saha Institute of Technology (A unit of Techno India Group), Nazirabad.P.O. Uchhepota, Via- Sonarpur, Kolkata, 700150, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The process of stress −accumulation near earthquake faults during the aseismic period in between two major seismic events in seismically active regions has become a subject of research during the last few decades. A long strike-slip fault in a viscoelastic layer over a viscoelastic half space representing the lithosphere-asthenosphere system has been considered here. Stresses accumulate in the region due to various tectonic processes, such as mantle convection and plate movements etc, which ultimately leads to movements across the fault. In the present paper, a two-dimensional model of the system is considered and expressions for displacements, stresses and strains in the model have been obtained using suitable mathematical techniques developed for this purpose. A detailed study of these expressions may give some ideas about the nature of stress accumulation in the system, which in turn will be helpful in formulating an effective earthquake prediction programme.
Keywords: Viscoelastic Layered Model, Aseismic Period, Stress Accumulation, Mantle Convection, Plate Movements, Tectonic Process, And Earthquake Prediction
Cite this paper: Subrata Kr. Debnath, Sanjay Sen., Aseismic Ground Deformation in a Viscoelastic Layer over Lying a Viscoelastic Half-Space Model of the lithosphere-Asthenosphere System, Geosciences, Vol. 3 No. 2, 2013, pp. 60-67. doi: 10.5923/j.geo.20130302.04.
Article Outline
1. Introduction
- Modeling of dynamic processes leading to an earthquake is one of the main concerns of seismologist. Two consecutive seismic events in a seismically active region are usually separated by a long aseismic period during which slow and continuous aseismic surface movements are observed with the help of sophisticated measuring instruments. Such aseismic surface movements indicate that slow aseismic change of stress and strain are occurring in the region which may eventually lead to sudden or creeping movements across the seismic faults situated in the region.It is therefore seems to be an essential feature to identify the nature of the stress and strain accumulation in the vicinity of seismic faults situated in the region by studying the observed ground deformations during the aseismic period. A proper understanding of the mechanism of such aseismic quasi static deformation may give us some precursory information regarding the impending earthquakes.A pioneering work involving static ground deformation in elastic media were initiated by ([8], [9]), ([21]), ([2]), ([3]),([6]), ([23]). Reference ([22]) has discussed various aspects of fault movement in his book. Reference ([5]) has discussed stress accumulation near buried fault in lithosphere-asthenosphere system. In most of these studies the medium were taken to be elastic and /or viscoelastic, layered or otherwise. We now focus on some of the reasons of consideration of viscoelastic layer over viscoelastic half space model.The laboratory experiments on rocks at high temperature and pressure indicates the imperfect elastic behavior of the rocks situated in the lower lithosphere and asthenosphere.Investigations on the post-glacial uplift of Fennoscandia and parts of Canada indicate that at the termination of the last ice age, which happened about 10 millennia ago a 3km. ice cover melted gradually leading to upliftment of the regions .Evidence of this upliftment has been discussed in Fairbridge (1961), Schofield (1964), Chathles (1975), if the Earth were perfectly elastic, this deformation would be managed after the removal of the load, but it did not happened, indicating that the Earth crust and upper mantle is not perfect elastic but rather viscoelastic in nature.Therefore in the present case we consider a long strike-slip fault situated in a viscoelastic layer over a viscoelastic half -space which is surface breaking in nature. The medium is under the influence of tectonic forces due to mantle convection or some related phenomena. The fault undergoes a creeping movement when the stresses in the region exceed certain threshold values.
2. Formulation
- We consider a long strike-slip fault F width D situated in a viscoelastic layer over a viscoelastic half space of linear Maxwell type.We choose our rectangular Cartesian coordinates (y1, y2, y3) such that, the free surface is the plane y3 = 0 the fault F1 is in the plane y2 = 0, y1-axis is perpendicular to plane of the fault and y3 axis pointing downwards as shown in the Fig: 1.Since our model is a viscoelastic layer of finite depth say H, over a viscoelastic half space.∴ The interface is the plane y3 = H.We consider the fault F1 in the region y2 = 0, 0 < y3 < D1 < H The half space is y3 > H.
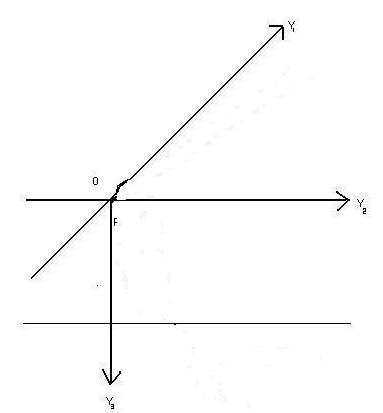 | Figure 1. Section of the model by the plane y1=0 |
2.1. Constitutive Equations
- For perfect elastic body we know as soon as the stress is removed. The strain also disappears but for viscoelastic body, the strain does not at once remove.To incorporate the viscoelastic effects stress-strain relations of a slightly different form have been suggested.We have the constitutive equations (i.e., stress -strain relation) as, for the layer M1,
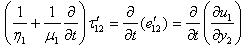 | (1.1) |
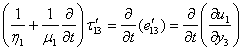 | (1.2) |
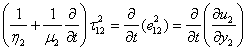 | (1.3) |
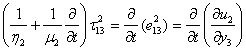 | (1.4) |
2.2. Stress Equation of Motion
- We have the stress equation of motion as
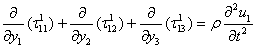 Since displacement, stress and strain are independent of y1 therefore the stress equation becomes,
Since displacement, stress and strain are independent of y1 therefore the stress equation becomes,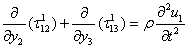 ,ρ= average density of M1Since our observation is in the aseismic period while the order of displacement is 10−4 c.g.s. unit or less.∴ The inertial term
,ρ= average density of M1Since our observation is in the aseismic period while the order of displacement is 10−4 c.g.s. unit or less.∴ The inertial term 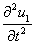 is extremely small. Therefore, we neglect it. Stress equation of motion for the layer M1 is
is extremely small. Therefore, we neglect it. Stress equation of motion for the layer M1 is 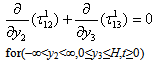 | (1.5) |
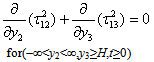 | (1.6) |
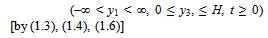 | (1.7) |
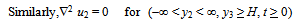 | (1.8) |
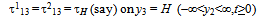 | (1.9) |
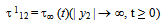 | (1.10), |
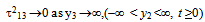 | (1.11) |
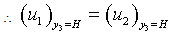 | (1.11.1) |
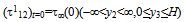 | (1.12) |
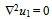 | (1.13) |
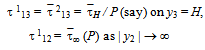 | (1.14) |
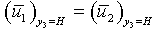 | (1.15) |
3. Solutions in Absence of Fault Creep ([24], [25])
- Solving the boundary value problem, (1.12)-(1.15)We get,
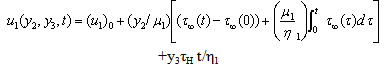 | (2.1) |
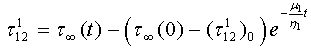 | (2.1.1) |
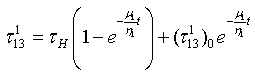 | (2.1.2) |
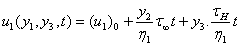 | (2.2) |
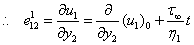 | (2.3) |
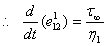 | (2.4) |
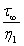 = 2x10−13 /sec = 6 x 10−6 / year which tally with the observational value which is order 10−6 to 10−7.
= 2x10−13 /sec = 6 x 10−6 / year which tally with the observational value which is order 10−6 to 10−7.4. Displacements and Stresses after the Commencement of Fault Creep across the Fault F1:([24],[25])
- In our paper we are considering 1 creeping fault in the layer M1. If the creep commences across F at time t = T1, then the relations (1.1) to (1.10) are satisfied and we have the following creeping conditions.
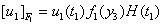 | (3.1) |
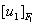 is the discontinuity in the displacement u1 across the fault F1.
is the discontinuity in the displacement u1 across the fault F1.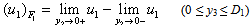 | (3.1.2) |
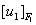 = 0 for t1 < 0 and H (t1) Heaviside unit step function.∴ The velocity of the creep is
= 0 for t1 < 0 and H (t1) Heaviside unit step function.∴ The velocity of the creep is 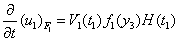 where
where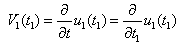 Taking Laplace transformation of (3.1)
Taking Laplace transformation of (3.1)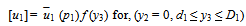 | (3.2) |
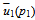 is the Laplace transformation of u1 (t1) with respect to t1 and is given by
is the Laplace transformation of u1 (t1) with respect to t1 and is given by 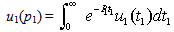 Now we try to find u1, τ121, τ131 in the form,
Now we try to find u1, τ121, τ131 in the form,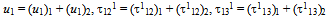 | (3.3) |
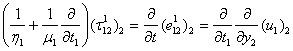 | (3.4) |
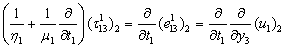 | (3.5) |
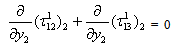 | (3.6) |
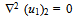 | (3.7) |
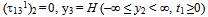 | (3.8) |
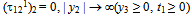 | (3.9) |
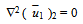 | (3.10), |
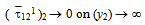 | (3.11) |
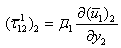 | (3.12) |
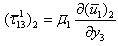 | (3.13) |
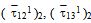 , finally, inverse Laplace Transform of which will give (u1)2 (τ121)2, (τ131)2.Now let Q (y1, y2, y3) be any point in the M1 and P (x, x2, x3) be any point on F1. The by ([9]),
, finally, inverse Laplace Transform of which will give (u1)2 (τ121)2, (τ131)2.Now let Q (y1, y2, y3) be any point in the M1 and P (x, x2, x3) be any point on F1. The by ([9]),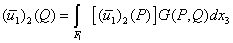 | (3.14) |
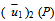 is the discontinuity in
is the discontinuity in 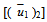 across F1 and is given by
across F1 and is given by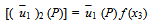 where P= Laplace transformation variable.Therefore, from we get,
where P= Laplace transformation variable.Therefore, from we get,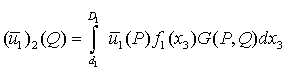 | (3.15) |
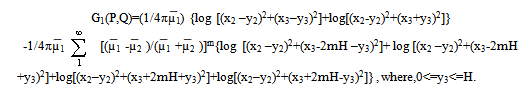 | (3.16) |
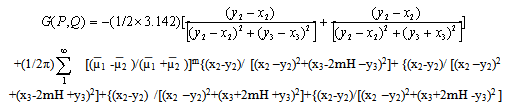 | (3.17) |
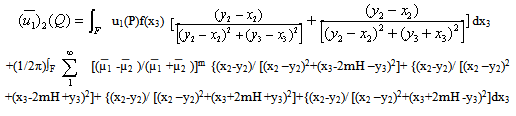 | (3.18) |
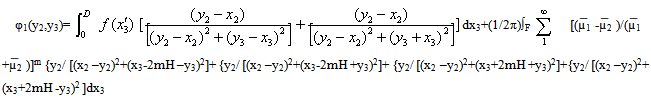
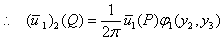 | (3.19) |
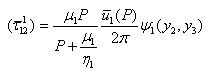
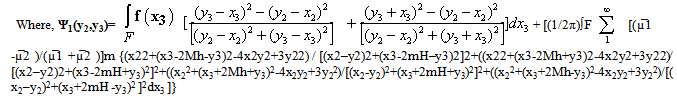 On the fault F1, x2 = 0
On the fault F1, x2 = 0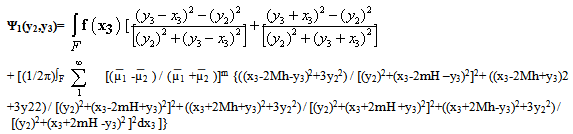 | (3.21) |
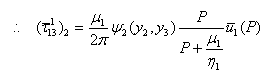 | (3.22) |
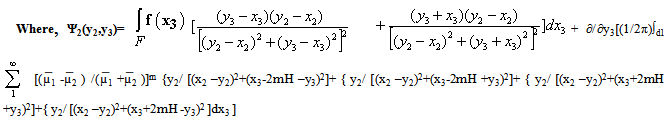 On the fault ,x2 = 0
On the fault ,x2 = 0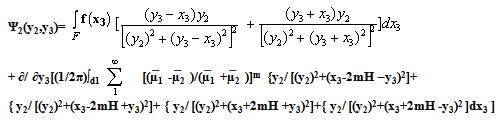 | (3.23) |
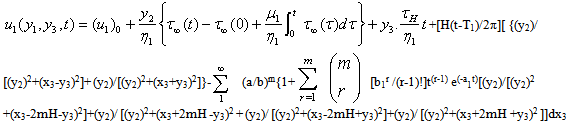 | (3.24) |
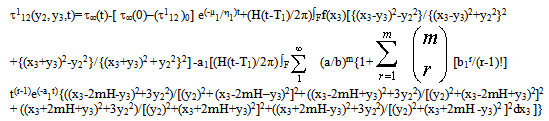 | (3.25) |
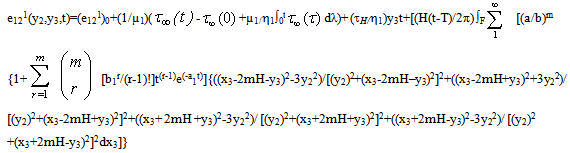 | (3.26) |
5. Numerical Computations
- Following [1] and recent studies on rheological behavior of crust and upper mantle by ([4], [7]) the values of the model parameters are taken as :µ1=3.1011dynes/cm2,µ2=2.1011 dynes/cm2 ,η1= 2.1021 poise and η2=3. 1021 poise . D1 = Depth of the fault = 40 km., [nothing that the depth of all major earthquake faults is in between 10-35 km].
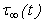 =constant=
=constant= 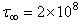 dynes/cm2 (200 bars), [post seismic observations reveal that in most of the cases, stress released in major earthquake are of the order of 200 bars or less, in extreme cases, it may be 400 bars.]
dynes/cm2 (200 bars), [post seismic observations reveal that in most of the cases, stress released in major earthquake are of the order of 200 bars or less, in extreme cases, it may be 400 bars.]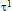 12(y2,y3,0)= 5x107dyne/cm2 (50 bars),and
12(y2,y3,0)= 5x107dyne/cm2 (50 bars),and 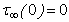 We take the creep function,
We take the creep function, 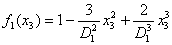 ,with U=1cm/year, satisfying the conditions stated in
,with U=1cm/year, satisfying the conditions stated in 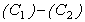 .The rate of change of shear strain is:∂/∂t(e121)=1/η1+(τH/η1)y3+[(H(t-T)/2π)∫F
.The rate of change of shear strain is:∂/∂t(e121)=1/η1+(τH/η1)y3+[(H(t-T)/2π)∫F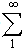 [(a/b)m{1+
[(a/b)m{1+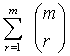 [b1r/(r-1)!][-a1t(r-1)e(-a1t)+(r-1)tr-2e(-a1t)]{((x3-2mH-y3)2-3y22)/[(y2)2+(x3-2mH–y3)2]2+((x3-2mH+y3)2+3y22)/[(y2)2+(x3-2mH+y3)2]2+((x3+2mH+y3)2-3y22)/[(y2)2+(x3+2mH+y3)2]2+((x3+2mH-y3)2-3y22)/ [(y2)2+(x3+2mH-y3)2]2dx3]} (3.27) The rate of shear stress12 is: [∂τ112(y2, y3,t)/∂t]= -(µ1/η1) [ τ∞(0) –(τ112)0]e-(µ1/η1)t +[(H(t-T1)/2π)∫F
[b1r/(r-1)!][-a1t(r-1)e(-a1t)+(r-1)tr-2e(-a1t)]{((x3-2mH-y3)2-3y22)/[(y2)2+(x3-2mH–y3)2]2+((x3-2mH+y3)2+3y22)/[(y2)2+(x3-2mH+y3)2]2+((x3+2mH+y3)2-3y22)/[(y2)2+(x3+2mH+y3)2]2+((x3+2mH-y3)2-3y22)/ [(y2)2+(x3+2mH-y3)2]2dx3]} (3.27) The rate of shear stress12 is: [∂τ112(y2, y3,t)/∂t]= -(µ1/η1) [ τ∞(0) –(τ112)0]e-(µ1/η1)t +[(H(t-T1)/2π)∫F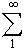 (a/b)m{1+
(a/b)m{1+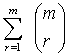 [b1r/(r-1)!][- a1t(r-1) e(-a1t) +(r-1)tr-2 e(-a1t)]{((x3-2mH-y3)2+3y22) / [(y2)2+(x3-2mH –y3)2]2+ ((x3-2mH+y3)2 +3y22) / [(y2)2+(x3-2mH +y3)2]2+ ((x3+2mH+y3)2+3y22) / [(y2)2+(x3+2mH +y3)2]2+((x3+2mH-y3)2+3y22)/[(y2)2+(x3+2mH-y3)2]2dx3]} (3.28)
[b1r/(r-1)!][- a1t(r-1) e(-a1t) +(r-1)tr-2 e(-a1t)]{((x3-2mH-y3)2+3y22) / [(y2)2+(x3-2mH –y3)2]2+ ((x3-2mH+y3)2 +3y22) / [(y2)2+(x3-2mH +y3)2]2+ ((x3+2mH+y3)2+3y22) / [(y2)2+(x3+2mH +y3)2]2+((x3+2mH-y3)2+3y22)/[(y2)2+(x3+2mH-y3)2]2dx3]} (3.28) 6. Discussions and Conclusions
- (A) Variation of displacement due to the creep movement across the fault after t1=1year.Equation (3.24) gives the displacement U1 at any point (y2,y3) at any time t, due to the fault movement across the fault F. Fig 2 shows the variation of displacement U1 with depth y3 for y2=8km. t=1year.It is observed that maximum displacement occurred at y3=0 and it’s magnitude is 2.25 cm/year and it gradually decreases to zero at a depth about 100km from the free surface.
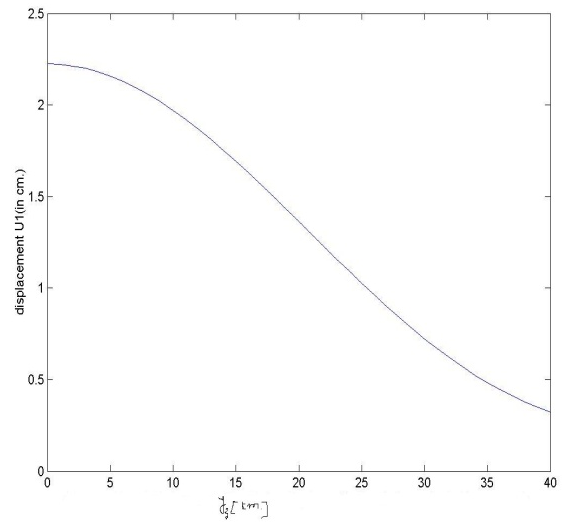 | Figure 2. shows the variation of displacement U1 with depth y3 for y2=8km. t1=1year due to fault movement |
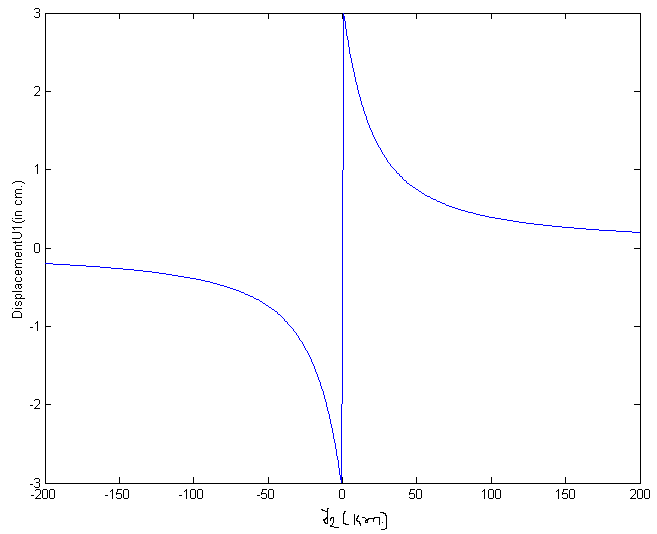 | Figure 3. shows the variation of surface displacement U1 for y3=0km.and t1=1year with y2 due to the fault movement across the fault F |
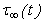 /η1 which represents a straight line through the origin with slope <<1.
/η1 which represents a straight line through the origin with slope <<1.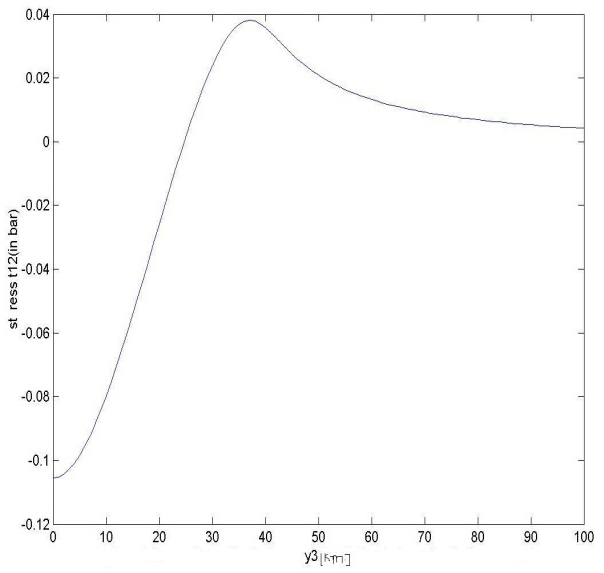 | Figure 4. shows the variation of stress t12 with y3 for y2=5km.t1=1year due to the fault movement across the fault F |
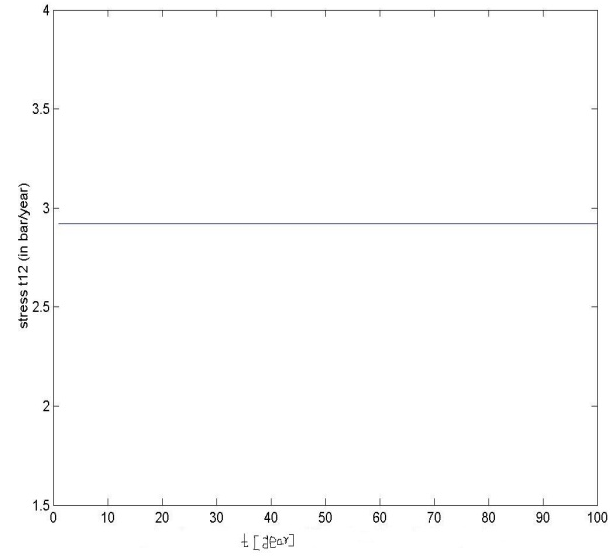 | Figure 5. variation of shear stress t12 with time ‘t’ for y2=5km. y3=10km |
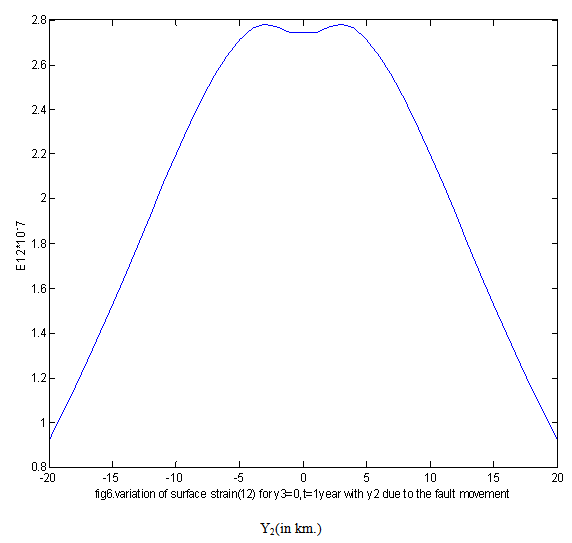 | Figure 6. variation of surface shear strain E12 for t1=1 year, with y2 for y3=0km.due to the fault movement |
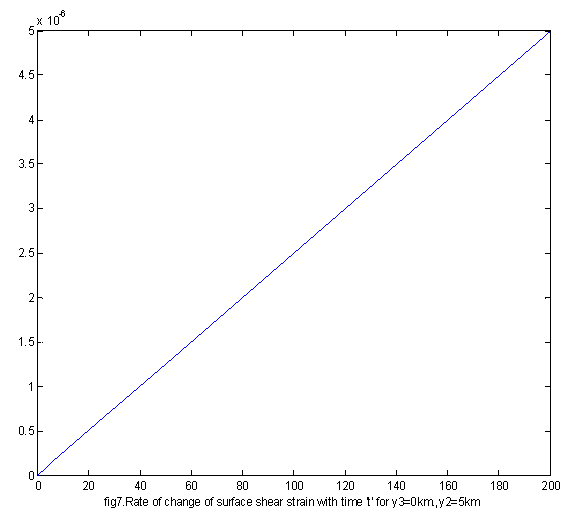 | Figure 7. Rate of change of surface shear strain e 12 for y3=0,y2=5km |
ACKNOWLEDGEMENTS
- One of the authors (Subrata Kr. Debnath) thanks the Principal and Head of the Department of Basic Science and Humanities, Meghnad Saha Institute of Technology, a unit of Techno India Group(INDIA),for allowing me to pursue the Ph.D.thesis, and also thanks the Geological Survey of India, Kolkata, ISI Kolkata, for providing me the library facilities.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML