-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Geosciences
p-ISSN: 2163-1697 e-ISSN: 2163-1719
2012; 2(3): 39-50
doi: 10.5923/j.geo.20120203.02
Trend Prediction of Seismicity in Lower Reaches of Yangtze River – Yellow Sea (Y-Y) Seismic Belt in 2011-2020
1Shanghai Earthquake Administration, Shanghai, 200062, China
2Department of Mechanical Engineering University of Louisiana, Lafayette, LA70504, USA
Correspondence to: Wenlong Liu , Shanghai Earthquake Administration, Shanghai, 200062, China.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this study, seismic activity trend of lower reaches of Yangtze River – Yellow Sea (Y-Y) seismic belt during 2011-2020 is predicted based on statistic analysis of historical earthquake data and seismic activity analysis of recent mid-strong earthquakes occurred in this area. Three potential seismic risk zones are indicated where the destructive earthquakes might occur which will cause damages in that area. The three zones and the estimated magnitudes of potential earthquakes are: 1) southern sags of Southern Yellow sea and coastal regions, Ms ≥ 6; 2) Yangtze estuary and its eastern sea area, Ms ≥ 5; 3) areas along Changshu city to Taicang city, Ms ≥ 5. Seismic parametric study of that area is performed to support our conclusions.
Keywords: Seismic Activity, Yangtze River – Yellow Sea Seismic Belt, Trend Prediction, Parametric Study, Potential Risk Zones
Article Outline
1. Introduction
- Major tasks of the analysis of seismicity trend include determine the current phase of the seismicity in studied seismic zones and belts, roughly estimate future seismicity level in those areas, and predict the locations in which strong seismic activities may occur. In general earthquake prediction, the objective of seismicity analysis trend is to correctly describe the time, location, and intensity of the future earthquakes. The prediction opinion will be made based on the possibility that most likely to occur. This study investigated the comparison of historical seismic activity staging, multiple mathematical statistics models, and recent seismicity in Shanghai and its vicinity, etc. The final predictions are made based on these investigation as well as the analysis of medium’s Q value and other seismic source dynamics parameters The seismic zone from lower reaches of Yangtze River to southern Yellow Sea is chosen as the study area and our analysis results will be compared to the previous data.
2. Analysis Method
- Several methods are being used for seismicity trend analysis. One method is to compare characteristics of seismic active period, include the lasting time duration, seismicity level (number of strong earthquakes, total released energy, etc.), and evolution characteristics of the seismicity process, etc; and predict the characteristics of future seismicity in the current seismic active period based on the comparison results. However, due to the limit of historic seismic data and the complexity of seismic process, features of different active period may show some repeatability but usually render distinct differences.Another method is to apply seismic related and triggering factors in different seismic zones and belts. For example, the changing of the Earth’s rotation speed and sunspot activity level may induce the seismic activity. Fig. 1 clearly shows that the seismicity in China synchronizes with the global seismicity. Therefore the seismicity in mainland of China can be inferred from the global seismicity. Fig. 2 explains that when the Earth rotates faster, the activity of shallow earthquakes in North China-Northeast Plain usually decreases, while the seismicity in the regions of Liupan mountain-Qilian mountain-Altyn mountain increases, and vice versa. Thus, the seismicity level in those areas can be predicted from the variation of the Earth’s rotation speed. The third method is based on characteristic analysis of the curves of released strain energy in seismic areas. The released strain energy curves can be classified to three types. (1) Linear type with stable slope, the corresponding seismic areas have comparatively high seismicity level, where strong earthquakes occur frequently with regular time interval. The maximum earthquake magnitude can be extrapolated from the curve (as shown in Fig. 3). (2) The curve with increasing slope, which indicates a high level of accumulated strain energy in corresponding seismic areas thereby indicating strong seismic activities in the future (Fig. 4). (3) The curve with decreasing slope, from which it can be deduced that the future seismicity level will not be too high in the corresponding seismic areas (Fig. 5).
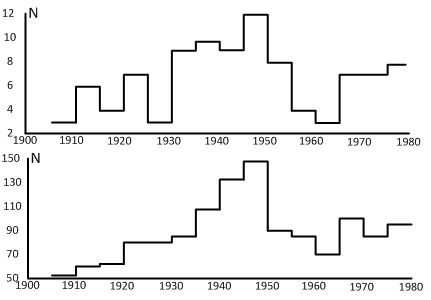 | Figure 1. Frequentness of earthquakes in global and mainland of China (a) Ms ≥ 63/4 shallow earthquakes in mainland of China (b) global earthquakes with Ms≥ 7 |
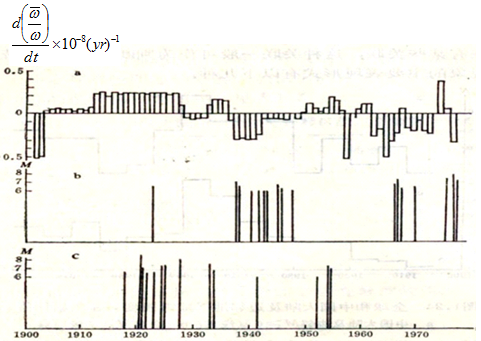 | Figure 2. (a) Rate of change of the Earth’s rotation angular speed (b) shallow earthquake in North China-Northeast Plain (c) earthquakes in Liupan-Qilian-Altyn |
 | Figure 3. Curve of released strain energy in Taiwan seismic zone |
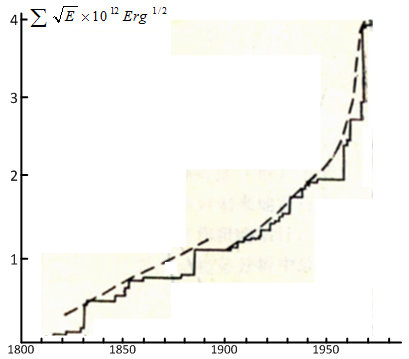 | Figure 4. Curve of released strain energy in North China seismic subzone |
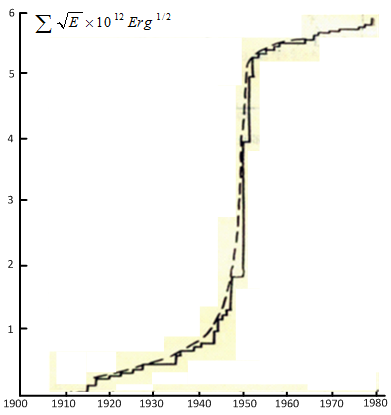 | Figure 5. Curve of released strain energy in South Tibet seismic belt |
3. Working Procedure
- (1) Select appropriate area for study. In this step, we need to select an entire seismic active area, neither choose part of that area nor mix one seismic active area with another. If the selected area is not appropriate for seismic study, it will be difficult to obtain regular historic statistical law from the study, therefore fail to provide meaningful historic data for seismicity trend analysis.(2) Investigate the seismicity in different seismic periods by making diagrams of M-t,
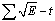 , and N-t. Plot the distribution of epicenter in different seismic periods to study the spatial evolving process of the seismic activity. Important factors that affect the spatial evolving process include: (a) if those seismic periods appeared regularly, the duration of each seismic period, their seismicity level, and similarities and differences among the seismic activities in different periods; (b) characteristics of the spatial distribution of different seismic periods; (c) correlations (especially the sequential relationship) among seismic activities in different seismic zones and belts, and epicenter migration; (d) effects of some environmental factors (rotation of the Earth, sunspot, tides, etc.).(3) Determine the current stage of the seismic activities and predict the future seismicity level. For example, the seismicity in a seismic zone will be in active period in the near future if one of following conditions is satisfied. (a) The seismicity is in an active period and its lasting time is shorter than the shortest active period in history; (b) it is in a quiet period but its lasting time is close to the longest quiet period in history; or (c) the strain release curve accelerates. (4) Determine and predict the intensity of seismic activity using extrapolation of the strain release curve or the data obtained from mathematical statistics. (5) Roughly estimate the risk zones of strong earthquakes, major seismic active areas in current stage, epicenter migration, immunity zones of strong earthquakes, and intervals of time in which strong earthquakes occur.Fig.6 displays the flowchart of trend analysis of seismicity.
, and N-t. Plot the distribution of epicenter in different seismic periods to study the spatial evolving process of the seismic activity. Important factors that affect the spatial evolving process include: (a) if those seismic periods appeared regularly, the duration of each seismic period, their seismicity level, and similarities and differences among the seismic activities in different periods; (b) characteristics of the spatial distribution of different seismic periods; (c) correlations (especially the sequential relationship) among seismic activities in different seismic zones and belts, and epicenter migration; (d) effects of some environmental factors (rotation of the Earth, sunspot, tides, etc.).(3) Determine the current stage of the seismic activities and predict the future seismicity level. For example, the seismicity in a seismic zone will be in active period in the near future if one of following conditions is satisfied. (a) The seismicity is in an active period and its lasting time is shorter than the shortest active period in history; (b) it is in a quiet period but its lasting time is close to the longest quiet period in history; or (c) the strain release curve accelerates. (4) Determine and predict the intensity of seismic activity using extrapolation of the strain release curve or the data obtained from mathematical statistics. (5) Roughly estimate the risk zones of strong earthquakes, major seismic active areas in current stage, epicenter migration, immunity zones of strong earthquakes, and intervals of time in which strong earthquakes occur.Fig.6 displays the flowchart of trend analysis of seismicity. | Figure 6. Flowchart of trend analysis of seismicity |
4. Seismicity Trend in Interested Areas
4.1. Data
- The study area of this research, the seismic zone from lower reaches of YangtzeRiver to southern Yellow Sea, includes two areas: Eastern China (29º-37º N, 100º-124º E) and Shanghai and its vicinity (29º-34º N, 118º-124º E). All the historical seismic data of these two areas used for this study come from local historical records (for earthquakes occurred before 20th century) and seismic data recorded by local observatories (for earthquakes occurred since 20th century, especially since last 70’s) [1-3]. Lee et al. [4] studied the conserving probability of seismic data in Eastern China based on completeness of the historical records and obtained the conserving probabilities of Eastern Chinese seismic data in different centuries (Table 1). From Table 1, it can be found that a complete historical catalog (with probability close to 1) of Eastern Chinese earthquakes is only available after 15th or 16th century (after 1400 or 1500), which can be used for statistical analysis.Based on all available historical seismic data, it can be concluded that: (1) historical records for earthquakes occurred in that area before 1491 are seriously missed. (2) From 1491 till 1900, the records for land and coastal earthquakes with Ms ≥ 5.0 are fairly complete, but most sea earthquakes were not recorded except four sea earthquakes with Ms ≥ 6.7. (3) Since 1905, with application of modern monitoring instruments, a complete seismic data of all the earthquakes with Ms ≥ 5.0 in this area becomes available. Hence, in this research we investigate the seismic data of earthquakes with Ms ≥ 5.0 which occurred after 1491 and especially focus on those occurred since 1905.
4.2. Comparison of Active Periods
- Following figures and tables compare the characteristics of earthquakes occurred in the Y-Y seismic zone during different episodes since 1491.
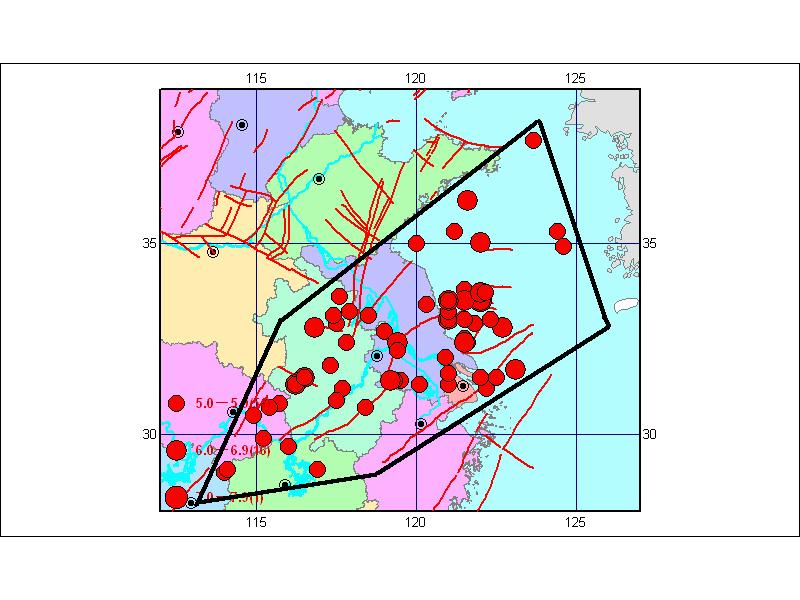 | Figure 7. Distribution of epicenters of earthquakes in Y-Y zone (1491-1998, Ms ≥ 5) |
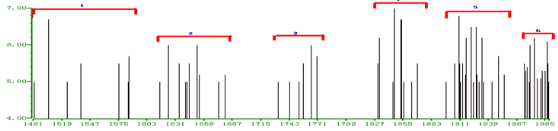 | Figure 8. M-T plot for historical earthquakes in Y-Y zone (1491-1998) |
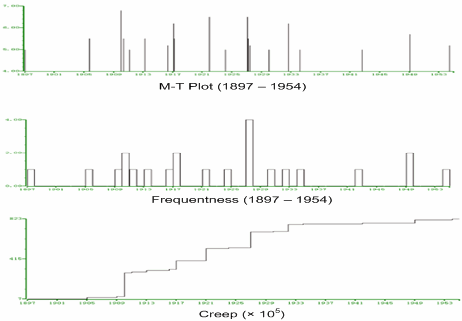 | Figure 9. M-T, N-T, and -T plots for earthquakes in the fifth episode (1897-1954). -T plots for earthquakes in the fifth episode (1897-1954). |
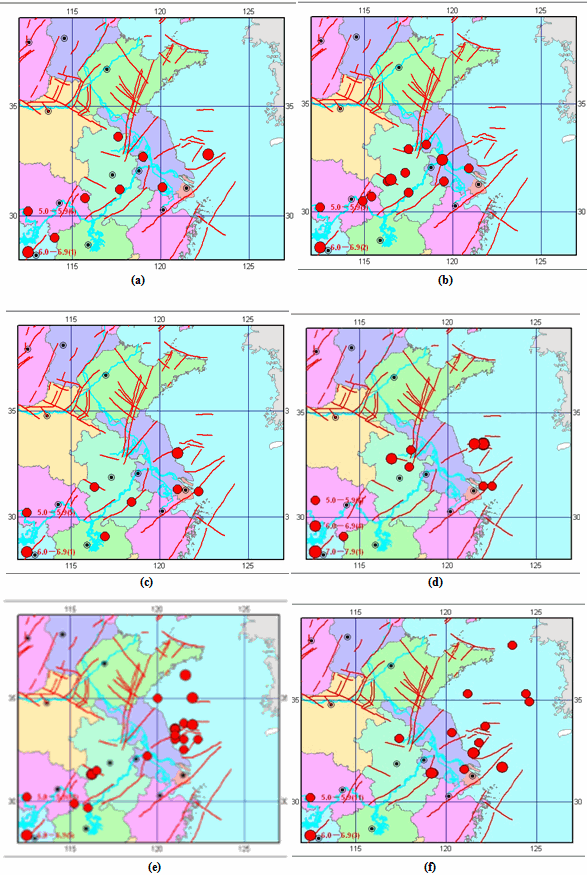 | Figure 10. Distribution of epicenters of earthquakes in (a) 1st episode (1491-1585) (b) 2nd episode (1615-1679) (c) 3rd episode (1731-1770) (d) 4th episode (1829-1868) (e) 5th episode (1897-1954) (f) 6th episode (1974-?). |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.3. Statistical Forecast of Seismicity in Subareas
- Next, we divided the Y-Y belt into three subzones (north, central, and south) and the intensity of seismicity in the decades to come in those subzones were estimated using statistical forecast.
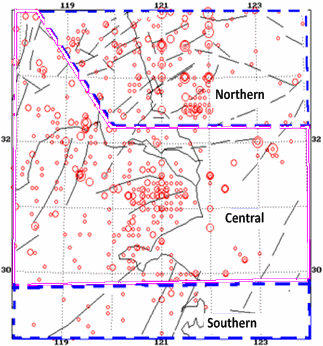 | Figure 11. Distribution of earthquakes in Shanghai and its vicinity, as well as northern, central, and southern parts of this area |
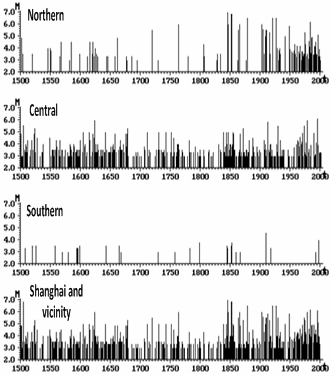 | Figure 12. M-T plots for earthquakes in Shanghai and its vicinity, as well as northern, central, and southern parts of this area |
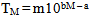 | (1) |
|
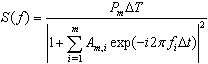 | (2) |
|
|
5. Medium’s Q Value and Stress Drop of Partial Small-Medium Earthquakes in Y-Y Seismic Belt
5.1. Studied Area and Data
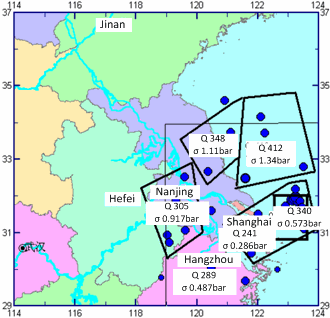
- In order to reveal the relationship among earthquake magnitude, Q value, and stress drop of small earthquakes, the study area (29º~34ºN, 119º~124ºE) is divided into five small regions based on distributions of potential hypocentral regions and earthquakes so that each region possesses a certain amount of records of earthquake data (Fig. 13). Average Q value and stress drop Δσ are calculated for each region. Specifically, since the Ms6.1 occurred in Nov-9-1996 at (32ºN, 123ºE) had a evident influence on Shanghai are, the current Q values and Δσ are calculated as well as the then values before and right after that earthquake.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
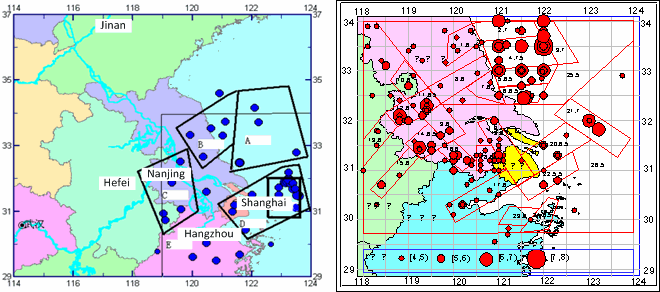 | Figure 13. Partitioning of study area (a) five regions (b) potential hypocentralretions |
5.2. Methods and Data Processing
- Solve medium’s average Q valuesAssume n earthquakes are recorded by an observatory within the same area and spectrum of the ith earthquake is:
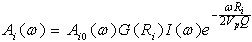 | (3) |
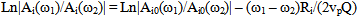 | (4) |
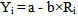 | (5) |
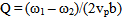 | (6) |
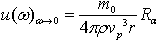 | (7) |
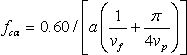 | (8) |
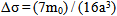 | (9) |
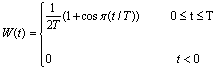 | (10) |
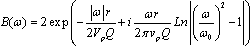 | (11) |
5.3. Summary
- The solved results are displayed in Fig. 14 and Table 8. The relative errors of spectral curves caused from digitalization are about 1~ 2% [12] and the errors of the Q values are in the same magnitude. Thus, the presented differences among the average Q values of different regions are meaningful. The most important factor that causes errors in stress values is the error of earthquake magnitude, whose maximum acceptable value is 0.3. The maximum relative error of stress τ0 can reach 70% [12]. Since the average stress value of each region is a result of multiple earthquakes, it can be considered that the average stress drops in regions A, B, and C are comparatively higher, next are the stress drops in regions E and F, and the stress drop in region D is the lowest. From the calculation results, it is observed that the highest average Q value appears in region A’s sea area, which is 412. Other high Q values include 348 which appears in the central Jiangsu Province and coastal area of region B; 340 which appears in region F (close to the epicenter of the Nov-9-1996 earthquake); and 305 which appears in Liyang of region C. The lowest average Q value appear in Shanghai and the sea area to the east of Hangzhou Bay (in region D), which is 241. And the Q values in other regions are 289. Comparing the distribution of Q values to the potential seismic source areas, it shows that the higher Q values appear in the potential source areas of higher-magnitude earthquakes. This is because that only under a high Q value, the medium can accumulate high-level stress therefore gives rise to strong earthquakes. The Q value in region F dropped from 352 to 342 after the Ms6.1 earthquake occurred in Nov-9-1996 on estuary of Yangtze River. Normally, the Q value will drop after the mid-strong earthquakes because of destruction of local medium. Considering measurement errors, the decrease in Q value after that Ms6.1 earthquake is slight, which indicates that the damage caused by the Ms6.1 earthquake in the local medium was small. The current Q value in that area is 340, which is the same as the one right after the Ms6.1 earthquake. From distribution of the stress drop Δσ, it is found that the drop is high in regions A, B, C, and the next high Δσ appears in regions E and F. The stress drop in region D is comparatively low. From time evolution, it seems that the period of high stress drop corresponds to the time period of high seismicity level in that region.Based on above discussion, it should be noted the possibility of about Ms6.0 earthquakes in the Southern Yellow Sea and coastal area (regions A and B), the sea area to the east of Yangtze estuary (region F) and Liyang and vicinity (region C).
|
6. Conclusions
- The conclusions made based on the earthquake prediction can be listed as:(1) Historical earthquakes occurred in the Y-Y seismic zone can be classified into six episodes and each episode can be divided into the main release period and the residual release period. The seismic activity level during the main periods is much higher than that during the residual periods and all earthquakes with Ms ≥ 6.0 occurred in the main release periods. The earthquake occurrence shows an obvious pseudo-periodicity during the main release periods. The duration of a main period is about twice as long as that of the residual release period. (2) The criteria that indicates the transition from a main release period to a residual release period is: 1) the time interval between the last Ms ≥ 5.0 earthquake during the main release period and the first Ms ≥ 5.0 earthquake of the following residual release period is much longer than the maximum time interval of the Ms ≥ 5.0 earthquakes occurred during the main period; 2) an Ms ≥ 6.0 earthquake may occur about two years before the last Ms ≥ 5.0 earthquake of the main period. (3) The Y-Y seismic zone is divided into four areas: the sea area of northern sag to the north of 35ºN, the sea area of southern sag to the south of 34ºN and the offshore area of Yangtze estuary, lower Yangtze block to the east of Tanlu fault (PTLF), and Qinling-Dabie block. The seismic activity level in the sea areas is higher than that on the lands and the highest seismicity level is in the sea areas to the south of 34ºN. Except for the current episode, Ms ≥ 5.0 earthquakes have occurred in all four areas during previous episodes. (4) The current episode, which starts from 1974, likely entered into its residual release period in 1999. That period will end till 2012 and then enter into a seismically quiet episode. During this period, there may have two or three groups of earthquake with Ms ≥ 5.0, but the maximum magnitude will be lower than Ms6.0. According to the possibility order of the occurrence of future mid-strong earthquakes, the four areas can be arranged as: the sea area of southern sag to the south of 34ºN, the lower Yangtze block, the sea area of northern sag to the north of 35ºN, and the Qinling-Dabie block (from high to low).Finally, based on all above work, we determine three seismic risk zones where mid-strong earthquakeswhich will cause damages may occur within the next 10 years. Those risk zones are: 1) southern sags of Southern Yellow sea and coastal regions, Ms ≥ 6; 2) Yangtze estuary and sea area to the east of it, Ms ≥ 5; 3) Changshu-Taicangarea, Ms ≥ 5 (Fig. 15).
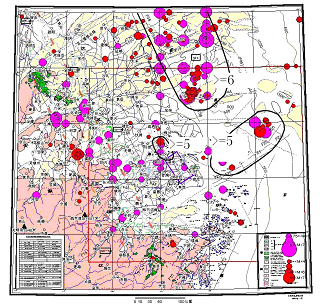 | Figure 15. Seismic risk zones |
References
| [1] | Bureau of Earthquake Damage Protection, Chinese Earthquake Administration, Catalog of Strong Earthquakes in Chinese History (23rd Century BC – 1911 AD), Earthquake Press, 1995, Beijing, China, p71 |
| [2] | R.-S. Dong, C.-H. Fu, “Textual criticism of epicenter of the October 9, 1505 63/4 earthquake”, Earthquake Research in China, 13(2), 1997, 172-178 |
| [3] | C.-S. Liu, T.-Y. Jing, Catalog of Earthquakes in Jiangsu, Zhejiang, Anhui, Shanghai (225 – 2000), Earthquake Press, 2002, Beijing, China |
| [4] | W.H.K. Lee, S.W. Stewart, Principles and Applications of Microearthquake Networks, Academic Press, 1981, New York, USA |
| [5] | B. Gutenberg, C. Ritcher, Seismicity of the Earth and Associated Phenomena, Princeton University Press, 1954, Princeton, NJ, USA |
| [6] | R.L. Burden, J.D. Faires, Numerical Analysis, Thomson Brooks/Cole, 2004, Belmont, CA, USA |
| [7] | R.A. Fisher, “On the interpretation of χ2 from contingency tables, and the calculation of P”, Journal of the Royal Statistical Society, 85(1), 1922, 87-94 |
| [8] | A.Venkataraman, “Investigating the mechanics of earthquakes using macroscopic seismic parameters”, Doctorate Thesis, California Institute of Technology, Pasadena, California, 2002 |
| [9] | T. Lidaka, A. Kato, E. Kurashimo, T. Iwasaki, N. Hirata, H. Katao, I. Hirose, H.Miyamachi, “Fine structure of P-wave velocity distribution along the Atotsugawa fault, central Japan”, Tectonophysics, 472(1-4), 2009, 95-104 |
| [10] | F.-T. Wu, A.L. Levshin, V.M. Kozhevnikov, “Rayleigh wave group velocity tomography of Siberia, China and the Vicinity”, Pure and Applied Geophysics, 149(3), 1997, 447-473 |
| [11] | Z.-K. Liu, W. Wang, R. Zhang, N.-H. Yu, J.-Y. Pan, “A seismogram digitization and database management system”, ACTA SeismologicaSinica, 23(3), 2001, 314-321 |
| [12] | W.-L. Liu, J.-Z. Wang, Y.-W. Chen, X.-S. Ling, X.-W. He, D.-W. Liu, “Analysis on errors in study on the fracture feature of moderate and small earthquakes occurred near seismic belts and gaps”, Northwestern Seismological Journal, 23(3), 2001, 224-229 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML