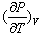Mbane Biouele César
Laboratoire de Physique de l’Atmosphère Terrestre, B.P. 812 Faculté des Sciences de l’Université de Yaoundé I-Cameroun
Correspondence to: Mbane Biouele César, Laboratoire de Physique de l’Atmosphère Terrestre, B.P. 812 Faculté des Sciences de l’Université de Yaoundé I-Cameroun.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Clausius-Clapeyrons’ formulas show precisely that, unlike dry water vapor that can be assimilated to the ideal gas at all circumstances, saturated water vapor has, in an air parcel at the same time very cold (temperatures below 0.0098℃) and rich in moisture (vapor pressure above 6.11 mb), thermoelastic properties diametrically opposed to those of ideal gas (including dry water vapor). Given the fact that saturated water vapor is known as the birthplace of meteorological events such as thunderclouds and electrical processes related, we want to make a contribution to a better understanding of lightning flashes triggered by major tropical disturbances such as cyclones or hurricanes. Taking into account the vertical profiles of temperature and water vapor in the troposphere leads to localization of the region in which the ideal gas assumption should be banned, hence the appropriate repartition of electrical charges within thunderclouds and the better understanding of related lightning flashes.
Keywords:
Vertical profiles of thunderclouds, Electrical charges, Lightning flashes
Cite this paper: Mbane Biouele César, Physics of Atmosphere Dynamic or Electric Balance Processes Such as Thunderclouds and Related Lightning Flashes, Geosciences, Vol. 2 No. 1, 2012, pp. 6-10. doi: 10.5923/j.geo.20120201.02.
1. Introduction
In this work, regardless of the manner in which the tropical depressions are consider[1-14], we want to make a contribution to a better understanding of physics behind these atmospheric events with high destructive power and their related clouds that trigger electrical processes. Our results are obtained from effectiveness of fluid dynamic balance (i.e.: at any moment, the particle of fluid has the same pressure as its environment) that leads to Clausius-Clapeyrons’ diagram which shows precisely that, unlike the dry water vapor that can be assimilated to the ideal gas at all times, saturated water vapor at low temperatures (temperatures below 0.0098℃) in the presence of high humidity (vapor pressure above 6.11 mb) of air, has thermoelastic properties diametrically opposed to those of ideal gases (including dry water vapor). In tropical regions, saturated water vapor occupies the middle and top of the troposphere to more than 90% (remember here that saturated water vapor is known as the birthplace, home or bed of weather events such as clouds and (electrical or thermodynamic) processes related. From that moment, it was necessary to resort the thermodynamic properties of saturated water vapor to understand of physics behind tropical depressions and related clouds that trigger electrical processes.
2. Mbanes’ Equation of Fluid Dynamic Balance
Atmospheric dynamics uses a very precise concept of particle of air[15-18]. Namely:(a) Few exchanges on molecular scale: one can follow a quantity of air which preserves certain properties.(b) Quasi-static equilibrium: there is at any moment dynamic balance, the particle has the same pressure as its environment (P=Pext).(c) No thermal balance: the heat transfers by conduction are very slow and are neglected. One can have T≠ Text.(d) The size of the particle can go from a few cm to 100 km according to the applications.Taking into account the fact that the atmosphere is mainly composed of dry air and water vapor, the Dalton’s law connects the pressure (P) with the partial pressure of dry air (Pa) and water vapor (ew) 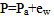 | (1) |
In deriving (P) with respect to the temperature, one has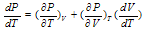 | (2) |
According to the Quasi-static equilibrium (or dynamic balance) the pressure of the parcel of air must be the same as that of the ambient air, including during sudden changes in phases by water it contains. In other words, the pressure (P) of the parcel of air remains constant during changes in phases. Hence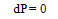 | (3) |
Equations (2) and (3) lead to the derivative of V compared to T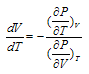 | (4) |
Introducing the coefficient of thermal expansion of moist air at constant temperature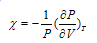 | (5) |
Then the Mbanes’ equation of fluid dynamic balance: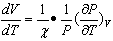 | (6) |
One can also write equation of fluid dynamic balance in terms of (7)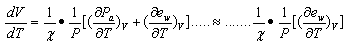 | (7) |
The Clausius-Clapeyron relations (illustrated by saturation vapor pressure line of Fig.1a) show that the derivative of the pressure (P) compared to T and the derivative of water vapor (ew) compared to T have the same sign, given their current values in the troposphere.Mbanes’ equations (6-7) are fundamental to the dynamics of atmosphere because they help to know the sign of 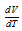 (the derivative of the volume (V) of a parcel of moist air, compared to T) under all conditions of temperature and vapor pressure possible in the atmosphere. Equations (6 and 7) are also prognostic because they predict in which direction the air parcel will move (up or down) if temperature increases or decreases. Table 1 provides an overview of possible situations in the atmosphere.
(the derivative of the volume (V) of a parcel of moist air, compared to T) under all conditions of temperature and vapor pressure possible in the atmosphere. Equations (6 and 7) are also prognostic because they predict in which direction the air parcel will move (up or down) if temperature increases or decreases. Table 1 provides an overview of possible situations in the atmosphere.| Table 1. Pressure variation of a constant volume of moist air, depending on the temperature T: in specific regions of the Troposphere, delimited by 0.0098°C and 6.11 mb characteristic surfaces |
| | Range of Temperature (℃) | T < 0.0098 | T < 0.0098 | T > 0.0098 | | Range of Vapor pressure (mb) | ew < 6.11 | ew > 6.11 | ew > 6.11 |
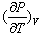
| ﹢ | - | ﹢ |
|
|
Table 1 can be reproduced an infinite number of times from an original simple experiment[14] during which the students realize the pressure variations of a constant volume of moist air locked in a half bottle of mineral water. The device that they used for this experiment is exposed as a first step to solar radiation, and then placed in a refrigerator. The ranges of temperature and humidity are those used by Clapeyron on Fig.1a.The results of our experiment are always in good agreement with the slopes of the various saturation curves obtained in the case of water substance thermodynamics (Fig.1a). These slopes confirm the existence of cold advection and hot subsidence, in regions where temperatures are less than 0.0098℃ and at the same time, vapor pressures greater than 6.11 mb. The presence in the troposphere of 0.0098℃ isotherm and 6.11 mb pseudo-isobar is necessary for the formation of Cyclones or hurricane.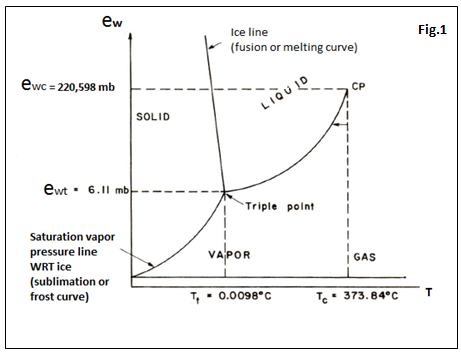 | Figure 1a. the projection of the ewαT-surface for water substance onto the ew T-plane |
3. Hydrodynamic Profile of Troposphere
Table 1 leads to a very new partition of the troposphere (Fig.1b): In regions (I) and (III) one can observe hot advection and cooler subsidence (that looks evident). Now, things have to change: In region (II), hot subsidence and cooler advection are predicted.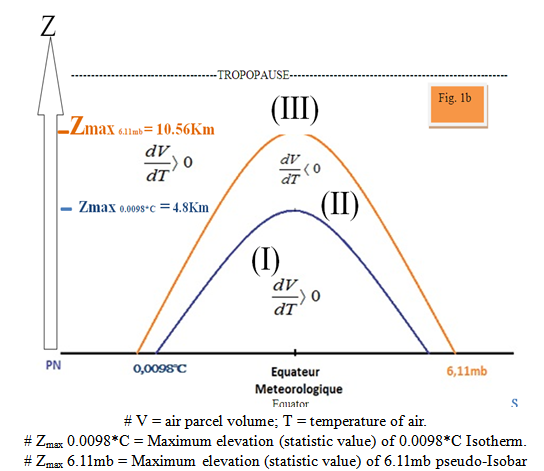 | Figure 1b. Specific regions of the troposphere limited by water vapor critical surfaces |
4. Kinematics of Cyclones, Hurricanes, Related Clouds and Polarities
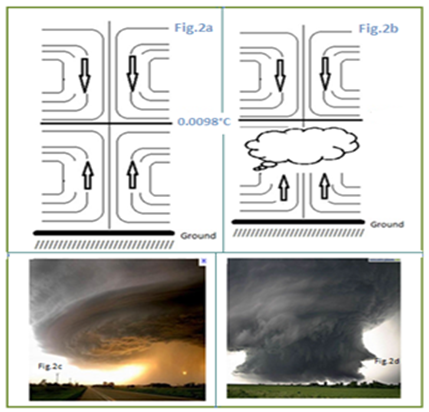 | Figure 2. Vertical profiles of hurricanes and clouds related. Proofed illustrations |
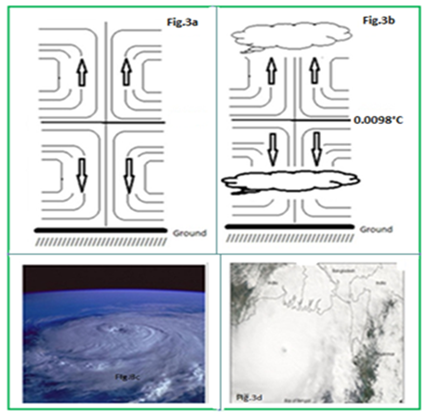 | Figure 3. Vertical profiles of cyclones and clouds related - proofed illustrations |
Base on the results of Table 1 and under the relation (6) linking 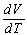 with
with 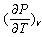 , it is now possible to divide the Atmosphere into three regions: two regions where the volume (V) and temperature (T) of particles of air vary in the same direction (i.e.:
, it is now possible to divide the Atmosphere into three regions: two regions where the volume (V) and temperature (T) of particles of air vary in the same direction (i.e.: 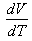 > 0) and one region where the volume (V) and temperature (T) of particles of air vary in the opposite direction (i.e.:
> 0) and one region where the volume (V) and temperature (T) of particles of air vary in the opposite direction (i.e.: 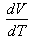 < 0). Taking into account the fact that the exchange of matter between the particles of air and the surroundings environment is very slow (according to part (a) of Atmospheric dynamics concept of particle of air), any increase in volume (V) leads to a depletion in density () which triggers the movement of the parcel of air to higher altitudes. On the other hand, any decrease in volume (V) leads to an increase in density which triggers the movement of the parcel to lower altitudes.Essentially the tropical depressions are heat engines, which imply the existence of a heat source or a cold source. Knowing how (V) depends on (T) across the troposphere, helps to built the vertical profile of the winds observed in Hurricanes (Figs.2(a-d)) which interior is warmer than its environment; or vertical profile of the winds observed in Cyclones (Fig.3(a-d)) which interior is cooler than its environment.Thunderclouds, electric fields and charges, lightning are related phenomena triggered by tropical depressions with respect to water substance thermodynamics (Figures 4).
< 0). Taking into account the fact that the exchange of matter between the particles of air and the surroundings environment is very slow (according to part (a) of Atmospheric dynamics concept of particle of air), any increase in volume (V) leads to a depletion in density () which triggers the movement of the parcel of air to higher altitudes. On the other hand, any decrease in volume (V) leads to an increase in density which triggers the movement of the parcel to lower altitudes.Essentially the tropical depressions are heat engines, which imply the existence of a heat source or a cold source. Knowing how (V) depends on (T) across the troposphere, helps to built the vertical profile of the winds observed in Hurricanes (Figs.2(a-d)) which interior is warmer than its environment; or vertical profile of the winds observed in Cyclones (Fig.3(a-d)) which interior is cooler than its environment.Thunderclouds, electric fields and charges, lightning are related phenomena triggered by tropical depressions with respect to water substance thermodynamics (Figures 4).
5. Conclusions and Perspectives
The thermodynamics of saturated water vapor is ignored by meteorologists and rarely used in climate models. However, the results presented in this work, demonstrate its effectiveness. To attract the attention of each other on the importance of temperature and winds profiles attributed by us to cyclones and hurricanes, we offer the following views:(i) Speculation on the origin of electric charges and the events that result must stop and allow each of us to seek ways of preventing the propagation of cyclones or hurricanes: as is done already to contain forest fires. A reflection on the subject is engaged in our research team.(ii) Now we know how the volume of the particle of air varies when its temperature increases or decreases, in any part of the atmosphere. Vertical movement that results can be predicted.(iii) Now we distinguish perfectly warm depression (Hurricanes) compared to cold depression (Cyclones). (iv) It is now possible for all of us to use our common sense, to seek ways of preventing the extent of damage caused by the tropical depression. (v) We can predict obvious consequence of global warming: the frequency of occurrence of tropical depression will be higher and many more areas affected, including those that are spared at this time.(vi) Airline pilots will be better informed when approaching the turbulence generated by the warm or cold depression.(vii) According to Mbane [14]: the updrafts are the drivers of tropical depressions. Their fuel is water vapor and they are subject to the Coriolis force (F=-2Ω×Vupdrafts) that deviates systematically these disturbances to the west, both in the northern than in the southern hemisphere. The base currents of the atmospheric general circulation inhibit or promote this movement.To summarize, these results can be placed side by side with ground-or space- based observations, to develop a solid theory on physical mechanism pertaining to the lifecycle of cyclones, hurricanes or related atmosphere electric balance processes such as thunderstorms’ lightning flashes.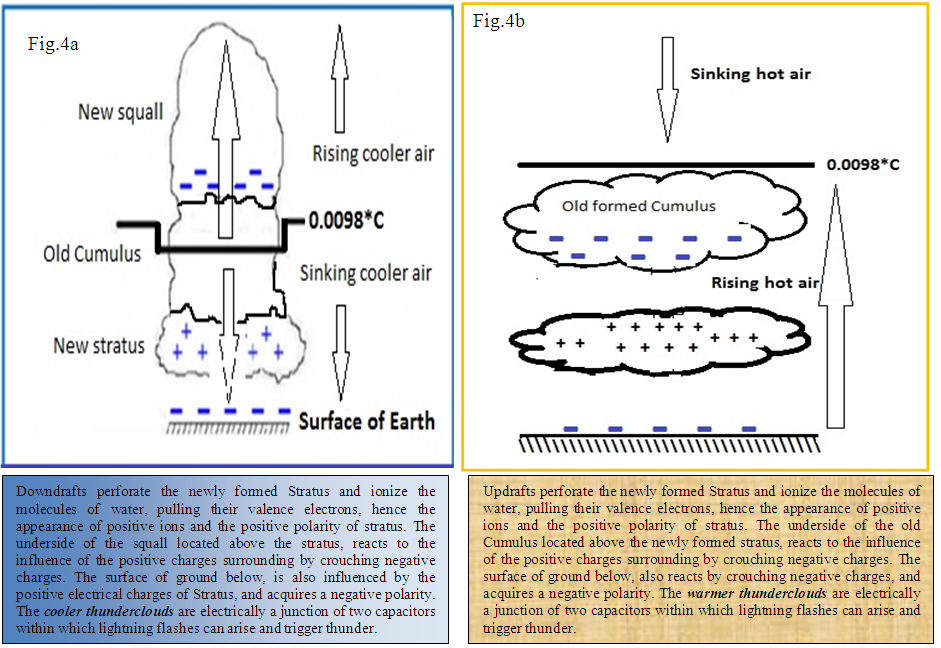 | Figure 4. a. Downdrafts perforate the newly formed Stratus and ionize the molecules of water, pulling their valence electrons, hence the appearance of positive ions and the positive polarity of stratus. The underside of the squall located above the stratus, reacts to the influence of the positive charges surrounding by crouching negative charges. The surface of ground below, is also influenced by the positive electrical charges of Stratus, and acquires a negative polarity. The cooler thunderclouds are electrically a junction of two capacitors within which lightning flashes can arise and trigger thunder. b. Updrafts perforate the newly formed Stratus and ionize the molecules of water, pulling their valence electrons, hence the appearance of positive ions and the positive polarity of stratus. The underside of the old Cumulus located above the newly formed stratus, reacts to the influence of the positive charges surrounding by crouching negative charges. The surface of ground below, also reacts by crouching negative charges, and acquires a negative polarity. The warmer thunderclouds are electrically a junction of two capacitors within which lightning flashes can arise and trigger thunder. |
ACKNOWLEDGEMENTS
Author of this paper gratefully acknowledge the following University Institutions and Professors: (1) The University of California in Los Angeles (USA) who kindly provided a geospatial measurement station called “AMBER MAGNETOMETER” to the University of Yaoundé I (Cameroon). (2) The Air Force Research Laboratory (Boston University), which has equipped the University of Yaoundé I, with a geospatial measuring station called “SCINDA SENSOR” and the University of Yaoundé I (Cameroon), which offered modern facilities with Internet connection, to accommodate both stations. (3) Professors : Mark B. Moldwin (Atmospheric-Oceanic and Space Sciences Research Laboratory, University of Michigan (USA)); Christine Mazaudier ( Laboratoire de Physique des Plasmas-Ecole Polytechnique (France)); Frederic Ouattara (Burkina Faso); Endawoke Gizangaw ( Institute for Scientific Research, USA) ; Doumbia Vafi (Ivory Coast); Houngninou Etienne (Benin), for their kind collaboration.
References
| [1] | G. O. P. Obasi, Intertropical meteorology meeting, Nairoby, Kenya (1974). |
| [2] | Norquist et al, MWR, 1977,105, pp. 334-342. |
| [3] | T.D. Keenan, Quart. J. Roy. Met. Soc., 1992, 118, pp. 283-326. |
| [4] | P. de Felice, CEPADUES, 1992, pp. 59-68. |
| [5] | H. Riehl, Tropical meteorology, Mc Graw-Hill, New York, 1954, 392. |
| [6] | C. G. Rossby, Yearbook of Agriculture, U.S. Department of Agriculture, 1941, pp. 599-655. |
| [7] | P. Bradshaw, Introduction to turbulence and its measurement, Pergamon Press, 1971. |
| [8] | L. Rosenhead, Laminar boundary layers, Oxford University Press , 1963, 242. |
| [9] | H. R. Byers, General Meteorology, McGraw-Hill Book Company Inc, 1959, 540. |
| [10] | A. Arakawa, Journal of Computations Physics, 1966, 1, pp. 119-143. |
| [11] | G. K. Batchelor, An Introduction to Fluids Dynamics, Cambridge University Press, 1967, 468. |
| [12] | C. A. Riegel, Fundamentals of Atmospheric Dynamics and Thermodynamics, World Scientific Publishing Co. Pte. Ltd, 1992, 496. |
| [13] | C. B. Mbane, International Journal of Physical Sciences (IJPS), 2009, 4, pp. 242-246. |
| [14] | C. B. Mbane, Doctoral thesis (thèse d’Etat), Univ. of Yaounde I, Yaounde, Cameroun, 2005. |
| [15] | H. Lumbroso, Thermodynamique-100 exercices et Problèmes résolues, Math Sup. Ediscience/McGraw-Hill, 1973, 360. |
| [16] | R. Comolet and J. Bonnin, Mécanique Expérimentale des Fluides (Tome III-Recueil d’Exercices), Masson 5e ed., 1992, 264. |
| [17] | G. T. Csanady, Theory of Turbomachines, McGraw-Hill, 1964. |
| [18] | C. B. Mbane et al., Scholar Research Library, coming issue of Archive of Physics Research, Vol 2, Issue 4, release in December 2011. |

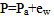
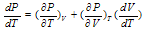
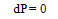
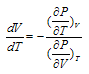
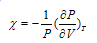
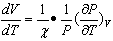
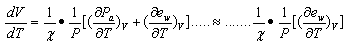
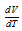 (the derivative of the volume (V) of a parcel of moist air, compared to T) under all conditions of temperature and vapor pressure possible in the atmosphere. Equations (6 and 7) are also prognostic because they predict in which direction the air parcel will move (up or down) if temperature increases or decreases. Table 1 provides an overview of possible situations in the atmosphere.
(the derivative of the volume (V) of a parcel of moist air, compared to T) under all conditions of temperature and vapor pressure possible in the atmosphere. Equations (6 and 7) are also prognostic because they predict in which direction the air parcel will move (up or down) if temperature increases or decreases. Table 1 provides an overview of possible situations in the atmosphere.



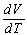 with
with 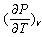 , it is now possible to divide the Atmosphere into three regions: two regions where the volume (V) and temperature (T) of particles of air vary in the same direction (i.e.:
, it is now possible to divide the Atmosphere into three regions: two regions where the volume (V) and temperature (T) of particles of air vary in the same direction (i.e.: 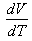 > 0) and one region where the volume (V) and temperature (T) of particles of air vary in the opposite direction (i.e.:
> 0) and one region where the volume (V) and temperature (T) of particles of air vary in the opposite direction (i.e.: 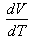 < 0). Taking into account the fact that the exchange of matter between the particles of air and the surroundings environment is very slow (according to part (a) of Atmospheric dynamics concept of particle of air), any increase in volume (V) leads to a depletion in density () which triggers the movement of the parcel of air to higher altitudes. On the other hand, any decrease in volume (V) leads to an increase in density which triggers the movement of the parcel to lower altitudes.Essentially the tropical depressions are heat engines, which imply the existence of a heat source or a cold source. Knowing how (V) depends on (T) across the troposphere, helps to built the vertical profile of the winds observed in Hurricanes (Figs.2(a-d)) which interior is warmer than its environment; or vertical profile of the winds observed in Cyclones (Fig.3(a-d)) which interior is cooler than its environment.Thunderclouds, electric fields and charges, lightning are related phenomena triggered by tropical depressions with respect to water substance thermodynamics (Figures 4).
< 0). Taking into account the fact that the exchange of matter between the particles of air and the surroundings environment is very slow (according to part (a) of Atmospheric dynamics concept of particle of air), any increase in volume (V) leads to a depletion in density () which triggers the movement of the parcel of air to higher altitudes. On the other hand, any decrease in volume (V) leads to an increase in density which triggers the movement of the parcel to lower altitudes.Essentially the tropical depressions are heat engines, which imply the existence of a heat source or a cold source. Knowing how (V) depends on (T) across the troposphere, helps to built the vertical profile of the winds observed in Hurricanes (Figs.2(a-d)) which interior is warmer than its environment; or vertical profile of the winds observed in Cyclones (Fig.3(a-d)) which interior is cooler than its environment.Thunderclouds, electric fields and charges, lightning are related phenomena triggered by tropical depressions with respect to water substance thermodynamics (Figures 4).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML