-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2019; 9(1): 1-4
doi:10.5923/j.fs.20190901.01

The Charged Higgs-like Bosons Have Already Been Observed by the ATLAS and CMS Collaborations
Mario Everaldo de Souza
Departamento de Fisica, Universidade Federal de Sergipe, São Cristovão, Sergipe, Brazil
Correspondence to: Mario Everaldo de Souza, Departamento de Fisica, Universidade Federal de Sergipe, São Cristovão, Sergipe, Brazil.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Taking into account a very solid quark compositeness model, based on the electrical charge densities of the nucleons found by R. Hofstadter, R. Herman, L. Durand and R. R. Wilson in the early 1960s, from which a new quantum number is deduced, and the experimental data on the Higgs boson obtained by the ATLAS and CMS Collaborations, this article shows that these collaborations have already seen the charged Higgs-like bosons by means of the WW channel. The data also imply that the charged and neutral Higgs-like bosons have similar masses, and that the Higgs-like bosons have odd parity like the other fundamental bosons of Nature. The ratio between the productions of charged to neutral Higgs-like bosons is calculated.
Keywords: Charged Higgs-like Bosons, Higgs-like Boson, Higgs Boson
Cite this paper: Mario Everaldo de Souza, The Charged Higgs-like Bosons Have Already Been Observed by the ATLAS and CMS Collaborations, Frontiers in Science, Vol. 9 No. 1, 2019, pp. 1-4. doi: 10.5923/j.fs.20190901.01.
Article Outline
1. Introduction
- In 2012 the ATLAS and CMS collaborations announced the remarkable discovery of a boson resembling the long sought Higgs boson of the Standard Model of Particle Physics [1, 2, 3] with a mass of about 125 GeV. That is why it has been called a Higgs-like boson.Since then the Higgs-like boson has been observed in the channels
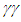 , ZZ, WW,
, ZZ, WW, 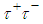 and b+b- [4].It is important to have in mind that the Standard Model does not provide any Higgs boson quantum number, so that the above Higgs decay modes are not explained in terms of selection rules dictated by Higgs quantum numbers.On the other hand, taking into account the distributions of electrical charges inside the nucleons, as found by R. Hofstadter, R. Herman, L. Durand and R. R. Wilson [5, 6, 7, 8], which are shown below in Figure 1, de Souza proposed in 2005 [9] that each quark is composed of two prequarks (called primons). Since then the compositeness model has been improved and proven to be more consistent with the experimental results.According to the model there is a new quantum number
and b+b- [4].It is important to have in mind that the Standard Model does not provide any Higgs boson quantum number, so that the above Higgs decay modes are not explained in terms of selection rules dictated by Higgs quantum numbers.On the other hand, taking into account the distributions of electrical charges inside the nucleons, as found by R. Hofstadter, R. Herman, L. Durand and R. R. Wilson [5, 6, 7, 8], which are shown below in Figure 1, de Souza proposed in 2005 [9] that each quark is composed of two prequarks (called primons). Since then the compositeness model has been improved and proven to be more consistent with the experimental results.According to the model there is a new quantum number 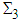 directly related to quark compositeness, and because of its existence, the Higgs-like boson is, actually, a multiplet. The model shows that this new quantum number is the reason behind the weak decays of hadrons [10] as shown below in Table 1. Please, see more details and other tables in reference [10].As argued in the paper presented at Moriond 2014 [11], it is important to emphasize that the model agrees very well with Miller analysis [12] of the charge density in the center of the neutron, as he found a total charge of –(1/3)e inside its central positive core. The central hard core with a radius of about 0.2 fm has also been observed by many experiments at CERN and Fermilab along the years. In 2011 and 2013 it was observed by the TOTEM collaboration at 7 TeV [13, 14] and 8 TeV [15].
directly related to quark compositeness, and because of its existence, the Higgs-like boson is, actually, a multiplet. The model shows that this new quantum number is the reason behind the weak decays of hadrons [10] as shown below in Table 1. Please, see more details and other tables in reference [10].As argued in the paper presented at Moriond 2014 [11], it is important to emphasize that the model agrees very well with Miller analysis [12] of the charge density in the center of the neutron, as he found a total charge of –(1/3)e inside its central positive core. The central hard core with a radius of about 0.2 fm has also been observed by many experiments at CERN and Fermilab along the years. In 2011 and 2013 it was observed by the TOTEM collaboration at 7 TeV [13, 14] and 8 TeV [15].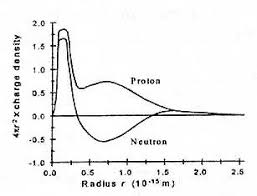 | Figure 1. Electrical charge distributions in the nucleons |
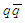 pairs are incompatible with Figure 1 above because according to R. Hofstadter, R. Herman, L. Durand and R. R. Wilson findings the hard core has a total charge of +(1/2)e and not +1e.It is also worth recalling that charges do not appear in Bjorken scaling structure functions. Thus, at high q2 the de Broglie wavelength h/q is very small and, then, when the 3 inner prequarks are probed they are identified as being 3 valence quarks due to the lack of identification of their charges. Therefore, there is a complete entanglement between prequarks and valence quarks. And true quarks should be the so-called constituent quarks. Therefore, the quark compositeness scale is just 1-10 GeV and not the extremely high scales that have been considered in the searches for quark compositeness. The null results of such searches mean, actually, that primons are elementary.As shown in reference [16] the quark compositeness model above presented solves a quite large number of problems in Particle Physics, such as the proton spin puzzle, the number of quarks, the origin of the Cabibbo factors, the EMC effect, and the Krisch effect.
pairs are incompatible with Figure 1 above because according to R. Hofstadter, R. Herman, L. Durand and R. R. Wilson findings the hard core has a total charge of +(1/2)e and not +1e.It is also worth recalling that charges do not appear in Bjorken scaling structure functions. Thus, at high q2 the de Broglie wavelength h/q is very small and, then, when the 3 inner prequarks are probed they are identified as being 3 valence quarks due to the lack of identification of their charges. Therefore, there is a complete entanglement between prequarks and valence quarks. And true quarks should be the so-called constituent quarks. Therefore, the quark compositeness scale is just 1-10 GeV and not the extremely high scales that have been considered in the searches for quark compositeness. The null results of such searches mean, actually, that primons are elementary.As shown in reference [16] the quark compositeness model above presented solves a quite large number of problems in Particle Physics, such as the proton spin puzzle, the number of quarks, the origin of the Cabibbo factors, the EMC effect, and the Krisch effect.
|
2. A New Quantum Number
- The main results for the quantum numbers of quarks and for the Higgs-like bosons are presented below in some tables and in a diagram. For details, please take a look at the corresponding references and at the web page www.primons.com.
2.1. The 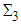 Quantum Numbers for Quarks
Quantum Numbers for Quarks
- The
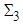 quantum numbers for quarks (Table 2) were calculated in references [9, 10, 11, 16].
quantum numbers for quarks (Table 2) were calculated in references [9, 10, 11, 16]. 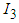 is the well known isospin.
is the well known isospin.
|
2.2. The Higgs-like Boson Multiplet with its Quantum Numbers, Spins and Electrical Charges
- The
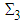 quantum numbers for the Higgs-like bosons and their spins (Table 3) were calculated in references [11, 16].
quantum numbers for the Higgs-like bosons and their spins (Table 3) were calculated in references [11, 16].
|
2.3. The Generators of Quark Masses
- Table 4 below was taken from reference [16].
|
2.4. The Quark Transitions by Means of Virtual Higgs-like Bosons
- With the
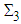 assignments for quarks and for Higgs-like bosons we can construct the diagram below shown in Figure 2 for the virtual transitions between quarks mediated by Higgs-like bosons (to lowest order). The diagram was published in reference [11].With respect to the diagram below, the BaBar Collaboration [17] has found an excess in the decay
assignments for quarks and for Higgs-like bosons we can construct the diagram below shown in Figure 2 for the virtual transitions between quarks mediated by Higgs-like bosons (to lowest order). The diagram was published in reference [11].With respect to the diagram below, the BaBar Collaboration [17] has found an excess in the decay 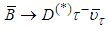 that points in the direction of the charged Higgs-like boson
that points in the direction of the charged Higgs-like boson 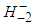 . In terms of quarks and primons this decay means
. In terms of quarks and primons this decay means 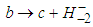 and
and 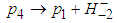 where
where 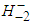 is a virtual particle. In terms of
is a virtual particle. In terms of 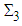 this decay means −1 = +1 + (−2). Therefore, in this decay due to a
this decay means −1 = +1 + (−2). Therefore, in this decay due to a 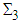 current, there is the mediation of the Higgs-like boson
current, there is the mediation of the Higgs-like boson 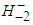 . Taking into account the results of this paper and the above argumentation, BaBar can claim that it was the first to discover the charged Higgs-like bosons
. Taking into account the results of this paper and the above argumentation, BaBar can claim that it was the first to discover the charged Higgs-like bosons 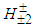 .
.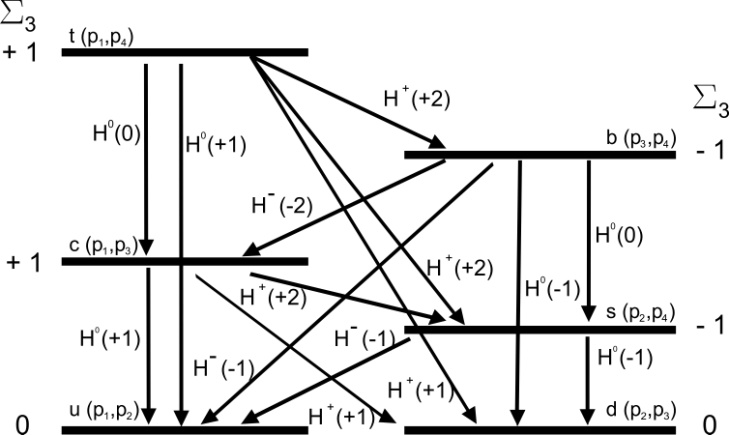 | Figure 2. The quark transitions via virtual Higgs-like bosons |
3. Identification of the Neutral and Charged Higgs-like Bosons
- It is important to have in mind that according to the quark compositeness model strong interactions conserve
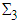 while weak interactions do not. Taking into account Figure 1 above and the quark electrical charges de Souza proposed the structure for the proton shown in Figure 3 below which first appeared in reference [10] and later on in reference [16]. Let us, hence, now understand how the charged and neutral Higgs-like bosons are produced. Below only lowest order processes are considered. Of course, during the extremely short collision time the proton structure shown in Figure 3 below is completely disturbed and disrupted.
while weak interactions do not. Taking into account Figure 1 above and the quark electrical charges de Souza proposed the structure for the proton shown in Figure 3 below which first appeared in reference [10] and later on in reference [16]. Let us, hence, now understand how the charged and neutral Higgs-like bosons are produced. Below only lowest order processes are considered. Of course, during the extremely short collision time the proton structure shown in Figure 3 below is completely disturbed and disrupted. | Figure 3. The structure of the proton in terms of quarks and primons (prequarks). Of course, this is just a pictorial representaion in two dimensions of the two 3-dimensional layers of primons |
 :Taking into account Table 4 above,
:Taking into account Table 4 above,  is formed by means of the interaction between p2 and p3 either from the same proton or from different protons in proton-proton collisions. We may symbolize this interaction by
is formed by means of the interaction between p2 and p3 either from the same proton or from different protons in proton-proton collisions. We may symbolize this interaction by 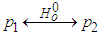 Hence, the
Hence, the  boson can be more identified with the Standard Model Higgs boson. After its formation it decays in
boson can be more identified with the Standard Model Higgs boson. After its formation it decays in  , in Z0 or in b+b-. Therefore, to lowest order the process is not
, in Z0 or in b+b-. Therefore, to lowest order the process is not 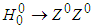 and thus, the intermediate state
and thus, the intermediate state 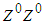 comes about from 2 different
comes about from 2 different 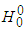 decays.2) The charged bosons
decays.2) The charged bosons 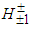 and
and 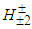 :Similarly to the formation of
:Similarly to the formation of 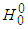 above, considering Table 4, the bosons
above, considering Table 4, the bosons 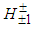 are formed by means of the interaction between p1 and p3 either from the same proton or from different protons. We may symbolize the interaction by
are formed by means of the interaction between p1 and p3 either from the same proton or from different protons. We may symbolize the interaction by 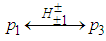 The same holds for
The same holds for 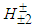 which is formed via the interaction between p1 and p2 either from the same proton or from different protons. The bosons
which is formed via the interaction between p1 and p2 either from the same proton or from different protons. The bosons 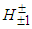 and
and 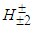 may decay to
may decay to 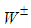 through the interactions
through the interactions 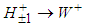 and
and 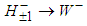 with
with 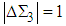 , and
, and 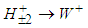 and
and 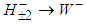 with
with 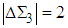 . Each pair of
. Each pair of 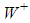 and
and 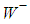 generated may look like as having been originated from the off-shell decay
generated may look like as having been originated from the off-shell decay 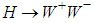 . That is the source of the confusion for the experimentalists. Maybe a more precise analysis of the jet angles of W bosons may clear up this imbroglio.Let us now estimate the relative productions of all these bosons. Each proton has two p1p2 pairs, so that in each proton there is the production of 4
. That is the source of the confusion for the experimentalists. Maybe a more precise analysis of the jet angles of W bosons may clear up this imbroglio.Let us now estimate the relative productions of all these bosons. Each proton has two p1p2 pairs, so that in each proton there is the production of 4 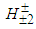 , and between the different protons there are 12 p1p2 pairs. Therefore, we have the total production of 16
, and between the different protons there are 12 p1p2 pairs. Therefore, we have the total production of 16 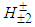 . As to p1p3 there are only 4 possible pairs (formed due to the proton structure disruption during the collision), and thus there is the total production of only 4
. As to p1p3 there are only 4 possible pairs (formed due to the proton structure disruption during the collision), and thus there is the total production of only 4 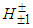 bosons. By the same token, in the case of p2p3 there are 14 possible pairs, so that there is the total production of 14
bosons. By the same token, in the case of p2p3 there are 14 possible pairs, so that there is the total production of 14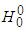 . Therefore, the relative production of WW pairs to ZZ pairs is about 1.43 which is a number that is within the experimental results up to now. And in the WW signal we have ¼ of
. Therefore, the relative production of WW pairs to ZZ pairs is about 1.43 which is a number that is within the experimental results up to now. And in the WW signal we have ¼ of 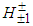 and ¾ of
and ¾ of 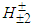 .Therefore, when only the
.Therefore, when only the 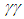 and ZZ channels are considered we measure only the
and ZZ channels are considered we measure only the 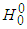 boson and when the WW channel is considered we measure the charged Higgs-like bosons in the proportions shown above.Although CMS claimed to have found in 2013 an excess of events WW [18], it was the ATLAS detector that performed a more precise observation of the Higgs boson decay to WW in 2015 [19]. Therefore, ATLAS actually observed the charged Higgs-like bosons
boson and when the WW channel is considered we measure the charged Higgs-like bosons in the proportions shown above.Although CMS claimed to have found in 2013 an excess of events WW [18], it was the ATLAS detector that performed a more precise observation of the Higgs boson decay to WW in 2015 [19]. Therefore, ATLAS actually observed the charged Higgs-like bosons 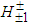 and
and 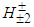 . The reported mass of 125.36 GeV by ATLAS means that the masses of the charged bosons are similar to that of the neutral boson
. The reported mass of 125.36 GeV by ATLAS means that the masses of the charged bosons are similar to that of the neutral boson 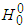 .In the light of what was shown above we can also say that the
.In the light of what was shown above we can also say that the 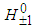 bosons have not yet been observed.
bosons have not yet been observed.4. Consequences for Parity
- It is well known that all fundamental bosons have negative parity, actually, almost all mesons. The only identified scalar meson is the resonance K0*(1430) and all the other possible candidates are all resonances: K0*(800), f0(500), f0(980) etc. Therefore, we should ask the very important question: why a fundamental boson such as the Higgs boson would be the only exception? As seen above it is not an exception: the Higgs-like bosons have odd parity. We see this easily if we admit that CP is a good symmetry in the Higgs-like decays above shown.
5. Conclusions
- Considering the whole consistency of the quark compositeness model proposed by de Souza, we can say that the ATLAS and CMS collaborations have already observed the charged Higgs-like bosons
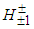 and
and 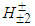 . The data also allow us to say that the neutral and charged Higgs-like bosons have similar masses. The relative production of WW pairs to ZZ pairs is about 1.43 which is a number that is within the experimental results up to now. It is also concluded that the Higgs-like bosons are pseudo-scalar bosons.
. The data also allow us to say that the neutral and charged Higgs-like bosons have similar masses. The relative production of WW pairs to ZZ pairs is about 1.43 which is a number that is within the experimental results up to now. It is also concluded that the Higgs-like bosons are pseudo-scalar bosons. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
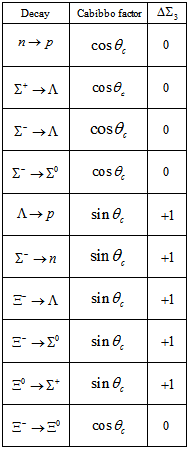
 for quarks
for quarks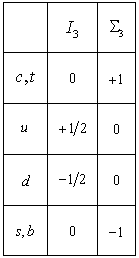

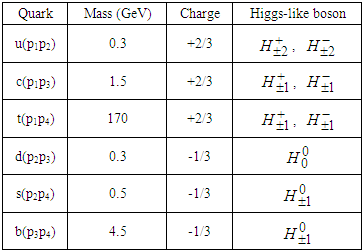
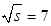 TeV with the ATLAS detector, Phys. Rev. D, 86, 032003.
TeV with the ATLAS detector, Phys. Rev. D, 86, 032003.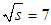 TeV, Eur. Phys. Lett., 95, 41001.
TeV, Eur. Phys. Lett., 95, 41001.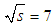 TeV, Eur. Phys. Lett., 96, 21002.
TeV, Eur. Phys. Lett., 96, 21002.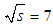 TeV, Phys. Rev. Lett., 111, 0120001.
TeV, Phys. Rev. Lett., 111, 0120001.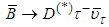 Decays, Phys. Rev. Lett., 109, 101802.
Decays, Phys. Rev. Lett., 109, 101802.