-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2017; 7(2): 27-30
doi:10.5923/j.fs.20170702.01

Coil Spring Attachement on Lathe: Evaluation of the Spring-back Effect
Olunlade B. A., Joseph S. A., Fatinikun D. E., Fadipe S. K., Bishi M. A., Aliu T. O., Odiba O.
Prototype Engineering Development Institute, National Agency for Science and Engineering Infrastructure, Ilesa, Nigeria
Correspondence to: Odiba O., Prototype Engineering Development Institute, National Agency for Science and Engineering Infrastructure, Ilesa, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A coil is created by undergoing a series of transformations from a primary to secondary structure. The primary structure is the “stock” wire, which is fabricated in linear form with a diameter (DW) of any range. The stock wire diameter, DW, is the central factor in determining coil “stiffness”. The stock wire is wound around a mandrel of varying diameter to produce the secondary structure of the coil. The stiffness of a spring is directly proportional to its spring constant (k). When a spring is coiled, its internal diameter does not assume the external diameter of the mandrel; the spring will naturally open to create a diameter larger than the form. This is probably due to the properties of the material and this effect is known as “spring-back effect’’. This paper, therefore, evaluates how varying mandrel sizes affect the air-gap created due to spring-back effect and the possibility of determining the correct mandrel size to be used in obtaining a desired spring size considering tungsten wire.
Keywords: Stock wire, Mandrel, Coil stiffness, Spring-back effect, Spring constant, Secondary structure
Cite this paper: Olunlade B. A., Joseph S. A., Fatinikun D. E., Fadipe S. K., Bishi M. A., Aliu T. O., Odiba O., Coil Spring Attachement on Lathe: Evaluation of the Spring-back Effect, Frontiers in Science, Vol. 7 No. 2, 2017, pp. 27-30. doi: 10.5923/j.fs.20170702.01.
Article Outline
1. Introduction
- Coil technology has grown substantially with manufacturers releasing different products to the market from time to time. The choice of coil depends on factors such as size, composition, stiffness, and detachment mechanism. The framework of fundamentals of coil designs helps to comprehend the practical nuances of coil development [1, 2].Metal alloys, such as nitinol, platinum, nickel, iridium, and tungsten are the primary metals used in construction of coils and are developed as alloys for optimal strength [1]. The strength of the wire used in the development of coil depends on its modulus of rigidity or shear modulus (G) which can be experimentally determined from the slope of a stress-strain curve created during torsion tests conducted on a metal sample [3]. Metal strength is determined experimentally and is referred to as the modulus of rigidity or shear modulus (G). The modulus of rigidity is the coefficient of elasticity for a shearing force, defined as the ratio of the shear stress to the shear strain [4]. A coil is created by undergoing a series of transformations from a primary (1°) to secondary (2°). The primary structure is the “stock” wire, which is fabricated in linear form with a diameter (DW) of any range. The stockwire diameter, DW, is the central factor in determining coil “stiffness” [5]. The stock wire is wound around a mandrel of varying diameter to produce the secondary structure of the coil. To understand coil stiffness, one needs to reference the physical properties of springs. The stiffness of a spring is directly proportional to its spring constant (k) [5, 6].When a spring is coiled, its internal diameter does not assume the external diameter of the mandrel; the spring will naturally open to create a diameter larger than the form. This is probably due to the properties of the material and this is known as ‘’ spring-back effect’’ [7]. Hence, the objective of this paper is to evaluate the significance of the spring-back effect on varying sizes of mandrel for spring coiling.
2. Methodology
- The methodology adopted in this paper includes:
2.1. Definition of Variables
- The factors considered in spring making are; the type of wire to use, the size of the wire, number of coils, length of spring and size of mandrel. Since the work is about spring-back effect on transformation from primary to secondary structure, the number of coils and length of spring are not necessary factors to be considered.The internal diameter of the coiled spring is the sum of the desired diameter of the spring and the air-gap created as a result of the spring-back effect [8], that is;
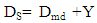 | (1) |
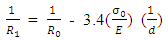 | (2) |
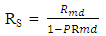 | (3) |
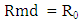 is the radius of the mandrel used in making the spring,In this paper, C is given as the spring constant, as obtained from equation 4;
is the radius of the mandrel used in making the spring,In this paper, C is given as the spring constant, as obtained from equation 4;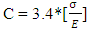 | (4) |
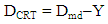 | (5) |
2.2. Computation of Variables
- The variables were computed on spreadsheet shown in figure 1 to generate values for the desired spring diameter (Dmd) and the air gap created due to spring-back effect (Y).
 | Figure 1. Spreadsheet for generating data for determining the relationship between “Air-gap, Y” and “Desired Spring Diameter, Dmd for varying wire thickness (Dw) of tungsten |
3. Result and Discussion
- Graphs (figures 2-7) were plotted for different thickness to observe the extent to which increase in mandrel diameter affects the air-gap created due to spring-back effect considering tungsten wire.
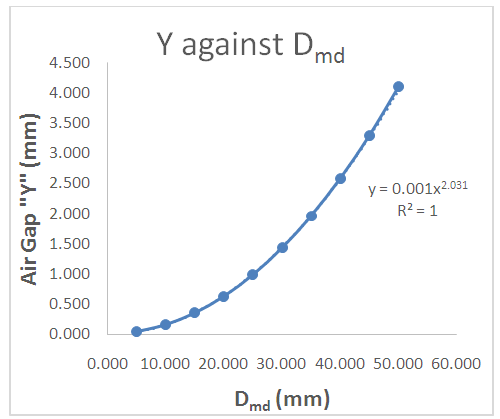 | Figure 2. Plot of Air Gap “Y’ against Desired Spring Diameter “Dmd” for tungsten wire of 1.5mm thickness |
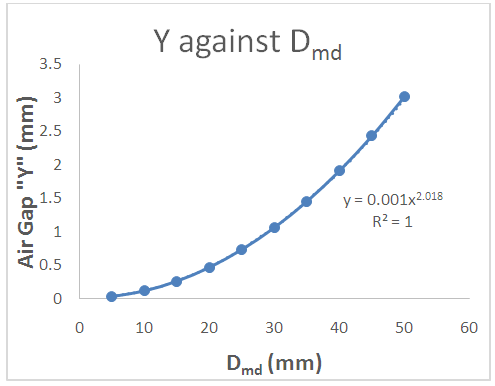 | Figure 3. Plot of Air Gap “Y’ against Desired Spring Diameter “Dmd” for tungsten wire of 2.0mm thickness |
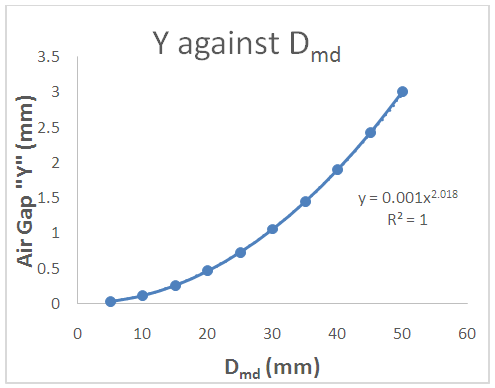 | Figure 4. Plot of Air Gap “Y’ against Desired Spring Diameter “Dmd” for tungsten wire of 2.0mm thickness |
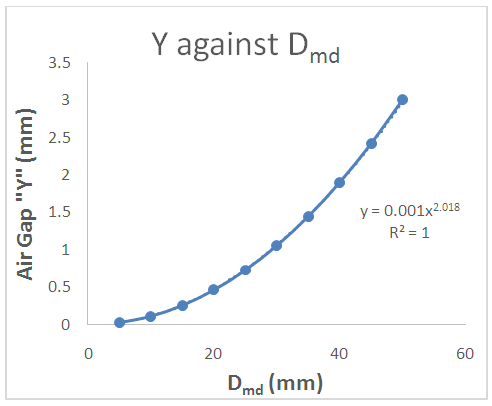 | Figure 5. Plot of Air Gap “Y” against Desired Spring Diameter “Dmd” for tungsten wire of 3.0mm thickness |
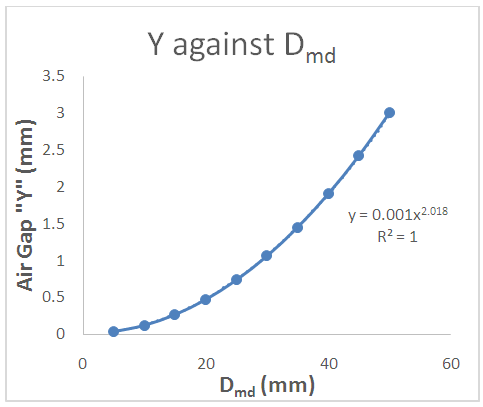 | Figure 6. Plot of Air Gap “Y” against Desired Spring Diameter “Dmd” for tungsten wire of 3.5mm thickness |
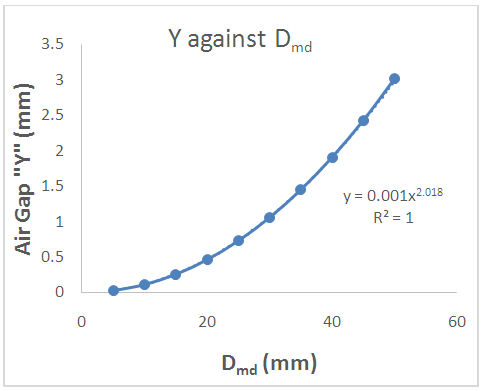 | Figure 7. Plot of Air Gap “Y” against Desired Spring Diameter “Dmd” for tungsten wire of 4.0mm thickness |
4. Conclusions
- Conclusively, the work has shown dependence of air-gap on the size of the mandrel, that is the higher the mandrel diameter, the higher the value of the air-gap. Hence, the diameter of the mandrel to be used in making a spring of a particular diameter can be determined by subtracting the value of the air-gap obtained from the desired diameter of a spring. Also, the spreadsheet caters for tungsten wire of thickness less than 10mm, hence if the desired radius and thickness are known, the mandrel size to be used can be generated from the sheet. Also, from figures 2-7 we can conclude that tungsten material behaves the same way irrespective of thickness when used for spring.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML