1. Introduction

To say everything happens in a space-time is very, very trivial. But what is this space-time? Or more precisely, how can this space-time be described? What mathematical structure best describes space-time? And from this mathematical structure, what consequences can we deduce that correspond to experimentally-discovered facts?

In both classic physics and common sense, space-time is a four-dimensional Euclidean space with:

1. three spatial dimensions represented by real numbers, with three axes orthogonal to each other

2. a temporal axis represented by real numbers.

It's assumed this space-time is independent from the observer; or, rather, measures of space and time intervals do not depend on the observer, and in particular their speed. Overall, it is assumed space and time are independent of each other. The measure of time intervals is the same wherever I am.

As everyone knows, relativistic theories and especially relativistic quantum mechanics don't use this model of space-time because it fails to describe many phenomena. These theories utilize a model in which measures of space and temporal distances depend upon the observer. In general relativity, curvature, an important feature of space-time, is deeply influenced by mass-energy density.

In many attempts to create an "everything theory," more exotic space-times have been used. Instead of four dimensions, twelve or more have been employed [1]. In other theories, space-time is quantized [2]. It is not described by real numbers but by integers or natural numbers.

This paper is not about these theories. The author is not a theoretical physicist. Nevertheless it will be shown that, starting from a quantized time and from some experimental facts (or rather from a series of assumptions which will be taken as experimental facts), several things can be demonstrated. And these things are very, very important features of the world in which we live and which current theories take for granted.

2. Time Quantized: What Happens?

Let us suppose time is quantized or, more precisely, every measure of time coordinates will yield an integer that is a multiple of a fundamental unit we will indicate as Tfond. Obviously, every measure of a time interval will be the result of:

n*Tfond

with n a natural number different from 0. The first thing we can say (with the important consequence in boldface) is:

First consequence: space must be quantized too

We can take as an experimental fact the relativistic affirmation that space and time aren't separate but are a unique entity—space-time. In a more formal way we can start from the fourth Lorentz transformation connecting time and space coordinates. Then it's impossible to have time with integer values and space coordinates given in real numbers. We will then have an Sfond minimal unit of space. Obviously if time and space are both quantized speed and acceleration are quantized too because quantum mechanics and relativistic theories modify but don't contradict the classical definition of speed and acceleration as space-time ratios. The only difference is that speed and acceleration are given in rational numbers and not integers.

Another very important consequence will be:

Second consequence: space-time cannot be Euclidean

This affirmation is a stronger general relativity affirmation because this theory affirms that space-time has a variable structure (a metric tensor) depending on mass-energy density (an impulse-energy tensor). Then in some cases, space-time can be Euclidean. To understood why quantized space-time cannot be Euclidean, let us consider a Cartesian plane (see figure below) in which we consider only those points having integer coordinates. We want to build a geometry with these points.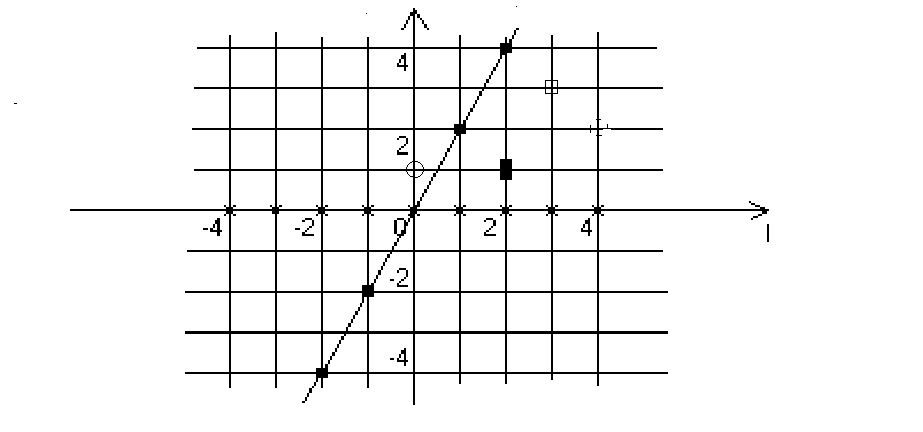

Figure 1. Example of a quantized plane

It's always possible to define a straight line as an assembly of points such that, taking any two points, the ratio between the difference of their y coordinates and the difference of their x coordinates is constant. From this, let us see what happens to the postulates of Euclidean geometry:

1. First postulate (for every couple of points there is one and only one straight line connecting them) is always true.

2. Second postulate (for every straight line there are points not belonging to it) is always true.

3. Third or continuity postulate. Every straight line is an ordinate ensemble of points such that before and after one generic point there are infinite points and such that between two generic points there are infinite points. This postulate is false because between points whose coordinates differ by 1 there is no other point.

4. Fourth postulate. Every straight line is equal. The author doesn't known if this postulate is still valid.

5. Fifth or parallel straight lines postulate. Given a straight line r and one point there is one and only one straight line parallel to r passing through the point. This is not true. Looking back at Figure 1, notice that for the point at coordinate 2,1 (the filled black rectangle) there are at least two straight lines not having points in common with the straight line shown in the figure. These straight lines are: the one connecting point 2,1 with point 0,1 (hollow circle) and that connecting point 2,1 with point 4,3 (hollow rectangle).

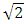There is an important remark that must be made. Anyone can see that the model used is a bad approximation of "real" quantized space. Indeed, if we examine the figure more closely, we see that the distance from any two generic points can be times S_fond, and that this number is not an integer multiple of S_fond. The observation is correct but, as can be seen in more specialized texts, discrete spaces cannot be Euclidean because of profound differences in the definition of the metric [3].

Let us take an uncertain time-energy principle of the form

Δt*ΔE≥ħ

as an experimental conclusion deduced by the study of particle physics. Let us further admit there are quantum states in which this relation applies as an equivalence. It's evident by time quantization that we derive:

Third consequence: energy in any form is quantized

The only difference will be energy will not be given as a multiple of a fundamental unit but as

ΔE=(1/n)*(1/Tfond)

Now let take the mass-energy equivalence as an experimental fact derived by studies of nuclear reactions. Rest mass has to be quantized too. And so does impulse. This is not only evident, but it also leads to a fourth and fifth consequence:

Fourth consequence: energy cannot be equal to 0; it must be a not-vanishing zero-point

Fifth consequence: there is a maximum value for energy too. It is when n=1. The same is true for impulse

Let us call this "maximum value of energy" the highest possible energy. Now let us pause for thought. A not vanishing zero-point energy is predicted by quantum mechanics, but it seems to contradict the evidence [4] that the universe's total energy is almost zero. But this contradiction is only apparent: if one examines the previous formula, one sees that, while energy cannot be exactly zero, for arbitrarily great values of n it can indeed assume very small values.

This quantization of any form of energy would seem to contradict some results of quantum mechanics. The first contradiction is that the energy spectrum of a free particle is continuous. This result derives from the resolution of the Schrödinger and Dirac equations. But if we consider a finite sized universe (including not only the universe in which we live, but everything that can be observed, including multi-universes) then it's evident that a free particle cannot exist. There can only be a particle in a box (albeit a universe-sized box), and that the energy spectrum of this particles is quantized. It then appears that the universe must have a finite size. Moreover, if energy cannot exceed a maximum value, then it's difficult to think of an infinite Universe; otherwise, its total energy would also be infinite.

The second result is this: Quantum theories predict energy quantization in many cases (from harmonic oscillation of atoms from energetic levels of molecules to field values and so on), but these energy quantizations, or more specifically their rules, are case dependent. In our case there is only a rule of quantization that we call "our case quantization." But this contrast is only apparent.

To explain, let us consider two successive energy levels of a harmonic oscillator. Their difference is much lower than the highest possible energy of our case—tens of orders of magnitude lower. So we have the case in which the difference between n and n+1 energy levels of "our case quantization" is absolutely negligible with respect to a difference of energy between consecutive levels of a quantum system as the harmonic oscillator.

So if an energy level required by quantum theories is not equal to that provided by our rule, the difference is so small as to escape experimental measurement. Instead, the detection of this difference could turn into a test of the quantization of time as well as the observation of the Lamb shift as a test of Quantum Electrodynamics.

If time is quantized, then the frequency of every periodic phenomenon is quantized too. Then if there is some case where energy is proportional to frequency, then in this case energy is surely quantized.

Let us go on. If energy and rest mass are quantized, then impulse p has to be quantized too. Let take as an experimental fact Heisenberg's uncertainty principle, which is

Δp*Δx≥ħ

and take this relation as an equivalence (and we know there are quantum states in which this happens). We find (again!) that space is quantized. Not only that, but because Δp cannot be zero, Δx cannot be greater than a certain value. And so we find, again,

Sixth consequence: the universe has to have a finite size

On the other side of the coin, space quantized means that no object can have zero dimensions. The Big Bang Theory has to be improved because

Seventh consequence: an initial singularity cannot exist

And it's a very useful consequence because it eliminates every problem that singularity creates.

Last but not least, if there is a minimum value for time and the universe has a finite size, then

Eighth consequence: an ultimate speed must exist

…as the speed to cross the whole universe in a time equal to Tfond. This speed is greater, much greater, than the speed of light. Tachyons can be in a quantized space-time, but there must be an ultimate speed. A link can be hypothesized between this ultimate speed and light speed.

To conclude, let us remember two things:

1. Angular momentum, related to energy, has to be quantized too. But as Dirac demonstrated in the 1930's [5], if angular momentum is quantized and there is, or has been, only one magnetic monopole, then electrical charge has to be quantized too.

2. Secondly, it has been recently proposed [6] that, from a discrete space-time, a "dark energy" arises in spontaneous way.

And with the aim of this paper satisfied, we can stop here.

3. Conclusions

Let try to associate some numbers to Tfond and other quanta. We are in MKS. Now it's clear Tfond and Sfond have to be much less than every time and space measured. And the maximum possible energy has to be much greater than every measured energy. Now let us take maximum measured energy to be [7]:

10^-52*c² Joule practically 10^-70

From the energy-time uncertainty principle we have a Tfond of less than 10^-100 second—a very brief time indeed! And by calculations that aren't reported here, a value of 10^-70 meters is obtained by Sfond.

With these small values and some simple calculus it's evident that the energy of both the quantum and macroscopic systems has to be linked to a number n much higher than we have considered for energy quantization. With such small values it would be impossible to detect the quantum nature of space-time. And clearly the assumptions for this paper have been oversimplified. However it's impressive that, with only one hypothesis and some experimental facts, one can derive consequences of such importance. A non-Euclidian space-time quantization of every form of energy, a universe of finite size, the necessity of an ultimate speed, a not vanishing zero-point energy, the non-existence of an initial singularity, and perhaps the existence of a "dark energy"—every important thing that the standard model is unable to forecast but not contradicting the experimental facts.

Consequences have to be predicted and, in some cases, are predicted by theories aiming to be the "Everything theory."

It's evident that, if a theory of quantized space-time is built in a more precise and formal way, many features of the universe in which we live could be explained. This is the most important aim of the "Everything theory."