-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2013; 3(3): 81-88
doi:10.5923/j.fs.20130303.01
The Higgs-like Bosons and Quark Compositeness
Mario Everaldo de Souza
Departamento de Física, Universidade Federal de Sergipe, São Cristovão, 49100-000, Brazil
Correspondence to: Mario Everaldo de Souza, Departamento de Física, Universidade Federal de Sergipe, São Cristovão, 49100-000, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Considering that each quark is composed of two prequarks, called primons, it is shown that the recently found neutral Higgs-like boson belongs to a triplet constituted of a neutral boson 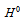 and two charged bosons
and two charged bosons 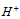 and
and 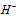 , and that
, and that 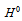 is, actually, a triplet and both
is, actually, a triplet and both 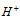 and
and 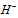 are doublets. The quantum numbers of these bosons are calculated and shown to be associated to a new kind of hypercharge which is directly related to the weak decays of hadrons and to the CKM matrix elements. Solutions to the proton spin puzzle and to other problems of particle physics are presented.
are doublets. The quantum numbers of these bosons are calculated and shown to be associated to a new kind of hypercharge which is directly related to the weak decays of hadrons and to the CKM matrix elements. Solutions to the proton spin puzzle and to other problems of particle physics are presented.
Keywords: Higgs Boson, Higgs-like Bosons, CKM Matrix, Weak Decays, Preons, Prequarks, Primons
Cite this paper: Mario Everaldo de Souza, The Higgs-like Bosons and Quark Compositeness, Frontiers in Science, Vol. 3 No. 3, 2013, pp. 81-88. doi: 10.5923/j.fs.20130303.01.
Article Outline
1. Introduction
- The collaborations ATLAS[1,2] and CMS[3] have recently discovered a light narrow resonance around 126 GeV. This remarkable discovery, supported by evidence from the Tevatron[4], has triggered discussions on the nature of such resonance because both ATLAS and CMS report discrepancies with respect to the Standard Model (SM) backgrounds. The data have established that it is indeed a boson, probably neutral with spin zero. The identification of the new resonance with the long-sought Higgs boson of the Standard Model is not certain at all. In particular, D0 and CDF have reported an excess of the top quark forward-backward asymmetry
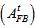 [5,6] and an enhancement in the
[5,6] and an enhancement in the  channel[4], while the LHC has reported an excess in the diphoton channel[7,8]. These disagreements in the Higgs couplings, as pointed out by Choudhury et al.[9], is “a Window to New Physics”. Because of this possibility there has lately been an array of different proposals offering alternatives for new physics and treating the newly found resonance as a Higgs-like boson. There are many recent references in this line such as, for example, the eight references[10,11,12,13,14, 15,16,17]. One sees that there are works proposing Higgs doublets and Higgs triplets. In particular, Low, Lykken & Shaughnessy[17] propose that the newly found boson is the neutral member of an electroweak triplet of a custodial 5-plet. This work presents a different view from all the works above mentioned and brings to the discussion the possibility of a composite quark. Although prequarks (or preons) have not yet been directly proven by any experiment, there are several indirect evidences of their existence. Some examples are: 1) the distributions of charge in nucleons, found by Hofstadter & Herman[18] that cannot be explained by three point-like quarks; 2) the ad hoc Kobayashi-Maskawa matrix elements; 3) the so-called EMC effect[19,20] according to which quarks of nucleons are slower when nucleons are inside nuclei; 4) the SLAC E143 Collaboration[21], the Spin Muon Collaboration[22] and Hermes Collaboration[23] have found that the three quarks of the proton account for only half of its total spin which is a fact called the proton spin puzzle; 5) G. Miller at Argonne[24] found that close to its center the neutron has a negative charge equal to -1/3e (inside the positive region with +1/2e). Another important effect was discovered by the group of Prof. Alan Krisch that conducted the interaction of a polarized proton beam on a polarized proton target. The data show[25] that, when the collision intensity is higher, protons with parallel spins interact much stronger than protons with anti-parallel spins. According to QCD both cases would have the same strength. Let us recall that according to QCD’s asymptotic freedom the forces between quarks become weaker at short distances.My argumentation is that QCD is not wrong. It cannot explain the Krisch effect because it is due to the substructure of quarks. I present in section 7 an explanation for this effect and for the other ones above mentioned. Commenting on the discovery of quarks at SLAC, M. Riordan[26] says “A way to interpret this unexpected behavior was that the electrons were hitting some kind of hard core inside the target protons”. Taking into account the quark model of today we know that such core was not made of quarks. Later on, below, we will grasp the true nature of this core. Ending the introduction I can say that preons have not yet been directly found by the LHC because they should be very light fermions and, thus, they are very hard to be directly seen, and thus with the LHC energies we only see the bosons related to their interaction. As it will be shown below there should exist a neutral boson (already found by the LHC) and two charged bosons (yet to be found).
channel[4], while the LHC has reported an excess in the diphoton channel[7,8]. These disagreements in the Higgs couplings, as pointed out by Choudhury et al.[9], is “a Window to New Physics”. Because of this possibility there has lately been an array of different proposals offering alternatives for new physics and treating the newly found resonance as a Higgs-like boson. There are many recent references in this line such as, for example, the eight references[10,11,12,13,14, 15,16,17]. One sees that there are works proposing Higgs doublets and Higgs triplets. In particular, Low, Lykken & Shaughnessy[17] propose that the newly found boson is the neutral member of an electroweak triplet of a custodial 5-plet. This work presents a different view from all the works above mentioned and brings to the discussion the possibility of a composite quark. Although prequarks (or preons) have not yet been directly proven by any experiment, there are several indirect evidences of their existence. Some examples are: 1) the distributions of charge in nucleons, found by Hofstadter & Herman[18] that cannot be explained by three point-like quarks; 2) the ad hoc Kobayashi-Maskawa matrix elements; 3) the so-called EMC effect[19,20] according to which quarks of nucleons are slower when nucleons are inside nuclei; 4) the SLAC E143 Collaboration[21], the Spin Muon Collaboration[22] and Hermes Collaboration[23] have found that the three quarks of the proton account for only half of its total spin which is a fact called the proton spin puzzle; 5) G. Miller at Argonne[24] found that close to its center the neutron has a negative charge equal to -1/3e (inside the positive region with +1/2e). Another important effect was discovered by the group of Prof. Alan Krisch that conducted the interaction of a polarized proton beam on a polarized proton target. The data show[25] that, when the collision intensity is higher, protons with parallel spins interact much stronger than protons with anti-parallel spins. According to QCD both cases would have the same strength. Let us recall that according to QCD’s asymptotic freedom the forces between quarks become weaker at short distances.My argumentation is that QCD is not wrong. It cannot explain the Krisch effect because it is due to the substructure of quarks. I present in section 7 an explanation for this effect and for the other ones above mentioned. Commenting on the discovery of quarks at SLAC, M. Riordan[26] says “A way to interpret this unexpected behavior was that the electrons were hitting some kind of hard core inside the target protons”. Taking into account the quark model of today we know that such core was not made of quarks. Later on, below, we will grasp the true nature of this core. Ending the introduction I can say that preons have not yet been directly found by the LHC because they should be very light fermions and, thus, they are very hard to be directly seen, and thus with the LHC energies we only see the bosons related to their interaction. As it will be shown below there should exist a neutral boson (already found by the LHC) and two charged bosons (yet to be found).2. The Quark Compositeness Model
- Quark compositeness is an old idea, proposed since the 1970s[27-37]. In order to distinguish the model of this work from the other models found in the literature above cited I name the prequarks of this model with a different name: primons. Primon is a word derived from the Latin word primus which means first. A major distinction is that in this work leptons are supposed to be elementary particles. This is actually consistent with the smallness of the electron mass which is already too small for a particle with a very small radius[38]. Another important distinction is that this work breaks the quark into two particles instead of three particles. Some major parts of the model have been presented in references[39,40].
2.1. Compositeness of Quarks Flavors and Colors
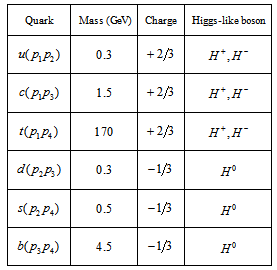
- In order to reproduce the spectrum of 6 quarks and their colors we need 4 primons (
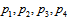 ) in 3 supercolor states
) in 3 supercolor states 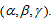 Each color is formed by the two supercolors of the two primons forming a particular quark (Table 1). As to charge, primons have charges +(5/6)e and (-1/6)e according to Table 2. With this construction of quarks flavors we solve one of the problems of particle physics: there are only six quarks. Of course, there is a similar construction for the antiquarks (with antiprimons). Using Table 2 we obtain Table 3 for the flavors of quarks.
Each color is formed by the two supercolors of the two primons forming a particular quark (Table 1). As to charge, primons have charges +(5/6)e and (-1/6)e according to Table 2. With this construction of quarks flavors we solve one of the problems of particle physics: there are only six quarks. Of course, there is a similar construction for the antiquarks (with antiprimons). Using Table 2 we obtain Table 3 for the flavors of quarks.
|
|
|
2.2. The New Hypercharge and the New SU(2)
- For primons we should have the baryon number B=1/6, of course. As it is described in references[39,40], going on the footsteps of Gell-Mann and Nishijima (for the quark model), we can use the formulas
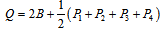 | (1) |
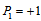 , for primon
, for primon 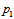 , and
, and 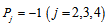 for the other primons. Thus, we have
for the other primons. Thus, we have  | (2) |
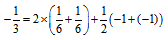 | (3) |
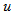 and
and  have isospins equal to
have isospins equal to 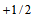 and
and 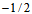 , respectively, we are forced to have
, respectively, we are forced to have 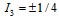 for primons,
for primons, 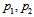 and
and  Making use of the modified Gell-Mann—Nishijima relation
Making use of the modified Gell-Mann—Nishijima relation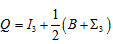 | (4) |
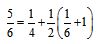 | (5) |
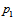 , and
, and 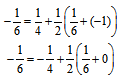 | (6) |
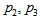 and
and  Therefore,
Therefore, 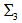 can assume the values
can assume the values  and
and  and, thus, these values can be considered as the projections of
and, thus, these values can be considered as the projections of  (Table 4).In terms of
(Table 4).In terms of 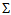 and
and 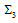 a quark has the four possible states
a quark has the four possible states  (described in detail in ref.[39,40]):
(described in detail in ref.[39,40]):
|
 are written as
are written as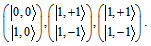 Organizing the values of
Organizing the values of 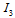 and
and 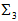 for quarks on a table we obtain Table 5 below.
for quarks on a table we obtain Table 5 below.
|
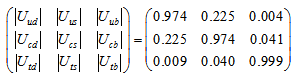 we notice that the matrix elements
we notice that the matrix elements 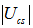 and
and 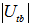 , which are about 1, satisfy the selection rule
, which are about 1, satisfy the selection rule  ,
, 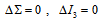 . The other very large element
. The other very large element 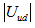 (which is also close to 1) satisfies the selection rule
(which is also close to 1) satisfies the selection rule 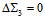 ,
,  . From these three matrix elements we obtain the rule: The largest elements have either the maximum
. From these three matrix elements we obtain the rule: The largest elements have either the maximum 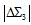 or the maximum
or the maximum  within the same quark doublet. The other large elements
within the same quark doublet. The other large elements 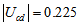 and
and 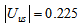 obey, respectively, the selection rule
obey, respectively, the selection rule 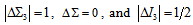 . From the diagram we see why
. From the diagram we see why 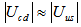 . According to the diagram we should have
. According to the diagram we should have 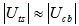 and
and 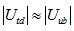 and this is indeed the case. Therefore, the CKM matrix elements are directly related to the substructure of quarks. Let us recall that within the Standard Model the CKM matrix is an ad hoc element.
and this is indeed the case. Therefore, the CKM matrix elements are directly related to the substructure of quarks. Let us recall that within the Standard Model the CKM matrix is an ad hoc element. | Figure 1. Diagram showing how weak decays are related to the variations of 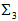 and and  |
3. The Weak Decays of Hadrons
- Taking into account the values of the new quantum numbers
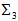 for quarks, de Souza[42] has shown that the weak decays of all hadrons (leptonic, semileptonic and nonleptonic) are directly related to the variations of
for quarks, de Souza[42] has shown that the weak decays of all hadrons (leptonic, semileptonic and nonleptonic) are directly related to the variations of  , that is, to
, that is, to  and, thus, there is a vectorial current
and, thus, there is a vectorial current 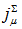 between quarks. As an example, I present on Table 6 the semileptonic decays of light baryons.
between quarks. As an example, I present on Table 6 the semileptonic decays of light baryons.4. The Masses of Primons
- The magnetic moments of primons should be given by
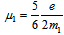 for
for 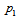 and
and 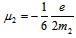 for
for 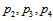 and, hence
and, hence 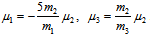 . Since the spin content of quarks should be the same we have
. Since the spin content of quarks should be the same we have | (7) |
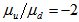 , and using the above relations we obtain
, and using the above relations we obtain | (8) |
 and solving for the ratio
and solving for the ratio 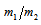 we arrive at
we arrive at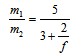 | (9) |
|
 and
and  are approximately equal, it is reasonable to consider
are approximately equal, it is reasonable to consider 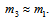 Supposing that
Supposing that 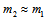 , we obtain
, we obtain 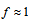 which is very consistent. Therefore, primons should have approximately the same mass which is an inherent mass such as that of leptons.
which is very consistent. Therefore, primons should have approximately the same mass which is an inherent mass such as that of leptons.5. The Arrangement of Primons in the Nucleons and the Stability of the Proton
5.1. The Arrangement of Primons in the Nucleons
- Taking into account the results of Hofstadter & Hermann[18] on the charges of the nucleons we can say that both nucleons should have an inner common central core constituted of primons
 . The outer primons of the proton are
. The outer primons of the proton are  according to Fig. 2 below. The outer primons of the neutron are
according to Fig. 2 below. The outer primons of the neutron are 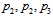 , forming quarks
, forming quarks 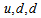 between the two layers. It is worth mentioning that this picture of the nucleons completely agrees with the results of Miller[24] who found a charge of
between the two layers. It is worth mentioning that this picture of the nucleons completely agrees with the results of Miller[24] who found a charge of 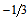 inside the central positive core of the neutron. This
inside the central positive core of the neutron. This 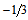 charge is the result of
charge is the result of 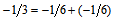 of primons
of primons  and
and 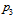 . This picture of the nucleons also completely agrees with the results of Povn and Hüfner[43] that have found an average size of about 0.5 fm for constituent quarks
. This picture of the nucleons also completely agrees with the results of Povn and Hüfner[43] that have found an average size of about 0.5 fm for constituent quarks 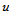 and
and  .
. | Figure 2. Pictorial representation of the arrangement of primons in the proton |
5.2. The Stability of the Free Proton
- Taking into account the stability of the (free) proton we can deduce that
 and
and 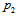 should be stable against weak decay. What about
should be stable against weak decay. What about 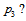 From the instability of the free neutron we deduce that
From the instability of the free neutron we deduce that  should suffer weak decay, but only the outermost
should suffer weak decay, but only the outermost  because the innermost
because the innermost 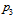 is also present in the proton. We can understand why this happens taking a look at the decays of hadrons and observing that weak decays do not occur when both
is also present in the proton. We can understand why this happens taking a look at the decays of hadrons and observing that weak decays do not occur when both 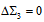 and
and 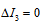 .Let us recall that
.Let us recall that 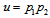 so that
so that 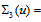
 , and that
, and that 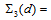
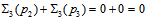 . As to
. As to 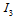 we have that
we have that 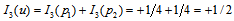 , and
, and 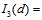
 . Therefore, the inner layer of the proton (
. Therefore, the inner layer of the proton (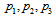 ) has
) has 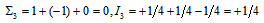 because the
because the 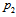 of the inner layer belongs to
of the inner layer belongs to 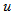 . In the outer layer (
. In the outer layer ( ) the first
) the first 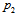 belongs to
belongs to  and the other one belongs to
and the other one belongs to  , so that
, so that 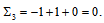 As to
As to 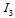 we have
we have 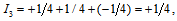 and thus
and thus 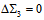 ,
, 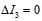 between the two layers. Therefore, the free proton is always stable. For the neutron the inner layer is the same as in the proton, and the outer layer
between the two layers. Therefore, the free proton is always stable. For the neutron the inner layer is the same as in the proton, and the outer layer 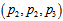 has
has 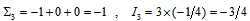 , and thus between the innermost and outermost layers
, and thus between the innermost and outermost layers 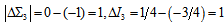 , and thus, the free neutron always decays.
, and thus, the free neutron always decays.6. The Higgs-like Bosons and their Quantum Numbers
6.1. The Spins of Primons and of the Higgs-like Bosons
- In order to have
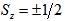 for quarks, we should have
for quarks, we should have 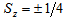 for primons. Thus, we postulate that primons are fermions
for primons. Thus, we postulate that primons are fermions 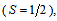 but with
but with 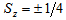 . Taking a look at Fig. 2 each layer of primons should have
. Taking a look at Fig. 2 each layer of primons should have  , so that the two layers together should always have
, so that the two layers together should always have  , of course. Therefore, the Higgs-like bosons should have
, of course. Therefore, the Higgs-like bosons should have 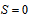 , and are, thus, scalar bosons. On subsection 7.3 on the solution of the Proton Spin Puzzle we return to discuss the spins of primons.
, and are, thus, scalar bosons. On subsection 7.3 on the solution of the Proton Spin Puzzle we return to discuss the spins of primons.6.2. The Quantum Numbers  of the Higgs-like Bosons
of the Higgs-like Bosons
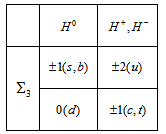
- Taking into account the charges of primons from Table 2, we see that there should be three Higgs-like bosons,
 for generating the masses of quarks as it is shown on Table 7, because
for generating the masses of quarks as it is shown on Table 7, because  Let us now assign the quatum numbers
Let us now assign the quatum numbers 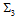 for the Higgs-like bosons. As
for the Higgs-like bosons. As 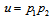 , its
, its 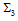 is
is  , and so we have
, and so we have 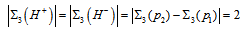 . For
. For 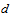 we have
we have 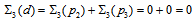 , and thus,
, and thus,  . Doing the same for the other quarks, and summarizing the results on a table, we obtain Table 8 below.
. Doing the same for the other quarks, and summarizing the results on a table, we obtain Table 8 below.
|
6.3. The Masses of the Higgs-like Bosons
- The mass of
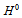 has been measured by the collaborations ATLAS[1,2] and CMS[3] as being about 126 GeV. This corresponds to a Compton wavelength around
has been measured by the collaborations ATLAS[1,2] and CMS[3] as being about 126 GeV. This corresponds to a Compton wavelength around  m. It is important to point out that the mass of
m. It is important to point out that the mass of 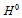 is of the same order of that of the weak boson
is of the same order of that of the weak boson 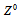 . The charged weak bosons
. The charged weak bosons 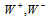 have a mass
have a mass 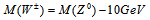 . I think it is not purely coincidental that the mass of
. I think it is not purely coincidental that the mass of 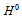 and of the weak bosons have the same order of magnitude. From this we may guess that the mass of
and of the weak bosons have the same order of magnitude. From this we may guess that the mass of  and
and 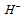 is
is  .
.
|
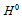 which probably have 2 slightly different masses, that is, the
which probably have 2 slightly different masses, that is, the  s with
s with  may have a different mass from the
may have a different mass from the 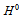 with
with  . In fact, CMS and ATLAS have reported for the Higgs boson the respective masses of
. In fact, CMS and ATLAS have reported for the Higgs boson the respective masses of 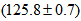 GeV and
GeV and 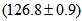 GeV[44] which may be the two different masses above mentioned. The same may hold for the charged bosons. The
GeV[44] which may be the two different masses above mentioned. The same may hold for the charged bosons. The  with
with 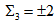 and the
and the  with
with 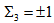 may have slightly different masses. The
may have slightly different masses. The 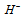 bosons, of course, should have the same behavior.
bosons, of course, should have the same behavior.7. The Higgs-like Lagrangian
- In order to construct a gauge theory for this new interaction we should consider a Lagrangian for three massive spin-0 bosons, of the type
 | (10) |
 refer to the three Higgs-like fields corresponding to
refer to the three Higgs-like fields corresponding to 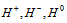 , respectively, with their corresponding masses
, respectively, with their corresponding masses 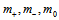 . This is a well known Lagrangian found in the literature which satisfies Klein-Gordon equation. For example, in reference[45] there is a detailed discussion on this subject. We just have to consider that, according to what was above discussed, we have a
. This is a well known Lagrangian found in the literature which satisfies Klein-Gordon equation. For example, in reference[45] there is a detailed discussion on this subject. We just have to consider that, according to what was above discussed, we have a 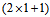 -dimensional
-dimensional 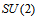 directly linked to
directly linked to  . That is, there are the
. That is, there are the 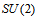 bosonic current
bosonic current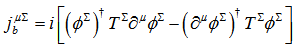 | (11) |
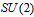 fermionic current
fermionic current | (12) |
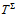 are matrices of the
are matrices of the 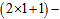 dimensional representation of
dimensional representation of  Therefore, we should modify the Standard Model replacing the Higgs field Lagrangian by the above Higgs-like field Lagrangian. For the interaction between the two primons that form a particular quark the Lagrangian is much more complex. One of the complications comes from the fact of having
Therefore, we should modify the Standard Model replacing the Higgs field Lagrangian by the above Higgs-like field Lagrangian. For the interaction between the two primons that form a particular quark the Lagrangian is much more complex. One of the complications comes from the fact of having 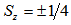 for each primon. Since Dirac equation has the Pauli spin matrices included inside the
for each primon. Since Dirac equation has the Pauli spin matrices included inside the 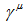 matrices, we should have a modified Dirac equation for primons. Another complication comes from the fact that the spins of the primons of a quark should change together when, for example, a quark interacts with a gluon since gluons have spin 1. This means that for a pair of primons forming a quark
matrices, we should have a modified Dirac equation for primons. Another complication comes from the fact that the spins of the primons of a quark should change together when, for example, a quark interacts with a gluon since gluons have spin 1. This means that for a pair of primons forming a quark 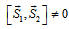 and thus the spin degrees of freedom are not independent from each other. This leads to some interesting properties regarding the nucleon as a whole as discussed in reference[39].Thus, the Lagrangians of the two primons that form a quark have to be coupled. We should investigate this matter much further.
and thus the spin degrees of freedom are not independent from each other. This leads to some interesting properties regarding the nucleon as a whole as discussed in reference[39].Thus, the Lagrangians of the two primons that form a quark have to be coupled. We should investigate this matter much further.8. Solutions to Some Important Problems of Particle Physics
8.1. The Electric Charge Densities in the Nucleons
- The results of the experiment of Hofstadter & Hermann are the starting point for the model. We notice that there is a complete coherence between the experimental results and the model. And moreover, the model completely agrees with the findings of Miller[24] according to whom there is a negative charge of
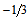 inside the positive central part of the charge density of the neutron. Neither result can be accounted for by three point-like quarks.
inside the positive central part of the charge density of the neutron. Neither result can be accounted for by three point-like quarks.8.2. The Number of Quarks
- The 4 primons arranged in pairs with different flavours form exactly 6 quarks.
8.3. The Proton Spin Puzzle
- As it was shown by de Souza in references[40] and[42], the puzzle is easily solved. Here we just mention the main points. Deep Inelastic Scattering (DIS) experiments have probed the inner layer of primons of the proton, and that is why the results yield about half of the total spin. Taking into account the other layer of primons we arrive at a total spin
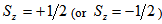 as it should be.
as it should be.8.4. The CKM Matrix Elements and Cabibbo Factors
- The results of section 2.2 above and the results of reference[42] clearly pave the way for the understanding of the CKM matrix elements which are presently completely ad hoc. They are directly related to the variations of
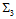 in weak decays. As it is seen in reference[42] Cabibbo factors are also directly related to the variations of
in weak decays. As it is seen in reference[42] Cabibbo factors are also directly related to the variations of 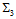 in weak decays.
in weak decays.8.5. The Dual Roles of Quarks: Valence and Constituent Quarks
- Valence quarks are, actually, primons, and are almost massless, and constituent quarks are the true quarks. Thus, there is a confusion in the interpretation of the data. The three outermost primons have not yet been directly seen because they become blurred into the quark sea in deep inelastic scattering experiments and only the three innermost primons have been seen together as an inner core and two of them have been seen together according to G. Miller findings (my interpretation). This is the same inner core that was seen by Hofstadter & Hermann and was also reported by M. Riordan[26] on the description of the discovery of quarks. This subject is discussed in more detail in references[40] and[42].
8.6. The EMC Effect
- The EMC effect is due to the interactions between primons of the outermost layer of a nucleon and primons of the outermost layer of another close nucleon. That is, there should be something like primon bonds between two close nucleons. The model opens up the possibility for the understanding of the hole inside the alpha particle and its point group symmetry which is
 [46], that is, it has a pyramidal shape. With point-like quarks we will never understand how such arragement of nucleons such as the deuteron and the alpha particle can be formed.
[46], that is, it has a pyramidal shape. With point-like quarks we will never understand how such arragement of nucleons such as the deuteron and the alpha particle can be formed.8.7. The Krisch Effect
- As it was shown in the introduction, Prof. Alan Krisch group conducted the interaction of a polarized proton beam on a polarized proton target and found[25] that, at higher collision intensities, protons with parallel spins interact stronger than protons with anti-parallel spins. At very high energies, most interactions arise from the interactions between the two central layers of primons of the two protons, that is, between the set
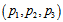 of a proton and the set
of a proton and the set  of the other proton. When the two protons have parallel spins, in terms of spins we have for each central layer of primons two spins up and one spin down (or the other way around) and, thus, there are, 04 interaction with
of the other proton. When the two protons have parallel spins, in terms of spins we have for each central layer of primons two spins up and one spin down (or the other way around) and, thus, there are, 04 interaction with 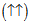 and 01 with
and 01 with  (for two spins up, and one spin down) because the Higgs-like bosons have . When the proton spins are antiparallel we have two spins up and one spin down for one proton, and two spins down and one spin up for the other proton (or the other way around). In this case we have 02 interactions with
(for two spins up, and one spin down) because the Higgs-like bosons have . When the proton spins are antiparallel we have two spins up and one spin down for one proton, and two spins down and one spin up for the other proton (or the other way around). In this case we have 02 interactions with 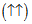 and 02 interaction with
and 02 interaction with 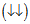 . Therefore, there is a ratio of
. Therefore, there is a ratio of 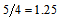 between the two cases. That is, there are about 11.12% more transitions for parallel protons than for antiparallel protons.
between the two cases. That is, there are about 11.12% more transitions for parallel protons than for antiparallel protons.8.8. The Masses of Baryons and the Harmonic Approximation for Effective Potentials
- Taking a look at Fig. 2 we observe that when protons collide at high energies and form baryon resonances, the quarks oscillate quite a lot and can be considered as quantum oscillators. That is why de Souza[47] was able to describe the masses of almost all baryons using such an approximation. The first excited state of
 , which had been predicted to have a mass of 5.93 GeV, has recently been reported[48] by CDF with a mass of about 5.92 GeV, just 0.17% off.
, which had been predicted to have a mass of 5.93 GeV, has recently been reported[48] by CDF with a mass of about 5.92 GeV, just 0.17% off.9. Conclusions
- I have presented a completely new view for the Higgs-like bosons in terms of a substructure for quarks. It is a very coherent model, based on experimental data. The quantum numbers of the Higgs-like bosons are presented and are directly related to the weak decays of hadrons. Solutions have been presented to some important problems of the Physics of hadrons and quarks. It is a model that can be tested further with more data from the LHC.
ACKNOWLEDGEMENTS
- I would like to thank Felipe Reis Machado da Silva from PDDesign from Universidade Federal de Sergipe for the technical help in the composition of figures 01 and 02.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML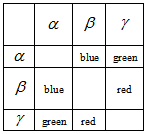




 and
and  for quarks
for quarks

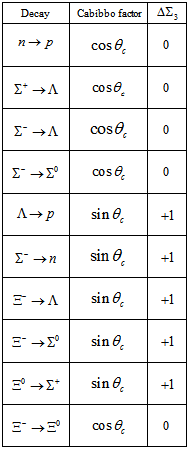
 with the CDF II Detector”, hep-ex arXiv:1301.0949v1, Jan 2013, to be published in Proceedings of Science.
with the CDF II Detector”, hep-ex arXiv:1301.0949v1, Jan 2013, to be published in Proceedings of Science.