-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2013; 3(2): 71-80
doi:10.5923/j.fs.20130302.04
A New Model without Dark Matter for the Rotation of Spiral Galaxies: the Connections among Shape, Kinematics and Evolution
Mario Everaldo de Souza
Departmento de Física, Universidade Federal de Sergipe, São Cristovão, 49100-000, Brazil
Correspondence to: Mario Everaldo de Souza , Departmento de Física, Universidade Federal de Sergipe, São Cristovão, 49100-000, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
It is proposed that the arms of spiral galaxies are formed by the continuous outflow of matter from their centers. It is then shown that the ratio between the radial and tangential velocities of the outflow is the parameter responsible for the logarithmic spiral structure of spiral galaxies. The fitting of some spiral galaxies to the model allows the calculation of the expansion velocities of matter in these galaxies and such values completely agree with the observational data. An approximate universal equation is proposed for the description of the arms of spiral galaxies with or without bars. Some important consequences are discussed with respect to dark matter, galactic evolution, cosmology, and the Milky Way. It is, particularly, concluded that dark matter does not exist in spiral galaxies.
Keywords: Spiral Galaxies, Spiral Structure of Galaxies, Dark Matter
Cite this paper: Mario Everaldo de Souza , A New Model without Dark Matter for the Rotation of Spiral Galaxies: the Connections among Shape, Kinematics and Evolution, Frontiers in Science, Vol. 3 No. 2, 2013, pp. 71-80. doi: 10.5923/j.fs.20130302.04.
Article Outline
1. Introduction
- The current status quo for the formation of the spiral structure in spiral galaxies is still based on the density wave theory which states that the matter of the disk becomes distributed in spiral arms due to the action of a wave-like perturbation in the form of quasi-steady global modes of the disk[1-3]. These three references are just examples of a long list of proposals within the same general framework. In this framework, of course, there would exist spiral galaxies of one type only, but as it is widely known spiral galaxies can be barred and non barred. Other approaches defend that the spiral structure is a short-lived, transient phenomenon triggered by gravitational instabilities. Two of many references in this line are[4] and[5]. A quite simple argumentation against the density wave theory is that according to this theory we would have to have many spirals with 3, 4, and even 5 arms. Observations, however, have shown that almost all spirals have only two arms. Also, according to this theory there would not exist asymmetric galaxies such as lopsided spirals. A very recent study by Foyle et al.[6] based on observations of 12 spiral galaxies discard the density wave theory in its simplest form as being an “important aspect of explaining spirals in large disk galaxies”, but the authors wrongly conclude that the spiral structure is not a long-livedphenomenon. This paper, actually, completely rules out the density wave theory. We present a new and alternative model for the description of spiral galaxies based on the outflow of matter from their cores and show that the spiral structure is inherent to the existence of the galaxy. Outflows of matter from the centers of galaxies have been reported since a long time ago. Let us present some examples. Very recent data[7] of NGC 6240, which is considered a typical protogalaxy show that “approximately 70\% of the total radio power at 20cm originates from the nuclear region (
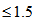 kpc), of which half is emitted by two unresolved (
kpc), of which half is emitted by two unresolved (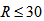 pc) cores and half by a diffuse component. Nearly all of the other 30% of the total radio power comes from an arm-like region extending westward from the nuclear region”. NGC 2992 presents a jet-like structure and a circum-nuclear ring[8]. Falcke and Biermann[9] report that there is a large scale emission-like jet going outward from the core of NGC 4258 with a mass of about
pc) cores and half by a diffuse component. Nearly all of the other 30% of the total radio power comes from an arm-like region extending westward from the nuclear region”. NGC 2992 presents a jet-like structure and a circum-nuclear ring[8]. Falcke and Biermann[9] report that there is a large scale emission-like jet going outward from the core of NGC 4258 with a mass of about 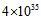 kg and with a kinetic power of approximately
kg and with a kinetic power of approximately 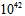 ergs/s and expansion velocity of about 2000km/s. Brunthaler et al.[10] report the first superluminal jet with a velocity of about 1.25c in the Seyfert spiral galaxy III Zw 2. For superluminal as well as subluminal speeds within physical media one must see[11]. Balmaverde and Capetti[12] have reported in 2006 that “Considering the radio structure, several objects of our CoreG sample have a radio-morphology with well developed jets and lobes: UGC 7360, UGC 7494 and UGC 7654 are FR I radio-galaxies part of the 3C sample (3C 270, 3C 272.1 and 3C 274), while in the Southern sample we have the well studied radio-galaxies NGC 1316 (Fornax A), a FR II source, NGC 5128 (Cen A) and IC 4296. A literature search shows that at least another 11 sources have extended radio-structures indicative of a collimated outflow, although in several cases this can only be seen in high resolution VLBI images, such as the mass scale double-lobes in UGC 7760 or the one-sided jet of UGC 7386”. Sturm et al.[13] have just reported massive molecular outflows from the centers of ultraluminous infrared galaxies (ULIRGs). As the authors state the terminal velocities in some of these outflows exceed 1000 km/s “and their outflow rates (up to ~ 1200 solar masses per year) are several times larger than their star formation rates”. Middleberg et al.[14] report radio observation of the Seyfert galaxies NGC 7674, NGC 5506, NGC 2110 and Mrk 1210, and conclude that “Our results confirm and extend earlier work showing that the outward motion of radio components in Seyfert galaxies is non-relativistic on pc scale. We briefly discuss whether this non-relativistic motion is intrinsic to the jet-formation process ….” Muñoz-Tuñon and Beckman[15] analyze the consequences of mass outflows in the circumnuclear zones of galaxies. They have found “in addition to a ring structure in the gas, there is often measurable expansion with higher radial velocities occurring near the nucleus” and also they show that “radially progressive bursts of star formation can account for a wide range of these observed phenomena and could be related to the presence of liners in the interstellar medium close to the nucleus.” On April 2011 Alatalo et al.[16] have reported the discovery of an AGN-Driven Molecular Outflow in the early-type galaxy NGC 1266 which is classified as an S0 without arms. The molecular outflow has a molecular mass of
ergs/s and expansion velocity of about 2000km/s. Brunthaler et al.[10] report the first superluminal jet with a velocity of about 1.25c in the Seyfert spiral galaxy III Zw 2. For superluminal as well as subluminal speeds within physical media one must see[11]. Balmaverde and Capetti[12] have reported in 2006 that “Considering the radio structure, several objects of our CoreG sample have a radio-morphology with well developed jets and lobes: UGC 7360, UGC 7494 and UGC 7654 are FR I radio-galaxies part of the 3C sample (3C 270, 3C 272.1 and 3C 274), while in the Southern sample we have the well studied radio-galaxies NGC 1316 (Fornax A), a FR II source, NGC 5128 (Cen A) and IC 4296. A literature search shows that at least another 11 sources have extended radio-structures indicative of a collimated outflow, although in several cases this can only be seen in high resolution VLBI images, such as the mass scale double-lobes in UGC 7760 or the one-sided jet of UGC 7386”. Sturm et al.[13] have just reported massive molecular outflows from the centers of ultraluminous infrared galaxies (ULIRGs). As the authors state the terminal velocities in some of these outflows exceed 1000 km/s “and their outflow rates (up to ~ 1200 solar masses per year) are several times larger than their star formation rates”. Middleberg et al.[14] report radio observation of the Seyfert galaxies NGC 7674, NGC 5506, NGC 2110 and Mrk 1210, and conclude that “Our results confirm and extend earlier work showing that the outward motion of radio components in Seyfert galaxies is non-relativistic on pc scale. We briefly discuss whether this non-relativistic motion is intrinsic to the jet-formation process ….” Muñoz-Tuñon and Beckman[15] analyze the consequences of mass outflows in the circumnuclear zones of galaxies. They have found “in addition to a ring structure in the gas, there is often measurable expansion with higher radial velocities occurring near the nucleus” and also they show that “radially progressive bursts of star formation can account for a wide range of these observed phenomena and could be related to the presence of liners in the interstellar medium close to the nucleus.” On April 2011 Alatalo et al.[16] have reported the discovery of an AGN-Driven Molecular Outflow in the early-type galaxy NGC 1266 which is classified as an S0 without arms. The molecular outflow has a molecular mass of 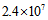 Msuns. As the authors observe “The star formation in NGC 1266 is insufficient to drive the outflow, and thus it is likely driven by the active galactic nucleus (AGN)”. A very important work that shows the initial formation of spiral arms in a galaxy is the paper of Stark et al.[17] entitled The formation and assembly of a typical star-forming galaxy at redshift
Msuns. As the authors observe “The star formation in NGC 1266 is insufficient to drive the outflow, and thus it is likely driven by the active galactic nucleus (AGN)”. A very important work that shows the initial formation of spiral arms in a galaxy is the paper of Stark et al.[17] entitled The formation and assembly of a typical star-forming galaxy at redshift 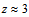 . The authors report studies of a galaxy about 2-3 Gyr after the Big Bang. One of the very significant results of the work is the regular, bi-symmetric velocity field revealed by the O III emission lines measurements. Examining the velocity field in more detail, the authors extracted a rotation curve with a circular velocity of about 67 km/s. Figure 1 of the article clearly shows an arm-like structure. Mark Swinbank who is one of the authors, commenting on the paper on the site EurekAlert![18], has said that “The distribution of gas seen with our amazing resolution indicates we are witnessing the gradual build-up of a spiral disk with a central nuclear component”. Recently, in 2001, Wilson et al.[19], using high resolution X-ray observations with Chandra, have managed to solve the puzzle concerning the anomalous ghostly opposite arms of M106 (NGC 4258) which are dominated by young stars: they are jets that originate in the nucleus of the galaxy. Another aspect of the subject is provided by analyses of metalicity gradients in spiral galaxies. The NED/IAC/Caltech document[20] on this issue is a thorough text which takes into account the works of many researchers. The text shows that the data for the Milky Way are in line with those from other spirals, and that the metalicity data expressed in terms of
. The authors report studies of a galaxy about 2-3 Gyr after the Big Bang. One of the very significant results of the work is the regular, bi-symmetric velocity field revealed by the O III emission lines measurements. Examining the velocity field in more detail, the authors extracted a rotation curve with a circular velocity of about 67 km/s. Figure 1 of the article clearly shows an arm-like structure. Mark Swinbank who is one of the authors, commenting on the paper on the site EurekAlert![18], has said that “The distribution of gas seen with our amazing resolution indicates we are witnessing the gradual build-up of a spiral disk with a central nuclear component”. Recently, in 2001, Wilson et al.[19], using high resolution X-ray observations with Chandra, have managed to solve the puzzle concerning the anomalous ghostly opposite arms of M106 (NGC 4258) which are dominated by young stars: they are jets that originate in the nucleus of the galaxy. Another aspect of the subject is provided by analyses of metalicity gradients in spiral galaxies. The NED/IAC/Caltech document[20] on this issue is a thorough text which takes into account the works of many researchers. The text shows that the data for the Milky Way are in line with those from other spirals, and that the metalicity data expressed in terms of 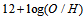 decreases with the distance from the centers of spirals, clearly showing that their disks are younger than their bulges and that the hydrogen has its origin in the centers of galaxies. Taking a closer look at the morphologies of some galaxies we can clearly see jets or arms coming out from their nuclei. It is the case of some galaxies classified as peculiar galaxies as those shown below in Figures 1, 2, 3, and 4 that have high redshifts. All pictures of UBVR images (UGC´s and VV 114*) shown in figures 1, 2, 3, and 4 are credited to Hibbard, Liu and Armus[21].
decreases with the distance from the centers of spirals, clearly showing that their disks are younger than their bulges and that the hydrogen has its origin in the centers of galaxies. Taking a closer look at the morphologies of some galaxies we can clearly see jets or arms coming out from their nuclei. It is the case of some galaxies classified as peculiar galaxies as those shown below in Figures 1, 2, 3, and 4 that have high redshifts. All pictures of UBVR images (UGC´s and VV 114*) shown in figures 1, 2, 3, and 4 are credited to Hibbard, Liu and Armus[21]. 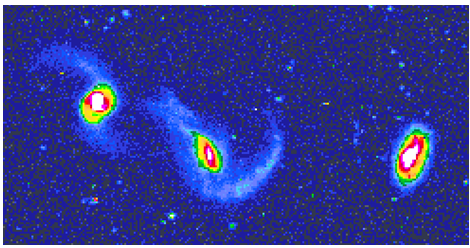 | Figure 2. UBVR image of UGC 06748*. On the left we see a pair of interacting spiral galaxies with young arms. Figure credited to Hibbard, Liu and Armus[21] |
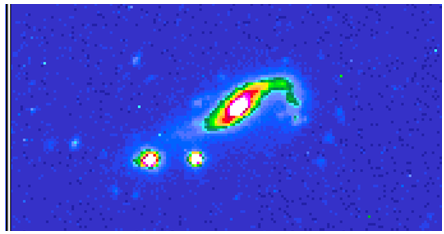 | Figure 3. UBVR image of a very young arm just beginning to curve in UGC 08929*. Observe the protuberance on the opposite side. UGC 06748*. Figure credited to Hibbard, Liu and Armus[21] |
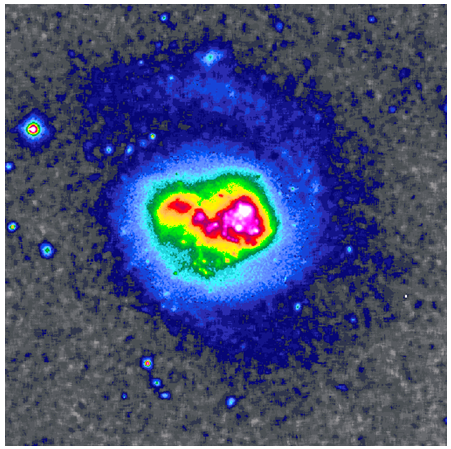 | Figure 4. Spiral arms just being formed in spiral galaxy VV 114* (Arp 236). Figure credited to Hibbard, Liu and Armus[21] |
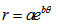 | (1) |
 and
and  are just constants which can be appropriately chosen.
are just constants which can be appropriately chosen.2. The Model
- Taking into account what was shown and discussed above this work proposes that the spiral arms are formed by the shedding of matter from the nuclei of spiral galaxies. This is actually an old idea, proposed in 1964 by Oki et al.[23]. So, let us consider that a certain extended mass of gas
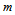 is ejected from the bulge of the galaxy with a radial velocity
is ejected from the bulge of the galaxy with a radial velocity 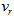 as is shown in Fig. 5. In the bulge the mass
as is shown in Fig. 5. In the bulge the mass 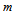 was rotating with an angular velocity
was rotating with an angular velocity 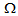 . When it leaves the bulge at a later time
. When it leaves the bulge at a later time 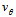 is not affected by the radial driving forces that cause the shedding of matter, and as it is shown below the mass keeps the tangential velocity approximately constant because of conservation of the angular momentum. Let us recall again that
is not affected by the radial driving forces that cause the shedding of matter, and as it is shown below the mass keeps the tangential velocity approximately constant because of conservation of the angular momentum. Let us recall again that 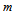 is not pointlike.
is not pointlike. 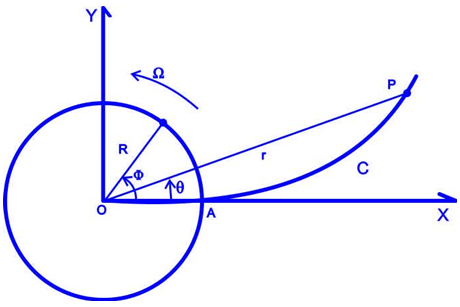 | Figure 5. While the bulge sweeps an angle  , the mass , the mass  makes an angle makes an angle 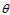 in its displacement from in its displacement from 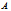 to to 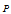 |
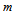 frequently has the form of an arc of matter which gets approximately distributed along a spiral so that we have an equation of the form for the angular momentum of
frequently has the form of an arc of matter which gets approximately distributed along a spiral so that we have an equation of the form for the angular momentum of 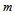
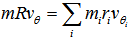 | (2) |
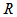 is the radius of the bulge,
is the radius of the bulge, 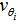 are the tangential velocities of the different parts of the extended mass
are the tangential velocities of the different parts of the extended mass 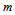 which are located at
which are located at 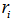 , just after having left the bulge. We notice that after having left the bulge the mass
, just after having left the bulge. We notice that after having left the bulge the mass 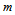 can continue with an average
can continue with an average 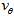 given by
given by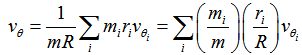 | (3) |
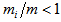 and
and 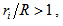
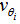 can thus have values around
can thus have values around 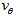 . We obtain more detail on this if we analyze the behavior of the kinetic energy. Just before leaving the bulge the mass
. We obtain more detail on this if we analyze the behavior of the kinetic energy. Just before leaving the bulge the mass 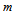 (in the form or an arc, for example) has the kinetic energy
(in the form or an arc, for example) has the kinetic energy 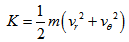 | (4) |
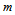 has the kinetic energy
has the kinetic energy 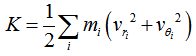 | (5) |
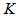 is constant across the border of the bulge, we obtain
is constant across the border of the bulge, we obtain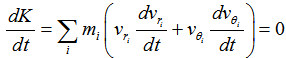 | (6) |
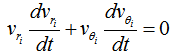 | (7) |
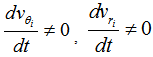 , and
, and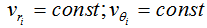 | (8) |
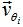 . The simple arguments above show that the constancy of the tangential velocity of spiral galaxies is directly related to the ejection of matter from their bulges and to the conservation of mass, energy and angular momentum. Thus
. The simple arguments above show that the constancy of the tangential velocity of spiral galaxies is directly related to the ejection of matter from their bulges and to the conservation of mass, energy and angular momentum. Thus 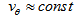 | (9) |
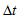 , the center of mass of the extended mass
, the center of mass of the extended mass 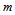 will be located at point P, at a distance
will be located at point P, at a distance 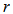 from the center O (Fig. 5), and since
from the center O (Fig. 5), and since 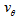 remains approximately constant, we have
remains approximately constant, we have 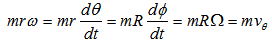 | (10) |
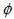 is the angle that the center of mass of
is the angle that the center of mass of 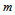 would have if it had not been ejected from the bulge, that is, it is the angle that the bulge made during the time interval
would have if it had not been ejected from the bulge, that is, it is the angle that the bulge made during the time interval 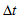 . Thus, Eq. (10) yields
. Thus, Eq. (10) yields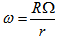 | (11) |
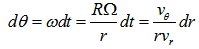 | (12) |
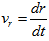 .At the bulge border the energy of the mass m (at point A in Fig 5) is equal to
.At the bulge border the energy of the mass m (at point A in Fig 5) is equal to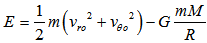 | (13) |
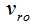 and
and 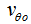 are the initial radial and tangential velocities of
are the initial radial and tangential velocities of  , and
, and  and
and 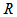 are the mass and radius of the bulge, respectively, and
are the mass and radius of the bulge, respectively, and 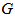 is Newton’s constant. At point P the energy is given by
is Newton’s constant. At point P the energy is given by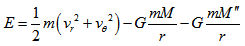 | (14) |
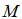 is the mass of the bulge and
is the mass of the bulge and 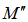 is the mass of the disk up to distance
is the mass of the disk up to distance 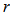 . Considering the disk as a flat cylinder of height
. Considering the disk as a flat cylinder of height 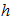 we can write
we can write 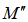 as
as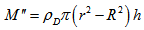 | (15) |
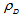 is the density of matter in the disk and
is the density of matter in the disk and 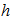 is the disk thickness. As the centers of galaxies and their bulges contain most of the mass, we can make
is the disk thickness. As the centers of galaxies and their bulges contain most of the mass, we can make 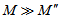 , and using conservation of energy we obtain
, and using conservation of energy we obtain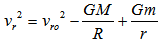 | (16) |
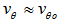 . But
. But 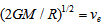 is the escape velocity from the bulge, and thus, we can write
is the escape velocity from the bulge, and thus, we can write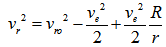 | (17) |
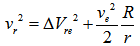 | (18) |
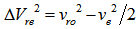 . The above equation can be written as
. The above equation can be written as 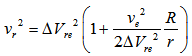 | (19) |
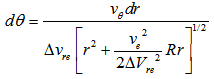 | (20) |
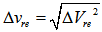 . Eq. (20) can still be given by
. Eq. (20) can still be given by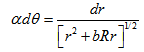 | (21) |
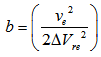 and
and 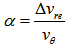 . Eq. (21), solved with the initial condition
. Eq. (21), solved with the initial condition 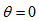 for
for 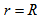 , yields
, yields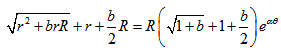 | (22) |
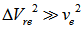 ,
, 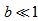 , and then we have
, and then we have 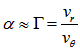 , and we obtain
, and we obtain 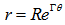 | (23) |
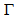 is a very important parameter, directly related to the kinematics of the galaxy. It was deduced by de Souza quite some time ago[24,25]. Danvar equation is only valid if the initial radial velocity is much larger than the escape velocity from the bulge. This is an important information on the AGN of spiral galaxies.
is a very important parameter, directly related to the kinematics of the galaxy. It was deduced by de Souza quite some time ago[24,25]. Danvar equation is only valid if the initial radial velocity is much larger than the escape velocity from the bulge. This is an important information on the AGN of spiral galaxies.2.1. The Differential Rotation of Spiral Galaxies
- Substituting Eq. (23) into Eq. (11) we obtain
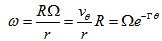 | (24) |
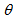 . Eq. (24) is the very known differential rotation that takes place in the disks of spiral galaxies. Since
. Eq. (24) is the very known differential rotation that takes place in the disks of spiral galaxies. Since 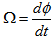 ,
, 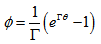 | (25) |
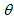 for a certain spiral arm we can find the maximum value of
for a certain spiral arm we can find the maximum value of 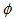 and find out how much the bulge rotated since the beginning of the formation of that particular spiral arm. Of course, this is very important for studying galactic evolution. We can also define the lagging angle
and find out how much the bulge rotated since the beginning of the formation of that particular spiral arm. Of course, this is very important for studying galactic evolution. We can also define the lagging angle 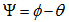 (Fig. 6).
(Fig. 6).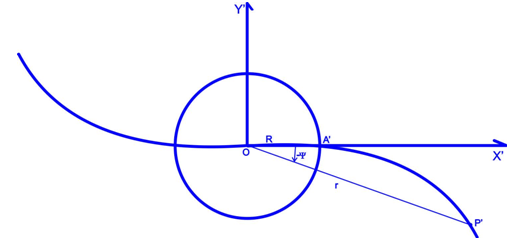 | Figure 6. The lagging angle 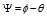 which is measured with respect to the initial stream of matter, across a dimater of the bulge by an observer corotating with the bulge. which is measured with respect to the initial stream of matter, across a dimater of the bulge by an observer corotating with the bulge. |
2.2. The Upper Mass Limit for a Spiral Galaxy
- The condition
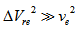 means that
means that 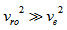 that yields the upper limit for the mass of a spiral galaxy, given by
that yields the upper limit for the mass of a spiral galaxy, given by 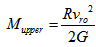 | (26) |
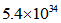 kg which is very consistent since its total mass is estimated as being about
kg which is very consistent since its total mass is estimated as being about 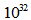 kg.
kg. 3. Application of the Model to Some Spiral Galaxies
- We considered that Danvar equation is valid and applied it to some spirals. The number of galaxies of the sample was limited by the information on the velocity of radial outflows in galaxies. In all galaxies below the data points were visually captured with the use of the software plot digitalizer following a dust lane or bright stars. The respective error bars were estimated and are indicated for each case.
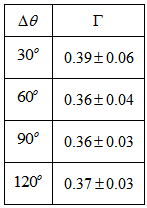
3.1. M51 (NGC 5194)
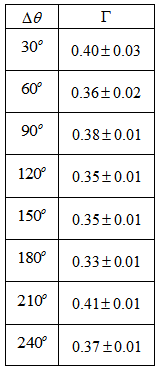
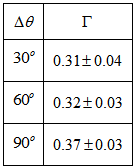
- We followed the black dust lane of the lower arm in Fig. 7 below (the arm that goes towards M51B). We took the lagging angle
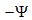 with respect to the beginning of the arm, that is, with respect to
with respect to the beginning of the arm, that is, with respect to 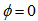 , and thus,
, and thus, 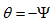 in intervals of , and measured the corresponding values of
in intervals of , and measured the corresponding values of 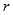 . The calculated values of
. The calculated values of 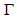 are shown on Table 1. The average value of
are shown on Table 1. The average value of 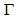 is
is 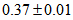 , and thus
, and thus 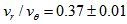 .On p. 1151 of their paper Shetty et al.[28] present a detailed analysis of
.On p. 1151 of their paper Shetty et al.[28] present a detailed analysis of 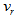 and
and 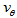 in terms of an arm phase angle defined by the authors. It is clearly shown that
in terms of an arm phase angle defined by the authors. It is clearly shown that 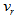 values vary around 50km/s and
values vary around 50km/s and 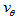 have values around 150km/s, and thus the ratio
have values around 150km/s, and thus the ratio 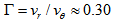 is quite close to the above value of
is quite close to the above value of 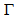 . As we will see below this is, actually, the worst discrepancy.
. As we will see below this is, actually, the worst discrepancy. | Figure 7. For M51 (NGC 5194) we considered data points along the dust lane as shown above |
|
3.2. M74 (NGC 628)
- In this case we considered points corresponding to bright stars around the middle of the arm. We took the lagging angle as in the case of M51.According to Fathi et al.[29] for NGC 628 (M74)
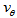 is about 170 km/s and according to Ganda et al.[30] its
is about 170 km/s and according to Ganda et al.[30] its 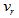 is about 65 km/s, and thus,
is about 65 km/s, and thus, 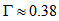 which is quite close to our calculated values above (Table 2) whose average is
which is quite close to our calculated values above (Table 2) whose average is 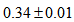 . Reference[30] data refer to the dispersion velocity (
. Reference[30] data refer to the dispersion velocity (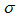 ) data of 18 spiral galaxies, but the radial outflow velocity is
) data of 18 spiral galaxies, but the radial outflow velocity is 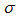 in the radial direction because
in the radial direction because 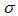 is the velocity of the gas after the subtraction of the circular velocity. Fathi et al.[29] have also measured the dependence of the angular velocity of NGC 628 (M74) with respect to the distance to the center of the galaxy. Their results agree approximately with Eq (11) because according to Fig. 7 of their paper
is the velocity of the gas after the subtraction of the circular velocity. Fathi et al.[29] have also measured the dependence of the angular velocity of NGC 628 (M74) with respect to the distance to the center of the galaxy. Their results agree approximately with Eq (11) because according to Fig. 7 of their paper 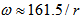 for
for 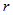 between 1.9 kpc and 11 kpc, with
between 1.9 kpc and 11 kpc, with 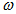 in km/(kpc)s and in kpc. For example,
in km/(kpc)s and in kpc. For example, 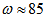 km/(kpc)s for
km/(kpc)s for 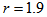 kpc, and
kpc, and 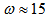 km/(kpc)s for
km/(kpc)s for 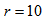 kpc.
kpc.
|
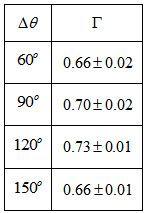
3.3. NGC 1300
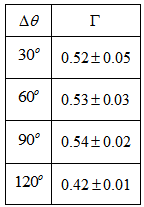
- As in the previous example, intervals of were used along the dust lane of the lower arm (Fig. 8). The calculated values are shown on Table 3.
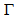 decreases too much above
decreases too much above 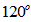 , probably because, due to its shape, the arm is attracted a lot towards the bar. The average of the calculated values below is
, probably because, due to its shape, the arm is attracted a lot towards the bar. The average of the calculated values below is 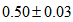 .According to Aguerri et al.[31]
.According to Aguerri et al.[31] 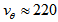 km/s and Lindblad et al. [32] report a
km/s and Lindblad et al. [32] report a 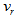 in the arms of the order of 120 km/s, yielding, thus, a value of
in the arms of the order of 120 km/s, yielding, thus, a value of 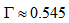 which is very close to the calculated values above.
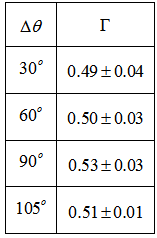
which is very close to the calculated values above. 3.4. NGC 4030
- In this case, since the bulge is very fuzzy, we considered angular differences with respect to a baseline across the center of the nucleus. Table 4 presents the results whose average value is
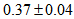 .Ganda et al.[30] report a value
.Ganda et al.[30] report a value 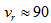 km/s and Mathewson \& Ford[33] say that
km/s and Mathewson \& Ford[33] say that 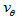 is about 236 km/s, and, thus,
is about 236 km/s, and, thus, 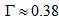 which is quite close to the above calculated average value.
which is quite close to the above calculated average value. | Figure 8. We considered the dust lane of the lower arm of NGC 1300 for the fitting (NASA/HST photo) |
|
|
3.5. NGC 1042
- We performed the fitting in the longer arm following very bright stars, in intervals of
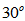 . The calculated values for
. The calculated values for 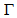 are listed on Table 5 and their average value is about
are listed on Table 5 and their average value is about 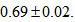 Ganda et al.[30] report
Ganda et al.[30] report 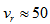 km/s and Kornreich et al.[34] present
km/s and Kornreich et al.[34] present 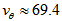 km/s which yield
km/s which yield 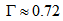 that is very close to our average value above. Therefore, this galaxy is more like a barred spiral.
that is very close to our average value above. Therefore, this galaxy is more like a barred spiral.
|
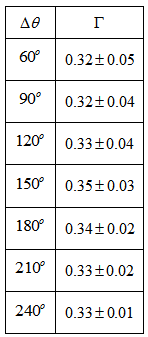
3.6. NGC 4254
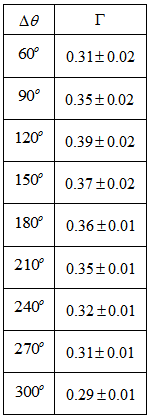
- Figure 9 shows how the three arms of this very asymmetric galaxy were labeled, and Tables 6, 7 and 8 present the calculated values of
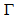 . We considered bright stars along the arms.
. We considered bright stars along the arms. | Figure 9. The three arms of NGC 4254 considered for the fitting (Photo by Teresa OKeefe and Jeff Lawrey/Adam Block/NOAO/AURA/NSF) |
 km/s and Kornreich et al.[34]
km/s and Kornreich et al.[34] 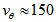 km/s that yield
km/s that yield 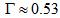 which is very close to the average value of
which is very close to the average value of 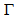 of Table 6 which is
of Table 6 which is 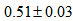 . And now we can understand why this galaxy is so asymmetric: arm A has a larger radial velocity than arms B and C, and has a
. And now we can understand why this galaxy is so asymmetric: arm A has a larger radial velocity than arms B and C, and has a 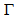 value of arms of barred spirals. With the above average values of
value of arms of barred spirals. With the above average values of 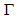 (
(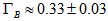 , and
, and 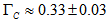 ) for arms B and C we find that their radial velocities are approximately equal to 49.5 km/s which is much smaller than the radial velocity of arm A.
) for arms B and C we find that their radial velocities are approximately equal to 49.5 km/s which is much smaller than the radial velocity of arm A.
|
|
|
4. Discussion of Results
- We clearly see that the results are consistent and the parameter
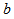 of the Danvar equation is the ratio
of the Danvar equation is the ratio 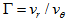 and it is, thus, directly connected to the kinematics of the galaxy. This means that the shape of a spiral galaxy is directly connected to its kinematics and evolution. The arms of young spiral galaxies are small and old spiral galaxies have long arms. Therefore, a spiral galaxy unfolds itself from the inside out throughout time up to the exhaustion of the mass of its nucleus. And it does not get tightly wound as a consequence of the unfolding and winding because of the radial velocity . Of course, the nucleus should diminish slowly with time since its mass is shed outward. The Milky Way is still shedding matter outwards and there is a lot of mass in its center yet, and so it will keep on going during quite a while, probably a couple of billion years. The calculation of the parameter
and it is, thus, directly connected to the kinematics of the galaxy. This means that the shape of a spiral galaxy is directly connected to its kinematics and evolution. The arms of young spiral galaxies are small and old spiral galaxies have long arms. Therefore, a spiral galaxy unfolds itself from the inside out throughout time up to the exhaustion of the mass of its nucleus. And it does not get tightly wound as a consequence of the unfolding and winding because of the radial velocity . Of course, the nucleus should diminish slowly with time since its mass is shed outward. The Milky Way is still shedding matter outwards and there is a lot of mass in its center yet, and so it will keep on going during quite a while, probably a couple of billion years. The calculation of the parameter 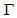 for a galaxy from the shape of its arms provides important information on its kinematics and will be very useful for the study of spiral galaxies. The above calculations and results mean that if
for a galaxy from the shape of its arms provides important information on its kinematics and will be very useful for the study of spiral galaxies. The above calculations and results mean that if 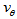 varied too much with
varied too much with 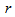 spiral galaxies would not exist at all. We immediately observe that most galaxies have not rotated much because of the following argumentation. Considering the ends of the arms of a spiral and taking the angular difference between them we obtain a certain
spiral galaxies would not exist at all. We immediately observe that most galaxies have not rotated much because of the following argumentation. Considering the ends of the arms of a spiral and taking the angular difference between them we obtain a certain 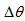 , and so we have the approximate relation
, and so we have the approximate relation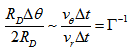 | (27) |
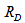 is the disk radius. Thus, we have
is the disk radius. Thus, we have 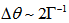 . For M51, for example,
. For M51, for example, 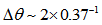 rad = 5.4 rad =
rad = 5.4 rad = 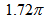 . Taking a look at its photo we observe that it has barely completed a full turn. The same holds for M74, for which
. Taking a look at its photo we observe that it has barely completed a full turn. The same holds for M74, for which 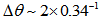 rad = 5.9 rad =
rad = 5.9 rad = 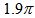 rad. We can see from its photo that it has just made a full turn. For NGC 1300 we obtain
rad. We can see from its photo that it has just made a full turn. For NGC 1300 we obtain 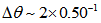 rad = 4 rad =
rad = 4 rad = 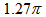 which is very consistent since it has just made a half turn. Therefore,
which is very consistent since it has just made a half turn. Therefore, 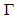 can be used to estimate the age of a spiral galaxy since the shedding of matter outward should begin in its first stages.According to what was developed above there should exist a redshift cut-off above which galaxies appear without arms. These are the extremely young galaxies that have not yet become spiral galaxies. Also, according to what was shown above young spiral galaxies should have small spiral arms and old galaxies should have well developed arms, that is, long arms. For the latter we can choose the nearby galaxies. In order to avoid any bias with respect to this we considered the Nobeyama CO Atlas of Nearby Spiral Galaxies[35] which is a survey of 40 nearby spiral galaxies with low redshifts. Taking out of the survey the flocculent and purely disk galaxies we clearly observe that all the other galaxies have well developed arms, and many of them have long spiral arms with at least a full turn. On the other hand the young spiral galaxies of the Hubble Deep Field (HDF)[36] and Hubble Ultra Deep Field (HUDF)[36] surveys present short or very short arms. Some of the results of the Hubble Deep Field survey are discussed by Dawson[37] in his PhD thesis. On page 84 of his thesis he says ``Careful, multi-wavelength morphological studies of the HDF-N reveal no galaxies with any kind of recognizable spiral structure at $z>2$ (Dickinson 2000). To wit, the redshift distribution of a sample of 52 late-type spiral and irregular galaxies complete to $K<20.47$ shows a dramatic cut-off at $z \sim 1.4$, with only two galaxies in the sample exceeding this limit (Rodighiero et al. 2000). Similarly, a combined photometric redshift / morphological data set complete to $I<26.0$ shows a sharp drop in the spiral galaxy distribution at $z>1.5$ (Driver et al. 1998). Specifically, in the $22<{I_{AB}}<23$ magnitude bin, there are no spiral galaxies beyond $z>1.5$; in the $23<{I_{AB}}<24$ magnitude bin, there is only one.''
can be used to estimate the age of a spiral galaxy since the shedding of matter outward should begin in its first stages.According to what was developed above there should exist a redshift cut-off above which galaxies appear without arms. These are the extremely young galaxies that have not yet become spiral galaxies. Also, according to what was shown above young spiral galaxies should have small spiral arms and old galaxies should have well developed arms, that is, long arms. For the latter we can choose the nearby galaxies. In order to avoid any bias with respect to this we considered the Nobeyama CO Atlas of Nearby Spiral Galaxies[35] which is a survey of 40 nearby spiral galaxies with low redshifts. Taking out of the survey the flocculent and purely disk galaxies we clearly observe that all the other galaxies have well developed arms, and many of them have long spiral arms with at least a full turn. On the other hand the young spiral galaxies of the Hubble Deep Field (HDF)[36] and Hubble Ultra Deep Field (HUDF)[36] surveys present short or very short arms. Some of the results of the Hubble Deep Field survey are discussed by Dawson[37] in his PhD thesis. On page 84 of his thesis he says ``Careful, multi-wavelength morphological studies of the HDF-N reveal no galaxies with any kind of recognizable spiral structure at $z>2$ (Dickinson 2000). To wit, the redshift distribution of a sample of 52 late-type spiral and irregular galaxies complete to $K<20.47$ shows a dramatic cut-off at $z \sim 1.4$, with only two galaxies in the sample exceeding this limit (Rodighiero et al. 2000). Similarly, a combined photometric redshift / morphological data set complete to $I<26.0$ shows a sharp drop in the spiral galaxy distribution at $z>1.5$ (Driver et al. 1998). Specifically, in the $22<{I_{AB}}<23$ magnitude bin, there are no spiral galaxies beyond $z>1.5$; in the $23<{I_{AB}}<24$ magnitude bin, there is only one.''4.1. Distinction between Barred and Non-barred Spiral Galaxies
- We observe that with respect to the tangential velocity, barred spirals have larger radial velocities (expansion velocities) than non–barred spirals and that is why their spiral arms are more open, that is, less tightly wound. Analyzing more galaxies we can establish what the minimum value of
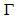 for a barred spiral.
for a barred spiral. 4.2. Studies on Asymmetry in Spiral Galaxies
- The measurement of $\Gamma $ by means of the spiral arms will enable us to study what is going on in asymmetric galaxies as we did above for the case of NGC 4254.
4.3. Consequences for the Milky Way
- The tangential velocity of the Milky Way is about 220 km/s[28] and at our galactic longitude
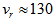 km/s[28], so that
km/s[28], so that 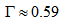 and, thus, the Milky Way is probably a barred spiral. And now, knowing its
and, thus, the Milky Way is probably a barred spiral. And now, knowing its 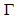 we can calculate the shape of its arms.
we can calculate the shape of its arms.4.4. Cosmological Consequences
- We should readdress the time of galaxy formation because, according to the above results, galaxies were formed much earlier than what is presently considered. And since spirals were small when they were young, they probably were formed from quasars which is an old idea proposed by de Souza[38],[40] and Arp[39]. This agrees very well with the findings of the HDF and HUDF surveys.
4.5. Consequences for Dark Matter
- We observe that the dynamics of the disk of a spiral galaxy is mainly dictated by
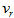 ,
, 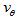 and its ratio
and its ratio 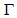 , and
, and 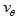 is approximately constant in the disk because the driving forces that shed matter outward are radial forces and do no work on the perpendicular direction, and thus, cannot change
is approximately constant in the disk because the driving forces that shed matter outward are radial forces and do no work on the perpendicular direction, and thus, cannot change 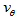 . Therefore, dark matter plays no role in the constancy of the tangential velocity of spiral galaxies. Actually, if dark matter existed,
. Therefore, dark matter plays no role in the constancy of the tangential velocity of spiral galaxies. Actually, if dark matter existed, 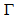 would not be approximately constant and, thus, spiral galaxies would not exist at all. Therefore, dark matter does not exist in spiral galaxies. It is worth noting that, very recently, dark matter has suffered two great blows: The papers by Moni-Bidin et al. [41] and Pawlowski et al.[42] have shown that dark matter does not exist at all in the Milky Way. On the other hand Geha et al.[43] have found that the dynamics of the dwarf galaxy NGC 147 can be explained without any need of dark matter. Since galaxies should be composed of the same type of matter we can just say that dark matter does not exist at all. Moreover, it is easy to see that dark matter has no place in Particle Physics due to the following argumentation. Particles are either fermions or bosons. As it is well known bosons do not clump together simply because they make the mediation between fermionic states. Thus, the supposed large volumes of dark matter cannot be composed of bosons. Therefore, dark matter would have to be composed of fermions, but from these we have to take out the baryons because baryons interact with light. Then, we are left with leptons, but only the light leptons (electron and neutrinos and their antiparticles) are stable. And also all leptons with mass are charged. This way dark matter would have to be composed of a very strange lepton that would have to have zero charge and be very massive, a WIMP. There is a very important question with respect to this proposal: where would the WIMP fit with respect to the 3 generations of fermions? Of course, it would not fit. It would have to be a particle of a separate generation of fermions. But the LHC did not find any new lepton. And Ahmed et al.[44] have presented the latest data on dark matter and have concluded that there is no WIMP with a mass below
would not be approximately constant and, thus, spiral galaxies would not exist at all. Therefore, dark matter does not exist in spiral galaxies. It is worth noting that, very recently, dark matter has suffered two great blows: The papers by Moni-Bidin et al. [41] and Pawlowski et al.[42] have shown that dark matter does not exist at all in the Milky Way. On the other hand Geha et al.[43] have found that the dynamics of the dwarf galaxy NGC 147 can be explained without any need of dark matter. Since galaxies should be composed of the same type of matter we can just say that dark matter does not exist at all. Moreover, it is easy to see that dark matter has no place in Particle Physics due to the following argumentation. Particles are either fermions or bosons. As it is well known bosons do not clump together simply because they make the mediation between fermionic states. Thus, the supposed large volumes of dark matter cannot be composed of bosons. Therefore, dark matter would have to be composed of fermions, but from these we have to take out the baryons because baryons interact with light. Then, we are left with leptons, but only the light leptons (electron and neutrinos and their antiparticles) are stable. And also all leptons with mass are charged. This way dark matter would have to be composed of a very strange lepton that would have to have zero charge and be very massive, a WIMP. There is a very important question with respect to this proposal: where would the WIMP fit with respect to the 3 generations of fermions? Of course, it would not fit. It would have to be a particle of a separate generation of fermions. But the LHC did not find any new lepton. And Ahmed et al.[44] have presented the latest data on dark matter and have concluded that there is no WIMP with a mass below 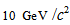 . Therefore, it is more than clear that dark matter does not exist at all.
. Therefore, it is more than clear that dark matter does not exist at all.4.6. The AGN Engine
- The values of
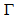 ,
, 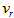 and
and 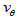 above presented for barred and unbarred spirals can be of some help in the search for the nature of the AGN engine that powers spiral galaxies.
above presented for barred and unbarred spirals can be of some help in the search for the nature of the AGN engine that powers spiral galaxies. 4.7. Bifurcation of Spiral Arms
- In the light of what was developed above we can understand how a spiral arm can bifurcate into two arms: it happens when the radial velocity changes to a lower or upper value. This is a phenomenon that takes place a lot in spirals. This is another contribution for the understanding of AGN's.
4.8. Irregular Galaxies
- Irregular galaxies are formed when the shedding of matter outward is done in a more chaotic way. In this case there may not exist any bipolar flow either. This means that in this case the outward flow has characteristics of an explosion.
5. Discussion of Results
- We have presented a new model for the formation of the arms of spiral galaxies which is directly connected to their kinematics and evolution in which the Danvar equation is derived from Newtonian Mechanics. The application of the model to some spiral galaxies shows full consistency with the available experimental data. We did not fit more galaxies because of a lack of data on the outflow velocities in spiral galaxies. We have then discussed some important consequences of the results. The results reached in this paper show that dark matter does not exist at all in spiral galaxies.
ACKNOWLEDGEMENTS
- I would like to thank Antonio de Freitas Lima, Lucílio Freitas and Jomara Costa for the technical support. I am deeply thankful to the Santilli Foundation, Prof. Ruggero Santilli, Dr. Richard Anderson, Prof. Christian Corda and Mrs. Carla Santilli for making possible the presentation of this work on September 9, 2011, in a plenary session of the San Marino Workshop on Cosmology and Astrophysics for Matter and Antimatter that happened from 5 to 9 September, 2011, in San Marino. I also thank the comment of an anonymous referee.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML