-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2013; 3(2): 49-55
doi:10.5923/j.fs.20130302.01
A Study on Separabilitybased on Realignment Criteria
Amit Bhar
Jogesh Chandra Chaudhuri College, Kolkata-700033, West Bengal, India
Correspondence to: Amit Bhar, Jogesh Chandra Chaudhuri College, Kolkata-700033, West Bengal, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A beautiful quantum event is the existence of inseparability in many body systems. Quantum system containing of two subsystems is separable if its density matrix can be expressed as 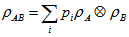 where
where 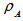 and
and 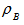 are density matrices for two subsystems where
are density matrices for two subsystems where 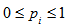 and
and 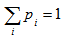 . Now people are involving in deep study last years various types of detection criterion and make implementation to the various states for detecting whether they are separable or not. In this work we just try to make a comparison of some separability criterion in a particular state and obtained a little bit consequences.
. Now people are involving in deep study last years various types of detection criterion and make implementation to the various states for detecting whether they are separable or not. In this work we just try to make a comparison of some separability criterion in a particular state and obtained a little bit consequences.
Keywords: Separability, Entanglement , Incomparability,Warner State, PPT, Cross norm
Cite this paper: Amit Bhar, A Study on Separabilitybased on Realignment Criteria, Frontiers in Science, Vol. 3 No. 2, 2013, pp. 49-55. doi: 10.5923/j.fs.20130302.01.
Article Outline
1. Introduction
- In the fundamental level nature requires quantum description rather than classical one. Now a days our interest spontaneously go to the entanglement in many bodyquantum systems. It is known to everybody that entanglement is a characteristic feature and powerful resource of quantum mechanics and is the basic ingredient of the foundation of the theory. To find the states which are useful for quantum information tasks, characterization of entangled states is of our great interest, this is called separability problem. This is one of the unsolved problems of quantum mechanics. Quantum inseparability first recognized by Einstein, Podolsky and Rosen[1] and Schrödinger[2,14] is one of the most astonishing features of quantum formalism. Recently people give their deep concentration to find out separability criteria in some particular states basically pure states and dynamical development of experimental methods and non-locality of quantum mechanics together inspire people to find out on the inseparability problems in quantum mechanics. Now there available several criterions to detect quantum entanglement of composite quantum states. But in the mixed states there no rigorous criteria for finding whether a state is entangled or not. Here we want to confined ourselves in positive partial transpose (PPT) criteria[4], computable cross norm or realignment criteria[5] and an other computable separability criteria[5]. According to Peres and Horodechi[3],PPT is a strong sufficient condition for detecting entanglement for 2×2 and 2×3 systems. On the way of searching some powerful criterion which will perform better than PPT criterion, some desirable results for detecting entanglement [6,7]. In this paper, we have performed a comparative study of these three criterions for a most general state of a composite quantum bipartite system.
2. Definitions and Explanations
- Bipartite Pure States:Let A and B be two non-interacting systems and
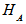 and
and 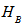 be their respective Hilbert spaces. The Hilbert space of the composite system is the tensor product
be their respective Hilbert spaces. The Hilbert space of the composite system is the tensor product 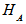 and
and 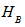 . If the system A is in the state
. If the system A is in the state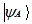 and system B is in the state
and system B is in the state 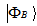 , then the composite system is in the state
, then the composite system is in the state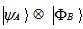 . The state of a composite system white can be represented in this form are called seperable states or product states. If there are states which can not be represented in this form are called entangled states. Let a projector
. The state of a composite system white can be represented in this form are called seperable states or product states. If there are states which can not be represented in this form are called entangled states. Let a projector 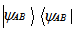 on a vector
on a vector 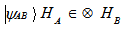 is a pure state if the local subsystems are pure states. For a pure state
is a pure state if the local subsystems are pure states. For a pure state 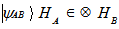 can be represented as
can be represented as 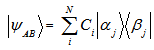 Where
Where 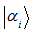 and
and 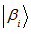 are the basis for
are the basis for 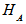 and
and 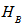 respectively,
respectively, 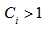 and
and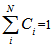 where
where 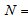 min(dim
min(dim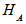 , dim
, dim 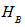 ). This decomposition of
). This decomposition of 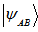 is called Schmidt decomposition and
is called Schmidt decomposition and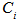 ’s are called Schmidt coefficients.Bipartite Mixed states[8-10,18,19]:Let
’s are called Schmidt coefficients.Bipartite Mixed states[8-10,18,19]:Let 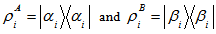 be respectively the states of the systems
be respectively the states of the systems 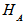 and
and 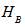 . Then combined state of their joint system can be written as
. Then combined state of their joint system can be written as 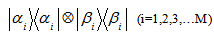 A necessary and sufficient condition of the mixed state
A necessary and sufficient condition of the mixed state 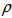 AB to be separable is that it can be represented as a convex combination of the product of projectors on local states as
AB to be separable is that it can be represented as a convex combination of the product of projectors on local states as 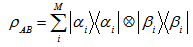 Otherwise, the mixed state is said to be entangled state.
Otherwise, the mixed state is said to be entangled state.3. Partial Transposition Criterion[11,12]
- A bipartite density matrix
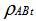 can be expressed as
can be expressed as 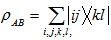 Where
Where 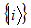 and
and 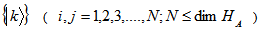 and
and 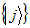 and
and 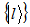
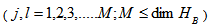 are orthogonal bases of
are orthogonal bases of 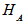 and
and 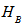 respectively.The partial transposition
respectively.The partial transposition 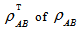 with respect to system A, is defined as
with respect to system A, is defined as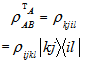 If
If 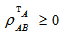 , that is the eigen values of
, that is the eigen values of 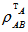 are non-negative then the state has positive partial transpose(PPT). Otherwise the state has non-positive partial transposition(NPT).Detection of entanglement:If any one of the eigen values of partial transposition of
are non-negative then the state has positive partial transpose(PPT). Otherwise the state has non-positive partial transposition(NPT).Detection of entanglement:If any one of the eigen values of partial transposition of 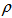 AB be negative then the state is entangled.
AB be negative then the state is entangled.4. Crossnorm or Realignment Criteria
- For a bipartite density matrix
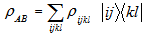 The realignment operation R
The realignment operation R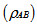 can be defined as[15-17]
can be defined as[15-17] 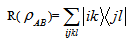 Detection of entanglement:If the sum of all the eigen values of R
Detection of entanglement:If the sum of all the eigen values of R 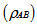 be less than or equal to 1 then the state is separable otherwise it is entangled.
be less than or equal to 1 then the state is separable otherwise it is entangled.5. A Computable Separability Criterion
- We consider Hilbert spaces
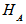 and
and 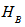 of the systems A and B respectively. Then there is a correspondence between states
of the systems A and B respectively. Then there is a correspondence between states 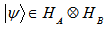 and Hilbert-Schmidt operators
and Hilbert-Schmidt operators 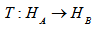 According to the rule :if
According to the rule :if 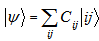 be decomposition of
be decomposition of 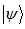 in terms of orthogonal bases
in terms of orthogonal bases 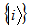 and
and 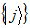 of
of 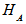 and
and 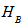 respectively. Then T
respectively. Then T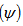 is given by
is given by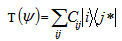 Conversely, if
Conversely, if 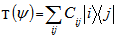 for some orthogonal bases
for some orthogonal bases 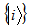 and
and 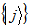 of
of  and
and 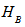 respectively,then
respectively,then 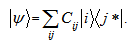 Theorem: If
Theorem: If 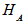 and
and 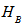 be finite dimentional Hilbert spaces and KA =HS(
be finite dimentional Hilbert spaces and KA =HS(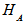 )
)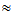 Cn and KB=HS(
Cn and KB=HS(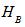 )
)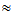 Cm be the spaces of Hilbert-Schmidt operators on
Cm be the spaces of Hilbert-Schmidt operators on 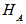 and
and 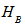 respectively.Then there exists a one to one correspondence between Hilbert-Schmidt operators T
respectively.Then there exists a one to one correspondence between Hilbert-Schmidt operators T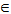 HS(
HS(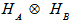 ) and Hilbert-Schimdt operators
) and Hilbert-Schimdt operators 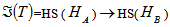 Detection of entanglement:We know that, for a finite dimentional Hilbert space
Detection of entanglement:We know that, for a finite dimentional Hilbert space 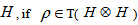 be a density operator then
be a density operator then 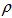 is separable imples the sum of squares of the eigen values
is separable imples the sum of squares of the eigen values 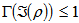 .
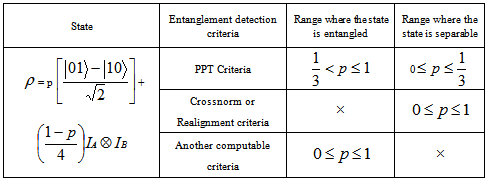
.6. Results in Details
- We consider a most general state
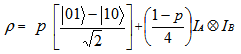 For this state, we are going to test where it is entangled and where separable using different types of entanglement detection criteria.At first for partial transpose criterion, the state is
For this state, we are going to test where it is entangled and where separable using different types of entanglement detection criteria.At first for partial transpose criterion, the state is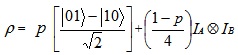 Taking partial transpose on the party B, we have
Taking partial transpose on the party B, we have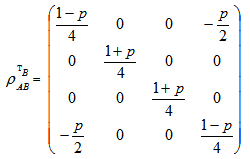 Eigen values of this matrix are given by
Eigen values of this matrix are given by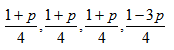 For the state to be separable , we have
For the state to be separable , we have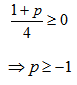 And
And 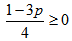
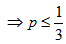 Since
Since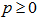 , the physical range of separability of
, the physical range of separability of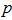 is
is 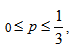 That is when
That is when 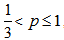 , the state is entangled.Now, we test for cross norm or realignment criterion, the realignment operator R
, the state is entangled.Now, we test for cross norm or realignment criterion, the realignment operator R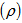 of the state
of the state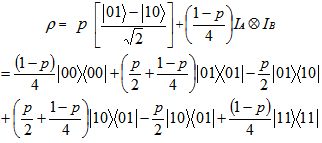 is given by
is given by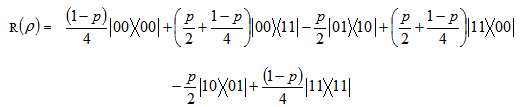 Now theeigen values are obtained as
Now theeigen values are obtained as 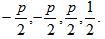 Sum of all the eigen values is
Sum of all the eigen values is 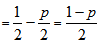 The is separable when
The is separable when 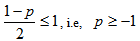 , but the physical range of p is
, but the physical range of p is 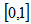 which implies that the state is separable for any value of p.Now for another computable separability criterion, we consider the same state
which implies that the state is separable for any value of p.Now for another computable separability criterion, we consider the same state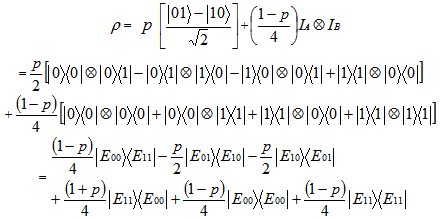 We write this state in matrix form as
We write this state in matrix form as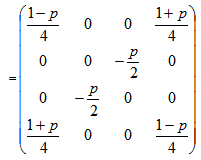 Therefore, we have
Therefore, we have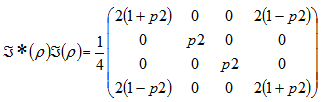 The eigen values of the above matrix are p 2,p2,4,p2Now, adding the absolute values of the square root of all eigen values, we arrive at
The eigen values of the above matrix are p 2,p2,4,p2Now, adding the absolute values of the square root of all eigen values, we arrive at 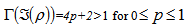 Hence we see that for all physical values of p, the state is entangled.In short, we represent the above results in tabular form asLet us consider a state
Hence we see that for all physical values of p, the state is entangled.In short, we represent the above results in tabular form asLet us consider a state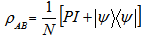 where
where 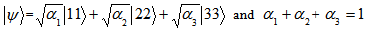
|
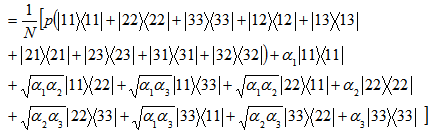 For normality, we have
For normality, we have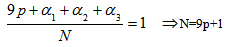
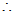 the state becomes,
the state becomes,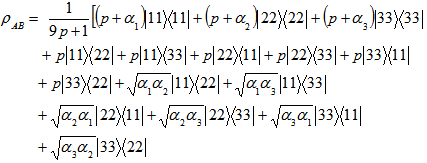 The realignment operator R
The realignment operator R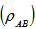 can be written as
can be written as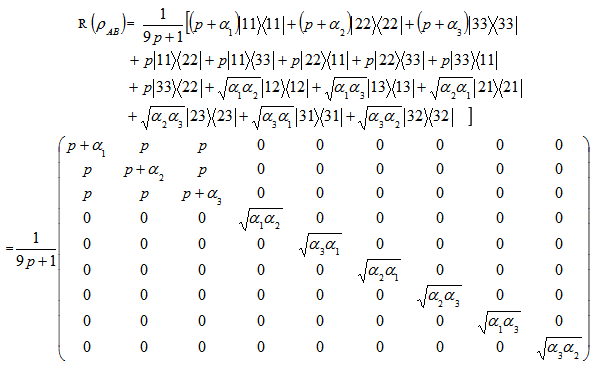 Sum of all the eigen values of the above matrix is
Sum of all the eigen values of the above matrix is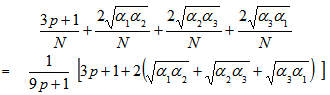 To find Min
To find Min 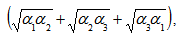 ,where
,where 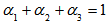 and we assume that
and we assume that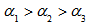 Then Min
Then Min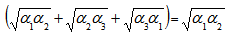 and Max
and Max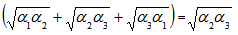 The state must be separable if
The state must be separable if 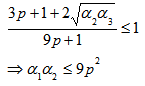 The state must be entangled if
The state must be entangled if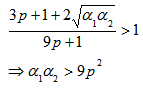 Partial Traspose Criteria:
Partial Traspose Criteria: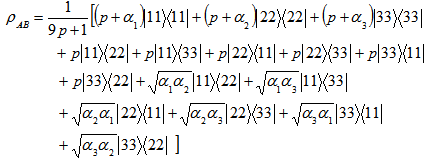 Taking Partial transpose on the party B, we get
Taking Partial transpose on the party B, we get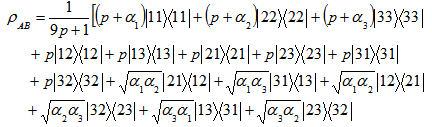 Now the eigen values of the above matrix are
Now the eigen values of the above matrix are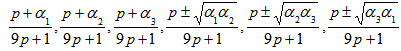 All of this eigen values are non-negative if
All of this eigen values are non-negative if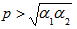 Therefore the state must be separable if
Therefore the state must be separable if 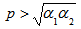 Which includes the separablelity condition for realignment criteria that is
Which includes the separablelity condition for realignment criteria that is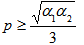 and
and 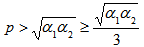 .
.7. Conclutions
- Now we come to the conclusion about the detection of entanglement of a general state using three strong entanglement detection criteria, we see that through the state is entangled when formed, PPT criteria shows that when p lies on[0,
 ], the state is separable and entangled on (
], the state is separable and entangled on (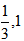 ]. But realignment criteria shows that the state is always separable whatever be the value of p. And the other criteria shows that the state is always entangled for any value of p. These conflicting results do not help us to reach to any concrete decision which one is stronger without any hesitations. So we can decide that PPT criteria is always strong criteria than others in
]. But realignment criteria shows that the state is always separable whatever be the value of p. And the other criteria shows that the state is always entangled for any value of p. These conflicting results do not help us to reach to any concrete decision which one is stronger without any hesitations. So we can decide that PPT criteria is always strong criteria than others in 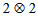 and
and 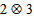 systems. Here PPT criteria exhibit more explicit and clear range of separability with respect to the other two methods. So in this paper through a detailed numerical search of the well known Warner state, it is clearly established that PPT is the reliable excellent criteria in the
systems. Here PPT criteria exhibit more explicit and clear range of separability with respect to the other two methods. So in this paper through a detailed numerical search of the well known Warner state, it is clearly established that PPT is the reliable excellent criteria in the 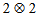 and
and 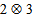 systems.
systems.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML