1. Introduction

Crimp in a textile strand is defined as the undulations or succession of waves or curls in the strand, induced either naturally during fiber growth, mechanically, or chemically. Crimp in a fiber is thus considered as the degree of deviation from linearity of a non straight fiber. Fiber crimp is the waviness of a fiber expressed as waves or crimps per unit length (figure 1) or as the difference between the lengths of the straightened and crimped fiber (expressed as a percentage of the straightened length)[1-3].

Fiber crimp characteristics have a big influence on the processing performance of the fibers. Crimp also contributes essentially to the properties of intermediate fiber assemblies, yarn and finished fabrics. Fiber crimp imparted to synthetic fibers, which are initially straight, makes it possible to process these fibers with existing machinery designed for natural fibers. Straight, slick synthetic fibers would not have sufficient cohesion for carding, combing, drawing, roving, and spinning. In nonwoven processes, crimp and crimp retention during processing are major contributors to processing efficiency, cohesion, fabric bulk and bulk stability.

1.1. Wave Length, Crimp Frequency and Crimp Length

The wave length λ of fiber crimp is twice the distance between two crossings of the fiber with the zero axis. It cannot be measured directly, since fiber crimp is by far too irregular and the small measuring quantities- wavelengths in the order of 1-3 mm - cause problems. Therefore, the crimp length lc, as the average length of fiber in one crimp, is sometimes used to describe crimp which can be measured as equation (1);

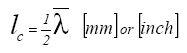(1)

More commonly used is the crimp frequency C_f may be calculated from the equation (2) of a fiber, defined as twice the average of the inverse of the wavelength. It is also called crimp number or crimp count, and characterizes the number of crimp bows or waves C_n per unit length of straightened fiber L₀. The unit length L₀ is taken as 1 inch in the US, whereas in Europe, 100 mm or 1 cm is used[2-6].

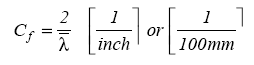(2)

1.2. Crimp Angle

The angle α between the leg of a crimp wave and the zero line may be used to characterize crimp geometry. The crimp angle φ is the angle between the two legs of a crimp bow, as shown in Figure 2; Φ indicates the sharpness of a crimp[2].

1.3. Crimp Amplitude and Crimp Index

The crimp amplitude A is the maximum distance of a crimp bow from the zero axes. Since the measurement of the amplitude of single crimp bows is practically impossible, average crimp amplitude of the fiber is derived geometrically with Pythagoras from length measurements of the crimped and the uncrimped fiber. The crimp index C_i is an indirect measure of the crimp amplitude. It is also called crimp ratio, crimp percentage, crimp contraction or crimp retraction and is the ratio of the difference of extended length L₀ and crimped length Lc of a fiber, in percent of the extended length of the fiber L₀ as shown in by the equation (3). C_i describes the crimp potential of a textile fiber as its ability to contract under tension.

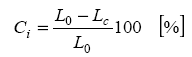(3)

A crimp index of zero (C_i = 0) indicates that the fiber is straight with no crimp. A crimp index of one (C_i = 1) indicates that in the relaxed state, the fiber is in collapsed loop form in the case of helical crimp, or ideally plied together at zero length in the case of planar crimp[3-4]. For a given crimp frequency C_f, the crimp index C_i is a measure for the crimp amplitude. Sometimes, the crimp index is denoted as percentage of the crimped length as the equation (4).

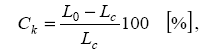
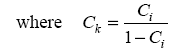(4)

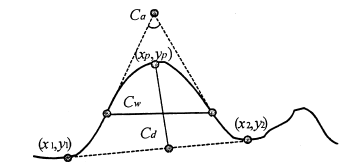
1.4. Crimp Width and Crimp Depth[^1]

These parameters were defined for the use in numerical image analysis of crimped fibers. The crimp width C_w is the distance between the midpoints of successive valleys of a crimp[4], as shown in Figure 3. The crimp depth C_d is the perpendicular distance between a peak of a crimp and a line joining the valleys of the adjacent crimp waves. C_w, C_d or C_w/C_d characterize the size of individual crimps (Figure 3). The mid points are determined by numerical regression of fitting curves. For an idealized triangular crimp bow, C_w corresponds to λ/2 and C_d corresponds to 2A[5,7].

1.5. Crimp Degree

The crimp degree Kg is defined as L0 / Lc, where L0 is the length of the straightened fiber and Lc is the length of the crimped fiber[9,12] .It is related to the crimp index by the equation (5);

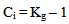(5)

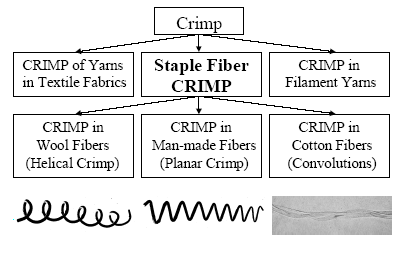Figure 1. Different types of crimp on textile substrates[1]

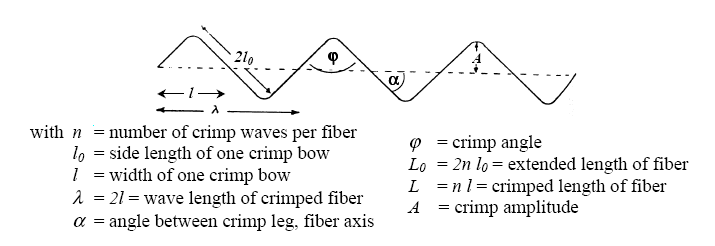Figure 2. Idealized geometry of the crimped fiber[2]

Figure 3. Irregular crimp wave with crimp descriptors[4]

1.6. Three-Dimensional Character of Crimp

Crimp form of textile fibers is essentially three-dimensional in character because the two parameters, geometric curvature and torsion, accurately describe the space path of fiber crimp. Measurements needed for determination of these parameters are tedious and impractical to obtain by manual methods. An instrument built by DuPont makes these measurements automatically [11,14]. It differs from published instrumental techniques by providing data which allow definition of torsion and curvature of crimp as well as the more usual the fiber crimp frequency and extensibility parameters[8, 12-13]. A measurement of a series of fibers shows that fiber crimp, expected to be planar by virtue of mechanical crimping process, and has a three-dimensional character. A curved line in space can be defined by curvature and torsion at any point along the line. These two quantities as a function of arc length of are basis for development of crimp parameters. Statistics of curvature and torsion distribution along a fiber and among fibers are also important descriptive parameters of crimp. Geometric torsion should not be confused with mechanical or fiber torsion, commonly called twist. Curvature is by definition a mathematical expression, which is more easily visualized in a physical sense than is geometric torsion. The mathematical statement of these parameters can be shown as by the equation (6).

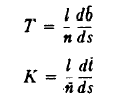(6)

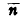The following diagram (figure 4) shows a curve in three-dimensional space (x, y, z Cartesian co-ordinates) for a crimp forming geometry over a textile surface. We generally used the torsion (T) and curvature (K) at any point on this curve can be defined in terms of three orthogonal vectors. The normal vectorwhich is in the direction of the radius of curvature, the tangent vector 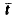which is tangent to the curve at the point and orthogonal to the normal vectors and the binomial vectors 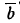which is orthogonal to the other two has been shown by this diagram. Curvature, K and torsion, T can be expressed in the x, y, z-co-ordinates system, so that data obtained by the automatic crimp-measuring instrument are used to calculate these parameters for any crimped fiber[13-15].

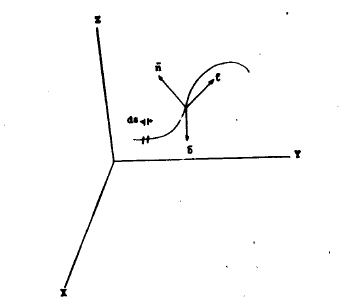Figure 4. Curve in three-dimensional space(x, y, z Cartesian co-ordinates) [15]

2. Crimp Distribution

The purpose of the study of fiber crimp distribution in nonwoven fabric is to quantify fiber mechanical behavior during de crimping and re-crimping, and relate it to fundamental fiber properties, nonwoven fabric properties, and process ability in nonwoven equipment by the study of crimp stability of fiber crimp in nonwoven fabrics. PET fibers of three different crimp levels have been carded and webs have been produced under various processing settings. Samples from different settings and processing stages are being tested for their single fiber crimp characteristics. An empirical function fitting the stress-strain curves of several single fibers in the crimp region has been found and may deliver parameters that characterize the crimp removal behavior of these fibers and their processing parameters. Synthetic fibers must be crimped to process on conventional carding equipment[16]. The initial crimp level and crimp retention during processing influence nonwoven fabric performance.

2.1. Effect of Crimp on Filtration Performance

Use of crimped rather than uncrimped fibers improves both efficiency and drag characteristics. The reason for the reduced drag and higher efficiency with crimped fibers may be found that straight fibers seem to form groups of two or more where the fibers run close together for a considerable length[17]. The space between them becomes clogged with filtered particles, and the group then acts as a single, wide, flat fiber with a higher resistance to air flow. Efficiency decreases because of the larger spaces between these groups. None of these groups is visible in the case of crimped fibers, which maintain an open structure.

2.2. Crimp Frequency

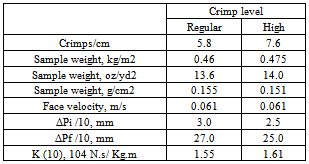
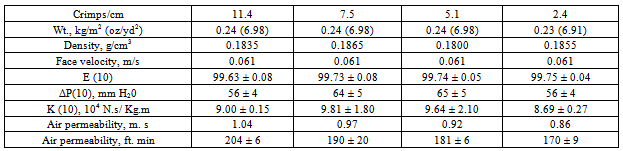
Experiments with fabrics made of crimped and uncrimped fibers showed that the crimped fabrics gave higher efficient lower pressure drop. This information is of limited value, since in practice uncrimped fibers are difficult to process and are therefore rarely used[15,18]. The extended study of the effects of crimp was therefore aimed at detecting any dependence on crimp level. It is done with two sets of fabrics. The first was made from three rayon fibers samples having crimp levels designated zero, normal (5.8 crimps/cm) and high (7.6crimps/cm). Micrographs of the three kinds of fiber are shown in Figure 5;

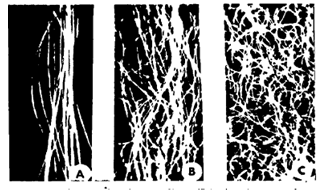Figure 5. Micrographs of rayon fibers (7.8X); A = no crimp, B = normal (5.8 crimps/cm), C = high crimp (7.6 crimps cm)[15]

Efficiencies of the three fabrics (weighing 0.17 kg ml) were measured using atmospheric dust and no cake, and the results are shown in Figure. In agreement with earlier results for a variety of fabrics when no dust cake forms, no differences in capture efficiencies are, seen. When the fabrics were used to filter a fly ash aerosol with accumulation of a dust cake, however, the results in figure were obtained. These show that in the presence of a cake, crimped fibers give slightly higher efficiencies than straight fibers. There is no significant advantage of high over normal crimp level, however. The advantage of crimped fibers over uncrimped extends into the diffusion region, showing again that the differences are probably due to different cake formations[12,19], since in the absence of a cake no differences in penetration were detected in this region.

Table 1. Pressure-drop characteristics on crimp level[19-20] Crimps, cm Density, g/cm3 K (1),104 N.s/ Kg.m K (10),104 N.s/ Kg.m Air permeability,m. s (ft. min) 7.6 0.112 0.99 2.17 1.52 (300) 5.8 0.112 1.05 2.67 1.43 (282) 0 0.112 1.29 3.35 1.28 (242)

With regard to pressure-drop characteristics, however, additional differences can be discerned. Table 1 gives results for two sets of experiments comparing the three rayon fabrics, and it can be seen that a higher crimp level brings higher air permeability and low specific cake resistance. The effect of crimp level on pressure-drop characteristics was also measured and the table 2 shows that at the tenth cycle the final pressure drops and specific cake resistance of both high and regular crimp samples are about equal[24-26].

Table 2. Pressure-drop characteristics on crimp level[24]

Table 3. Pressure-drop characteristics on crimp level[24,27]

Table 4. Structural characteristics of image series I[32]

The second set of fabrics mentioned above was made from specialty-crimped PET fiber. Because of the difficulty in securing a series of fibers with different levels of crimp, but differing only in that respect, crimper was constructed, and samples of fiber with four different levels of crimp were prepared from the same feeder yarn. The crimper operated by passing the yarn between a pair of heated gears, where a wavy configuration was imparted to it, matching the gear teeth in size and frequency[27]. Four pairs of inter-changeable gears were available, giving crimp frequencies of 236, 512, 748 and 1142 per meter (6, 13, 19, and 29 per inch). The crimped yarn was cut into 38-mm (1.5-in.) lengths and formed into nonwoven fabrics bonded with 10% rayon fiber. Attempts to make a’ fabric from uncrimped fiber failed because of the lack of coherence in the formed web. The performance-of these fabrics in filtering a fly ash aerosol is described in Table 3. Results indicate no discernible trend in performance with different crimp frequencies, either in capture efficiency or in cake resistance[24]. The Frazier air permeability, however, increases .with crimp frequency and this finding is common to the results shown in Table 3. This finding is not readily explained. Intuitively, it might be expected that with increasing crimp frequency, the spread in inter fiber spacing would be effectively reduced, so that wide spacing (i.e. large pores) would be fewer. This would result in lower permeability, but the observed trend is in the opposite direction, and the hypothesis must be rejected. Another possible explanation may be found in the observation that the rigidity of the felt decreases with increasing crimp frequency. This is not surprising, since single filament curvature increases with increasing crimp frequency, and thus the length of filament between bonding sites in the felt will likewise increase[28]. It follows (by analogy with rubber elasticity) that the modulus of a felt will be lower for the higher crimp frequencies. It is possible that, as a consequence, the higher-frequency felts stretched slightly during the permeability measurements, reducing resistance to air flow. In such a case the observed dependence of permeability on crimp frequency may be regarded as spurious.

2.3. Fiber orientation

The experiment were simulation and tracking scheme done by R. Dent to produce image for characterizing fiber orientation varying different parameters in nonwoven structure[22].

2.4. Incorporation of crimp

Most real nonwovens have fibers or filaments with crimp or curl. For simplicity, we assume a sine wave to be sufficient for describing crimp. A sine wave is also convenient because it can be easily represented by its wavelength and amplitude. In defining crimp, we allow crimp percentage and period (wavelength) to be specified. The height (amplitude) is computed from these parameters[29-31].

3. Orientation Distribution Function (ODF)

The orientation distribution function (ODF) f(α) is a function of the angle α. The integral of the function f (α) from an angle a α₁ to a α₂ is equal to the probability that a fiber will have an orientation between the angles α₁, and a₂. The function f(α) must additionally satisfy the following conditions (7) and (8);

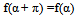(7)

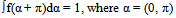(8)

The simulation ODF is computed while the simulation is in progress depending on the segment size for crimped fibers[27,31].

3.1. Simulation Results

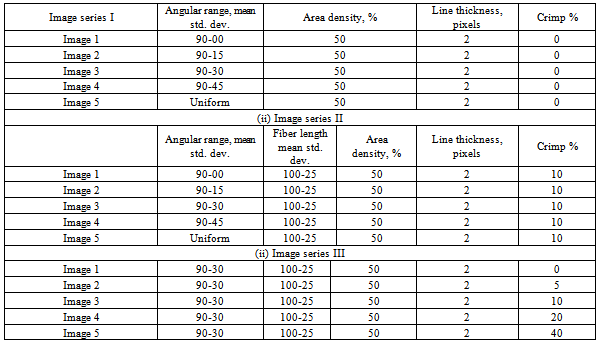
Some sample results are presented in Tables 4 show the structural features of the simulated images. Table 4. (i) displays image series I where the orientation anisotropy varies for a set composed of continuous lines with no crimp. They were generated using the μ-randomness procedure. All other parameters were kept constant for this series. Table 4 (ii) shows the image series II also vary in their orientation anisotropy. These are composed of discontinuous lines and incorporate 10% crimp[32]. They were generated using the I-randomness procedure. The third series was also generated using the I-randomness procedure and they vary only in their crimp percentage, shown in Table 4.

3.2. Frequency Distribution Curve

In each series there were five images taken by the author varying their orientation angular range, and the different series were made varying their crimp level that is at zero crimp level (continuous) and particular crimp level (staple 10%) and different crimp level. Here we give three images of different orientation range of two distinct series that is at no crimp and at 10% crimp. From the curve we clearly see that keeping same parameters in both cases, only due varying their crimp level the shape of the curve changes, that is likely from unimodal to bimodal, the cause of this may be crimp effect[26-27].

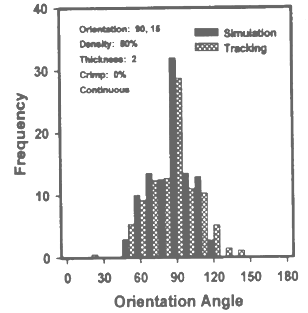Figure 6. ODF of Series I, image 2, at 0% crimp

The results for image series I and II (continuous filament and staple) are shown in Figures for varying anisotropy due to crimp, where the frequencies recorded during simulation (in black) are compared to the values found in tracking (in dotted).

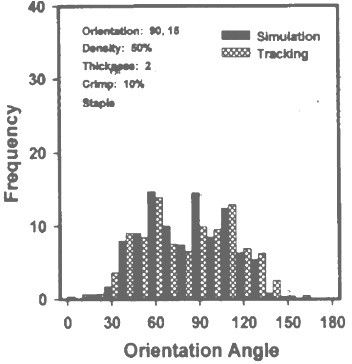Figure 7. ODF of Series II, image 2, at10% crimp[26]

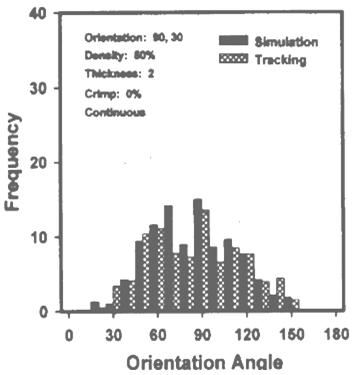Figure 8. ODF of Series II, image 3, at 0% crimp

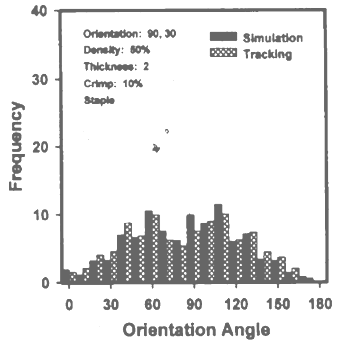Figure 9. ODF of Series III, image 3, at10% crimp[27]

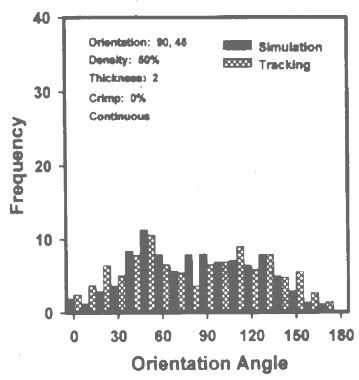Figure 10. ODF of Series I, image 4, at 0% crimp

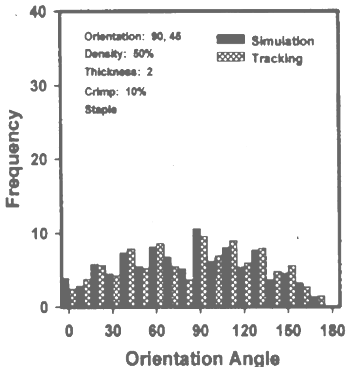Figure 11. ODF of Series III, image 4, at 10% crimp[26]

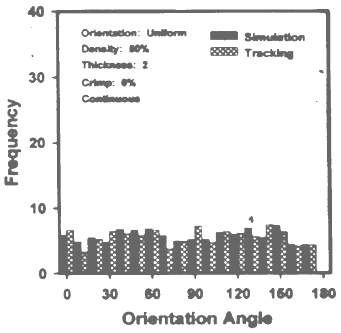Figure 12. ODF of Series I, image 5, at 0% crimp

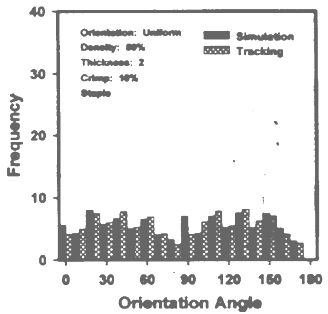Figure 13. ODF of Series II, image 5, at 10% crimp[27]

4. Conclusions

The influence of on single fiber crimp characteristics is being reviewed in this study. Stress-strain data in the crimp removal region are being collected with the Textechno FAVIMAT. Due to very high variability, a statistically reliable correlation between processing parameters and fiber crimp characteristics as determined with the Textechno software could not be established yet. Parameters characterizing the shape of the stress-strain curve in the crimp region rather than single points of the curve seen more suitable to describe fiber crimp characteristics and will hopefully reduce the variability[36]. A general function that fits the experimental stress-strain data in the crimp region of several different fibers has been found. The general validity of this model function is being investigated and the two shape parameters of the fitting curve are being evaluated quantitatively for various fibers. Based on this function and the previously introduced mechanical model for the crimp removal mechanism, a characteristic function for the torsional spring moment in the crimp node can be derived. In nonwoven, crimp and crimp retention of synthetic fibers during processing are, along with finish, major contributors to processing efficiency, web cohesion, fabric bulk and bulk stability[33-35]. The meaning of measurable crimp parameters and their influence on processing and fabric characteristics has not been quantified. Experimental stress-strain data from the Textechno FAVIMAT are being analyzed to determine appropriate parameters for the characterization of crimp and crimp stability and for the prediction of processing and fabric characteristics.