-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2012; 2(6): 175-180
doi:10.5923/j.fs.20120206.07
Applying of Fuzzy Logic Interface in Nylon Fiber Production
Kunal Singha1, Subhankar Maity1, Mrinal Singha2
1Department of Textile Technology, Indian Institute of Technology, Delhi, India
2Department of Pharmaceutical Chemistry, CU Shah College of Pharmacy & Research, Gujarat, India
Correspondence to: Kunal Singha, Department of Textile Technology, Indian Institute of Technology, Delhi, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The nylon fiber by its high strength and modulus is becomes a potential option for many applications like general technical textile, high performance uses, nanotechnology material as a reinforced composite formulation and nanocrisper. The production of nylon fiber can be easily predicted and perform at an accurate level of energy saving with the help of using fuzzy logic interface. The circulation of hot/cold oil flow which has normally used as the fuel to increase the temperature of the nylon fiber reactor can be precisely checked by fuzzy logic data. The pressure and temperature of the reactor can be also controlled by this process of adding fuzzy intelligence or simulation in the chamber of the nylon fiber production reactor.
Keywords: Nylon Fiber, Fuzzy Logic Interface, Hot/Cold Oil Flow, Temperature, Pressure, Fuzzy Intelligence, Simulation
Cite this paper: Kunal Singha, Subhankar Maity, Mrinal Singha, Applying of Fuzzy Logic Interface in Nylon Fiber Production, Frontiers in Science, Vol. 2 No. 6, 2012, pp. 175-180. doi: 10.5923/j.fs.20120206.07.
Article Outline
1. Introduction
- Fuzzy logic is a form of multi-valued logic derived from fuzzy set theory to deal with reasoning that is approximate rather than precise. Several studies1,2,3,4 are conducted using a fuzzy approach in order to simulate, predict and evaluate textile structure properties. In fact, several advantages make fuzzy logic theory among the tools of forecast which are most used by researchers. Altinoz1 suggests that fuzzy logic is an enabling technology that can be used to capture expertise and compute using linguistic rules for supplier selection. Usually, the fuzzy logic method is based on four essential steps. First, fuzzification consists to convert the feature values of input and output parameters. Second, design of the fuzzy rules to implement the model for prediction. Third, the fuzzified values are then inferred to provide decisions by the inference engine with the support of the fuzzy rule base. Finally selection by defuzzification converts fuzzy sets into a crisp value3. There are five built-in methods supported: centroid (used on our study), bisector, medium-maximum (the average of the maximum value of the output set), high-maximum and low-maximum. In this paper we deals with how to maximise production of nylon fiber by using fuzzy logic technique at a optimum energy supply.Batch and semi-batch polymerization are typical of some processes such as PVC (poly vinyl chloride) and nylon production. The difficulty of measuring controlled variables, the existence of interactions, dead time and constraints, added to the nonlinear and multivariable nature of the system, pose challenging problems for the control of polymerization reactors for the batch and semi-batch reactors in particular, additional difficulties arise concerning process variables, such as reactor temperature and pressure, which have to follow set-point trajectories to assure the quality of the final product. In some cases, control is achieved using an open loop control approach. Mainly we use fuzzy logic application in semi –batch process in case of nylon 6 polymerization 5,6.
2. Fuzzy Control in Nylon 6 Semi Batch
- The process comprises a semi-batch reactor (V-tube) for the production of nylon 6 (2.7 m3 volume)5, equipped with stirrer and jacket, where hot oil or cold oil flow (not simultaneously) promotes heating or cooling of the reaction mass. One complete batch takes about 6 hr to complete6. At the first stage- caprolactam and water are feed into the reactor. The reaction is endothermic initially and the reaction mass has to be heated for 3 hr from the initial temperature (90℃) up to 260℃. At this point, the - caprolactam rings open, resulting in amino-caproic acid formation. Over the following 3 hr, the reactor temperature is maintained at 260℃ and the polyaddition reaction (exothermic reaction) of the aminocaproic acid takes place. As a result the reaction mass becomes overheated causing liquid desorption from the free surface and desorption through bubble formation resulting in water vaporization and also vaporization of a small amount of caprolactam. Subsequently the initial pressure of 2 atm is increased for 3 hr to reach the required 5 atm pressure and this is maintained for a further hour. After this a pressure reduction procedure starts up to reach atmospheric pressure. A vacuum pump is then started and depressurization begins for 1 hr, reaching 420 mmHg. The polymer is immediately discharged from the reactor, solidified with cool water and set out for drying and palletizing processes7,8,10.The main problem is here is that to maitain a proper temperature(260℃) and pressure (2 atm) becouse of the control problem is typically a set-point tracking or servo problem and the reaching of these specified requirements is of great importance to assure the desired quality of the final product. we can solve this problem by using a flow of hot /cold oil through around the VK-tube used with the help of fuzzy logic8.
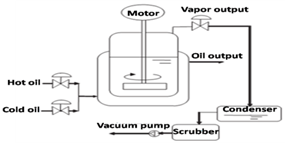 | Figure 1. Semi-batch reactor for theproduction of nylon 6 (heating and cooling system)8 |
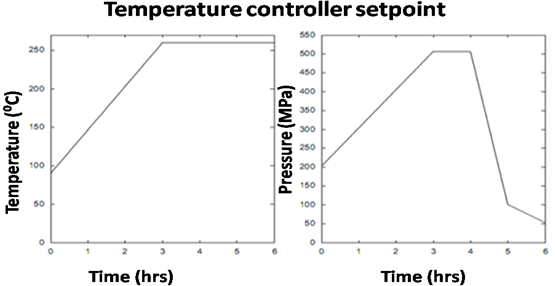 | Figure 2. Set-point trajectories for temperature and pressure8 |
3. Kinetic and Mathematic Modeling
- The equations of the phenomenological model adopted in this work by uses the following assumptions9• Heat transfer occurs from the hot oil inside the jacket to the reaction mass in the heating step and from the reaction mass to the cold oil in the cooling step.• Water and - caprolactam vaporization from the reaction mass. • Pressure build-up due to the heating process. • Variable viscosity of the reaction medium during the batch and its effects on the mass and energy transfer coefficients. • Mass and energy balances of the system.
- The following kinetic model was considered:Ring opening reaction of the - caprolactam (C1) monomer, with the amino- caproic acid (S1) formation (W refers to water)1,8
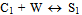 | (1) |
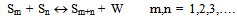 | (2) |
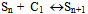 | (3) |
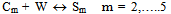 | (4) |
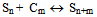 | (5) |
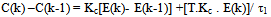 | (6) |
 So rewrittening the eqn. (6) we can get:
So rewrittening the eqn. (6) we can get: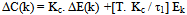 | (7) |
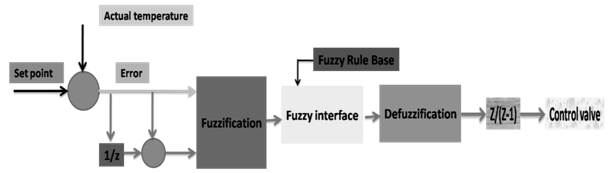 | Figure 3. PI fuzzy controller diagram1 |
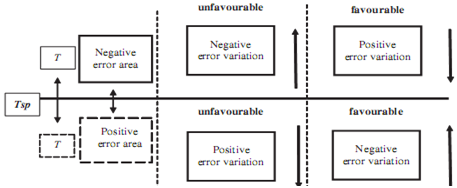 | Figure 4. Configurations for the error and the error variation (temperature control)3 |
4. Fuzzy Control Design
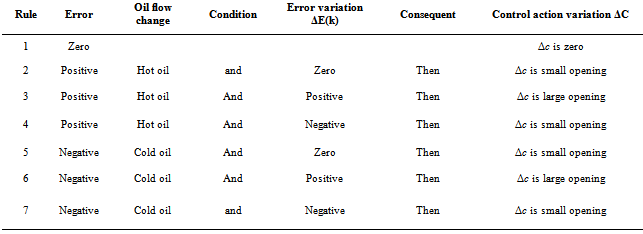
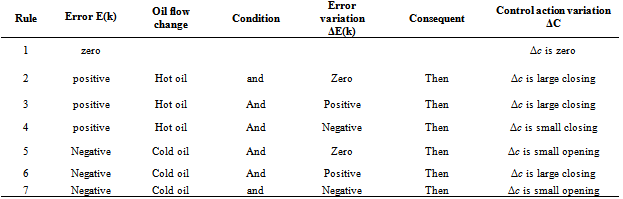
- The fuzzy inference system adopted in this work is based on the Mamdani model based on human analyzing power for a given situation how far is closed to the real phenomenan. In case of controlling the temperature and pressure in nylon 6 polymerization we can get the following errors like: Zero error, Positive error, Negative error, Zero error variation, Positive error variation, Negative error variation, Great control action variation, Small control action variation, Zero control action variation 13,14,17.
|
|
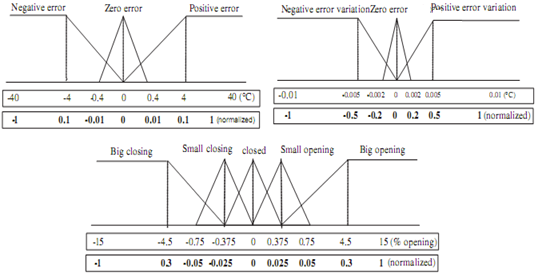 | Figure 5. Membership functions of error, error variation and control action variation (temperature fuzzy control)15 |
 | Figure 6. Split range configuration for oil flowing17 |
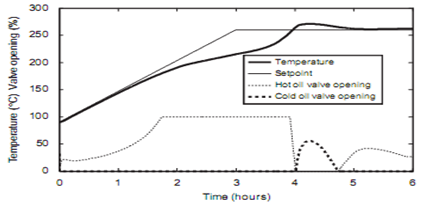 | Figure 7. Temperature and manipulated variables (conventional PID control)17 |
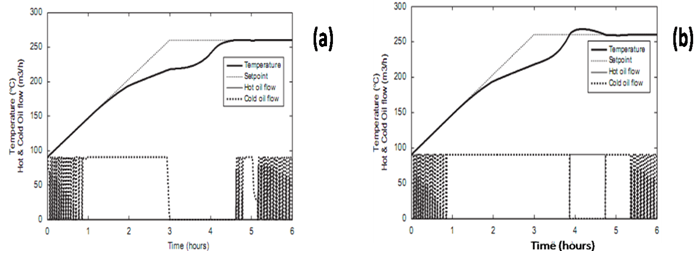 | Figure 8. (a) Temperature and manipulated variables (PI-fuzzy control) (without anticipatory action) and (b) Temperature and manipulated variable (PI-fuzzy control) (with anticipatory action)16 |
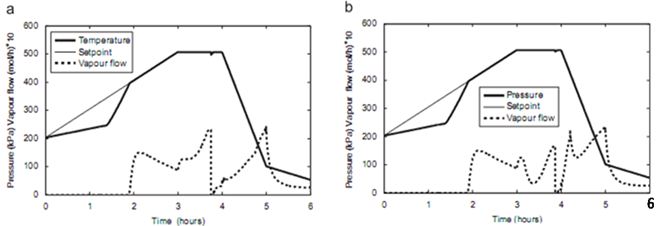 | Figure 9. (a) Pressure and manipulated variable (PI-fuzzy control) (without anticipatory action) and (b) pressure and manipulated variable (PI-fuzzy control) (with anticipatory action, Table 2)18 |
5. Concluding Remarks
- Nylon is an important fiber in today’s world because of its highly rigid but suitable structure for most of the processing later. In this current review we have predicted the best energy saving model for nylon 6 polymerization spinning process by applying fuzzy modeling19,20,21,22. Indeed, the results also show that the change of fuzzy membership function affects the prediction accuracy of the rate of polymerization. Compared to experimental results, it may be concluded that, overall, theoretical models using fuzzy technique are marked by relatively acceptable correlation coefficients especially using triangular membership function23,24. Traditional methods are limited to evaluating bagging appearance by single parameters such as oil flow, rate of the reaction etc. which cannot represent the abundant information given by the appearance reactor system11,23. The error values between analytical and experimental results within and without fuzzy system show the effectiveness of the fuzzy forecast model25,26. Thanks to the fuzzy interface technique, we could make possible the forecast of the value of the nylon 6 reactor processing exactly during the manufacturing of the polymer.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML