-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2012; 2(6): 159-168
doi: 10.5923/j.fs.20120206.05
Central Field in Rotating Spherical Space in 5D
Wladimir Belayev
Center for Relativity and Astrophysics, 185 Box, 194358, Saint-Petersburg, Russia
Correspondence to: Wladimir Belayev, Center for Relativity and Astrophysics, 185 Box, 194358, Saint-Petersburg, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A time-like geodesic motion in rotating 5D space is studied in framework of Kaluza-Klein theory and astrophysical applications are proposed. For example of such space-time in 4D spherical coordinates with the space-like fifth dimension a transition to the cylindrical frame is implemented. After this transformation a space is divided into two parts that is interpreted physically as pair of the universe and anti-universe. The rotation in 5D space-time exhibits itself in 4D as action of extra force, which reveals itself with observed radial motion of the material particle. Also it is considered similar (3+2)D space-time in which additional dimension is time-like and a motion of space is hyperbolic. For these space-times it is found geodesics with constant radius in 4D spherical coordinates and studied their small deviations in cylindrical frames. It is shown that model with space-like fifth coordinate conforms to the basic properties of the Pioneer-effect, namely, a) constant additional acceleration of apparatus on distance from 20 to 50 a.e., b) its increase from 5 to 20 a.e., c) observed absence of one in motion of planets.
Keywords: Time-Like Geodesics, Kaluza-Klein Theory, Pioneer-Effect
Cite this paper: Wladimir Belayev, "Central Field in Rotating Spherical Space in 5D", Frontiers in Science, Vol. 2 No. 6, 2012, pp. 159-168. doi: 10.5923/j.fs.20120206.05.
Article Outline
1. Introduction
- A five-dimensional model of the space-time was proposed by Nordstrom[1] and Kaluza[2] for unity of gravitation and electromagnetism. Klein[3] suggested a compactification mechanism, owing to which internal space of the Planck size forms additional dimension. In his theory a motion of particle having rest mass in 4D can be described by equations of null geodesic line in 5D, which are interpretation of massless wave equation with some conditions.In development of this model 5D space-time is considered as low energy limit of more high-dimensional theories of supersymmetry, supergravity and string theory. They admit scenario, in which particle has a rest mass in 5D[4, 5]. Exact solutions of Kaluza-Klein and low limit of bosonic string theories in 5D-6D[6] with toroidal compactification are equivalent. Analogous conclusion is made in[7] with comparison space-time-mass theory based on geometric properties of 5D space without compactification and braneworld model. Predictions of five-dimensional model of extended space and its experimental tests are considered in[8, 9]. Cosmological model with motion of matter in fifth dimension also is examined[10]. Astrophysical applications of braneworld theories, including Arkani-Hamed- Dimopoulos-Dvali and Einstein-Maxwell models with large extra dimensions, are analyzed in[11]. EM model in 6D has become further development in[12], where linear perturbations sourced by matter on the brane are studied.In[13] it is proposed low energy effective theory on a regularized brane in 6D gauged chiral supergravity. A possibility of the orbits of particles around the extra dimesions in (4+n)D space, periodically returning in 4D surface, is phenomenologically predicted in ADD model[14]. Phenomena, described by one-time physics in 3+1 dimensions, appear as various "shadows" similar phenomena that occur in 4+2 dimensions with one extra space and one extra time dimensions (more generally, d+2)[15, 16, 17].In present paper it is considered some geometrical construction in (4+1)D space-time with space-like fifth dimension and rotation in 4D spherical coordinates with transition thereupon to the standard cylindrical frame. It is studied also (3+2)D space-time with time-like additional dimension, where the motion is hyperbolic.A motion of the particle in certain domain of space in appropriate coordinates is assigned to be described with sufficient accuracy by geodesic equations. Their solutions lead to conclusion that rotation in 5D space-time exhibits itself in 4D as action of central force.In astrophysical applications proposed model of space-time is of interest with respect to Pioneer effect. In some papers[18, 19], see also review of efforts to explain anomaly[20], presence of signal frequency bias is associated with dependence of fundamental physical parameters from time. Though it should allow for data[21], which witness independence of direction of additional acceleration from route of radial motion with respect to Sun. A radial Rindler-like acceleration[22, 23] in itself also can't explain the Pioneer effect because it is absent in planets motion[24].
2. Geodesics in Rotating Space
- Five-dimensional space-time having 4D spherical symmetry is considered in coordinate frame
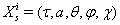 , where
, where 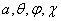 are spherical space coordinates and
are spherical space coordinates and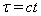 , where
, where 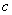 is light velocity constant and
is light velocity constant and 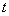 is time. Rotating space-time with space-like fifth dimension[25] is described by metric
is time. Rotating space-time with space-like fifth dimension[25] is described by metric 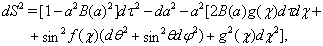 | (1) |
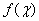 is continuously increasing and it is taken
is continuously increasing and it is taken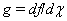 . For the domain under review it is assumed
. For the domain under review it is assumed 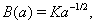 | (2) |
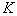 is constant.Transition to five-dimensional cylindrical coordinates
is constant.Transition to five-dimensional cylindrical coordinates 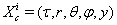 for
for 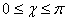 is performed by transformation
is performed by transformation 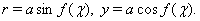 | (3) |
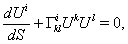 | (4) |
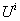 are components of five-velocity vector and
are components of five-velocity vector and 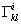 are 5D Christoffel symbols of second kind. In spherical coordinates for metric (1) these equations, with
are 5D Christoffel symbols of second kind. In spherical coordinates for metric (1) these equations, with 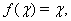 | (5) |
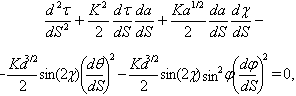 | (6) |
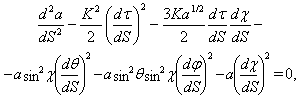 | (7) |
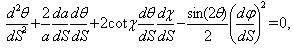 | (8) |
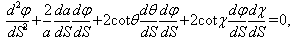 | (9) |
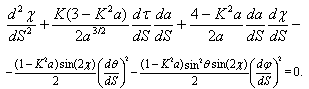 | (10) |
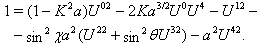 | (11) |
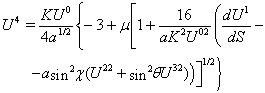 | (12) |
 is
is  . We name corresponding solutions as a solution of type I with
. We name corresponding solutions as a solution of type I with  and as a solution of type II with
and as a solution of type II with 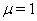 .When particles move along geodesics, which are arcs of circle:
.When particles move along geodesics, which are arcs of circle: 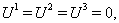 | (13) |
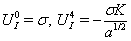 | (14) |
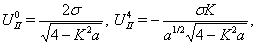 | (15) |
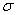 is
is 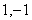 .Change of passage of time is defined as relation between intervals of proper time
.Change of passage of time is defined as relation between intervals of proper time 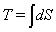 and coordinate time
and coordinate time 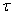 .For geodesic of type I for solution (14) chosen
.For geodesic of type I for solution (14) chosen 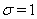 we have
we have 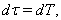 | (16) |
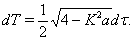 | (17) |
3. Representation in Cylindrical Frame
- After substitutions of coordinate transformation being inverse to (3), namely,
 | (18) |
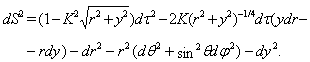 | (19) |
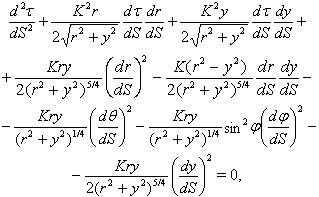 | (20) |
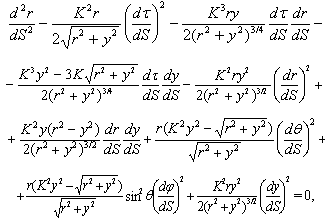 | (21) |
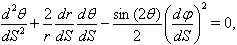 | (22) |
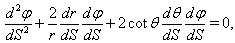 | (23) |
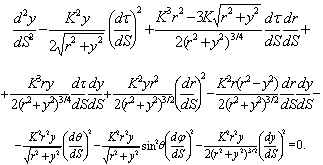 | (24) |
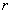 and
and 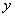 are found by differentiation of transformations (3) and will be
are found by differentiation of transformations (3) and will be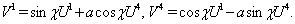 | (25) |
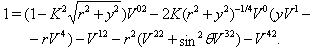 | (26) |
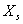 (13)-(15) are rewritten in coordinate frame
(13)-(15) are rewritten in coordinate frame 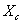 as
as 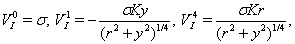 | (27) |
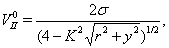 | (28) |
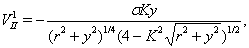 | (29) |
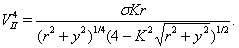 | (30) |
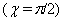 they correspond with stationary in 4D particle.For motion in the neighborhood of point
they correspond with stationary in 4D particle.For motion in the neighborhood of point 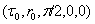 with
with 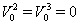 geodesic equations are reduced to
geodesic equations are reduced to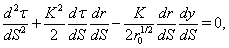 | (31) |
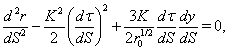 | (32) |
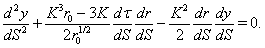 | (33) |
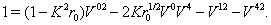 | (34) |
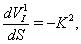 | (35) |
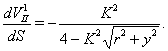 | (36) |
4. Metrics with Time-Like Fifth Coordinate
- A space-time with 4D spherical coordinates
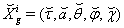 having hyperbolic motion is described by metric
having hyperbolic motion is described by metric 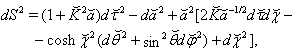 | (37) |
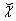 is assumed to be time-like and
is assumed to be time-like and 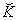 is constant. This metric can be obtained from (1) for (2), (5) by substitution
is constant. This metric can be obtained from (1) for (2), (5) by substitution 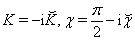 and addition of (˘) in the notation of other coordinates.The geodesics equations for a particle motion along time-like path are
and addition of (˘) in the notation of other coordinates.The geodesics equations for a particle motion along time-like path are 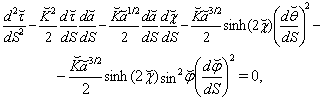 | (38) |
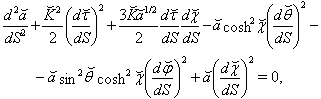 | (39) |
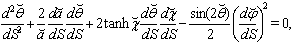 | (40) |
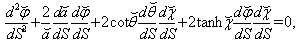 | (41) |
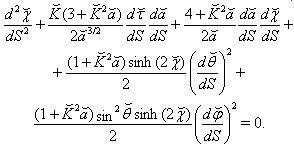 | (42) |
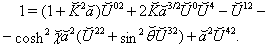 | (43) |
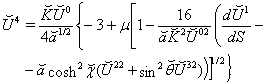 | (44) |
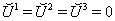 corresponding five-velocity vectors have non-zero components
corresponding five-velocity vectors have non-zero components 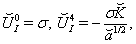 | (45) |
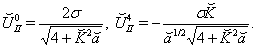 | (46) |
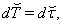 | (47) |
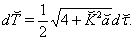 | (48) |
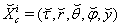 is realized by transformation
is realized by transformation 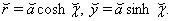 | (49) |
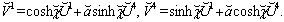 | (50) |
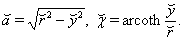 | (51) |
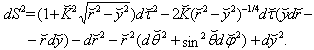 | (52) |
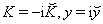 and addition of (˘) in the notation of other coordinates in (19).Geodesics equations for motion of particle having rest mass are written as
and addition of (˘) in the notation of other coordinates in (19).Geodesics equations for motion of particle having rest mass are written as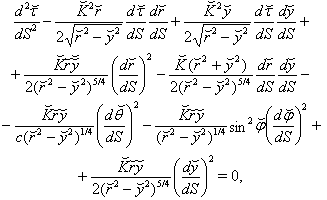 | (53) |
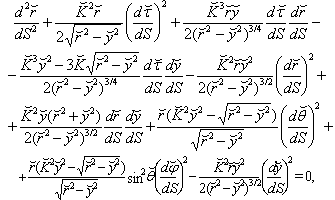 | (54) |
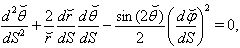 | (55) |
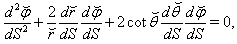 | (56) |
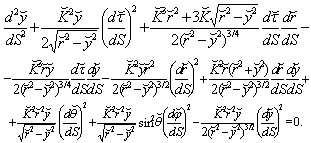 | (57) |
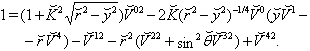 | (58) |
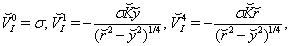 | (59) |
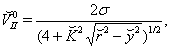 | (60) |
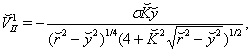 | (61) |
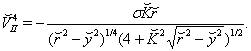 | (62) |
 with
with  local solution is found from reduced Eqs. (53)-(57), which turned out to
local solution is found from reduced Eqs. (53)-(57), which turned out to 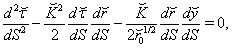 | (63) |
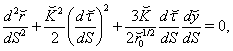 | (64) |
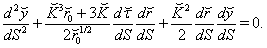 | (65) |
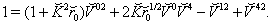 | (66) |
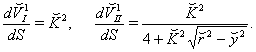 | (67) |
5. Kaluza-Klein Model
- In Kaluza-Klein theory the line element is brought in form
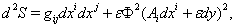 | (68) |
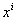 and
and 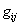 are coordinates and metrical tensor of 4D space-time,
are coordinates and metrical tensor of 4D space-time, 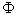 and
and 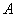 are scalar and vector potential. Metrical coefficients and potentials are functions of
are scalar and vector potential. Metrical coefficients and potentials are functions of 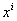 and y. Constant
and y. Constant 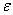 equals 1 for time-like fifth coordinate y and -1, when it is space-like.In this form metrics (19) and (52) are represented by line-element of 4D space-time
equals 1 for time-like fifth coordinate y and -1, when it is space-like.In this form metrics (19) and (52) are represented by line-element of 4D space-time 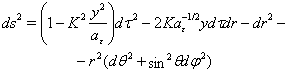 | (69) |
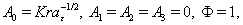 | (70) |
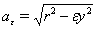 .If 4D metric satisfies cylindrical conditions
.If 4D metric satisfies cylindrical conditions 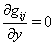 ratio of electric charge to mass in 4D is written as
ratio of electric charge to mass in 4D is written as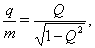 | (71) |
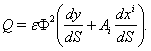 | (72) |
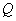 and
and 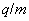 is not identical[4], but value
is not identical[4], but value 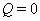 also corresponds to
also corresponds to 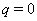 .For considering space-time after substituting components of the found five-velocity vectors of the type I (27) and (59) we obtain
.For considering space-time after substituting components of the found five-velocity vectors of the type I (27) and (59) we obtain 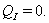 | (73) |
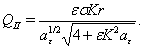 | (74) |
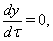 | (75) |
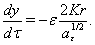 | (76) |
6. Astrophysical Applications
- Considering phenomenology of particles motion in 5D we assume that stationary in 3D space particles, having rest mass, move in spherical or hyperbolic frames in 5D along geodesics with constant radial coordinate: Eqs. (14), (15) and (27)-(30) or Eqs. (45), (46) and (59)-(62). It is suggested also that in cylindrical frame the matter moves along fifth coordinate in single direction, which is opposite to the antimatter motion.In case of the space-like fifth dimension the function
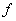 from metric (1) is chosen so that its meaning is continuously increasing in intervals
from metric (1) is chosen so that its meaning is continuously increasing in intervals 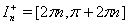 for integer
for integer 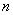 . Since value
. Since value 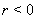 is inadmissible in cylindrical frame we must assume that function
is inadmissible in cylindrical frame we must assume that function 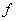 has discontinuity on the endpoints of
has discontinuity on the endpoints of 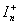 , which prescribes singularity. It can be avoided if model of binary world consisting of the universe - anti-universe pair[26-28] is considered under the assumption that it possesses a large number of copies[29, 30], in which a physical laws are identical. In bulk a space-time half
, which prescribes singularity. It can be avoided if model of binary world consisting of the universe - anti-universe pair[26-28] is considered under the assumption that it possesses a large number of copies[29, 30], in which a physical laws are identical. In bulk a space-time half 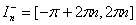 put into accordance with packet of 4D anti-universes. With condition (5) the intervals
put into accordance with packet of 4D anti-universes. With condition (5) the intervals 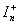 ,
, 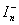 contain values of additional coordinate
contain values of additional coordinate  . Rotation of one particle with transition to cylindrical coordinates should be interpreted as motion of particle and anti-particle through opposite packets of branes, which conforms to CPT-symmetry of the universe and anti-universe. Thus a birth of the pair particle-antiparticle is assumed to occur in points
. Rotation of one particle with transition to cylindrical coordinates should be interpreted as motion of particle and anti-particle through opposite packets of branes, which conforms to CPT-symmetry of the universe and anti-universe. Thus a birth of the pair particle-antiparticle is assumed to occur in points 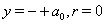 , after which they move through opposite packets of branes and annihilate, when
, after which they move through opposite packets of branes and annihilate, when 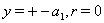 .
.6.1. Basic Properties of the Pioneer Effect Model
- Recently much attention was attracted to the Pioneer effect, which consists in additional acceleration of spacecrafts Pioneer 10/11[20, 24, 31, 32]
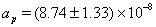 cm s
cm s at dictances 15-45 AU directed to the Sun[33]. We will analyze how much studying models of rotating space conform to this data. Motion of the spacecrafts and the planets will be considered in the frame of the Sun.For this analysis we must use geodesics of the type I because, as it was shown in Sec. 5, for geodesics with constant radial coordinate they correspond to the neutrally charged particles. Their proper time coincides with coordinate time for trajectories, which are the arcs of circle (16) or hyperbola (47). Also motion of light is assumed to correspond with equation (75), i.e. a light shift along the fifth coordinate is absent.In the Sun's gravity field motion of the particle with rest mass is described approximately by equations
at dictances 15-45 AU directed to the Sun[33]. We will analyze how much studying models of rotating space conform to this data. Motion of the spacecrafts and the planets will be considered in the frame of the Sun.For this analysis we must use geodesics of the type I because, as it was shown in Sec. 5, for geodesics with constant radial coordinate they correspond to the neutrally charged particles. Their proper time coincides with coordinate time for trajectories, which are the arcs of circle (16) or hyperbola (47). Also motion of light is assumed to correspond with equation (75), i.e. a light shift along the fifth coordinate is absent.In the Sun's gravity field motion of the particle with rest mass is described approximately by equations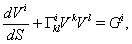 | (77) |
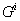 is Schwarzschild-like force vector and left terms correspond to Eqs. (20)-(24) or (53)-(57). Denoting acceleration
is Schwarzschild-like force vector and left terms correspond to Eqs. (20)-(24) or (53)-(57). Denoting acceleration 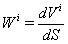 we divide it into
we divide it into 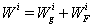 , where vector
, where vector 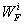 conforms in case
conforms in case 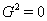 ,
, 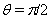 in the neighborhood of point
in the neighborhood of point 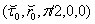 to equations
to equations 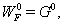 | (78) |
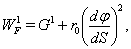 | (79) |
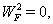 | (80) |
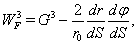 | (81) |
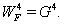 | (82) |
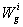 correspond to Eqs. (31)-(33) or (63)-(65).By using analogy with motion of particle in central gravity field in 4D, we take
correspond to Eqs. (31)-(33) or (63)-(65).By using analogy with motion of particle in central gravity field in 4D, we take 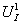 and
and 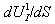 for
for 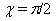 in spherical coordinates or
in spherical coordinates or 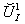 and
and 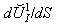 for
for 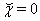 in hyperbolic coordinates as radial velocity and acceleration observed in 4D surface of five-dimensional space-time.
in hyperbolic coordinates as radial velocity and acceleration observed in 4D surface of five-dimensional space-time.6.2. Model with Space-Like Fifth Coordinate
- In spherical coordinates in the neighborhood of point
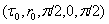 Eqs. (31)-(33) correspond to system (6)-(10) reduced to
Eqs. (31)-(33) correspond to system (6)-(10) reduced to 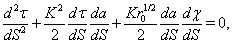 | (83) |
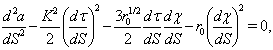 | (84) |
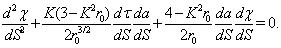 | (85) |
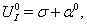 | (86) |
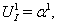 | (87) |
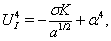 | (88) |
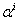 are functions of coordinates. Substitution of
are functions of coordinates. Substitution of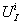 in (83)-(85) yields
in (83)-(85) yields 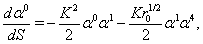 | (89) |
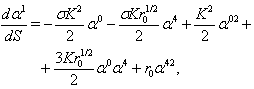 | (90) |
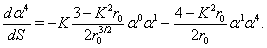 | (91) |
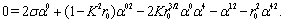 | (92) |
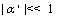 and assume
and assume 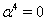 on the surface
on the surface 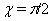 . First and second equations of system (89)-(91) reduce to
. First and second equations of system (89)-(91) reduce to 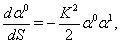 | (93) |
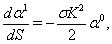 | (94) |
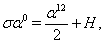 | (95) |
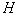 is constant. Substituting this expression into Eq. (94) and choosing
is constant. Substituting this expression into Eq. (94) and choosing 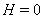 we obtain
we obtain 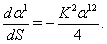 | (96) |
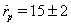 km s
km s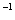 (See diagram in[24]) and for approximation
(See diagram in[24]) and for approximation 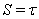 it approximately corresponds to
it approximately corresponds to 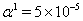 . Therefore this equation turns out to be
. Therefore this equation turns out to be 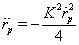 | (97) |
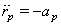 yields
yields 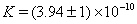 cm
cm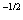 . For this value and made choice of
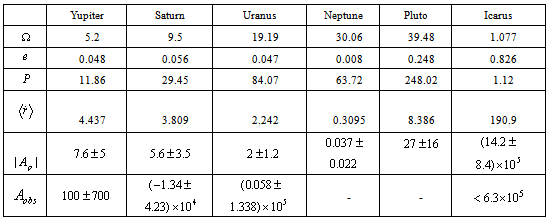
. For this value and made choice of 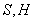 , Eq. (95) conforms to (92) without small higher-order terms.Additional acceleration of Pioneer 11 and its predicted magnitude are contained in Table 1 .
, Eq. (95) conforms to (92) without small higher-order terms.Additional acceleration of Pioneer 11 and its predicted magnitude are contained in Table 1 .
|
6.3. Additional Acceleration of Planets
- In this section we will test proposed model by finding additional acceleration for planets of the solar system and comparing them with observations data. Further we will use following denotations:
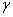 is gravity constant,
is gravity constant, 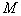 is the Sun's mass,
is the Sun's mass, 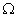 is its semimajor axis,
is its semimajor axis, 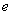 is eccentricity,
is eccentricity, 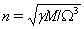 is unperturbed Keplerian mean motion,
is unperturbed Keplerian mean motion, 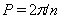 is orbital period and
is orbital period and 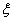 is eccentric anomaly.
is eccentric anomaly.- Parameters of motion are given by equations
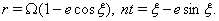 | (98) |
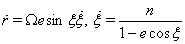 | (99) |
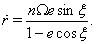 | (100) |
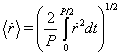 | (101) |
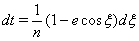 | (102) |
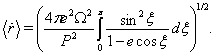 | (103) |
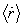 for the planets, corresponding them Pioneer-like acceleration
for the planets, corresponding them Pioneer-like acceleration 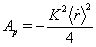 | (104) |
 , obtained from observations are in Table 2 . Predicted additional radial acceleration for Yupiter, Saturn, Uranus is within the observation error and for asteroid Icarus it is close to upper limit of
, obtained from observations are in Table 2 . Predicted additional radial acceleration for Yupiter, Saturn, Uranus is within the observation error and for asteroid Icarus it is close to upper limit of  .
.6.4. Model with Time-Like Fifth Coordinate
- In hyperbolic coordinates in the neighborhood of point
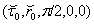 Eqs. (63)-(65) correspond to system (38)-(42) reduced to
Eqs. (63)-(65) correspond to system (38)-(42) reduced to 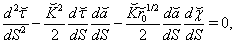 | (105) |
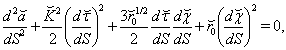 | (106) |
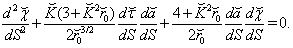 | (107) |
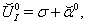 | (108) |
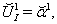 | (109) |
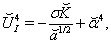 | (110) |
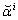 are functions of coordinates. Substitution of
are functions of coordinates. Substitution of 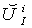 in (105)-(107) yields
in (105)-(107) yields 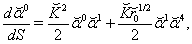 | (111) |
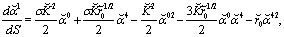 | (112) |
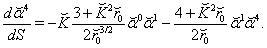 | (113) |
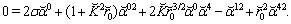 | (114) |
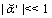 and assume
and assume 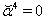 on the surface
on the surface 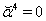 . Equations (111), (112) reduce to
. Equations (111), (112) reduce to 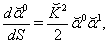 | (115) |
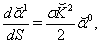 | (116) |
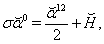 | (117) |
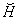 is constant. Substituting this expression into Eq. (116) we obtain
is constant. Substituting this expression into Eq. (116) we obtain 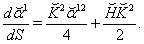 | (118) |
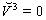 in point
in point 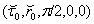 from Eq. (64) we obtain
from Eq. (64) we obtain 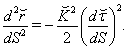 | (119) |
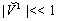 , this equation conforms to unmodeled acceleration of Pioneer 10/11 on distance 20-50 a.e., but gives the same acceleration for Pioneer 11 on distance less than 20 a.e. and for planets of the Sun system that contradicts data of observations (Tables 1,2).
, this equation conforms to unmodeled acceleration of Pioneer 10/11 on distance 20-50 a.e., but gives the same acceleration for Pioneer 11 on distance less than 20 a.e. and for planets of the Sun system that contradicts data of observations (Tables 1,2).7. Conclusions
- Proposed toy-model of space is based on idea of double manyfold Universe. It is supported by notion that closed geodesic of elementary particle having a rest mass corresponds to motion of the pair particle-antiparticle in the mirror worlds.Found solutions of geodesics equations corresponding to the particle with a rest mass for cosiderig space-times describe motion in a circle with space-like fifth coordinate and hyperbolic motion with time-like fifth coordinate. Time dilation is absence for the solutions corresponded in the Kaluza-Klein model to neutrally charged particle. In this case the angular velocity is inversely proportional to the square root of radius in spherical coordinates. In astrophysical applications the center of the Sun has been chosen as the center of this motion. Analogy with motion in central gravity field in 4D is employed for determination of velocity and acceleration observed in 4D sheet for particles moving in 5D bulk. We obtain approximate solution in the neighborhood of surface with zero fifth coordinate in cylindrical frame for geodesics deviating from having constant radius. With space-like fifth coordinate a body in included 4D space-time with limited velocity will have centripetal acceleration being proportional to square of radial velocity and directed towards center of rotaion of space in 5D. This acceleration is interpreted as action of additional force in 4D. That roughly corresponds to underlying properties of the Pioneer-effect, such as constant additional acceleration of apparatus towards the Sun on distance from 20 to 50 a.e., its increase from 5 to 20 a.e., observed absence of one in motion of planets. However, presence of analogous acceleration in motion of bodies with similar radial velosity, for example, asteroid Icarus, will be significant for confirmation of this model. In case of space-time with time-like fifth coordinate it isn’t found geodesics corresponding to this effect.
References
| [1] | G. Nordstrom, “Uber die Moglichkeit, das Electromagnetishe Feld und das Gravitation Feld zu Vereinigen”, Phyz. Zeitschr., Vol. 15, 504-506, 1914. |
| [2] | T. Kaluza, “Zum Unitatsproblem der Physik”, Sitz. Preuss. Akad. Wiss. Phys. Math. K, Vol. 1, pp. 966-972, 1921. |
| [3] | O. Klein, “Quantentheorie und funfdimensionale Relativitatstheorie”, Z. Phys., Vol. 37, pp. 895-906, 1926. |
| [4] | J. M. Overduin and P.S. Wesson, “Kaluza-Klein Gravity”, Phys. Rept., Vol. 283, NoNo. 3-4, pp. 303-380, 1997, gr-qc/9805018. |
| [5] | J. Ponce de Leon, “Does force from an extra dimension contradict physics in 4D?” Phys. Lett. B, Vol. 523, NoNo. 3-4, 311-316, 2001, gr-qc/0110063. |
| [6] | A. Herrera-Aguilar and O. V. Kechkin, “Bosonic string - Kaluza Klein theory exact solutions using 5D-6D dualities”, Mod. Phys. Lett. A, Vol. 16, No. 1, pp. 29-39, 2001, gr-qc/0101007. |
| [7] | J. Ponce de Leon, “Equivalence Between Space-Time-Matter and Brane-World Theories”, Mod. Phys. Lett. A, Vol. 16, No. 35, pp. 2291-2303, 2001, gr-qc/0111011. |
| [8] | D.Yu.Tsipenyuk, V.A. Andreev, “5-dimensional extended space model”, Presented at 13th General Conference of the European Physical Society: Beyond Einstein - Physics of the 21st Century (EPS-13), Bern, Switzerland, 11-15 Jul 2005. |
| [9] | D.Yu.Tsipenyuk, “Field transformation in the extended space model: Prediction and experimental test”., Gravitation and Cosmology, Vol. 7, No. 4(28), pp. 336-338, 2001. |
| [10] | W. B. Belayev, “Cosmological model with movement in fifth dimension”, Space-time and Substance, Vol. 2, No. 2(7), pp. 63-65, 2001, gr-qc/0110099. |
| [11] | K. Koyama, “The cosmological constant and dark energy in braneworlds”, Gen. Rel. Grav. Vol. 40, NoNo. 2-3, pp. 421-450, 2008, arXiv:0706.1557. |
| [12] | T. Kobayashi and Y. Takamizu, “Hybrid compactifications and brane gravity in six dimensions”, Class. Quant. Grav., Vol.25, No. 1, 015007, 2008, arXiv:0707.0894. |
| [13] | F. Arroja, T. Kobayashi, K. Koyama and T. Shiromizu, “Low energy effective theory on a regularized brane in 6D gauged chiral supergravity”, JCAP, Vol. 2007, No. 12, 006, 2007, arXiv:0710.2539. |
| [14] | N. Arkani-Hamed, S. Dimopoulos, G. Dvali, “The Hierarchy Problem and New Dimensions at a Millimeter”, Phys. Lett. B, Vol.429, NoNo. 3-4, pp. 263-272,1998, hep-ph/9803315. |
| [15] | I. Bars, S.-H. Chen, G. Quelin, “Dual Field Theories In (d-1)+1 Emergent Spacetimes From A Unifying Field Theory In d+2 Spacetime”, Phys. Rev. D, Vol. 76, No. 6, 065016, 2007, arXiv:0705.2834. |
| [16] | I. Bars, S.-H. Chen, “Geometry and Symmetry Structures in 2T Gravity”, Phys. Rev. D, Vol. 79, No. 8, 085021, 2009, arXiv:0811.2510. |
| [17] | I. Bars, “Gauge Symmetry in Phase Space, Consequences for Physics and Spacetime”, Int. J. Mod. Phys. A, Vol. 25, No. 29, pp. 5235-5252, 2010, arXiv:1004.0688. |
| [18] | K. Trencevski, “Time dependent gravitational potential in the universe and some consequences, Gen. Rel. Grav., Vol. 37, No. 3, pp. 507-519, 2005. |
| [19] | W. B., Belayev, “Cosmological model in 5D, stationarity, yes or no”, gr-qc/9903016. |
| [20] | S. G. Turyshev and V. T. Toth, “The Pioneer Anomaly”, Living Rev. Rel., Vol. 13, No. 4, 2010, arXiv:1001.3686. |
| [21] | J. D. Anderson, P. A. Laing, E. L. Lau, A. S. Liu, M. M. Nieto and S. G. Turyshev, “Study of anomalous acceleration of Pioneer 10 and 11”, Phys. Rev. D, Vol. 65, No. 8, 082004, 2002, gr-qc/0104064. |
| [22] | L. Iorio, “Can the Pioneer anomaly be of gravitational origin? A phenomenological answer”, Found. Phys., Vol. 37, No. 6, pp. 897-918, 2007, gr-qc/0610050. |
| [23] | D. Grumiller, “Model for gravity at large distances”, Phys. Rev. Lett., Vol. 105, No. 21, 211303, 2010, arXiv:1011.3625. |
| [24] | L. Iorio, “Solar system constraints on a Rindler-type extra-acceleration from modified gravity at large distances”, JCAP, Vol. 2011, No. 5, 019, 2011, arXiv:1012.0226. |
| [25] | W .B. Belayev, D.Yu. Tsipenyuk, “Gravi-electromagnetism in five dimensions and moving bodies in galaxy area”, Space-time and Substance Vol. 5, No. 2(22), pp. 49-52, 2004, gr-qc/0409056. |
| [26] | A. Linde, “Inflation, Quantum Cosmology and the Anthropic Principle”, in "Science and Ultimate Reality: From Quantum to Cosmos", honoring John Wheeler's 90th birthday. J. D. Barrow, P. C. W. Davies, C. L. Harper eds. Cambridge University Press, 2003, hep-th/0211048. |
| [27] | S. L. Dubovsky, S. M. Sibiryakov, “Domain walls in noncommutative gauge theories, folded D branes, and communication with mirror world”, Nucl. Phys. B, Vol. 691, NoNo. 1-2, pp. 91-110, 2004, hep-th/0401046. |
| [28] | M. Sarrazin, F. Petit, “Equivalence between domain-walls and "noncommutative" two-sheeted spacetimes: Model-independent matter swapping between branes”, Phys. Rev. D, Vol. 81, No. 3, 035014, 2010, arXiv:0903.2498. |
| [29] | N. Arkani-Hamed, S. Dimopoulos, G. Dvali, N. Kaloper, “Manyfold Universe”, JHEP, Vol. 2000, No. 12, 010, 2000, hep-ph/9911386. |
| [30] | G. Dvali, I. Sawicki, A. Vikman, “Dark Matter via Many Copies of the Standard Model”, JCAP, Vol. 2009, No. 8, 009, 2009, arXiv:0903.0660. |
| [31] | J. D. Anderson, P. A. Laing, E. L. Lau, A. S. Liu, M. M. Nieto and S. G. Turyshev, “Indication from Pioneer 10/11, Galileo, and Ulysses data, of an apparent anomalous, weak, long-range acceleration”, Phys. Rev. Lett., Vol. 81, No. 14, pp. 2858-2861, 1998, gr-qc/9808081. |
| [32] | J. D. Anderson and M. M. Nieto, “Search for a Solution of the Pioneer Anomaly”, Contemp. Phys., Vol. 48, No. 1, pp. 41-54, 2007, arXiv:0709.3866. |
| [33] | S. G. Turyshev, M. M. Nieto, J. D. Anderson, “A Route to Understanding of the Pioneer Anomaly”, The XXII Texas Symposium on Relativistic Astrophysics, Stanford U, December 13-17, 2004, edited by P. Chen, E. Bloom, G. Madejski, and V. Petrosian, gr-qc/0503021. |
| [34] | R. H. Sanders, “Solar system constraints on multi-field theories of modified dynamics”, Mon. Not. Roy. Astron. Soc., Vol. 370, No. 3, pp. 1519-1528, 2006, astro-ph/0602161. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML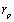 , in AU, its velocity
, in AU, its velocity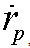 , in km s
, in km s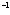 , unmodeled acceleration
, unmodeled acceleration 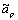 , in
, in 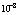 cm s
cm s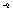 (See plans and figure in[20]) and predicted magnitude of acceleration
(See plans and figure in[20]) and predicted magnitude of acceleration 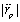 , in
, in 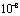 cm s
cm s
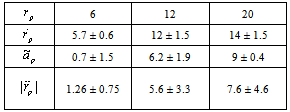
 in AU, eccentricities
in AU, eccentricities 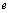 , orbital periods
, orbital periods 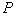 in years, mean squared radial velocities
in years, mean squared radial velocities 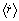 in
in 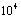 cm s
cm s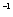 , coordinate
, coordinate 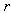 , predicted magnitude of additional radial accelerations
, predicted magnitude of additional radial accelerations 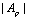 in
in 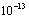 cm s
cm s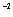 and determined from observations anomalous radial accelerations
and determined from observations anomalous radial accelerations 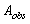 in
in 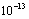 cm s
cm s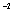 for the planets[21] and asteroid Icarus[34]
for the planets[21] and asteroid Icarus[34]