-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
2012; 2(4): 76-85
doi: 10.5923/j.fs.20120204.04
Conductometric Study of Complex Formation Between Cu (II) Ion and 2-hydroxyimino-3-(2'-hydazonopyridyl)-butane (HL)
E A. Gomaa , K. M. Ibrahim , N. M. Hassan
Chemistry Department, Faculty of Science, Mansoura University, 35516 , Mansoura, Egypt
Correspondence to: E A. Gomaa , Chemistry Department, Faculty of Science, Mansoura University, 35516 , Mansoura, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The association constant ,formation constants and Gibbs free energies are calculated from the conductometric titration curves of CuCl2 with 2-hydroxyimino-3-(2’-hydazonopyridyl)-butane (HL) in absolute ethanol at different temperatures( 293.15 K , 298.15 K , 303.15 K and 308.15 k). On drawing the relation between molar conductance and the ratio of metal to ligand concentrations, different lines are obtained indicating the formation of 1:2 , 1:1 and 2:1 (M:L) stoichiometric complexes. The formation constants of different complexes in absolute ethanol follow the order: Kf (2:1) > Kf (1:1) > Kf (1:2) for (M: L). As the temperature increases, the formation constants and association constants of different complexes increase. The enthalpy and entropy of formation and association of CuCl2 with HL were also estimated and their values were also discussed. The solvation free energies (∆Gs) ,Enthalpy changes of solvation (∆Hs)and the entropy of salvation (∆Ss) were also calculated from solubility measurements for 2-hydroxyimino-3-(2- hydrazonopyridyl)-butane (HL) at different temperatures (293.15 K,298.15 K,303.15 K and 308.15 K).
Keywords: Association Constants, Formation, Gibbs Free Energies, Solvation Free Energies, Enthalpy Changes of Solvation
Article Outline
1. Introduction
- Schiff bases hydrazone derivatives and their metalcomplexes have been studied for their interesting and important properties, e.g., antibacterial[1,2], antifungal[3],antioxidant[4], anticancer[5] and catalytic activity in oxidation of cyclohexene[6]. Moreover, Schiff bases hydrazonederivatives are versatile ligands and they offer the possibility of different modes of coordination towards transition metal ions. Also, some of these derivatives have been applied as iron chelate or drugs in therapy of anaemia[7] and treatment of neuropathic pain[8].Therefore it prompted us to study Schiff base transition metal complexes. Transition metal ions have a strong role in bio-inorganic chemistry and redox enzyme systems and may provide the basis of models for active sites of biological systems[9]. Copper (II) ion is a biologically active, essentialon, cleating ability and positive redox potential allow participation in biological transport reactions. Cu(II) complexes possess a wide range of biological activity and are among the most potent antiviral, antitumor and anti inflammatory agents[10]. Schiff base transition metal complexes have been extensively studied because of their potential use as catalysts in a wide range of oxidation reactions[11–14]. In recent years many copper, nickel and manganese complexes of Schiff bases were prepared and characterized by several techniques[15, 16].
2. Objectives
- This work deals with the determination of solvation free energies (∆Gs) ,enthalpy changes of solvation(∆Hs) and the entropy of solvation (∆Ss) from solubility measurement and identification of coordination behaviour of Schiff base ligand HLtowards CuCl2.and the determination of thethermodynamic stability constants and thermodynamic functions using the conductometric technique. Thus, thermodynamic studies of complexation reactions of this Schiff base with transition metal ions not only result in important information on the thermodynamics of complexation reaction, but also lead to a better understanding of the high selectivity of this ligand towards different metal cations. The aim of this work the evaluation the non-covalent behavior of CuCl2 with2-hydroxyimino-3-(2'-hydazonopyridyl)-butane (HL) in absolute ethanol solutions at 294.15 K. These non-covalent interactions can help us for analysis of salts in bodies and environnement[17].
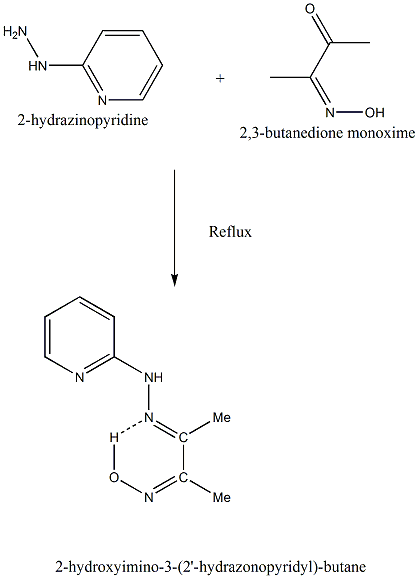 | Scheme. (1). The outline of the synthesis of 2-hydroxyimino-3-(2'-hydrazonopyridyl)-butane (HL) |
3. Methods
3.1. Materials
- All manipulations were performed under aerobic conditions. The cupper chloride and the used reagents were Merck pure.
3.2. Preparation of HL
- 2-hydroxyimino-3-(2'-hydrazonopyridyl)-butane (HL) (scheme 1) was prepared by boiling an EtOH solution of 2-hydrazino pyridine (Aldrich) with 2, 3-butanedione monoxime (1:1) under reflux. The product was recrystallised from hot absolute EtOH[ 18]. (M.p: 220℃; yield 80%). The purity of the compound was checked by TLC.
3.3. Conductometric Measurement
- The conductometric titration of the CuCl2 (1x10-4) mole/L against the ligand (1x10-3) mole/L in absolute ethanol was performed with 0.2 ml interval additions from HL solution. The specific conductance values were recorded using conductivity bridge ADWA, AD 3000 with a cell constant equal to 1 cm -1. The temperature was adjusted at 293.15 K, 298.15 K, 303.15 K and 308.15 K
3.4. Solubility Measurment
- Saturated solutions of HL were prepared by dissolving an excess amount of the solid substances in 10 ml. of the corresponding solvent mixtures, using closed test tubes. The solutions were vigorously shaken in a thermostaticwater-bath at the desired temperature. The molal solubilities of the HL were analysed by drying 1ml. of the saturated solutions in small aluminium dishes. Evaporation of the solvent was performed carefully and slowly under a tungsten lamp to prevent any loss in salt weight. Solubility value was taken as an average of three consecutive independent measurements.
4. Results and Discussion
4.1. Association Constants
- The specific conductance values (Ks) of different concentrations of CuCl2 in absolute ethanol were measured experimentally in absence and in the presence of ligand at different temperatures (293.15 K , 298.15 K , 303.15 K and 308.15 K).The molar conductance (/\m) values were calculated[19] using equation (1):
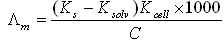 | (1) , |
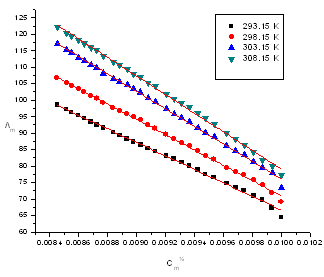
 | Figure (1). The relation between molar conductance (and\m) and (Cm½) of CuCl2 alone in absolute ethanol at different temperatures (293.15K, 298.15 K, 303.15 K and 308.15 K) |
 | Figure (2). The relation between molar conductance (/\m) and (Cm½) of CuCl2 in presence of HL in absolute ethanol at different temperatures (293.15K, 298.15 K, 303.15 K and 308.15 K) |
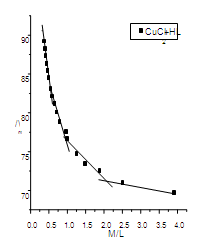 | Figure (3). The relation between /\m and M/L (CuCl2-HL) at 293.15 K |
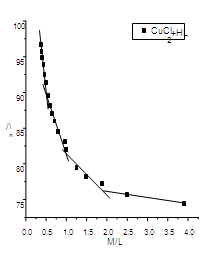 | Figure (4). The relation between/\m and M/L (CuCl2-HL) at 298.15 K |
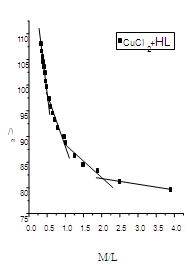 | Figure (5). The relation between /\m and M/L(CuCl2-HL) at 303.15 K |
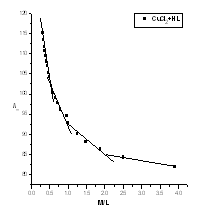 | Figure (6). The relation between /\m and M/L (CuCl2-HL) at 308.15K |
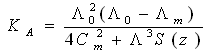 | (2) , |
4.2. Gibbs Free Energies of Association
- The Gibbs free energies of association (ΔGA) were calculated from the association constant[23, 24] by applying equation:
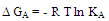 | (3) |
4.3. The Formation Constants for Complexes
- The formation constants (Kf) for CuCl2 complexes were calculated for each type of complexes (1:2), (1:1) and (2:1) (M: L)[25, 26] by using equation:
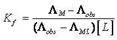 | (4) |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4.4. Gibbs Free Energies of Complex Formation
- The Gibbs free energies of formation for eachstoichiometric complexes were calculated by using the equation:
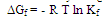 | (5) |
4.5. Enthalpies and Entropies
- The enthalpy (ΔHA) for CuCl2 complexes were calculated for each type of complexes (1:2) , (1:1) and (2:1) (M:L) by using Van't Hoff equation[26,27] :
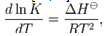 | (6) |
4.6. Enthalpies and Entropies of Association
- From the relation between log K and 1/T, ΔHA can be calculated for each type of complexes from the slope of each line (-ΔH/2.303 R).The entropy (ΔSA) for CuCl2 complexes were calculated for each type of complexes (1:2), (1:1) and (2:1) (M:L) by using equation :
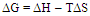 | (7) |
4.7. Enthapies and Entropies of Complex Formation
- The enthalpy (ΔHf) for CuCl2 complexes were calculated for each type of complexes (1:2) , (1:1) and (2:1) (M:L) by using van 't Hoff equation .The calculated values of (ΔHf) and (ΔSf) for CuCl2-ligand stoichiometric complexes are presented in Table (6):
4.8. Acivation Energies
- Since the conductance of an ion depends mainly on its mobility, it is quite reasonable to treat the rate process taking place with the change of temperature on the basis of equation (8) :
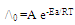 | (8) |
4.9. Soubility Measurement
- The solubility (S) of2-hydroxyimino-3-(2'-hydazonopyrridyl)-butane (HL) in (EtOH-H2O) mixtures at different temperatures (293.15, 298.15, 303.15 and 308.15 K) was determined by gravimetric technique. The results are illustrated in Table 1. Solubility was calculated as an average of the two experimental data. The molal solubility is calculated by using equation (9):Molal solubility (S) = W.1000/do.M g.mole /1000 g .
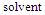 | (9) |
|
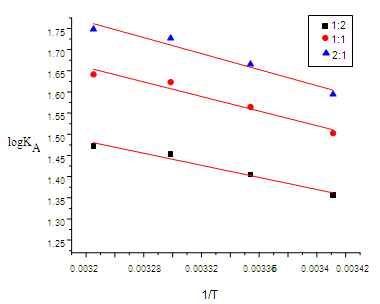 | Figure (7). The relation between (log KA) and (1/T) |
|
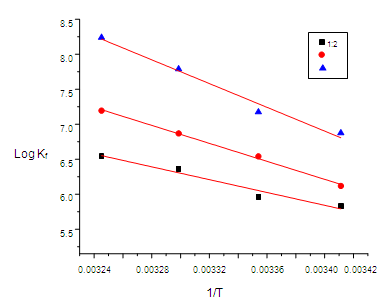 | Figure (8). The relation between (log Kf) and (1/T) |
|
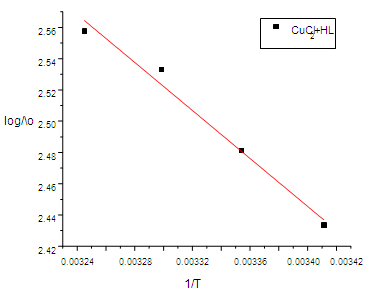 | Figure (9). The relation of (log /\0) and 1/T |
|
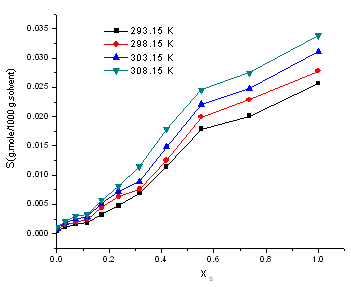 | Figure (10). Variation of the molal solubility (S) of HL with the mole fraction (Xs) of EtOH at different temperatures |
|
4.10. Thermodynamics of Solvation
- The solvation free energies ∆GS of HL in EtOH-H2O mixture at different temperatures(293.15 K,298.15 K, 303.15 K and 308.15 K) were calculated from the solubility measurements by using the following equation (10):
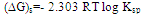 | (10) . |
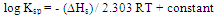 | (11) |
5. Conclusions
- The stability constants for the complexation of copper (II) ion with 2-hydroxyimino-3-(2'-hydazonopyridyl)-butane (HL) were determined conductometrically at different temperatures. Thermodynamic parameters of complexation were determined from the temperature dependence of the formation constant. The negative values of ∆G show the ability of the studied ligand to form stable complexes and the process trend to proceed spontaneously. However, the obtained positive values of ∆H means that enthalpy is not the driving force for the formation of the complexes. Furthermore, the positive values of ∆S indicate that entropy is responsible for the complexing process. The formation constants and Gibbs free energies of different complexes follow that order: Kf (2:1) › Kf (1:1) › Kf (1:2) for (M:L), and ∆Gf (2:1) › ∆Gf (1:1) › ∆Gf (1:2) for (M:L)
References
| [1] | S.M Emam, F.A. El-Saied, S.A. Abou El-Enein, H.A. El-Shater, Spectrochim. Acta Part A 72 (2009) 291–297. |
| [2] | A.R. Yaul, V.V. Dhande, A.S. Aswar, Rev. Roum. Chim. 55 (2010) 537–542. |
| [3] | A.S. El-Tabl, F.A. El-Saied,W. Plass, A.N. Al-Hakim, Spectrochim. Acta Part A 71 (2008) 90–99. |
| [4] | Y. Li, Z.-Y. Yang, M.-F.Wang, J. Fluoresc. 20 (2010) 891–905. |
| [5] | S.B. Desai, P.B. Desai, K.R. Desai, Heterocycl. Commun. 7 (2001) 83–90. |
| [6] | M.S. Niasari, A. Amiri, Appl. Catal. A 290 (2005) 46–53. |
| [7] | M.C.R. Arguelles,M.B. Ferrari, F. Bisceglie, C. Plizzi, G. Pelosi, S. Pinelli,M. Sassi, J. Inorg. Biochem. 98 (2004) 313–321. |
| [8] | P. Yogeeswari, N.Menon, A. Semwal,M. Arjun, D. Sriram, Eur. J.Med. Chem. 46 (2011) 2964–2970 |
| [9] | M.V. Angelusiu, S.F. Barbuceanu, C. Draghici, G.L. Almajan, Eur. J. Med. Chem. 45 (2010) 2055–2062,F. W C Vosburg and G R Cooper, J.Am. Chem. Soc., 1941, 63, 437. |
| [10] | L. Canali, D.C. Sherrington, Chem. Soc. Rev. 28 (1999) 85–93. |
| [11] | G.J. Kim, J.H. Shin, Catal. Lett. 63 (1999) 83–89. |
| [12] | T. Katsuki, Coord. Chem. Rev. 140 (1995) 189–214. |
| [13] | K.J. O’Connor, S.J.Wey, C.J. Burrows, Tetrahedron Lett. 33 (1992) 1001–1004. |
| [14] | M.J. Samide, D.G. Peters, J. Electroanal. Chem. 443 (1998) 95–102. |
| [15] | Losada, I. Del Peso, L. Beyer, Inorg. Chim. Acta 321 (2001) 107–115. |
| [16] | Zhibo Yang, , Ph.D. thesis, Wayne State University, Detroit, Michigan, USA., 2005. |
| [17] | Kamal M.Ibrahim, Magdy M.Bekhit and Gaber M.Abu EL-Reash (1991) Transition Met .Chem, 16,189-192. |
| [18] | W. Gryzybkowski, and R Pastewski,. (1980) Electrochimica Acta 25, 279 |
| [19] | N.A El-Shishtawi, , M.A Hamada,. and E.A. Gomaa, (2010) J. Chem. Eng. Data 55, 5422 |
| [20] | M.A. Hamada, , N.A El-Shishtawi, . and E.A. Gomaa, , (2009), South . Braz . J.Chem. 17, 33 |
| [21] | E.A. Gomaa, (1987) Thermochimica Acta 120, 183 |
| [22] | E.A. Gomaa , (1988) Thermochimica Acta 128, 99 |
| [23] | F.I. El-Doussoki, (2008) Journal of Molecular Liquids 142, 53 |
| [24] | Farid I. El-Doussoki, , Journal of Molecular Liquids, vol.142, pp.53-56, 2008. |
| [25] | M., Rahmi-Nasrabadi, F.Ahmedi, , S.M., Pourmor-tazari, M.R. Ganjal, and K Alizadeh,. (2009) Journal of Molecular Liquids 144, 97 |
| [26] | P.W. Atkins, (1978), Physical Chemistry, Oxford University Press. |
| [27] | C. Burgdorff, T. Kircher, Photo physical properties of tetracene derivatives in solution, Spectrochim. Acta part A, 44, 11 (1988), 1137–1141. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML