-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
2012; 2(4): 53-57
doi: 10.5923/j.fs.20120204.01
Pointing Out the Obstacle of Quantification of Quantum Discord
1Jogesh Chandra Chaudhuri College,Kolkata-700033,West Bengal,India
2Kamaria High Madrasah (School),Kamaria,Joynagar, South 24 paraganas, India
Correspondence to: Amit Bhar , Jogesh Chandra Chaudhuri College,Kolkata-700033,West Bengal,India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Composite quantum systems can be in generic states characterised not only by entanglement but also by more general quantum correlations .The inter-relation between these two quantities ensures of non-locality is still not completely understood. Last few years people are concentrating in studying the different aspects of non-locality of quantum mechanics. Many correlation measures have been introduced and well studied. Quantum discord is one of such correlation measure that creates new challenges among the physicists and mathematicians. New quantification of quantum discord is one of the fascinating area .The analytic formula has been introduced only two qubit X states only. So in this paper we study for the investigation of the difficulties in finding the analytic expression of quantum discord in general two and higher dimension quantum systems.
Keywords: Quantum Entanglement, Quantum Discord, Incomparability, LOCC
Article Outline
1. Introduction
- In the quantum information and computation theory, quantum entanglement, a non-classical correlation, is the key resource and a most remarkable feature. Quantum entanglement was first introduced by Einstein, Podolsky and Rosen (EPR)[1] and also Schrödinger[2]. There was a question in[1] by EPR, whether quantum mechanics is local and complete theory or not? In this context, Bell[3] has given a very significant result : the well known Bell’s Inequality and the consequent features of quantum mechanics are usually called non-local theory. It is accepted that quantum entanglement is responsible for the non-locality of quantum mechanics and the performances of so many information theoretic tasks like Teleportation, Dense coding, Cloning and many others[4-6]. Hence characterization and quantification of quantum entanglement are the most important tasks of quantum information and computation theory.But there exist non-classical correlations other than entanglement for a composite systems. Quantum entanglement is quantifiable. Practical application of it demands quantification. Von-Neumann Entropy, entropy of entanglement for pure state entanglement[7], Entanglement of formation, Distillability[8,9,10,11,12,13,14], and Concurrence[15,16] are the very useful measures of quantum entanglement – a non-classical correlation. Now the most popular measure introduced by Olliver and Zurek[17] and separately by Hendersen and Vedral[18] is quantum discord- which is much better than the other measures and can find out the non-classical correlations even in separable states. Quantum discord brought as an information theoretic measure of the ‘quantumness’ of correlations[19] and is used to determine some results in thermodynamics[20]. Characterizing correlations in terms of its quantum discord, it is proved that classical correlations leads to completely positive reduced dynamics and the induced maps can be completely non-positive when quantum correlations is present[21] and completely positive(CP) maps arise exclusively from the class of separable states with vanishing quantum discord[22]. Use of quantum discord for the characterization of correlations present in the quantum computational model DQC1, introduced by Knill and Laflamme reveals that non-zero values of discord indicates non-classical correlations whenever there is no entanglement between the two parts[23]. A large amount of discord is found but no entanglement in the experiment by the implementation of DQC1 in an all-optical architecture[24]. Also in the DQC1 model, it is proved that a non-zero quantum discord implies a non-zero shift under locally non-effective unitary operations(LNUs)[25]. In the dissipative dynamics of two-qubit quantum discord under Markovian environments, comparison of the dynamics of entanglement with that of quantum discord was made and shown that the entanglement suddenly disappears in all cases where quantum discord vanishes only in the asymptotic limit as the individual decoherence of the qubits, also in finite temperature. Which concludes that quantum discord is more robust than the entanglement against decoherence so that quantum algorithms depending on the correlation ‘quantum discord’ may be more robust than those based on quantum entanglement[26]. Study of quantum discord for two-qubit states gives that for separable states, the entanglement of formation always vanishes but discord does not vanish implies the superiority of quantum discord[27].For finding the monotonic nature of quantum discord ,a few discussion on incomparability and majorization is required. The monotonic nature of quantum discord through incomparability is also observed here.But our present discussion, we are concentrating in the difficulties in the quantification of quantum discord.
2. Concept of Quantum Discord
- Now we know that a bipartite quantum state has both classical and quantum correlations. An information theoretic measure of a bipartite quantum state is ‘quantum mutual information’. I. Quantum mutual information : Let the two parts are A and B and their corresponding Hilbert spaces are
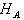 and
and 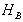 respectively. We consider a density operator
respectively. We consider a density operator 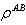 in
in 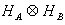 of the composite bipartite system AB, and
of the composite bipartite system AB, and 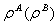 the density operators of part A(B) respectively, then the quantum mutual information is defined as:
the density operators of part A(B) respectively, then the quantum mutual information is defined as: 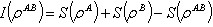 where
where 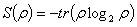 is the von Neumann entropy.Mutual information is the maximum amount of information that A can securely send to B if a composite correlated quantum state is used as the key for a one-time pad cryptographic system[28]. Quantum mutual information is the sum of classical correlation
is the von Neumann entropy.Mutual information is the maximum amount of information that A can securely send to B if a composite correlated quantum state is used as the key for a one-time pad cryptographic system[28]. Quantum mutual information is the sum of classical correlation 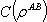 and quantum correlation
and quantum correlation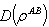 , that is,
, that is, 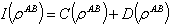 This quantum part
This quantum part 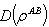 is called quantum discord.II.Quantum discord:Now, the mutual information may be written as
is called quantum discord.II.Quantum discord:Now, the mutual information may be written as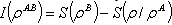 where
where 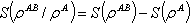 denotes quantum conditional entropy.Let the projection operators
denotes quantum conditional entropy.Let the projection operators 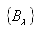 represents a von Neumann measurement for subsystem B only, then the conditional density operator
represents a von Neumann measurement for subsystem B only, then the conditional density operator 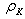 associated with the measurement result K is
associated with the measurement result K is 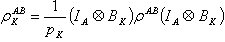 where the probability
where the probability 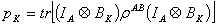 .Then the quantum conditional entropy with respect to this measurement is given by
.Then the quantum conditional entropy with respect to this measurement is given by 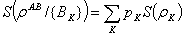 And the associated quantum mutual information of this measurement is defined as
And the associated quantum mutual information of this measurement is defined as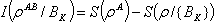 Classical correlation is given by[17,18,27,29]
Classical correlation is given by[17,18,27,29] 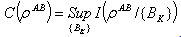 .Calculating
.Calculating 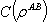 is difficult because it can be obtained by taking maximum over all possible measurement of B. If however, we can find
is difficult because it can be obtained by taking maximum over all possible measurement of B. If however, we can find 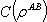 then quantum discord is found by
then quantum discord is found by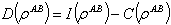 .Review of incomparability under deterministic LOCCEntanglement transformation is a very fundamental problem in quantum information. Here we deal with the question that, if
.Review of incomparability under deterministic LOCCEntanglement transformation is a very fundamental problem in quantum information. Here we deal with the question that, if  be a pure bipartite state then is it possible to transform
be a pure bipartite state then is it possible to transform 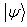 to another state
to another state 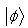 by using LOCC? I.Concept of Majorization: Majorization[4] resolves the question. Let
by using LOCC? I.Concept of Majorization: Majorization[4] resolves the question. Let 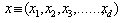 and
and 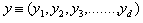 are real d-dimensional vectors. Then x is majorized by y (equivalently y majorizes x), written as
are real d-dimensional vectors. Then x is majorized by y (equivalently y majorizes x), written as 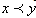 , if for each k in the range 1,2,3,….,d,
, if for each k in the range 1,2,3,….,d,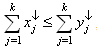 ,Where equality holds for k=d, and where the
,Where equality holds for k=d, and where the 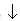 indicates that the components are in decreasing order. Let
indicates that the components are in decreasing order. Let  be the state of the first obtained by taking trace on second party and
be the state of the first obtained by taking trace on second party and 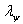 be the vector of eigen values of
be the vector of eigen values of 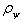 . Then Theorem[5]:
. Then Theorem[5]: 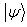 transforms to
transforms to 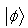 using LOCC if and only if
using LOCC if and only if 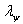 is majorized by
is majorized by 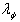 or
or 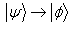 iff
iff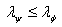 where
where 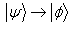 indicates that
indicates that 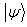 transforms to
transforms to 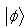 .II. Incomparability: If
.II. Incomparability: If 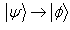 is not possible with probability one under LOCC then we denote this by
is not possible with probability one under LOCC then we denote this by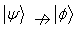 . But it may possible that
. But it may possible that 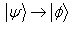 under LOCC with probability one. If for a pair of pure bipartite state (
under LOCC with probability one. If for a pair of pure bipartite state (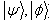 ,
,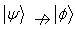 and
and 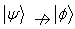 both happens then we call (
both happens then we call (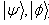 as a pair of incomparable states.In
as a pair of incomparable states.In 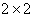 systems, there do not exist incomparable pair of states. But in
systems, there do not exist incomparable pair of states. But in 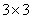 system incomparable pair of states exist. For the criterion of incomparability for a pair of pure entangled states
system incomparable pair of states exist. For the criterion of incomparability for a pair of pure entangled states 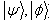 of
of 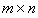 systems where min{m,n}=3, we have the following way. Let
systems where min{m,n}=3, we have the following way. Let 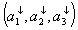 and
and 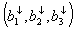 are the Schmidt vectors corresponding to the states
are the Schmidt vectors corresponding to the states 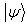 and
and 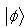 respectively and
respectively and 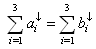 .Then it can be obtained from Nielsen’s criterion that
.Then it can be obtained from Nielsen’s criterion that 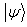 and
and 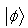 are incomparable if and only if either
are incomparable if and only if either 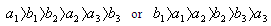 . All the above studies is for the deterministic transformation.
. All the above studies is for the deterministic transformation.3. Analitical Approach in Quantification Procedure of Discord
- It is briefly discussed and completely explained[30] that for two-qubit X-states quantum discord can be found. The method applied for finding quantum discord has required the use of the von-Neuman measurements for the subsystem B as
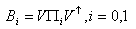 where
where 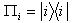 is the projector for the subsystem B for the basis
is the projector for the subsystem B for the basis 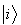 and
and 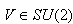 .I.von-Neuman measurements in
.I.von-Neuman measurements in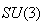 Here we are emphasizing on a bipartite three-qubit system. So here the von-Neuman measurement for the subsystem B is Bi = VПiV†, i =0,1,2.Where
Here we are emphasizing on a bipartite three-qubit system. So here the von-Neuman measurement for the subsystem B is Bi = VПiV†, i =0,1,2.Where 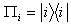 is the projector for the subsystem B for the basis
is the projector for the subsystem B for the basis 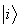 and
and 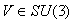 .Any element in
.Any element in 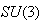 can be expressed as
can be expressed as 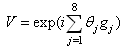 Where
Where 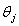 are real numbers and
are real numbers and 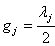 where
where 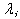 ’s are the Gell-Mann matrices.We see that
’s are the Gell-Mann matrices.We see that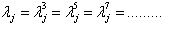 and
and 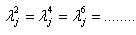 , for
, for 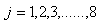 These yields the expression of V in[30] as
These yields the expression of V in[30] as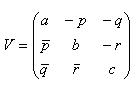 Where
Where 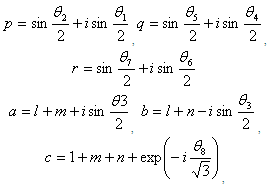 and
and 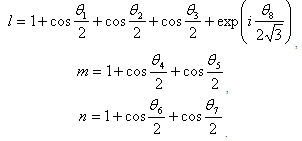 .Then
.Then 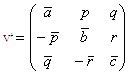 Now von-Neumann measurement for subsystem B areBi= VПiV† , i=0,1,2.Where
Now von-Neumann measurement for subsystem B areBi= VПiV† , i=0,1,2.Where 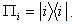 .B0, B1, B2 are expressed as
.B0, B1, B2 are expressed as 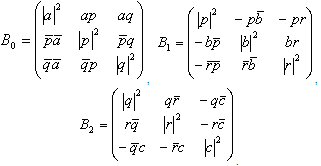 II. Quantification of Discord: Let us consider an example to clarify such concept for bipartite three-qubit system by taking an arbitrary state
II. Quantification of Discord: Let us consider an example to clarify such concept for bipartite three-qubit system by taking an arbitrary state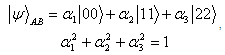 Then
Then and the expression for
and the expression for 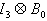 is found as
is found as  So for calculating the ensemble
So for calculating the ensemble 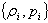 for the state
for the state 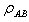 , we know that
, we know that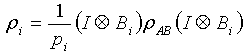 and
and 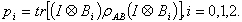 Here we get the
Here we get the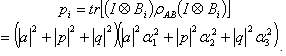 .Hence the eigen values of
.Hence the eigen values of 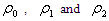 , are 1,0,0,0,0,0,0,0,0.These gives
, are 1,0,0,0,0,0,0,0,0.These gives 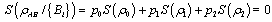 .The classical correlation coefficient becomes
.The classical correlation coefficient becomes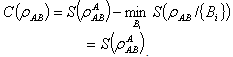 .So the quantum discord
.So the quantum discord 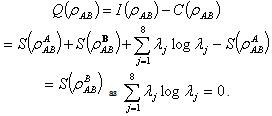 For
For 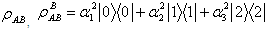 yields
yields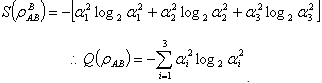 And so for bipartite qudit systems, we have
And so for bipartite qudit systems, we have 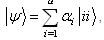 ,we get
,we get 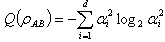 Which is von-Neumann Entropy of the reduced system of
Which is von-Neumann Entropy of the reduced system of 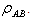 .Monotonicity of Quantum discord under deterministic incomparabilityIn this section our attempt to observe the monotonic nature of quantum discord under deterministic incomparability LOCC. For this consider
.Monotonicity of Quantum discord under deterministic incomparabilityIn this section our attempt to observe the monotonic nature of quantum discord under deterministic incomparability LOCC. For this consider 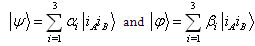 where
where 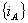 and
and 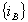 are the orthogonal basis of the respective Hilbert spaces
are the orthogonal basis of the respective Hilbert spaces 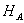 and
and 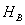 . Now the observations on the analytic expression of quantum discord it is really established the fact Discord
. Now the observations on the analytic expression of quantum discord it is really established the fact Discord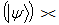 Discord
Discord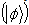 according to the numerical values of
according to the numerical values of 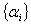 and
and 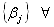 i=1,2,3. So in general we have no such stick monotonic nature of the quantum discord of the two incomparable pairs
i=1,2,3. So in general we have no such stick monotonic nature of the quantum discord of the two incomparable pairs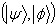 .
.4. Conclusions
- Quantum discord is more powerful feature for realizing the non-locality aspect of quantum mechanics than quantum entanglement because some separable states have non-zero quantum discord. In this paper our aim is to find out the mathematical difficulties in the calculating procedure of Quantum discord. We observe that even in
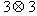 , the large expressions of elements of the matrix are really hard to handle. So it obstacles us for finding the eigen values of the matrices. The next big problem is due to the optimization occurred in the expression of the Quantum discord. So finding the general expression of Quantum discord in this above mathematical process is really a great challenge to the people. Though many tight bounds have been discovered and theoretical works have been done the analytic expression for this discord in higher dimension is not yet found.
, the large expressions of elements of the matrix are really hard to handle. So it obstacles us for finding the eigen values of the matrices. The next big problem is due to the optimization occurred in the expression of the Quantum discord. So finding the general expression of Quantum discord in this above mathematical process is really a great challenge to the people. Though many tight bounds have been discovered and theoretical works have been done the analytic expression for this discord in higher dimension is not yet found. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML