1. Introduction

The classical Maxwell fluid model, known as a viscoelastic rate type model, has been introduced by Maxwell[1] in his investigations on the dynamical theory for gases. The earliest fundaments to this model referred to the manner a body stores energy and produces entropy. Later, a simple mechanical analog[2,4], implemented the standard formulation to the one dimensional (Fig. 1)..

Figure 1. Mechanical analog for the actual model

Rao et al. [5], showed that this model was appropriated for describing polymeric liquids motion. This model considers that both elastic and viscous stress depend on strain. Nevertheless, its use was restricted to dilute polymeric fluids where with relatively short relaxation time. In this paper, and oppositely to the presumptions of Maxwell[1], fluid viscosity and the relaxation time depend on the invariants associated with the stress along with Cauchy-Green stretch tensor or tensors from the appropriate natural configurations. In fact, the thorough study of some polymer melts planar Couette and Poiseuille flows[6], showed that such fluids effective relaxation time depends on the stress and hence may vary in wide ranges.

2. Mathematical Formulation of the Problem

According to the model[7-9], the components of the constituents, namely an energy storing mechanism that is modelled in one dimension as a spring, and the dissipative constituent that is modeled in one dimension as a dashpot, which is assumed to be in series with the spring (Fig. 1). 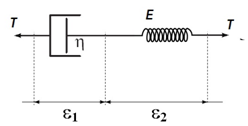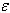The fact that the spring and dashpot are in series leads to the trivial assumptions, hence, in the classical Maxwell one dimensional constitutive model, and in concordance with the notation of Figure 1, the total strain is given by: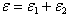

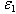(1)

where and 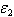are the elongations, in the dashpot and spring respectively.

The stress in the dashpot and spring, respectively 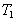and 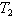, verify the disposition-linked relation: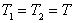

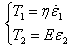
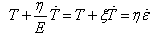
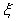(2)

From the constitutive equation for the dashpot and the spring:

(3)

By combining Eq. (1-3), we obtain Maxwell Equation:

(4)

where denotes, in the earliest model, a material constant that has the units of time, or the so-called ‘‘relaxation time”.

Maxwell original model is based on the idea of linear viscoelasticity, which assumes that for small strains, the relaxation modulus is independent of the strain but only depends on the elapsed time. For quantifying this dependence, Macosko[10] defined the relaxation modulus 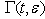as the ratio between the stress and the strain: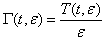

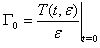
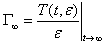
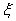(5)

An efficient way to quantify the phenomenon of viscoelasticity consists of evaluating the limit values of the relaxation modulus, the instantaneous elastic modulus:

(6)

and the asymptotic elastic modulus:

(7)

For viscoelastic materials, it has been recorded that stress decreases exponentially[7-9].

3. Results and Discussion

3.1. The Extended Maxwell Fluid Model

According to the results recorded by Larson et al.[6], Gorodtsov et al.[7], M. Graham[8] and Keiller[9] , denotes, in the earliest model, a material constant that has the units of time. In the actual model, the relaxation time is considered as a strain-dependent variable. This configuration has been evoked earlier by Pipkin et al.[11] through the single step strain history model , express by: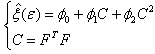

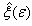(8)

where denotes the relaxation time estimator 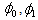and 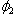are constants, 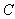is the strain dependent tensorial relaxation function and 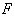is the deformation gradient tensor.

In the actual model, a polynomial scheme is proposed for modeling both relaxation time 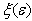and stress 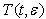in respect to the inherent boundary conditions imposed by Eq. 8.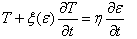

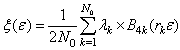
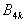3.2. The Boubaker Polynomials Expansion Scheme

The main equation of the model is:

(9)

At this level, The Boubaker Polynomials Expansion Scheme BPES[12-21] is applied through setting the expression:

(10)

where are the 4k-order Boubaker polynomials, 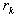are 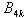minimal positive roots, 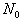is a prefixed integer, 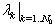are unknown pondering real coefficients. Figure 2 presents relaxation time strain-dependent variations for both actual and single step strain history[11] models.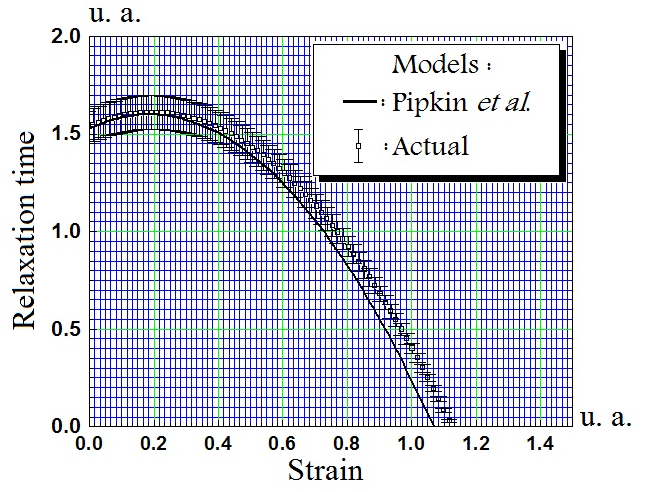

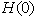Figure 2. Strain-dependent relaxation time for the two related models

The proposed model is tested tough stress responses to a Heaviside step function excitation. Consequently, it comes for Eq. (9) that: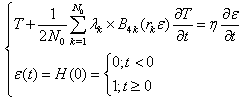

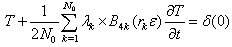
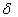(11)

or:

(12)

Where denotes the Dirac delta function.

The BPES protocol ensures the validity of the related boundary conditions expressed through biological conditions, regardless main equation features. In fact, thanks to Boubaker polynomials first derivatives properties: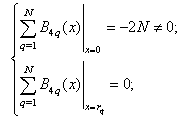

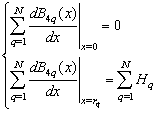
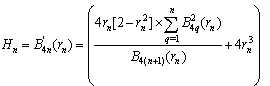(13)

and:

(14)

with:

boundary conditions are inherently verified.

The BPES solution is obtained through four steps:

√ Determining the set of the pondering real coefficients, 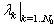which optimize the fitting of Fig. 2.

√ Integrating, for a given value of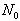, the whole expressions given by Eq. (12) along time domain.

√ Writing the time dependent solution for stress as a sum of solutions to the 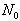elementary k-indexed equations:

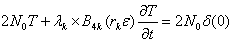√ Incrementing.

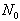√ Testing the convergence of the coefficients .

3.3. Plots and Discussion

Plots of the solution are gathered in Fig. 3.

Figure 3. Model stress response to a Heaviside step excitation for different values of

The obtained profile (Fig. 3) is in good agreement with the exponential responses recorded by Schmidt et al.[22,23], Oldham et al.[24], Padovan[25], Singh et al.[26] and Yuan et al.[37]. In this solution, and oppositely to some recently performed results, there was no free constant at the level of the initial increment, since all conditions have been fulfilled inherently through the application of the Boubaker Polynomials Expansion Scheme BPES[12-21]. Pipkin et al.[11] discussed a similar solution of the same problem for a Maxwell fluid. The free constant has been determined by means of the boundary fluid layer thickness[11] and the related model required some additional initial conditions apart from the requirement i. e. that the fluid was initially at rest or assuming that the time derivative of velocity is zero at time t = 0 as proposed by Rajagopal et al.[28-31]. In such models, the unexpected vanishing of the time derivative of the velocity at t = 0 obviously corresponds to a non-realistic absence of the shear stress. This anomaly has corrected in the actual model through the conditions expressed by Eq. (11-14).

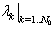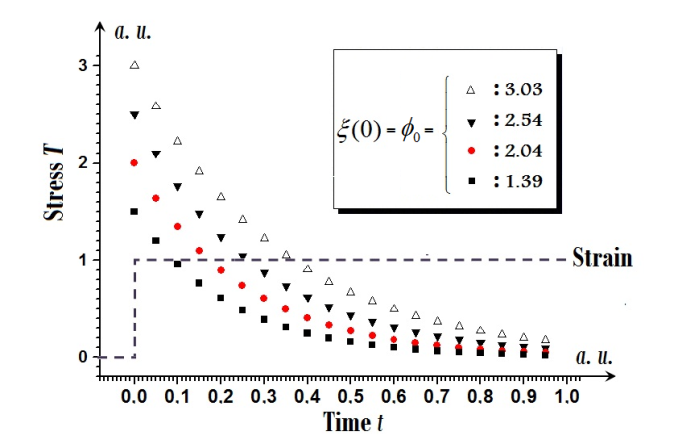
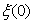
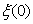An additional ote concerns the fluid behavior with decreasing values of . In fact case when the 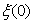decreases, tends to zero, the results for Newtonian fluids[32-37] is recovered.

4. Conclusions

In this study, the exact and approximate expressions for the response of an enhanced a Maxwell fluid model have been established. As a consequence, terms of shear stress response. In the special case when the retardation time decreases, the results for Newtonian fluids have been recovered. In the proposed model, we had to assume that the stresses in the individual constituents and also the body as a whole are the same. We had also assumed the additive decomposition of the strain of the constituents. Such an assumption is questionable if large strains are involved and we need to consider fluid deformation gradients multiplicative decomposition. This is the object of further studies. the changing of the relaxation time with time is outlined in.