-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Frontiers in Science
p-ISSN: 2166-6083 e-ISSN: 2166-6113
2012; 2(3): 24-27
doi: 10.5923/j.fs.20120203.02
The Macroscopic and Microscopic Free Energies of Solvation of Silver Chromate and Silver Phosphate in Some Organic Solvents at 298.15K
Esam A Gomaa
Chemistry Department, Faculty of Science, Mansoura University, Mansoura, Egypt
Correspondence to: Esam A Gomaa, Chemistry Department, Faculty of Science, Mansoura University, Mansoura, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The macroscopic free energies of solvation of silver chromate and silver phosphate in different solvents, acetonitrile (AN), N-methylformamide (NMFA), N-N, dimethylformamide (DMFA), propylene carbonate (PC), dimethyl suphoxide (DMSD), N-methyl-pyrrolidone (NMePy) and ethanol (ETOH) were estimated from the experimental solubility measurements at 298.15K. The macroscopic free energies ∆G(Ma) and free energy of transfer ∆ Gt (Ma) for Ag2CrO4 and Ag3PO4 in the organic solvents represent the macroscopic part of the free energies. The macroscopic free energies for both electrolytes were evaluated experimentally and compared with the microscopic free energies which calculated theoretically. The microscopic free energies of solvation of silver chromate and silver phosphate in the used solvents were theoretically calculated, which are the cavity, the lennard Jones, the induced, the volume and the dipole-dipole free energies and not only electrostatic energy as explained before. The macroscopic and microscopic free energies were compared and discussed.
Keywords: Macroscopic, Microscopic, Cavity, Lennad Jones, Induced, Volume And Dipole-Dipole Energies-Silver Chromate –Silver Phosphate
1. Introduction
- The solubility of an electrolyte is influenced by a wide range of factors, including ion association, variation in ionic activity coefficients, complexation and temperature. Solubility is an equilibrium property enable to thermodynamic parameters through the standard state free energy. Ion pairing can occur in dilute solutions for many electrolytes, particularly these with multivalent ions and for all electrolytes in concentrated solutions. Ion pairing is generally more pronounced in non-aqueous solvents which have lower dielectric constants than water. In effect, the ion pairs represent a reservoir of electrolyte in the solution and increase the solubility.The complexity of the system increases for usymmetrical electrolytes or for mixed electrolyte systems[1].Bjerrum[2] proposed, that the motion of ions would be coupled when the energy of attraction between them exceeded the thermal energy. For solely columbic interactions theory predicts a distance within which the electrostatic attraction between ions is greater than 2kT. Which will be sufficient to couple the motions of the ions .The treatment takes account of only electrostatic interactions and neglects molecularity of solvent.Nevertheless,in low concentration, strong interactions between ions and solvent molecules resulting in ion pair configuration. The three commonly assumed structures are, the first in which the ion retains their individual solvation shells, and so is separated by two solvent molecules. The second in which the ions share some part of their solvation shells so are separated by one molecule and the third where the ions are in contact and share a common solvation shell.The presence of species such creates an experimental difficulty, the different techniques will have different sensitivities to the species present. Thus the conductance will see on the dissociated ions and the presence of ion pairs is determined by difference from experimental molar conductance and that expected for strong electrolyte[3].The formation of complexes (complexation) provides a route to increased solubility. Several equivalent representations of the speciation in these systems have been used[4].Pierotti theory[5] applies the scaled particle theory[6] to estimate solubilities, heats, entropies and molar capacities of solutions.Good agreement between theory and experiment for evaluating the thermodynamic parameters has been obtained for a number of neutral compounds and gases in a variety of solvents[7-11].Many authors like Bjerrum and others reported that the electrostatic energy plays important role in the solvation energy. In this work more work (novel) was done to explain the different types of electrostatic coulombic energy[11].The aim of the present work is to extend the applicability of the scaled particle theory(especially applied for noble gases) as novel method for discussing the solvation of the electrolyte, silver chromate and silver phosphate in different organic solvents. Knowing the other factors affecting the solubility is very important here. Is the electrostatic energy play important role in the solubility or not.
2. Experimental
- Ag2CrO4 and Ag3PO4 are of the type Riedel-de-Häen AG, Seelze- Hannover was used. acetonitrile (AN), N-N, dimethylformamide (DMFA), dimethylsulphoxide (DMSO) and ethanol (EtOH) were obtained from BDH. N- methylformamide (NMFA), propylene carbonate (PC) and N- methyle-pyrrolidone (NMePy) were obtained from Merck (zur analyse). The solubilities of Ag2CrO4 and Ag3PO4 in the organic solvents under consideration were done gravimetrically with at least three measurments as explained in previous works[12-14].
3. Results and Discussion
- The measured molar solubilities for Ag2CrO4 and Ag3PO4 in the organic solvents, AN, NMFA, DMFA, PC , DMSO, NMePY and EtOH as explained in Ref. (8) are listed in Tables (1 and 2). Prediction of electrolyte activity coefficients is one of the classical problems in physical chemistry and is outlined in classical work[13]. The defining characteristic of ions is that they carry a net charge and so the principle interaction between ions are largest contribution to the activity coefficients are coulombic. Debye and Hückel solved the problem for system purely electrostatic interactions between point charges surrounded by a dielectric contnium .Therefore the extended Debye-Huckel equation was applied taking account of the ion size[14]From the activity coefficients ɣ± , calculated using Debye Hückel equation and from the molar solubility data. Values of pKsp Ag2CrO4 were estimated by use of equation (1).
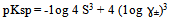 | (1) |
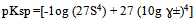 | (2) |
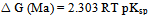 | (3) |
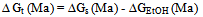 | (4) |
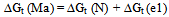 | (5) |
|
|
|
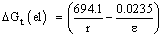 | (6) |
 is solvent dielectric constant[13]. The calculated values of ∆ Gt (N) and ∆Gt (el) for Ag2CrO4 and Ag3PO4 in the organic solvents are also given in Table s(2). It was shown from Table (2) that all the three types of free energies, ∆Gt (Ma), ∆Gt (el) and ∆Gt (N) for Ag2CrO4 and Ag3PO4 have the following order:AN > PC > DMSO > NMFA > NMePy > DMFAFor the calculation of the microscopic free energies for Ag2CrO4 and Ag3PO4 in the organic solvents under consideration at 298.15K, the Pierotti theory[5-7] was applies.This model explains the solvation process through the creation of solute in the solvent followed by interaction. Therefore two difference types of free energies are present, cavity and interaction energy.
is solvent dielectric constant[13]. The calculated values of ∆ Gt (N) and ∆Gt (el) for Ag2CrO4 and Ag3PO4 in the organic solvents are also given in Table s(2). It was shown from Table (2) that all the three types of free energies, ∆Gt (Ma), ∆Gt (el) and ∆Gt (N) for Ag2CrO4 and Ag3PO4 have the following order:AN > PC > DMSO > NMFA > NMePy > DMFAFor the calculation of the microscopic free energies for Ag2CrO4 and Ag3PO4 in the organic solvents under consideration at 298.15K, the Pierotti theory[5-7] was applies.This model explains the solvation process through the creation of solute in the solvent followed by interaction. Therefore two difference types of free energies are present, cavity and interaction energy.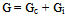 | (7) |
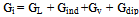 | (8) |
|
|
References
| [1] | Apelblat, Alexander, “Dissociation constants and limiting conductances of organic acids in water”. J.Molecular Liquids, 95(2002)99-145. |
| [2] | Barthel,J ,Wachter,R. and Gores,H.-J., inModern Aspects of Electrochemistry,Coway ,B.E., and Bockris, J.O`M, Editors, Vol.13, pp.1-179. Plenum , 1979. |
| [3] | Barthel, J.M.G., Krienke, H. and Kunz, W.,”Physical Chemistry of Electrolyte Solutions, Modern Aspects”., Springer, , 1998. |
| [4] | Bockris,J.O`M . and Reddy,A.K.N.,”Modern Electrochemistry”,Plenum Press,,1970. |
| [5] | Pierotti, R.A. "Aqueous solutions of nonpolar Gases", J. Phys. Chem.., 69(1965), 281-288 |
| [6] | Reiss, H., Frisch, H.L and Lebowitz, J.L., "Scaled Particle Theory". J. Chem. Phys., 31 (1959) 361 – 388. |
| [7] | Lucas, M. and Feilloly, A. "Prevision de L'enthalpie de dissolution de molécules non polaries dans les mélanges eau-ethanol." Bull. Soc. Chim. , 4 (1970), 1267-1270. |
| [8] | Kim, J.I. and Brückl, "On the temperature dependence of solubilities of inert Gases from the scaled pauticle theory." Z. Phys. Chem. Neue Folge, 110 (1978), 197-208. |
| [9] | Brückl, N. and Kim, J.I., "Gibbs free energies of solute-solvent interactions for He, Ne, Kr, Xe, H2, O2, N2, CH4, SF6, C2H4, CO2 and C2H2 in various solvents; comparison if theoretical prediction with Experiment," Z. Phys. Chem. Neue Folge, 126 (1981), 133-150. |
| [10] | Gunnerson, F.S. and Cronenberg, A.W., "A Prediction of the inert Gas solubilities in Stoichometric molten UO2". J. Nucl. Materials, 58 (1971), 311-230. |
| [11] | Treiner, C., "Use of the scaled particle theory for the determination of single Ion standard free energy of transfer between solvents". Cand.J.Chem. 55(1977) 682-685. |
| [12] | Gomaa, E.A., "Solubility of tetraphenyl derivatives Ph4C, Ph4Ge and Ph4AsBPh4 in aqueous hexamethyl phosphortriamide solutions at 25℃, Ind. J. of Tech., 24(1986), 725-726. |
| [13] | Gomaa, E,A., "Theoretical contribution of solvation of AgBr in some organic solvents at 25℃". Thermochimica Acta, 128 (1988) 99-104. |
| [14] | Gomaa, E.A., "Application of the scaled particle theory for the solvation of silver tetraphenyl-boride in dimethyl formamide water mixtures at 298.15K, J. King Saud Univ., 3 (1991), 69- 76. |
| [15] | Ionic Radius from Wikipedia, the free encyclopedia. |
| [16] | Kim, J.I., " The Ph4AsBPh4 assumption of ion solvent interactions and its asymmetric partition to cation and anion". Bull. Soc. Chim. Belg., 95 (1986), 435-446. |
| [17] | Gomaa, E.A. and B.M.Al-Jahdali”, Association of Cu(NO3)2 eith Kryptofix-221 in mixed (MeOH-DMF) solvents at different temperatures.”, American Journal of Fluid Dynamics, 1(1),2011,4-8. |
| [18] | Nagah A.El-Shishtawi,Maany a.Hammada and Esam A. Gomaa,” Inflence of peranent magnet on the association constants of FeCl3 + 10% PVA(polyvinyl alcohol)in 50% ethanol-water solutions conductometrically at 298.15K using new equation for 1:3 asymmetric electrolytes.”, Physical Chemistry, 1(1) ,2011, 14-16. |
| [19] | Gomaa, E.A.,”Solvation parameters of lead acetate in mixed, N,N-dimethylformamide–water mixtures at 298.15K.”, Analele Universitate din Bucuresti-Chimie, vol.19, (2010) 45-48. |
| [20] | Gomaa, E.A. and Al-Jahdalli, B.M., “Conductometric studies of ionic association of divaleny asymmetric electrolyte Cu(NO3)2 with Kryptofix-22 in mixed (MeOH-DMF) solvents at different temperatures”., American Journal of Condensed Matter Physics, 2(2012)16-21. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML