| [1] | X.-Q. Zhao, L. Wang, W. Sun. (2006) The repeated homogeneous balance method and its applications to nonlinear partial differential equations, Chaos, Solitons and Fractals, 28(2), 448-453 |
| [2] | S.J. Liao. (2005) A new branch of solutions of boundary-layer flows over an impermeable stretched plate, Int. J. Heat Mass Transfer, 48, 2529-2539 |
| [3] | S.J. Liao. (2009) A general approach to get series solution of non-similarity boundary-layer flows, Commun. Nonlinear Sci. Numer. Simul., 14(5), 2144-2159 |
| [4] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2010) Exact three-wave solutions for high nonlinear form of Benjamin-Bona-Mahony-Burgers equations, International Journal of Mathematical and Computer Sciences, 6(3), 127-131 |
| [5] | M.T. Darvishi, Mohammad Najafi. (2012) Some exact solutions of the (2+1)-dimensional breaking soliton equation using the three-wave method, World Academy of Science, Engineering and Technology, 87, 31-34 |
| [6] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2010) New exact solutions for the (3+1)-dimensional breaking soliton equation, International Journal of Information and Mathematical Sciences, 6(2), 134-137 |
| [7] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2010) New application of EHTA for the generalized (2+1) -dimensional nonlinear evolution equations, International Journal of Mathematical and Computer Sciences, 6(3), 132-138 |
| [8] | M.T. Darvishi, Mohammad Najafi. (2011) A modification of extended homoclinic test approach to solve the (3+1)- dimensional potential-YTSF equation, Chin. Phys. Lett., 28(4), art. no. 040202 |
| [9] | M.T. Darvishi, Mohammad Najafi. (2012) Some complexiton type solutions of the (3+1)-dimensional Jimbo-Miwa equation, World Academy of Science, Engineering and Technology, 87, 42-44 |
| [10] | M.L. Wang., X.Z. Li, J.L. Zhang. (2008) The -expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics,, Physics Letters A, 372 , 417-423 |
| [11] | M.T. Darvishi, Maliheh Najafi, Mohammad Najafi. (2012) Traveling wave solutions for the (3+1)-dimensional breaking soliton equation by -expansion method and modified -expansion method, World Academy of Science, Engineering and Technology, 88, 37-42 |
| [12] | J.H. He, M.A. Abdou. (2007) New periodic solutions for nonlinear evolution equations using Exp-function method, Chaos, Solitons and Fractals, 34, 1421-1429 |
| [13] | B.C. Shin, M.T. Darvishi, A. Barati (2009) Some exact and new solutions of the Nizhnik-Novikov-Vesselov equation using the Exp-function method, Comput. Math. Appl., 58(11/12) (2009) 2147-2151 |
| [14] | X.H. Wu, J.H. He. (2008) Exp-function method and its application to nonlinear equations, Chaos, Solitons and Fractals, 38(3), 903-910 |
| [15] | R.K. Prud’homme, S.A. Khan (Eds.), Foams: Theory, Measurements and Applications, Dekker, New York, 1996 |
| [16] | D.L. Weaire, S. Hutzler, The Physics of Foams, Oxford University Press, Oxford, 2000 |
| [17] | H.A. Stone, S.A. Koehler, S. Hilgenfeldt, M. Durand. (2003) J. Phys. Condens. Matter., 15, S283-S290 |
| [18] | S. Hilgenfeldt, S.A. Koehler, H.A. Stone. (2001) Dynamics of coarsening foams: Accelerated and self-limiting drainage, Phys. Rev. Lett., 20, 4704-4707 |
| [19] | J.I.B. Wilson. (2003) Essay review, scholarly froth and engineering skeletons, Contemp. Phys., 44, 153-155 |
| [20] | L.J. Gibson, M.F. Ashby, Cellular Solids: Structure & Properties, Cambridge University Press, Cambridge, 1997 |
| [21] | J. Banhart, W. Brinkers. (1999) Fatigue behavior of aluminum foams, J. Mater. Sci. Lett., 18, 617-619 |
| [22] | M.F. Ashby, A.G. Evans, N.A. Fleck, L.J. Gibson, J.W. Hutchinson, H.N.G. Wadley, Metal Foams: A Design Guide, Society of Automotive Engineers, Boston, 2000 |
| [23] | M. Duranda, D. Langevin. (2002) Physicochemical approach to the theory of foam drainage, Europhys. J. E, 7, 35-44 |
| [24] | G. Verbist, D. Weaire. (1994) Soluble model for foam drainage, Europhys. Lett., 26, 631-634 |
| [25] | G. Verbist, D. Weaire, A.M. Kraynik. (1996) The foam drainage equation, J. Phys. Condens. Matter, 8, 3715-3731 |
| [26] | D. Weah, S. Hutzler, N. Pittet, D. Pard. (1993) Steady-state drainage of an equeous foam, Phys. Rev. Lett., 71, 2670-2673 |
| [27] | M.A. Helal, M.S. Mehanna. (2007) The tanh method and Adomian decomposition method for solving the foam drainage equation, Appl. Math. Comput., 190 (1), 599-609 |
| [28] | F. Khani, S. Hamedi-Nezhad, M.T. Darvishi, S.-W. Ryu (2009) New solitary wave and periodic solutions of the foam drainage equation using the Exp-function method, Nonlin. Anal.: Real World Appl., 10, 1904-1911 |
| [29] | P.L.J. Zitha, F.J. Vermolen. (2006) Self-similar solutions for the foam drainage equation, Transp. Porous Media, 63, 195-200 |
| [30] | M.T. Darvishi, F. Khani. (2009) A series solution of the foam drainage equation, Comput. Math. Appl., 58, 360-368 |
| [31] | J.H. He, Variational approach to foam drainage equation, Meccanica, (in press), DOI: 10.1007/s11012-010-9382-0 |
| [32] | J. Wang. (2010) Construction of new exact traveling wave solutions to (2+1)- dimensional mVN equation, Inter. J. Nonl. Sci., 9(3) , 325-329 |

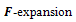 method, we present some explicit formulas of exact traveling wave solutions for the foam drainage equation. A modified
method, we present some explicit formulas of exact traveling wave solutions for the foam drainage equation. A modified 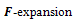 method is proposed by taking full advantages of -expansion method and Riccati equation in seeking exact solutions of non-linear partial differential equations.
method is proposed by taking full advantages of -expansion method and Riccati equation in seeking exact solutions of non-linear partial differential equations.
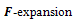 Method
Method
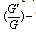 expansion method[10, 11] and the exp-function method[12, 13, 14]. In this paper, we consider the following foam drainage equation
expansion method[10, 11] and the exp-function method[12, 13, 14]. In this paper, we consider the following foam drainage equation 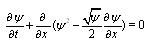
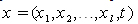 and dependent variable as
and dependent variable as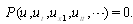
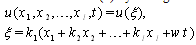
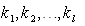 and
and 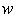 are constants to be determined. Inserting (3) into (2) yields an ODE for
are constants to be determined. Inserting (3) into (2) yields an ODE for 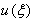
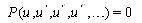
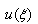 can be expressed as
can be expressed as 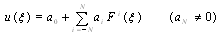
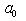 and
and 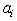 s are constants to be determined.
s are constants to be determined. 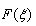 satisfies Riccati equation
satisfies Riccati equation 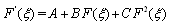
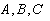 are constants to be determined. Integer
are constants to be determined. Integer 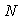 can be determined by considering the homogeneous balance between the governing nonlinear term(s) and highest order derivatives of
can be determined by considering the homogeneous balance between the governing nonlinear term(s) and highest order derivatives of 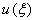 in (4). Substituting (5) into (4), and using (6), then the left-hand side of (4) can be converted into a finite series in
in (4). Substituting (5) into (4), and using (6), then the left-hand side of (4) can be converted into a finite series in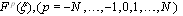 . Equating each coefficient of
. Equating each coefficient of 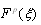 to zero yields a system of algebraic equations for
to zero yields a system of algebraic equations for 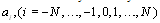 and
and 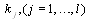 and
and 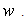 . Then solving the system of algebraic equations, probably with the aid of Maple,
. Then solving the system of algebraic equations, probably with the aid of Maple, 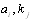 and
and 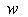 can be expressed by
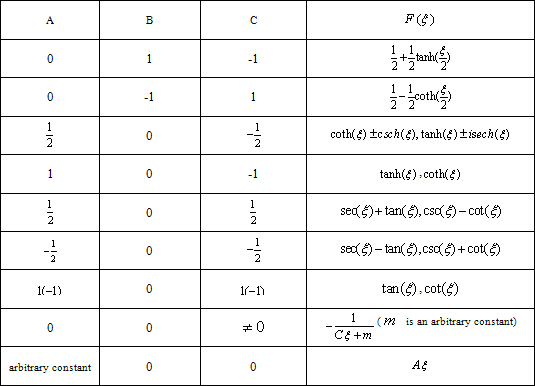
can be expressed by 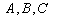 (or the coefficients of ODE (4)). Upon substituting these results into (5), we can obtain the general form of traveling wave solutions to (4). From the general form of traveling wave solutions of equation (6) listed in Table 1, we can give a series of soliton-like solutions, trigonometric function solutions, and exponential function solutions to (2).
(or the coefficients of ODE (4)). Upon substituting these results into (5), we can obtain the general form of traveling wave solutions to (4). From the general form of traveling wave solutions of equation (6) listed in Table 1, we can give a series of soliton-like solutions, trigonometric function solutions, and exponential function solutions to (2).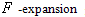 method to construct the traveling wave solutions for foam drainage equation
method to construct the traveling wave solutions for foam drainage equation 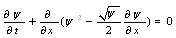
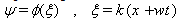
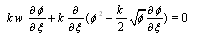
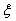 and considering the zero constants for integration we have
and considering the zero constants for integration we have 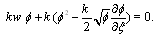
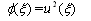
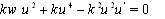
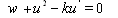
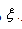 . By balancing the orders of
. By balancing the orders of 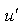 and
and 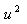 in eq. (13), we have
in eq. (13), we have 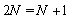 then
then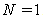 . So we can write
. So we can write 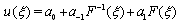
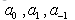 are constants to be determined later. Substituting (14) into (13), and using (6), the left-hand side of (13) can be converted into a finite series in
are constants to be determined later. Substituting (14) into (13), and using (6), the left-hand side of (13) can be converted into a finite series in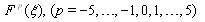 . Equating each coefficient of
. Equating each coefficient of 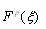 to zero yields a system of algebraic equations for
to zero yields a system of algebraic equations for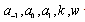 .
. 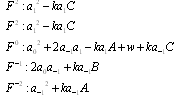
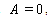 , we have Case 2: when
, we have Case 2: when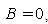 , we have Case 3: when
, we have Case 3: when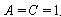 , we have So we can list the solutions of
, we have So we can list the solutions of 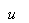 as follows: (1) When
as follows: (1) When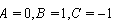 , from Table 1 and Case 1, we have setting
, from Table 1 and Case 1, we have setting 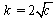 yields the same solution (20) of[28] which is also in agreement with the selection for the solutions in [27, 29]. (2) When
yields the same solution (20) of[28] which is also in agreement with the selection for the solutions in [27, 29]. (2) When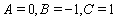 , from Table 1 and Case 1, we haveFor
, from Table 1 and Case 1, we haveFor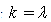 , solution (19) of [28] will obtain.(3) When
, solution (19) of [28] will obtain.(3) When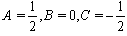 , from Table 1 and Case 2, we have
, from Table 1 and Case 2, we have 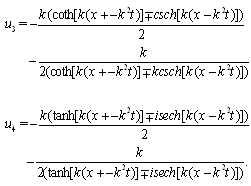
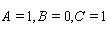 , from Table 1 and Case 2, we have (5) When
, from Table 1 and Case 2, we have (5) When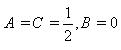 , from Table 1 and Case 3, we have(6) When
, from Table 1 and Case 3, we have(6) When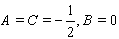 , from Table 1 and Case 2, we have (7) When
, from Table 1 and Case 2, we have (7) When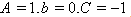 , from Table 1 and Case 2, we have
, from Table 1 and Case 2, we have  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML