-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Food Science and Nutrition Engineering
p-ISSN: 2166-5168 e-ISSN: 2166-5192
2011; 1(1): 8-10
doi: 10.5923/j.food.20110101.03
Application of Nonlinear Programming for Optimization of Nutrient Requirements for Maximum Weight Gain in Buffaloes
Pratiksha Saxena
School of Applied Sciences, Gautam Buddha University, Greater Noida, 201308, India
Correspondence to: Pratiksha Saxena , School of Applied Sciences, Gautam Buddha University, Greater Noida, 201308, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper, nonlinear effects of nutrient ingredients are introduced as an approach closer to the true effects of nutrient ingredients. A nonlinear model is developed to take consideration of nutrient ingredients more effectively. The nonlinear model is introduced in order to maximize the weight gain in buffalo by the optimal use of feed ingredients. Data from a variable caloric density study for buffalo is fitted to nonlinear objective function expression for weight gain of the animal in terms of feed ingredients. National Research Council requirements are introduced as constraints for mathematical model. Proposed model with nonlinear programming measures its performance and gives a comparative result with linear programming models. Thus the study is an attempt to develop a nonlinear programming model for optimal planning and best use of nutrient ingredients.
Keywords: Nonlinear Programming, Nutrient Ingredients, Weight Gain, Feed Formulation, Feeding Standards
Cite this paper: Pratiksha Saxena , "Application of Nonlinear Programming for Optimization of Nutrient Requirements for Maximum Weight Gain in Buffaloes", International Journal of Food Science and Nutrition Engineering, Vol. 1 No. 1, 2011, pp. 8-10. doi: 10.5923/j.food.20110101.03.
Article Outline
1. Introduction
- Since 1940, the year of introduction of the concept of linear programming, fundamentals and applications of linear programming have been explored in great detail. In linear programming, all functional forms dealt with are linear in nature. While formulating a mathematical model related to real life problems, many different situations lead to nonlinear formulation of constraints and objective function. The importance of Nonlinear Programming Applications is growing due to rapidly increasing sophistication of managers and operation researchers in implementing decision oriented mathematical models, as well as to the growing availability of computer routines capable of solving large-scale nonlinear problems. Animal diet formulation techniques are in use for more than hundred years. Objective of animal diet formulation is to provide necessary energy at different stages of produc- tion as growth, reproduction, metabolism and lactation. Basic knowledge of animal nutrition, feed ingredient nutrition information, feed composition and diet formulation techniques are used to formulate the animal diet. Mathemat- ical programming techniques are used to formulate the diet as linear programming, goal programming, multiple- objective programming, separable programming and nonlinearprogramming. Linear programming method is most widely used for this purpose. A linear model is developed (C. Van de Panne et al, 1963) to formulate optimise composition of cattle feed. Incorporation of information on animal performance into the linear programming derivation of optimum livestock rations is taken into consideration (Robert Townsley, 1968). Another model was developed using linear approximation of chance constrained programming (David L. Olson et al, 1987). A quadratic programming model is proposed (Bill R. Miller et al, 1986) and is compared to linear programming model. Focus is shifted to the application of nonlinear programming to the field of animal nutrition (Roush et al., 2007). Comparison between problem types, problem solving approaches and application was reported (Weintraub and Romero, 2006). A mixed-integer nonlinear programming technique is developed for the synthesis of model (Grossmann, 1990). Some of these models represent efficiency of converting any one of the nutrient ingredients to weight gain, while other represent a comparative study of effect of different nutrient ingredient on the weight gain of the animal. Thus, the data available depict the linear relationship between the weight gain and the nutrient ingredients individually, but complexity of different nutrient ingredients would possibly be better described by nonlinear relationship between them.Introduction of nonlinear programming to optimize yield and minimize feed cost in buffalo feed formulation may lead to better approximation as compared to those of linear cases. Present study is carried out to extend the work by inclusion of this nonlinear relation. Leading to the same guideline a ration can be formulated using all its nutrient ingredients simultaneously at the optimum level. In this paper, it is envisaged to develop a mathematical model using non-linear programming to take simultaneous effects of all nutrient ingredients and the diet is optimized by using Kuhn- Tucker conditions. This result is also compared to than that of linear programming formulation of the model.
2. Material and Methods
- The present study is based on the secondary data of animal experiment of Elangovan (1990). Briefly, the study consists of male buffalo calves of about 6-9 months of age, which were procured locally at Bareilly. Animals were dewormed and vaccinated against common contagious diseases. The animals were kept in a shed having cemented floor with individual feeding arrangement during the feeding trial but transferred to metabolic cages during metabolism trial. Drinking water was provided to all calves ad libitum. Three different feed treatments used in the experiment are given to animal which are shown in Table 1.
| |||||||||||||||||||||||||||
3. Result and Discussion
3.1. Weightage of Variables
- First of all, linear relationship for dependent and independent variables is formulated to decide the weightage of the variables. Assuming a linear relationship between weight gain of buffaloes and intake of DM, CP and TDN, the weightage of these variables was decided. Using least square method, the relationship is depicted in the following equation which describes the weightage of the variables x1, x2 and x3.
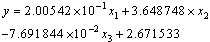 | (1) |
3.2. Relationship between Variables
- By using least square method, the relations between y and x1, y and x2, y and x3 of different degrees were established and then by using F-test the relation of best fit was decided. Applying the F-test, the following most appropriate relationship between the variables were derived:
 | (2) |
3.3. Formulation of Objective Function
- The objective function was established by using the appropriate relations of the variables x1, x2, x3 according to their weightage on weight gain of the buffalo calves. The weightage with respect to total effect of this weightage was considered:
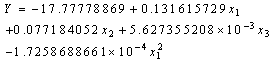 | (3) |
3.4. Constraints
- The constraints according to feeding standards on the above-mentioned variables according to feeding standards of NRC (1981) were applied
 | (4) |
3.5. Problem Defined
- The main problem is formulated to maximise weight gain of the animal:
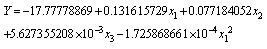 subject to:
subject to: 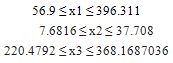 | (5) |
3.6. Solution of the Problem
- Introducing Kuhn-Tucker conditions, the weight gain of the buffalo calves could be maximized as:
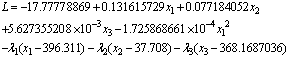 Using Kuhn-Tucker conditions, the following set of equations were obtained for optimal solutions:1.
Using Kuhn-Tucker conditions, the following set of equations were obtained for optimal solutions:1. 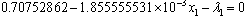 2.
2. 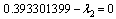 3.
3. 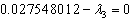 4.
4. 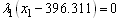 5.
5. 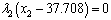 6.
6. 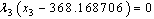 7. x1 ≤ 396.3118. x2 ≤ 37.7089. x3 ≤ 368.168703610.
7. x1 ≤ 396.3118. x2 ≤ 37.7089. x3 ≤ 368.168703610. 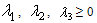 Solving these equations the optimum values of the three nutrients is found out to maximize the body weight gain. Accordingly we have:x1 = 381.3028, x2 = 7.708, x3 = 368.1687036 g/kg W0.75It also gives, λ1 = 0.393301399, λ2 = 0.027548012 which satisfied all the conditions.The problem is also formulized and solved by simplex method and it gives, x1 = 396.311, x2 = 37.708, x3 = 368.1687036 g/kg W0.75Comparison shows that by linear programming result is obtained at corner points of feasible area and optimization is at comparatively at higher values of nutrient ingredients. This comparison represents that non-linear programming is better way to take simultaneous effect of all nutrient ingredients together and maximize the weight gain in animal with optimized value of nutrient ingredients.
Solving these equations the optimum values of the three nutrients is found out to maximize the body weight gain. Accordingly we have:x1 = 381.3028, x2 = 7.708, x3 = 368.1687036 g/kg W0.75It also gives, λ1 = 0.393301399, λ2 = 0.027548012 which satisfied all the conditions.The problem is also formulized and solved by simplex method and it gives, x1 = 396.311, x2 = 37.708, x3 = 368.1687036 g/kg W0.75Comparison shows that by linear programming result is obtained at corner points of feasible area and optimization is at comparatively at higher values of nutrient ingredients. This comparison represents that non-linear programming is better way to take simultaneous effect of all nutrient ingredients together and maximize the weight gain in animal with optimized value of nutrient ingredients.4. Conclusions
- Comparison of the present nonlinear method with linear programming represents that nonlinear programming gives maximum weight gain with optimum use of nutrients. The effect of these nutrients on body weight gain was considered and individual relations as obtained in equations present the linear and nonlinear effects of different ingredient on body weight gain.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML