1. Introduction

Global energy generation, distribution and consumption patterns are rapidly evolving with growth in human population. The focus is quickly shifting towards renewables as a means of unlocking economic development. The interest in renewable energy (RE) sources is derived from the fact that they are sustainable and environmentally benign when compared to conventional energy sources. Between the years 2000 and 2017, renewables were the fastest-growing energy sources, contributing up to 40% to all primary energy increases [1]. Solar PV and wind energy systems recorded the highest deployment rate during this period. The primary impact of solar PV and wind energy systems lies in making production and consumption of energy accessible and inclusive. In locations where grid expansion is prohibitively expensive, off-grid RE systems could be an economically viable substitute. From IRENA report [2], the total global installed capacity of RE systems has leapt from less than 2 GW in 2008 to about 6.5 GW in 2017. In 2016 alone, it was estimated that worldwide, over 122 million people benefited from electricity from off-grid schemes for lighting and other electrical energy related services [2,3]. Asia has proven to be the hub of off-grid renewable capacity expansion as by 2016, 76 million people were electrified using solar lights and solar home systems [2].

There has also been a rapid recognition of off-grid RE systems in Africa. From 2011 to 2016, the number of people accessing electricity from off-grid sources rose from 2 to 58 million and solar lights, solar mini-grids and solar home systems have been the major drivers of this transition [3]. From 2008 to 2017, electricity generation using off-grid means jumped from 231 MW to 1.2 GW and 820 MW was derived from solar lights, solar mini-grids and solar home systems [3]. Although there has been a noticeable increase in generation from hydropower mini-grids from 124 MW to 126 MW in this period, the contribution from off-grid capacity has fallen sharply from 53% to 15% [2]. While the outlook for Kenya, Tanzania, Ethiopia, Nigeria and North African countries heralds huge electrification successes, most of the Sub-Saharan Africa countries to the contrary continue to face acute electricity shortages. As of 2017, 61% of people living in this region’s rural communities did not have access to electricity [3].

A unique case is for Malawi, where the national electricity access rate stands at 11% (42% urban, 4% rural) [4]. At 365 MW, hydro fired electricity meets most of the country’s demand although standby diesel generators complement this capacity [4]. Off-grid RE exploitation remains very low. As of 2016, only 10.4 MW of solar were reported to have been installed although none of the installed systems are currently functional [5]. Electricity generation from off-grid wind systems can also not be traced except for the cases where wind was hybridized with solar to electrify six villages [5].

A closer look at the world’s most deployed off-grid RE systems reveals serious sustainability challenges, which are rendering the systems defunct. Among several factors, lack of technology and reverse engineering skills’ transfer, rigid bureaucracies, lack of community engagement prior to installations, lack of financing and comprehensive tariff collection strategy to make the projects self-financing, scarcity of spare parts and exposure of equipment to harsh environmental conditions are some of the challenges which are concomitant to the failure of the systems [6,7]. These challenges fall into the broader categories of technical, economic, social and environmental aspects.

Likewise, hybrid RE systems are challenged with multiple but conflicting sustainability factors which require thorough consideration before the systems are introduced to the real world conditions [8]. Objective decision making is therefore of paramount importance in the planning and deployment of the systems as it enhances the sustainability of the systems [8]. Suffice to say, one of the tools, which aids in rational decision-making is the Multi-Criteria Decision Analysis (MCDA). MCDA is a technique which helps in the selection of an optimal system based on its ability to satisfy several criteria [9]. The evaluation criteria encompasses the technical, economic, environmental and social aspects of the systems which form the basis for judgement [3]. Several methods, which are used in the performance of MCDA, have been discussed in literature. Elimination Choice and Translation Reality (ELECTRE), Preference Ranking Organization Method for Evaluations Enrichment (PROMETHEE), Analytical Hierarchy Process (AHP), Weighted Aggregate Sum Product Assessment (WASPAS), Grey Relation Method, Technique for Order of Preference by Similarity to the Ideal Solution (TOPSIS), Complex Proportional Assessment (CORPAS), Z-numbers, VIKOR, Strength, Weaknesses, Opportunities and Threats (SWOT) and MCDA Combined Fuzzy Method are some of the methods which have been presented [8–28]. However, in scenarios where comprehensive evaluations of the systems are desired, TOPSIS has been earmarked as the ideal method. TOPSIS draws strength from its ability to perform analyses using varied energy system alternatives and different criteria without overlaps at any point in the evaluation. This technique performs its evaluation by determining the relative closeness of each energy alternative to the ideal energy solution [9]. Ideally, the best energy system is supposed to have the shortest Euclidean distance from the ideal solution and the longest Euclidean distance from the negative ideal solution [9,21].

This general subject of sustainability analysis of RE systems using TOPSIS has never been dearth of research as a number of studies have been reported. To begin with, Diemuodeke et al [19] used TOPSIS to identify a best hybrid energy system among Diesel-PV-Wind, Diesel-Wind, Diesel-PV and Diesel-Battery energy systems for Nigeria’s coastal regions. Ranking of hydropower, geothermal, biofuel, hydrogen, wind and solar power generation systems using TOPSIS was also done in Turkey [22]. Another study by [23] capitalized on this technique to size hybrid solar PV-wind RE systems. TOPSIS was also used alongside SWOT method to identify an ideal sustainable energy alternative among large hydro, small hydro, wind, solar PV, concentrating solar, geothermal and biomass [20]. In order support policy formulation for energy planning, one study also used TOPSIS to evaluate the sustainability of 33 electricity generation systems [24]. In related work, TOPSIS and AHP were used to evaluate and select the best system among solar, wind, geothermal and biomass energies [25]. A multi-site approach to energy supply systems’ selection was also presented for Nigerian cities of Benin, Warri, Yenagoa, Port Harcourt, Uyo and Calabar [26]. The study used HOMER optimization results and TOPSIS algorithm to perform an optimal system assessment among eight energy alternatives namely; diesel, PV-battery, diesel-battery, wind-battery, PV-diesel-battery, wind-diesel-battery, PV-wind-diesel and PV-wind-diesel-battery [26]. This study therefore sought to apply the TOPSIS method to evaluate RE system alternatives, which were identified for rural electrification in Malawi. The systems were established through HOMER simulations. The study was based on three villages of Chigunda (CH), Mdyaka (MD) and Kadzuwa (KA).

2. Description of Study Locations

The three villages considered in this study are Chigunda, Mdyaka and Kadzuwa located in three different geographical regions of Malawi. Chigunda is located in Nkhotakota district in the central region of Malawi and lies within the geographical coordinates 12° 25’ 34.7” S and 034° 01’ 06.7” E. Mdyaka is in Nkhata Bay district in the northernregion and lies along 11° 47’ 09.5” S and 034° 13’ 39.0” E. Kadzuwa is a village in Thyolo district in the southern region of Malawi and lies within 15° 59’ 48.4” S and 035° 15’ 01.5” E. The annual average wind speeds and solar irradiation (GHI) are presented in color maps as shown Figure 1.

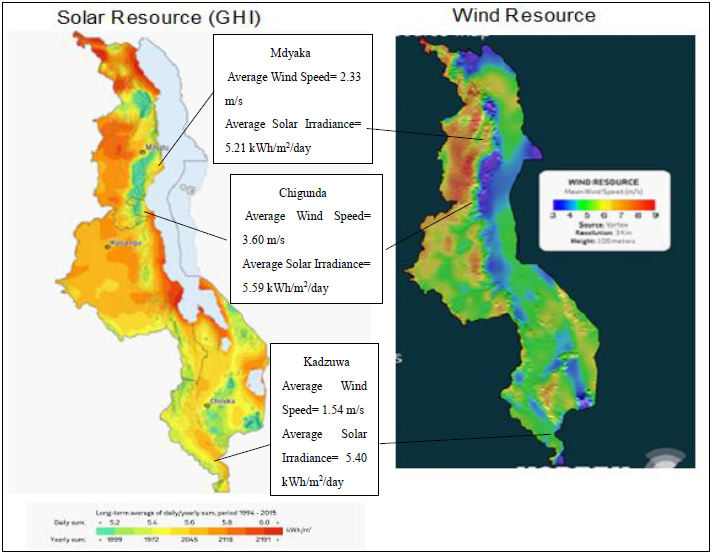Figure 1. Solar and wind resource maps for the study locations in Malawi

3. Methodology

Five hybrid energy system alternatives were considered in the MCDA process. These are namely; PV-Battery (PB), PV-Wind-Battery (PWB), PV-Diesel-Battery (PDB), Wind-Diesel-Battery (WDB) and PV-Wind-Diesel-Battery (PWDB). The energy systems and their representative performance scores, which were put under microscope, were derived from HOMER’s optimization results. The evaluation of the energy alternatives in this study proceeded in the subsequent stages.

3.1. Defining the Energy Alternatives and Criteria

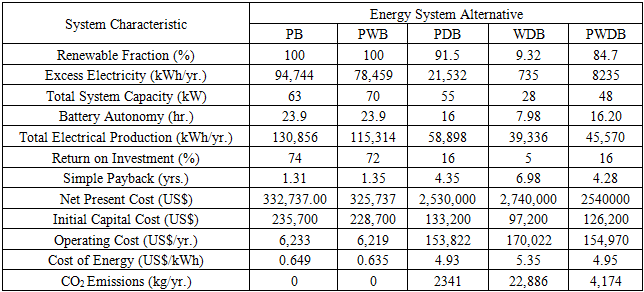
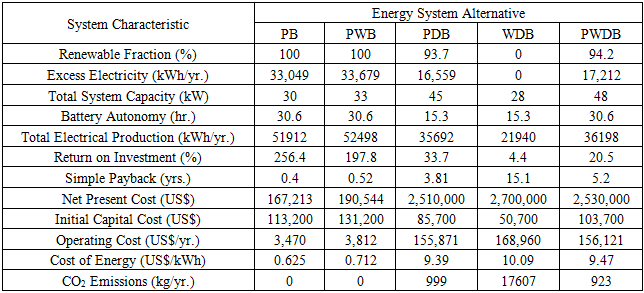
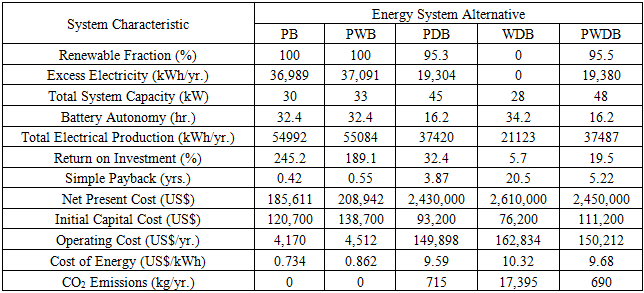
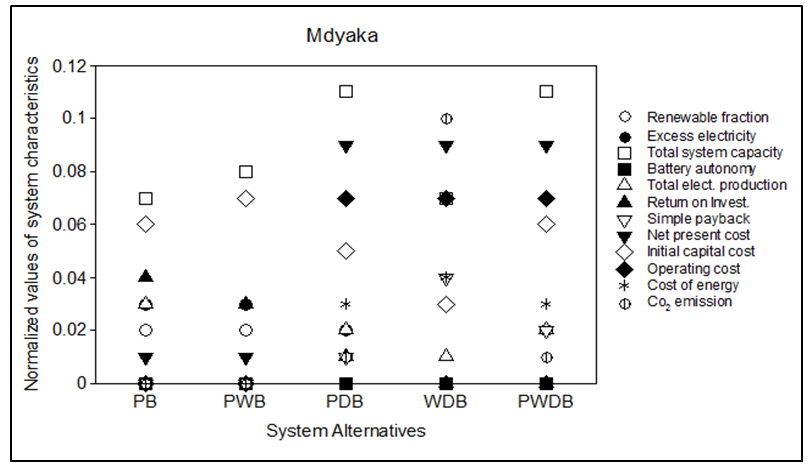
In the first step of the evaluation, the energy systems for each village were defined. The evaluation of the systems was based on the technical, economic and environmental criteria or attributes. Under these attributes, twelve sub-attributes or performance indicators were identified to assist in the analysis. The technical criterion was represented by renewable fraction, excess electricity, total system capacity, battery autonomy and total electrical production. Return on investment, simple payback, net present cost (NPC), initial capital cost, operating cost and cost of energy (COE) stood for the economic criterion. For the environmental attribute, the representative sub-attribute was the amount of carbon dioxide (CO₂) emissions. Inherently, some of these sub-criteria have positive and some have negative impact on an energy system. In principle, all costs and emissions have to be kept as low as possible in any energy enterprise and therefore, these were considered as negative [19]. In this regard, NPC, initial capital, COE, operating costs, excess electricity and CO₂ emissions were taken as negative attributes while renewable fraction, total system capacity, battery autonomy, total electricity production, return on investment and simple payback were considered to be positive attributes. The technical, economic and environmental sub-criteria considered in the study are described as follows;

Renewable Fraction (%): Quantifies the proportionate contribution of renewable power sources in satisfying the load.

Excess Electricity (kWh/yr.): This is the surplus electricity, which must be disposed of because it cannot serve the load or charge the battery storage.

Total System Capacity (kW): It relates to the cumulative size of the electricity generation components.

Battery Autonomy (hr.): A quantity obtained by calculating the ratio of the total battery size to the total electrical load.

Total Electrical Production (kWh/yr.): Represents the total amount of generated electrical energy in a year obtained through aggregation of individual component’s contribution.

Return on Investment (%): Compares the yearly savings in costs to the initial investment which was made.

Simple Payback (yrs.): The time taken to recoup the initially invested amount of money.

Net Present Cost (US$): This is the sum of the present value of installation and operation costs of an energy system over the course of its lifetime less the generated revenue over the same period.

Initial Capital Cost (US$): Total cost of installing an energy system when the project is being rolled out.

Operating Costs (US$/yr.): The difference between the total costs and revenues incurred in a year and the initial capital costs.

Cost of Energy (US$/kWh): The cost of producing 1 kWh of electricity.

CO₂ Emissions (kg): Yearly amount of carbon dioxide emissions resulting from operating an energy system. The optimization results from HOMER, which guided this work, are outlined in Table 1, Table 2 and Table 3.

Table 1. HOMER Optimization Results for Chigunda

Table 2. HOMER Optimization Results for Mdyaka

Table 3. HOMER Optimization Results for Kadzuwa

3.2. Formulation of the Decision Matrix

Central to the sustainability evaluation of RE alternatives using TOPSIS was the formulation of a deterministic decision matrix 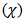with m energy alternatives and n criteria. The matrix members, x_ij, were perceived as the energy systems’ performance scores linking the energy alternatives to their criteria [9]. Specifying the scores for each sub-criterion resulted into matrices, which took the form of equation (1).

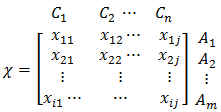(1)

In equation (1), C₁ to C_n represent the criteria or sub-criteria and A₁ to A_m stand for the energy alternatives under study and x₁₁ to x_ij indicate the scores.

3.3. Normalization of the Decision Matrix

The decision matrices were then subjected to normalization. This procedure helped in getting rid of the measurement units associated with the sub-criteria so that the analyses proceeded with dimensionless quantities [21]. This was done by using equation (2).

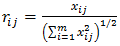(2)

3.4. Generating Weighted Normalized Matrix

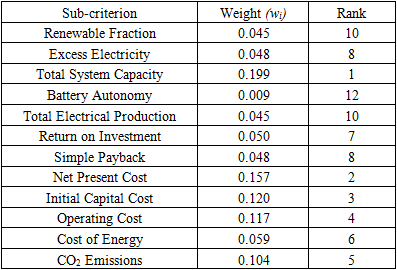
Weighted normalized matrices were generated using equation (3) through multiplication of the normalized decision matrix by the sub-criteria weights, which were determined using the Analytical Hierarchy Process (AHP). AHP generated sub-criteria weights (w_i) by comparing two sub-criteria at a time on a judgemental scale of 1-9. This was done in order to determine ranks which depicted how each sub-criterion was affecting an energy system [27].

(3)

The sub-criteria weights, which were used in all the villages, are presented in Table 4. As a general rule, the sum of the weights should be equal to 1 [28].

Table 4. Sub-criteria Weights from AHP Analysis

From the data presented in Table 4, it is evident that the determination of suitable energy systems was being influenced by the total system capacity designated to meet the communities’ electricity demand as this quantity was carrying more weight. However, net present, initial capital and operating costs were also having an impact.

3.5. Determination of Ideal and Negative Ideal Solutions

In order to determine the ideal (A^*) and negative ideal (A^-) solutions, equation 4 and 5 were employed respectively.

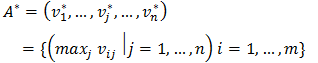(4)

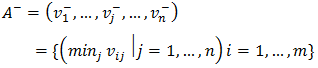(5)

In equation (4), A^* represents the ideal solution which is basically a set generated by choosing a largest member in each weighted normalized matrix’s row for the positive criteria and the smallest member in each weighted normalized matrix’s row for the negative criteria and combining them to form a single set [19]. To the contrary, A^- in equation (5) stands for the negative ideal solution obtained by choosing a smallest member in each weighted normalized matrix’s row for the positive criteria and the largest member in each weighted normalized matrix’s row for the negative criteria and combining them to form a single set [19].

3.6. Calculation of the Relative Separations

The Euclidean distances of each energy alternative from the ideal and negative ideal solutions were calculated by applying equation 6 and 7 respectively;

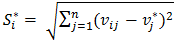(6)

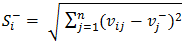(7)

Whereby S_i^* refers to the separation of each energy alternative to the ideal solution and S_i^- is the separation of each energy alternative to the negative ideal solution [28].

3.7. Determination of Relative Closeness of each Energy Alternative to the Ideal Solution

The relative closeness of each energy alternative to the ideal solution was computed through application of equation (8).

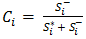(8)

From equation (8), C_i is the relative closeness of an energy alternative to the ideal solution (A^*).

4. Results

The results on the realization of the optimal energy system configurations suitable for deployment in Malawi’s rural communities of Chigunda, Mdyaka and Kadzuwa are presented. The results are based on TOPSIS’s step-wise matrix calculations, which were done in Microsoft Excel program.

4.1. Resultant Decision Matrices

Consolidation of the energy system alternatives and the sub-criteria values led to the formulation of decision matrices depicted in Tables (1,2,3).

4.2. Weighted Normalized Decision Matrices

The normalized values for the weighted decision matrices emanating from the systems’ characteristics for the three villages are presented graphically in Figures (2,3,4).

Figure 2. Normalized System Characteristics for Chigunda

Figure 3. Normalized System Characteristics for Mdyaka

Figure 4. Normalized System Characteristics for Kadzuwa

4.3. Ideal and Negative Ideal Solutions

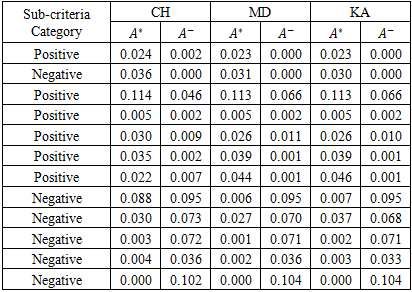
The ideal and negative ideal solutions for each village are presented in Table 5. The sub-criteria have been identified with their respective positive or negative impacts on the energy systems.

Table 5. Ideal and Negative Ideal Solutions for Chigunda, Mdyaka and Kadzuwa

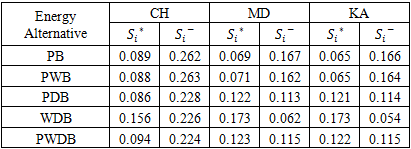
4.4. Relative Separations

The relative separations of each energy alternative from the ideal and negative ideal solutions are illustrated in Table 6 for Chigunda, Mdyaka and Kadzuwa.

Table 6. Ideal and Negative Ideal Solutions

4.5. Closeness to Ideal Solutions

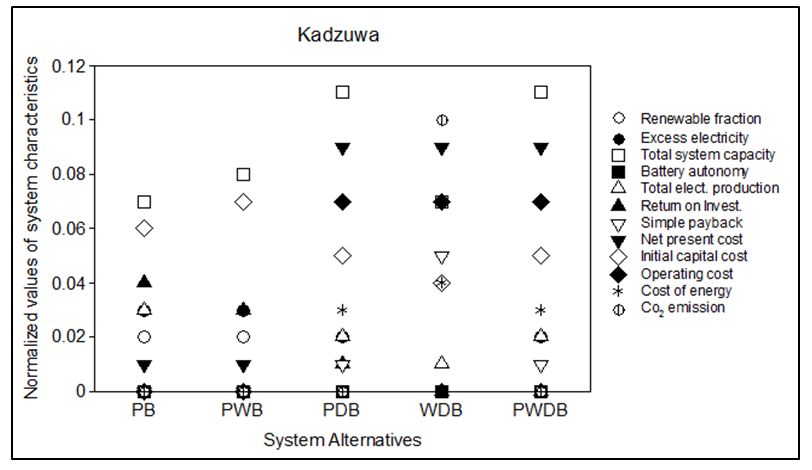
The relative closeness to ideal solution values (C_i) for each energy alternative for each village have been presented diagrammatically in the radar plot in Figure 5.

Figure 5. Ci values’ Radar Plot

5. Analysis and Discussion

The goal of this study was to identify an energy system for each village with the shortest Euclidean distance to the ideal solution (a system having a C_i value close to 1). In this regard, with reference to Figure 1, it is apparent that the system befitting deployment in Chigunda is the PV-Wind-Battery. This is so because this configuration has the closest distance to the ideal solution as evident by its C_i value of 0.749. This is seconded by the PV-Battery combination with a C_i value of 0.746. For Mdyaka, Figure 5 shows that the PV-Battery system is the best as it has the highest C_i value of 0.708. Following it is the PV-Wind-Battery configuration with a C_i value of 0.696. Finally, Figure 5 also indicates that for Kadzuwa, the PV-Battery configuration fits the assessment criteria by having a C_i value of 0.717. It is seconded by the PV-Wind-Battery configuration with C_i value of 0.715. One importation observation worth noting however is the absence of the diesel generator component in the ideal system configurations in all the villages. This is largely due to the high environmental footprint manifested by higher CO₂ emissions associated with the combustion of diesel and the higher operation costs, which come along with diesel generator usage. Viewing these results from a broader perspective, it can be hypothesized that on the overall, the PV-Wind-Battery system, which suit deployment in Chigunda, is the overall ideal solution for all the villages as it has the highest C_i value among all the systems under investigation.

Extending the scope of comparison also reveals notable variabilities with the results from literature. To begin with, in a study which set out to identify a suitable system among Diesel-PV-Wind, Diesel-Wind, Diesel-PV and Diesel-Battery under technical, economic and environmental criteria, it was established that the ideal system was the Diesel-PV-Wind which had a C_i value of 0.489 Diemuodeke et al [19]. This indicates some disparity with the results of the current study as not all the suitable energy alternatives contain a diesel generator component and the C_i value is lower when compared to those for all the suitable energy systems established by this study. In comparison with the results of the study by Diemuodeke et al [26], it is observed that for Benin, Yenagoa and Port Harcourt cities, the PV-wind-diesel-battery configuration was the suitable system with respective C_i value of 0.7226, 0.727759 and 0.728202. For Warri, Uyo and Calabar, the ideal system for deployment consisted of PV-wind-battery combination and had respective C_i values of 0.70036, 0.706276 and 0.685015. From these findings, it can also be observed that the findings for Benin, Yenagoa and Port Harcourt portray contrasting opinions with the results in this study based on both the ideal systems for deployment and the magnitudes of the C_i values. Much as the results on the optimal system configuration for Warri, Uyo and Calabar cities resonate well with the findings for Chigunda, the magnitudes of the C_i values are different. These differences in the findings are however inevitable due to the fact that different numbers of energy alternatives, criteria and sub- criteria were used and the magnitudes of the weights were also different.

6. Conclusions

The study aimed at establishing the optimal systems for deployment in rural areas of Malawi namely; Chigunda, Mdyaka and Kadzuwa. This was achieved with the aid of the TOPSIS algorithm, which is under the Multi-Criteria Decision Analysis. Five hybrid renewable energy systems were evaluated based on their ability to meet the technical, economic and environmental criteria. Based on the village-by-village analyses, the following key findings were established:

i. For Chigunda, the best system was the one having PV-Wind-Battery components. For Mdyaka, the optimal system comprised PV-Battery components and the same result held for Kadzuwa.

ii. System configurations with a diesel generator component were not preferred in the analyses.

With regard to the findings of this study, the following conclusions can be made:

i. Among several other existing methods for optimal system selection, TOPSIS can also act as powerful tool for evaluation and decision making on system selection. The tool can also be used to validate findings obtained when using different approaches.

ii. The multiplicity and multi-dimensional nature of TOPSIS qualifies it to be an effective energy planning tool for RE systems as the research has managed to establish the suitable energy systems for multiple locations through elimination of unfeasible systems.

ACKNOWLEDGEMENTS

The authors wish to acknowledge the Africa Center of Excellence in Phytochemical, Textiles and Renewable Energy (ACEII-PTRE) at Moi University for the financial support rendered towards this research.