1. Introduction

Economic Dispatch(ED) is one of the most important issues in power system operation. The main aim of ED is to minimize the operating cost of units, while satisfying certain constraints[1-3]. Thus, it can be stated that ‘the economic dispatchproblem is to define the generation level of each plant so that the total cost of generation and transmission is minimum for a prescribed schedule of loads’[1]. Certain conventional methods have been developed in the previous years for solving the ED problem. Some of these methods include lambda-iteration method, direct search method, Newton-Raphson method, efficient method[1,5-7]. In these methods assumption is made that the incremental cost curves of the generators are monotonically increasing piece-wise linear. However, in practical case the cost curves of the generators are highly non-linear and hence, such an assumption may not give accurate results.The nonlinearities in the generator operation are due to valve-point loading effects, prohibited operating zones, etc.[1].

In recent years certain artificial intelligence(AI) techniques such as Fuzzy Logic(FL)[8,9], Artificial Neural Network(ANN)[10-12], Genetic Algorithm(GA)[13-17], etc. have been successfully applied to the ED problems for units having non-linear cost functions. However, problem facedby FL is its low accuracy and large computational complexity.In ANN adopting an unsuitable sigmoidal function may suffer from excessive numerical iterations, resulting in huge calculations.

GA, which emulates from natural genetic operations, has emerged as a candidate for many optimization problems(including ED) due to its flexibility and efficiency. GA is a stochastic searching algorithm. In some GA applications, certain constraints including network losses and valve-point effects were considered for the practicability of the proposed method. Among these Walters and Sheble[13] presented a GA model for solving the ED problem including valve-point effects. Also Chen and Chang[15] presented a model that included network losses and valve-point effects. For an efficient solution to the ED problem, Chiang[17] and Amjady and Nasiri-Rad[18] presented improved and real-coded GA models respectively that can obtain high quality solutions in lesser time.

Although the GA model has been employed successfully in various optimization problems, recent researches show some difficulties with its implementation. GA shows quiet a large inefficiency when being implemented to objective functions in which the parameters to be optimized are highly correlated[19]. Also premature convergence is another problem that reduces its searching capability[20].

Particle swarm optimization(PSO) was developed by Kennedy and Eberhart in 1995 motivated by social behavior of organisms such as fish schooling and bird flocking[21]. It is one of the modern heuristic algorithms and has been found to be efficient and robust in solving non-linear problems[21-23]. The PSO technique can generate high quality solutions taking lesser computational time and providing a faster convergence as compared to other AI techniques[20,24-25,31]. In standard PSO(SPSO)[21], particles move around in the search space with the help of two accelerating components. One component, known as the cognitive component, controls the local exploration of the particles, while the second component, known as the social component, guides the global search capability of the particles. Kennedy and Eberhart[21] have shown that a high value of the local component will result in excessive exploration of the particles through the search space while a high value of the social component will result in a premature convergence of the particles. Various researchers[23,26,32-34] have found that the SPSO quickly finds a good local solution but gets stuck to it for rest of the iterations without a further improvement.

In order to overcome the above problems, a time varying acceleration coefficient[26] PSO(TVAC_PSO) strategy has been employed in this paper.The TVAC_PSO strategy finds a proper balance between the local and the global component and hence, the problem of premature convergence has been overcome to a much greater extent.The performance of the proposed TVAC_PSO strategy has been compared with SPSO[21], New PSO[27] and Anti-predatory PSO[28]. In order to show the superiority of the TVAC_PSO strategy over other strategies two test systems have been taken. The first test system consists of three generating units[13] while the second test system contains thirteen generating units[30]. A 24-hour short-term thermal generation schedule[4] has been presented for the three generator system with a peak demand of 850 MW to further add to the effectiveness of the proposed strategy.

2. Economic Dispatch with Valve-Point Loading(EDVPL)

The input-output characteristics(or cost functions) of a generator are approximated using quadratic or piece-wise quadratic functions, under the assumption that the incremental cost curves of the units are monotonically increasing piece-wise linear functions. However, real input-output characteristics display higher order nonlinearities and discontinuities due to valve point loading(VPL) in fossil fuel burning plants. The valve-point loading effect has been modeled in as a recurring rectified sinusoidal function[1].

The generating units with multi-valve steam turbines exhibit a greater variation in the fuel cost functions. The valve-point effects introduce ripples in the heat-rate curves. Mathematically, ED problem considering VPL[1] is defined as:Where,

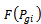is the fuel cost,

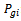is the active power generated,And 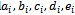are the fuel cost coefficients of the 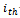generator.

The objective of the EDVPL problem is to determine the optimal power output 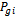of each of the generators for a total load demand of P_D. Total fuel cost 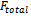for NG generators is minimized subject to the equality and the inequality constraints. Hence, the optimization problem can be stated as[1]:

Minimizesubject to the constraints given as:

a)the equality constraint–

b)the inequality constraint–

The total transmission losses P_L is a function of unit power outputs that can be expressed using B-coefficients as[1]

3. Review of Various PSO Strategies

Since the introduction of the PSO, various PSO based strategies have been successfully applied to deal with the ED problems. Some of the PSO strategies applied to the ED problems are presented briefly in this paper and their performances have been compared with the presented TVAC_PSO strategy.

3.1. Standard PSO(SPSO)

SPSO[21], as an optimization tool, provides a population-based search procedure in which individuals called particles change their position(states) with time. In a PSO system, particles fly around in a multi-dimensional search space. During flight, each particle adjusts its position according to its own experience and the experience of neighbouring particles, making use of the best position encountered by it and neighbours. The swarm direction of a particle is defined by the set of particles neighbouring the particle and its history experience. Instead of using evolutionary operation to manipulate the individuals, like in other evolutionary computational algorithms, each individual in PSO flies in the search space with a velocity which is dynamically adjusted according to its own flying experience and its companions flying experience. Let p and v denote a particle’s co-ordinate(position) and its corresponding flight speed(velocity) in a search space respectively. Therefore, each 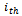particle is treated as a volume less particle, represented as 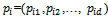in the d-dimensional space. The best previous position of the 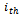particle is recorded and represented as 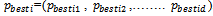The index of the best particle among all the particles is treated as global best particle, is represented as. The velocity for the 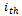particle is represented as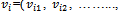

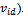The modified velocity and position of each particle can be calculated using the current velocity and the distance from 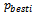to as shown in the following formulas,

In the above equation,c₁ and c₂ are known as the acceleration coefficients that pull each particle towards the 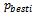and positions. Rand( ) and rand( ) are the uniform random numbers between[0,1]. The term rand( ) 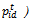is called the cognitive component. The term Rand( ) is called the social component. w is the inertia weight factor.Low values of acceleration coefficients allow particles to roam far from the target regions before being tugged back. On the other hand, high values result in abrupt movement towards, or past target regions. Hence, the acceleration constants c₁and c₂ are often set to be 2.0 according to past experiences.

A large inertia weight factor enhances global exploration while a low inertia weight factor helps in local search. Hence, a suitable selection of inertia weightprovides a balance between global and local explorations, thus requiring lesser iterations on average to find a sufficiently optimal solution. As originally developed[23], w often decreases linearly from about 0.9 to 0.4 during a run. In general, the inertia weight w is set according to the following equation,

Here 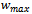is the maximum inertia weight, w_min is the minimum inertia weight, It is current no. of iterations, 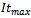is maximum no. of iterations.

3.2. New PSO(NPSO)

A new variation in the SPSO by splitting the cognitive component of the SPSO into two different components was proposed by Selvakumar and Thanushkodi[27]. The first component is called good experience component. That is, the particle has a memory about its previously visited best position. This component is exactly the same as the cognitive component of the SPSO. The second component is given the name bad experience component. The bad experience component helps the particle to remember its previously visited worst position. To calculate the new velocity, the bad experience of the particle is also taken into consideration. The new velocity update equation proposed is given by

The acceleration coefficients 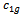and 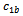help the particles to move towards their previous best positions and away from their previous worst positions respectively thereby increasing the exploration capability. 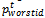is dimension d of the own worst position of the 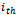particle until iteration t.

3.3. Anti-predatory PSO(APSO)

Another SPSO variant proposed by Selvakumar and Thanushkodi[28] included an anti-predatory property. The anti-predatory property, which is natural among particles, helps the swarm escape from the predators. This strategy models the predators as the worst result points and the new model is named anti-predatory PSO. The APSO is developed by splitting both the cognitive and the social behaviours of the SPSO. Here, along with the cognitive component, the social component is also split into global good experience and global bad experience components. The velocity update equation of the APSO model is given by

Here, 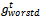is global worst position of member d until iteration t. The acceleration coefficient 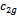helps the particles to accelerate towards their previous global best positions and 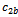helps the particles to move away from their previous worst positions. By using the bad experiences, particle always by-passes its previous worst positions. Hence, exploration capability is further enhanced.

4. Proposed PSO strategy

4.1. PSO with Time-varying Acceleration Coefficients (TVAC_PSO)

In this paper, the TVAC_PSO[26] strategy has been used to solve the EDVPL problems. Basic purpose of using the time varying acceleration coefficients is to improve the global exploration in the early part of the process and to enhance the convergence of the particles in the later stages of the process. This is done by varying the acceleration coefficients c₁ and c₂ with time in such a manner that the cognitive component reduces and the social component increases as iterations increase. In short, it can be stated that a large cognitive component and a small social component at the beginning of the process help the particles to explore the search space in a better way while a smaller cognitive component and a larger social component at later stages of the process allow the particles to converge to the global optima. The time varying acceleration coefficients are given as[29]:

4.2. Algorithm for TVAC_PSO

The sequential steps of the proposed TVAC_PSO strategy are given below.

Step1: Representation of the swarm- Since the decision variables of the economic dispatch problem are the real power generations, they are used to form the swarm. The set of real power output)(P_a)of all the generators is represented as the position of the particle in the swarm. For a system with NG generators, the particle position is represented as a vector of length NG. If there are NP particles in the swarm, the complete swarm is represented as a matrix as shown below:

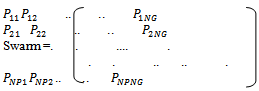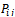Where is the j th position component of particle i and it represents the real power generation of generator j of the possible solution i.

Step2: Initialization of the swarm- The particles of the swarm are initialized randomly according to the limit of each generating unit. These initial particles must be feasible candidate solutions that must satisfy the operating constraints.

Step3: Evaluation of objective function- In order to satisfy the equality constraint(3), a generator is arbitrarily selected as a dependent generator 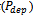whose generation is calculated as given below:

If the output of the dependent generator violates its lower limit, its output is set equal to its lower limit and if it violates its upper limit, its output is set equal to its upper limit. An output between the lower and upper limit is automatically acceptable.

The operating cost of individual generating unit is calculated using(1) and hence the total operating cost can be calculated using(2).

Step4: Initialization of best positions- In the PSO strategy, the particle’s best position, and global best position, are the key factors. The position with minimum objective function value is the particle’s best position. The best position out of all the is taken as .

Step5: Movement of the particles- Particles in the swarm are accelerated to new positions by adding new velocities to their current positions. The new velocity is calculated using the equation:

The positions of the particles are updated using(6).

Step6: Updating the best positions- If the evaluation value of each particle is better than previous the current value is set to. If the best is better than, this new value is set as. An objective function value at is set as.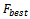

Step7: Stopping criterion- If the number of iterations reaches the maximum than the process is stopped and 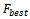is the minimum generation cost of the economic dispatch problem. Otherwise, the above process is repeated from step2.

5. Test Systems and Results

In order to show the superiority of the TVAC_PSO strategy over other PSO strategies discussed before, two test systems have been taken into consideration. The first test system consists of three generating units[13] with a load demand of 850 MW. The second test system has been taken from[30] which consist of 13 generating units with a load demand of 1800 MW. In this paper following parameters have been used for different PSO strategies: For NPSO, 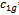= 1.6, 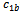= 0.4 and c₂= 2[27] have been used. For APSO, 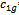= 1.6, 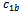= 0.4, 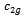= 1.8 and 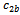= 0.2[28] have been adopted. For TVAC_PSO, [26] suggests that the values for c₁ should vary from 2.5 to 0.5 and from 0.5 to 2.5 in case of c₂ for best results.

Case1: Three-Generator system

For this system a population size of 20 has been taken with maximum number of iterations as 200. Losses have also been calculated using the loss coefficients given in[13] by using equation(4). Power generation of each generator, generating cost and losses corresponding to different PSO strategies have been shown in table 1. Convergence characteristics of each PSO model are shown in figure 1.

Table 1. Optimal results for 3 generator system including losses(PD= 850 MW) Power output(MW) SPSO NPSO APSO TVAC_PSO P1 399.3723 399.8393 400.4504 399.1669 P2 325.7694 326.5124 326.1388 326.8991 P3 150.6753 149.4418 149.1996 149.7331 Losses(MW) 25.8170 25.7936 25.7890 25.7991 Cost($/hr) 8453.6077 8449.3794 8443.5561 8440.7647

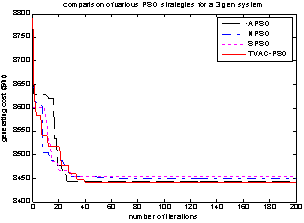Figure 1. Convergence characteristics of different PSO strategies(3-generator system)

Table 2. Optimal results for 13 generator system excluding losses(PD = 1800 MW) Power output(MW) SPSO NPSO APSO TVAC_PSO P1 538.5587 538.5042 539.1930 628.3185 P2 149.5459 298.7765 297.6252 223.5256 P3 224.3200 301.2419 312.2458 298.4228 P4 154.8511 60.0310 60.0280 60.0000 P5 109.8372 60.0000 60.0000 60.0000 P6 109.2508 60.0000 60.0000 60.0000 P7 60.0000 60.0120 60.0000 60.0000 P8 60.0000 60.0000 60.0000 60.1560 P9 60.0000 106.4773 160.7820 159.5771 P10 113.0114 40.1120 40.1050 40.0000 P11 73.2248 40.0000 40.0000 40.0000 P12 92.3999 55.2250 55.0210 55.0000 P13 55.0000 119.6200 55.0000 55.0000 Cost($/hr) 18156.0423 18133.1781 18105.7977 17989.0048

Table 3. Short-term thermal generation scheduling for case 1(Peak Demand= 850 MW) Time interval Demand(MW) P1(MW) P2(MW) P3(MW) Generation Cost($/hr) Losses(MW) 1 490 299.4235 165.8151 50.0000 5299.7132 23.8842 2 493 299.3172 167.5672 50.0000 5301.74552 23.8843 3 495 299.4662 169.4179 50.0003 5302.2856 23.8844 4 499 299.4661 173.1361 50.2878 5308.0231 23.8900 5 506 299.4662 180.0012 50.4255 5410.2912 23.8929 6 513 299.4676 187.4176 50.0000 5524.1834 23.8852 7 537 299.4662 174.7272 87.4010 5731.8712 24.5944 8 588 299.4662 175.3221 138.7424 6186.6227 25.5710 9 605 299.6675 181.3801 149.7331 6303.0091 25.7808 10 651 299.7988 177.9412 200.0000 6724.9173 26.7400 11 699 399.1993 175.7951 149.7962 7093.7716 25.7962 12 755 399.2602 182.4889 200.0000 7685.5134 26.7491 13 793 399.1993 262.4881 157.2503 8077.7387 25.9377 14 812 399.4145 324.7318 112.9521 8186.1096 25.0984 15 831 399.1993 312.8684 149.7303 8399.4645 25.7979 16 850 399.1669 326.8991 149.7331 8440.7647 25.7991 17 824 399.1407 251.6786 199.9326 8229.0647 26.7519 18 756 306.7987 325.2584 149.7331 7650.0912 25.7901 19 809 399.1993 323.1519 111.7237 8161.6756 25.0749 20 688 298.5953 314.3775 99.8666 7047.5423 24.8393 21 625 299.8796 250.4649 99.4834 6407.7079 24.8279 22 540 299.4893 173.9640 91.2135 5737.5865 24.6668 23 495 299.4662 169.4179 50.0003 5302.2534 23.8844 24 490 299.4235 165.1851 50.0000 5299.7175 23.8842

Case2: Thirteen-Generator system

For this system population size has been taken as 30 and maximum number of iterations as 200. Losses have been neglected for this case. Power generation of each unit and generating cost are shown in table 2. Corresponding convergence characteristics are shown in figure 2.

The effectiveness of the proposed TVAC_PSO strategy has been demonstrated with the help of the above two test systems. The optimal generation costs for the three-generator system and the thirteen-generator system using TVAC_PSO are $ 8440.7647 per hour(shown in bold in table 1) and $ 17989.0048 per hour(shown in bold in table 2) respectively which are lower as compared to the other PSO strategies discussed. The cost convergence characteristics for the three-generator system and the thirteen-generator system have been shown in figures 1 and 2 respectively. From these it can be easily deduced that the proposed TVAC_PSO strategy is better as compared to other PSO strategies.The TVAC_PSO strategy for the three-generator system has been used for finding the optimal short-term generation schedule for 24 time intervals each of 1 hour[4] with a peak demand of 850 MW. The optimal generation schedule has been shown in table 3.Load profile during 24 time intervals is shown in figure 3.

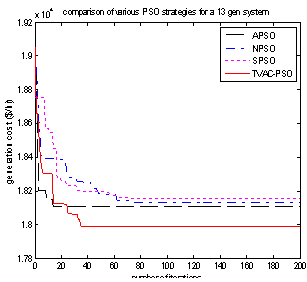Figure 2. Convergence characteristics of different PSO strategies(13-generator system)

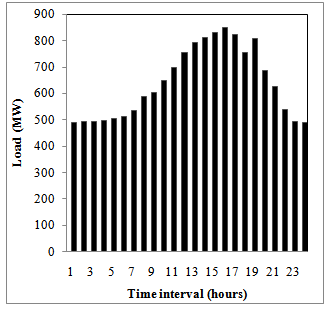Figure 3. Load profile during 24 time intervals(each of 1 hour)

6. Conclusions

In this paper, the TVAC_PSO strategy has been applied to EDVPL problems. A 24-hour short-term thermal generation scheduling has been presented to further add to the effectiveness of the proposed strategy. The performance of this strategy has been comparedwith SPSO, NPSO and APSO.Two standard test systems have been used for comparison. It has been found that by using the time varying acceleration coefficients better results are obtained in respect with the generation cost. The TVAC help in avoiding the premature convergence and thus providing a stable convergence. The TVAC_PSO strategy outperforms other PSO strategies, particularly for EDVPL problems, in terms of solution quality, stable convergence and stability.