-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Energy and Power
p-ISSN: 2163-159X e-ISSN: 2163-1603
2012; 2(2): 17-23
doi:10.5923/j.ep.20120202.03
EP-Based Optimisation for Estimating Synchronising and Damping Torque Coefficients
N. A. M. Kamari, I. Musirin, Z. A. Hamid, M. N. A. Rahim
Faculty of Electrical Engineering, Universiti Teknologi Mara, Shah Alam, Selangor, Malaysia
Correspondence to: I. Musirin, Faculty of Electrical Engineering, Universiti Teknologi Mara, Shah Alam, Selangor, Malaysia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper presents Evolutionary Programming (EP) based optimisation technique for estimating synchronising torque coefficients, Ks and damping torque coefficients, Kd of a synchronous machine. These coefficients are used to identify the angle stability of a system. Initially, a Simulink model was utilised to generate the time domain response of rotor angle under various loading conditions. EP was then implemented to optimise the values of Ks and Kd within the same loading conditions. Result obtained from the experiment are very promising and revealed that it outperformed the Least Square (LS) and Artificial Immune System (AIS) methods during the comparative studies. Validation with respect to eigenvalues determination confirmed that the proposed technique is feasible to solve the angle stability problems.
Keywords: Angle stability, Synchronising torque coefficient, Damping torque coefficient, Evolutionary Programming, Artificial Immune System
Cite this paper: N. A. M. Kamari, I. Musirin, Z. A. Hamid, M. N. A. Rahim, EP-Based Optimisation for Estimating Synchronising and Damping Torque Coefficients, Energy and Power, Vol. 2 No. 2, 2012, pp. 17-23. doi: 10.5923/j.ep.20120202.03.
Article Outline
1. Introduction
- Small signal stability analysis of power systems has become more important nowadays. Under small perturbations, this analysis predicts the low frequency electromechanical oscillations resulting from poorly damped rotor oscillations. The oscillations stability has become a very important issue as reported in [4-6]. The operating conditions of the power system are changed with time due to the dynamic nature, so it is needed to track the system stability on-line. To track the system, some stability indicators will be estimated from given data and these indicators will be updated as new data are received. Synchronising torque coefficients, Ks and damping torque coefficients, Kd are used as stability indicators. To achieve stable condition, both the Ks and Kd must be positive [1-3].Certain techniques have been proposed to estimate the values of Ks and Kd involving optimisation technique. Some techniques have been explored by means of frequency response analysis [6,7]. [3] decomposed the change in electromagnetic torque into two orthogonal components in the frequency domain. The two equations were expressed in terms of the load angle deviation then solved directly. Static and dynamic time domain estimation methods were also proposed in this study. Least Square (LS) method can be one of the possibletechniques in addressing the stable and unstable phenomena. It has been used as static parameter estimation [8]. However, several disadvantages have been identified in LS method. Amongst them are the long computation time and the requirement for data updating. It also requires monitoring the entire period of oscillation. Recently, optimisation algorithms such as Evolutionary Programming (EP) and Artificial Intelligent System (AIS) have received much attention in global optimisation problems. EP and AIS are heuristic population-based search methods that use both random variation and selection. The optimal solution search process is based on the natural process of biological evolution and is accomplished in a parallel method in the parameter search space. EP-based method has been applied in various researches in static [12-16] and dynamic system stability [17-19]. On the other hand, AIS optimisation approach is still new in power system compared to the EP. EP and AIS share many common aspects; EP tries to model the natural evolution while AIS tries to benefit from the characteristics of human immune system [20-22]. This paper presents an efficient online estimation technique of synchronising and damping torque coefficients in solving angle stability problems. It is based upon the population-based search methods that use both random variation and selection. The method is used to estimate synchronising torque coefficients, Ks, and damping torque coefficients, Kd, from the machine time responses of the change in rotor angle, Δδ(t), the change in rotor speed, Δω(t), and the change in electromechanical torque, ΔTe(t). The goal is to minimise the estimated coefficient error and the time consumed. The proposed EP technique is used to find the best solution of the formulated problem. Results obtained from the experiment using EP were compared with AIS and LS methods. Then, the results were verified with eigenvalues.
2. The System Model
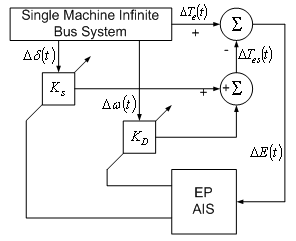
- A simplified block diagram model of the small signal performance is shown in Figure 1. In this representation, the dynamic characteristics of the system are expressed in terms of K constants with linearised single machine infinite bus (SMIB) system. This model is represented with some variables such as electrical torque, rotor speed, rotor angle, and exciter output voltage.
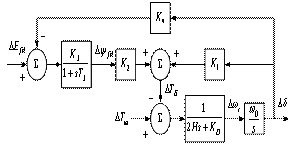 | Figure 1. Block diagram model of small signal performance. |
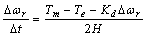 | (1) |
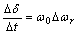 | (2) |
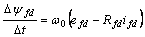 | (3) |
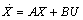
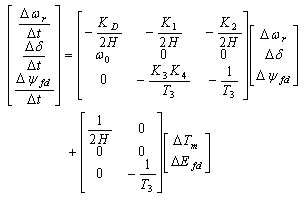 | (4) |
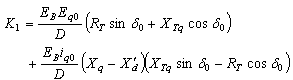 | (5) |
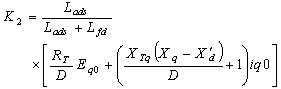 | (6) |
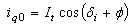 | (7) |
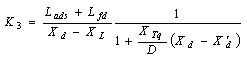 | (8) |
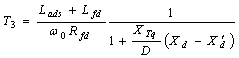 | (9) |
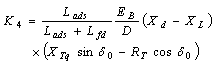 | (10) |
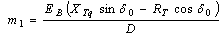 | (11) |
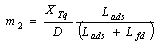 | (12) |
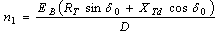 | (13) |
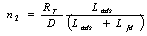 | (14) |
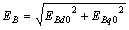 | (15) |
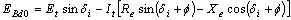 | (16) |
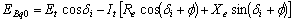 | (17) |
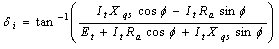 | (18) |
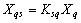 | (19) |
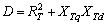 | (20) |
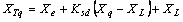 | (21) |
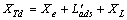 | (22) |
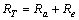 | (23) |
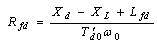 | (24) |
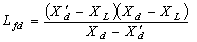 | (25) |
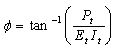 | (26) |
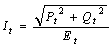 | (27) |
3. The System Model
- A single machine connected to infinite bus system is considered. The system comprises a steam generator connected via a tie line to a large system represented as infinite bus. The machine differential equations, the exciter equation, and the block diagram can be found in [1].The change of electromagnetic torque ΔTe(t) can be broken down into two components namely the synchronising torque, Ks and damping torque, Kd. The synchronising torque is in phase and proportional with the change in rotor angle, Δδ(t), while the damping torque is in phase and proportional with the change in rotor speed, Δω(t). The estimated torque, ΔTes(t) can be written as:
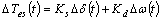 | (28) |
4. Evolutionary Programming
- The Evolutionary Programming (EP) is one of the evolutionary computing techniques that uses the models of biological evolutionary process to solve complex engineering problems. The search for an optimal solution is based on the natural process of biological evolution and is accomplished in a parallel method in the parameter search space. EP belongs to the generic fields of simulated evolution and artificial life. It is robust, flexible, and adaptable and it can yield global solutions to any problem, regardless of the form of the objective function.The advantages of EP over other conventional optimisation techniques can be summarised as follows [12-19]:(a) EP searches the problem space using a population of trials representing possible solutions to the problem and not a single point. This will ensure that EP has less possibility of getting trapped in local minima. Therefore, EP can reach to a global optimal solution.(b) EP uses performance index or objective function information to guide the search for solution. Therefore, EP can easily deal with non-smooth and non-continuous objective functions.(c) EP uses probabilistic transition rules instead of non-deterministic rules to make decisions. Moreover, EP is a kind of stochastic optimisation algorithm that can search a complicated and uncertain area to find the global minimum. This makes EP more flexible and robust than conventional methods.In the EP algorithm, the population has 2n candidate solutions with each candidate solution is an m-dimensional vector, where m is the number of optimised parameters. The EP algorithm can be described as:• Step 1 (Initialisation): Generation counter i is set to 0. n random solutions (xk, k=1, …, n) are generated. The kth trial solution xk can be written as xk=[p1 ,…, pm], where the lth optimised parameter pi is generated by random value in the range of [plmin, plmax] with uniform probability. Each individual is evaluated using the fitness J. In this initial population, minimum value of fitness, Jmin will be searched; the target is to find the best solution, xbest with the fitness, Jbest.• Step 2 (Mutation): Each parent xk produces one offspring xk+n. Each optimised parameter pl is perturbed by Gaussian random variable N (0, σl2). The standard deviation, σl specifies the range of the optimised parameter perturbation in the offspring. σl can be written as follows:
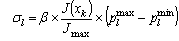 | (29) |
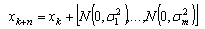 | (30) |
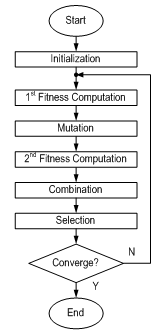 | Figure 2. Flowchart of EP |
5. Artificial Immune System
- Artificial immune system (AIS) approach to optimisation is more recent exploitation of natural phenomena in power system than EP. EP and AIS share many common aspects. Unlike the EP that tries to model the natural evolution, AIS tries to benefit from the characteristics of human immune system. Basic algorithm for AIS-based optimisation is called the Clonal Selection Algorithm (CSA) and it works as follows [20-22]:• Step 1: Initialisation; during initialisation, n random solutions (xk, k=1, …, n) are generated to represent the control parameters and determine the fitness, J.• Step 2: Cloning; population of variable x will be cloned by 10. As a result, the number of cloned population becomes 10n. Each individual of cloned population is evaluated using the J. Minimum value of fitness, Jmin will be searched; the target is to find the best solution, xbest with the best fitness, Jbest.• Step 3: Mutation; each individual clone is mutated. The mutation equation can be described as in equation (30) and (31).• Step 4: Ranking process; the population of matured clones in Step 2 and mutated clones in Step 3 are ranked based on fitness. The first n individuals with higher weights are selected along with their fitness as parents of the next generation. • Step 5: Convergence test; The search process will be terminated if one of the followings is satisfied:i It reaches the maximum number of generations.ii The value of (Jmax − Jmin) is very close to 0.If the process is not terminated, the iteration will repeat from Step 2 again. The flowchart of AIS is shown in Fig. 3.
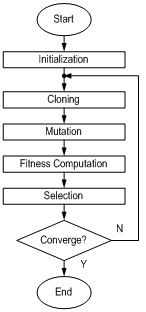 | Figure 3. Flowchart of AIS |
6. Least Square Method
- All the data of Δδ(t), Δω(t), and ΔTe(t) can be obtained from either offline simulation or online measurements. Following a small disturbance, the time responses of these three items are recorded. The least square (LS) method is then used to minimise the sum of the square of the differences between the electric torque, ΔTe(t) and the estimated torque, ΔTes(t). The error is defined as:
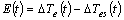 | (31) |
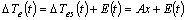 | (32) |
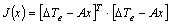 | (33) |
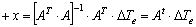 | (34) |
7. Test System
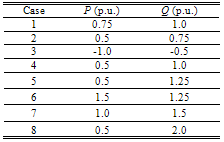
- In this study, performance evaluation of the EP for the estimation of Ks and Kd is compared with LS and AIS estimation methods. The evaluation is carried out by conducting several offline simulation cases on the linearised model of SIMB. In this study, block diagram as shown in Figure 1 is used for offline simulation to generate the required Δδ(t), Δω(t), and ΔTe(t) samples in MATLAB Simulink environment.
 | Figure 4. Estimating Ks and Kd using EP and AIS |
|
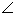 −36°Transmission line parameters:Re = 0.0, Xe = 0.65, XL = 0.16where Td0’ is the open circuit field time constant; Xd and Xq are the d-axis and q-axis reactance of the generator, respectively; Ra and Xd’ are the armature resistance and transient reactance of the generator, respectively; Re and Xe are the resistance and reactance of the transmission line, respectively; XL is the load reactance; Ksd and Ksq are the d-axis and q-axis of synchronising torque coefficients, respectively; and Et is the terminal voltage.Stable and unstable study cases are simulated using different types of disturbances. Data size is set to 20 seconds, while number of samples is set to 400 samples. Using Δδ(t), Δω(t), and ΔTe(t) as generated sample data, 2 sets of MATLAB files, EP and AIS-based simulation are developed. The simulation diagram is shown in Figure 4.In this study, eight sets of of Δδ(t), Δω(t), and ΔTe(t) samples are generated using offline simulation implemented in MATLAB Simulink. Those eight different loading conditions are tabulated in Table 1.During simulation, all parameters are adjusted until an optimal solution is obtained. The results of EP and AIS are compared with the LS solution.
−36°Transmission line parameters:Re = 0.0, Xe = 0.65, XL = 0.16where Td0’ is the open circuit field time constant; Xd and Xq are the d-axis and q-axis reactance of the generator, respectively; Ra and Xd’ are the armature resistance and transient reactance of the generator, respectively; Re and Xe are the resistance and reactance of the transmission line, respectively; XL is the load reactance; Ksd and Ksq are the d-axis and q-axis of synchronising torque coefficients, respectively; and Et is the terminal voltage.Stable and unstable study cases are simulated using different types of disturbances. Data size is set to 20 seconds, while number of samples is set to 400 samples. Using Δδ(t), Δω(t), and ΔTe(t) as generated sample data, 2 sets of MATLAB files, EP and AIS-based simulation are developed. The simulation diagram is shown in Figure 4.In this study, eight sets of of Δδ(t), Δω(t), and ΔTe(t) samples are generated using offline simulation implemented in MATLAB Simulink. Those eight different loading conditions are tabulated in Table 1.During simulation, all parameters are adjusted until an optimal solution is obtained. The results of EP and AIS are compared with the LS solution. 8. Simulation Results
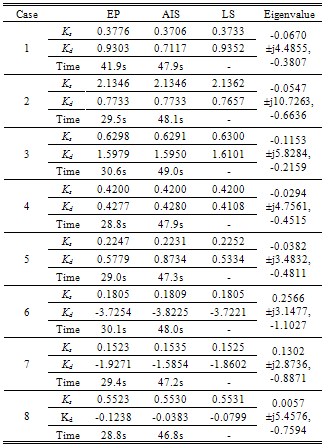
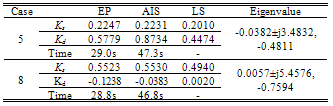
- In this study, eight sets of Δδ(t), Δω(t), and ΔTe(t) samples are generated using offline simulation of block diagram implemented in MATLAB Simulink. The samples of Δδ(t) data in graph forms are shown in Figure 5 until Figure 12. Different values of P and Q are used to simulate these cases. For verification, the eigenvalues for all cases have been calculated and written below of each graph. For cases in which all the eigenvalues are negative, they are stable. For cases that have positive eigenvalues, they are unstable.
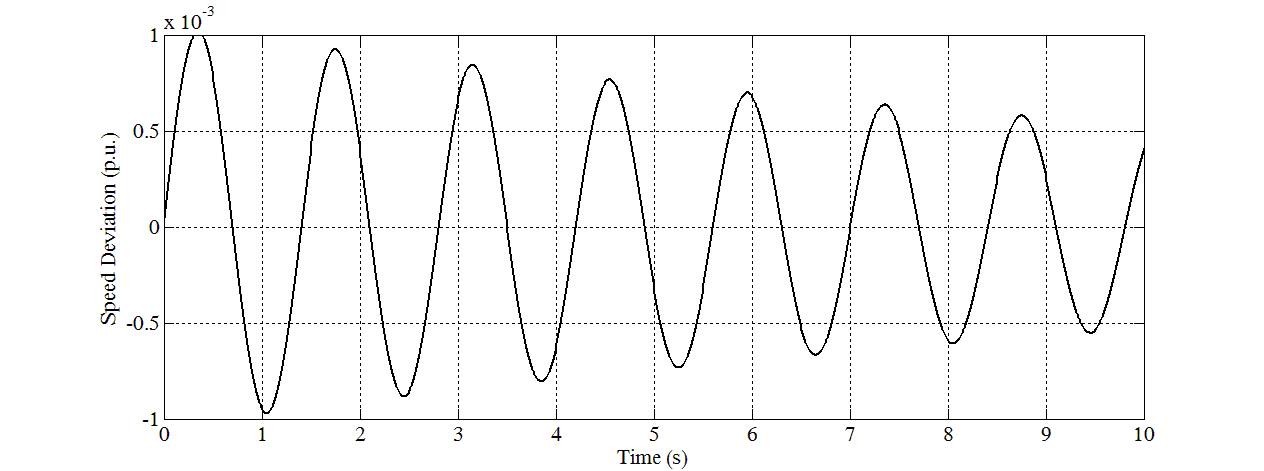 | Figure 5. Speed response for Case 1 |
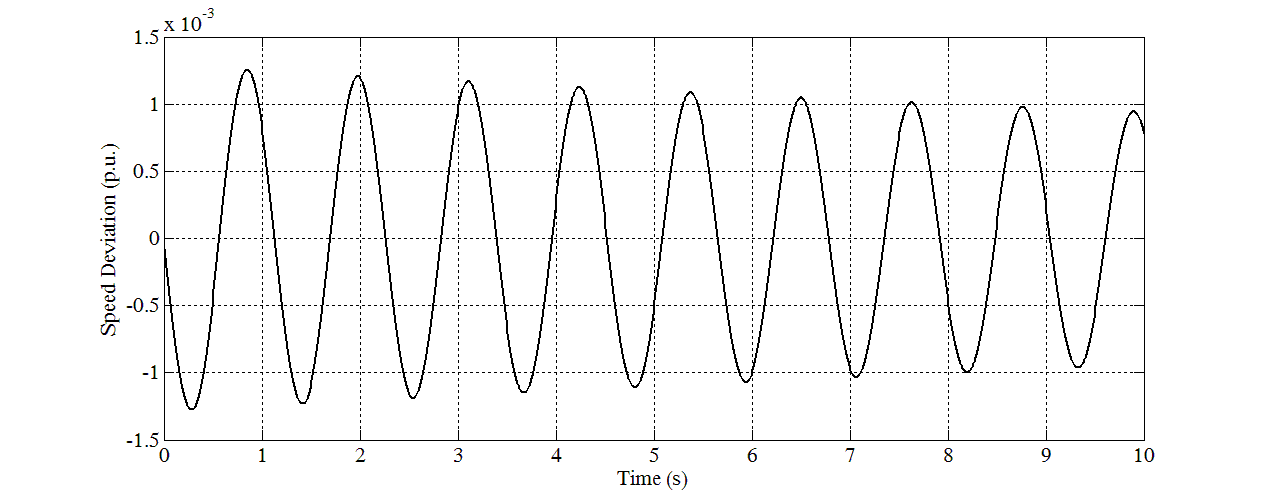 | Figure 6. Speed response for Case 2 |
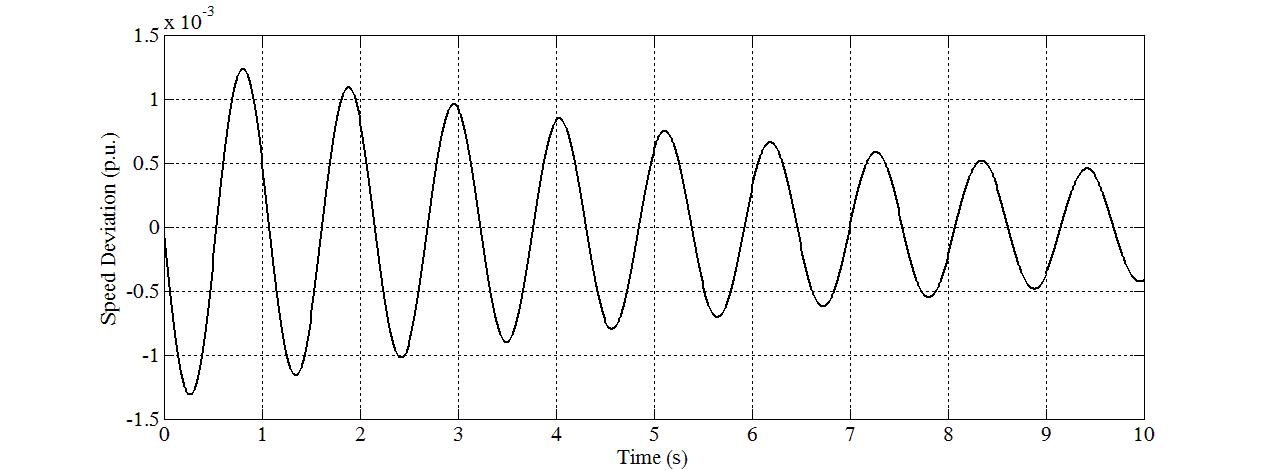 | Figure 7. Speed response for Case 3 |
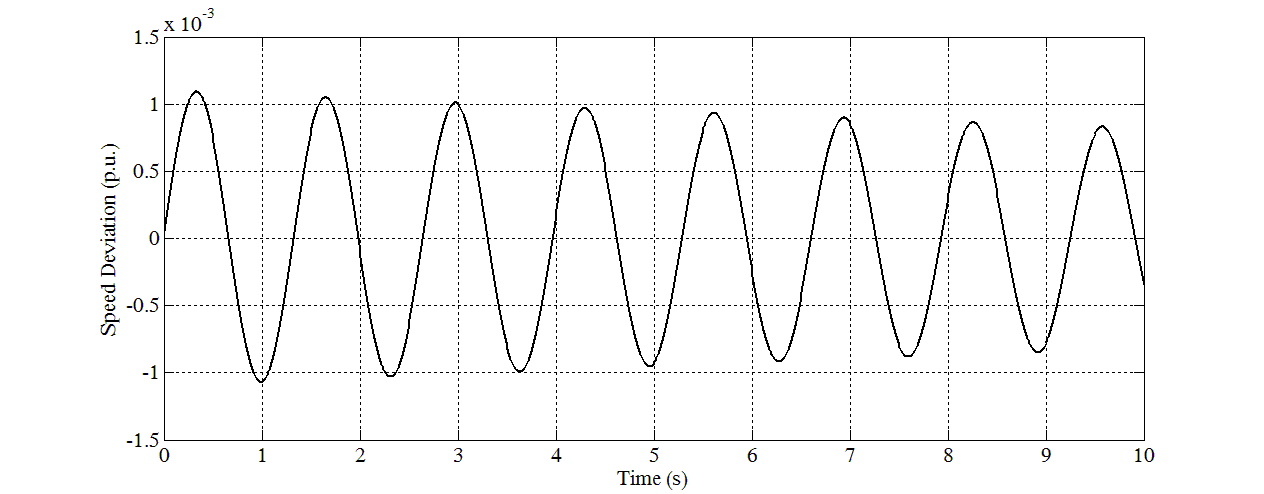 | Figure 8. Speed response for Case 4 |
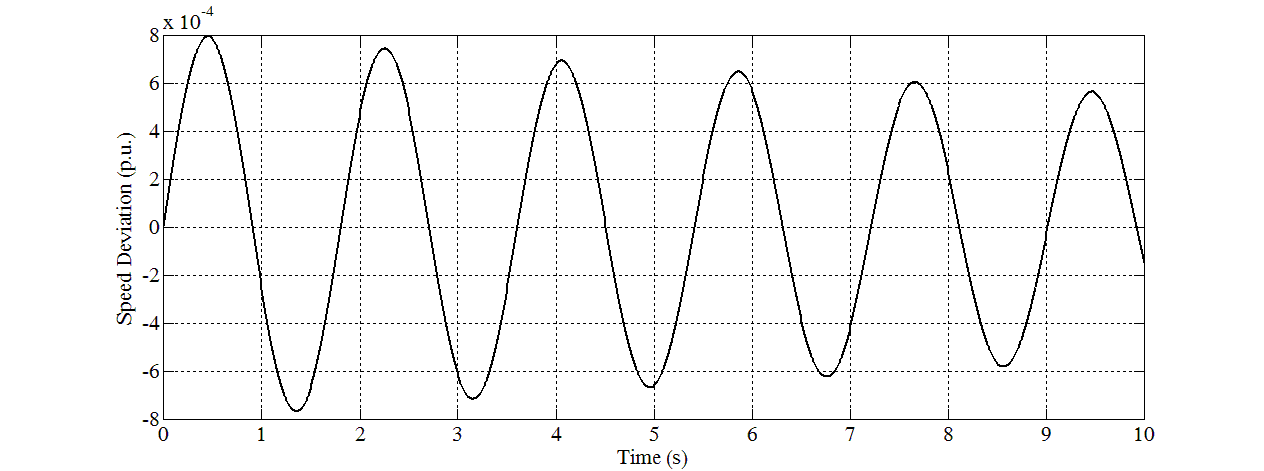 | Figure 9. Speed response for Case 5 |
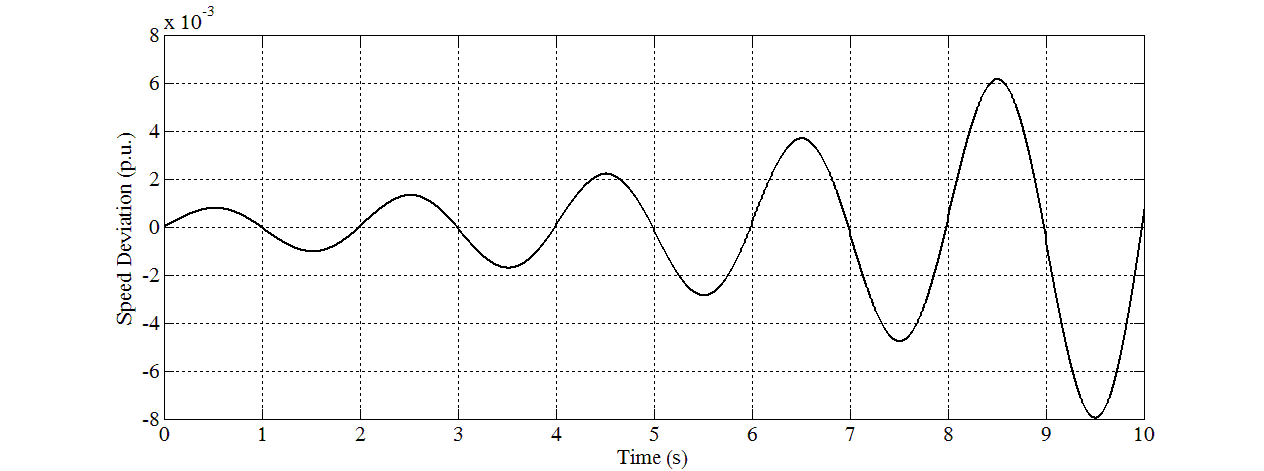 | Figure 10. Speed response for Case 6 |
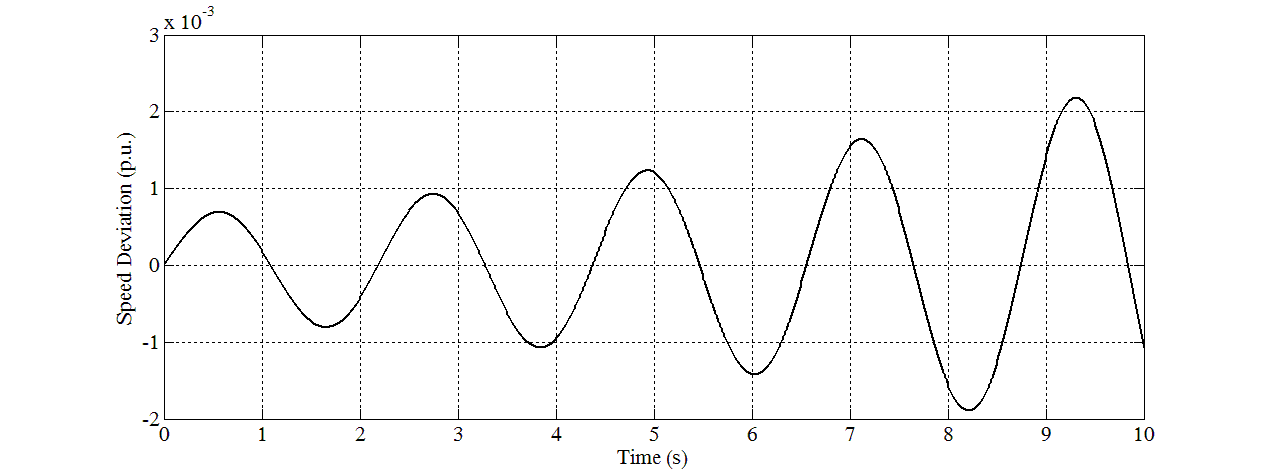 | Figure 11. Speed response for Case 7 |
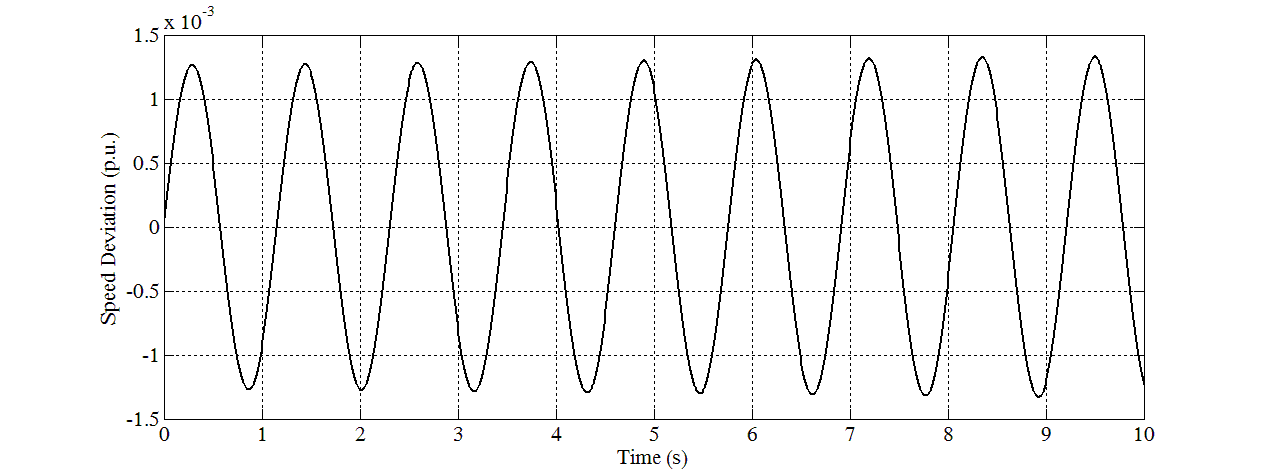 | Figure 12. Speed response for Case 8 |
|
|
9. Conclusions
- In this paper, three methods for accurate estimation of the synchronising and damping torque coefficients, Ks and Kd are presented. The performance of Evolutionary Programming (EP) is compared with the Artificial Immune System (AIS) and Least Square (LS) methods. In comparison with AIS and LS methods, EP offers several advantages. These include better data accuracy and 60% shorter computing time compared to AIS. EP is also not affected with bad data consumed in the system unlike the LS method that gives false decision on the stability. The proposed method can be considered a reliable and efficient tool in the area of power system stability analysis.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML