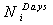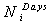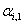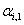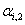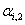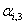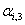Omid Ziaee 1, Ashkan Rahimi-Kian 2, Mohsen Parsa-Moghadam 3
1Sarakhs Branch, Islamic Azad University, Sarakhs, Iran
2School of Electrical and Computer Engineering, University of Tehran, Tehran, Iran
3Department of Electrical and Computer Engineering, Tarbiat Modares University, Tehran, Iran
Correspondence to: Omid Ziaee , Sarakhs Branch, Islamic Azad University, Sarakhs, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The electricity market restructuring has created new opportunities for customers to partner with utilities to alter their demand in response to electric system reliability needs or high prices. The consumer participation in wholesale energy markets tends to increase the electricity system reliability, reduce the electricity price volatility, and lower the average electricity prices paid by the consumers. This paper presents a new demand management program for the electric distribution companies (Dist Co.). It models and solves a profit maximization mathematical program for a Dist Co. subject to some constraints related to the customers’ costs of power interruptions, market price of electricity, and maximum amounts of interruptible loads by different consumers. The outputs of the mathematical program are the optimal load curtailments and optimal price tariffs for different customers that maximize the Dist Co’s profit function. The particle swarm optimization (PSO) and invasive weed optimization (IWO) algorithms are used to solve the non-linear mathematical program. A case study, for managing the power consumptions of some industrial firms in Iran, is presented and analyzed to show the applicability of the proposed demand management algorithm.
Keywords:
Demand Side Management Program, Distribution Company, Interruptible Load, Outage Cost, Profit Maximization
Cite this paper:
Omid Ziaee , Ashkan Rahimi-Kian , Mohsen Parsa-Moghadam , "An Optimal Pricing Policy for Interruptible Load Contracts in Power Markets: A Case Study for Iran", Energy and Power, Vol. 1 No. 1, 2011, pp. 14-20. doi: 10.5923/j.ep.20110101.03.
1. Introduction
The Power Utilities (PUs) are facing enormous financial risks in the new market environment. To mitigate these financial risks, new products have been developed. Among them is the interruptible load contract (ILC), which allows the PU to take a break on its obligation to provide a certain amount of electricity to a customer over a certain period of time[1]. A customer enters into an ILC with the PU to reduce a known percentage of its demand whenever needed by the PU, and in return it will gain discounts on its price tariffs and higher reliability for its demanded power. Researchers have shown that optimal demand management programs have major effects on preventing the price volatility in electricity markets[2,3]. As a matter of fact, the PU benefits from reducing its peak demand, saving on costly reserve, restoring the quality of its services and ensuring its reliability. The customer also benefits from reducing its demanded power through discounts on price tariffs and receiving more reliable power[4,5,6].A variety of voluntary demand management programs, including full interruption, equipment specific partial interruptions and programs that guarantee a certain “relief performance” was described in[7]. The authors define and compare three types of demand management programs:1) Firm Power Level Program, which defines a maximum power level (FPL) for each customer. During an interruption request, the customers in this program are required to reduce their demands down to their pre-agreed FPL.2) Agreed Relief Program, which has some similarities with the FPL program. When customers receive a relief request, they shed a predetermined amount of load from their demand level at the time of the curtailment request and have a sloping upper limit to their demand pickup during the requested curtailment period.3) Equipment Specific Interruption Program is different in a sense that there are no parameters to decide upon. However, the customer can decide what equipment to shut off upon request. Air conditioners and heaters would be among the best candidates since they put a big burden on the PU.A concept from game theory called “mechanism design” to develop demand management contracts for the PU based on its customers’ willingness to shed load was used in[8]. Their demand management contracts are largely governed by customer type (willingness to shed load) and customer location. The location value of each customer is calculated using the sensitivity method (sensitivity of line flows to the individual loads). Some customers are at more critical locations than the others that make them more important for the PU to sign interruptible load contracts with them.A leader-follower (cooperative game) based design of interruptible load contracts by PU in energy market environment was proposed in[9]. The amounts of load shedding and customer price tariffs were the decision variables of their game problem. Different market scenarios were discussed and simulated in their paper.In this paper, a new method for interruptible load contracts in power markets is proposed and tested with real case studies in Iran. By estimating the outage costs of some major industrial consumers, the optimal price tariffs and load shedding amounts are obtained through a nonlinear mathematical programming formulated for a Dist Co. to ensure that the results are optimum or not, we solved this problem by PSO and IWO algorithms.The rest of this paper is organized as follows: In section 2 we formulate the problem mathematically. In section 3, the model assumptions and solution method are explained. A case study, for managing the power consumptions of some industrial firms in Iran, is presented and analyzed in section 4. Section 5 concludes the paper.
2. Problem Formulation
A critical issue is, “How does the PU/Dist Co. distribute the amount of interrupted load among its customers to maximize its benefits, considering their interruption costs and their willingness to participate in the load management program?” To encourage the customers to participate in the load management program, discounted price tariffs are utilized to provide incentives for the customers. This problem is formulated under the following assumptions:A quadratic cost function is assumed for generators providing energy for Pus/ Dist Cos. in market. Therefore, the generation marginal cost is a linear function.Each customer’s normal load profile and the maximum total amount of load curtailment for each customer (at each hour as pre agreements) are considered known parameters.The outage cost [Rial1/kWh] for each customer who participates in the DMP is considered as a known parameter [10,11].For each customer, the consumption period is divided into three periods: off-peak, normal, and peak period. The outage cost for each customer is larger than the price tariff. Therefore, the number of days that the PU/Dist Co. discounts the price tariffs is considered a variable in the optimization process (by the power utility) in order to compensate the customers’ total incurred costs (by applying discounts to their price tariffs).The nomenclature of the model and equation parameters is as follows:Parameters: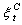 The non-discounted price tariff in period t [Rial/KWh] (t=1 is the off-peak, t=2 is the normal, and t=3 is the peak period).
The non-discounted price tariff in period t [Rial/KWh] (t=1 is the off-peak, t=2 is the normal, and t=3 is the peak period).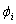 The outage cost of the ith customer [Rial/KWh].
The outage cost of the ith customer [Rial/KWh].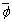 The maximum outage cost.
The maximum outage cost.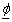 The minimum outage cost.
The minimum outage cost.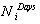 The number of days that customer-i receives discount in its price tariff.
The number of days that customer-i receives discount in its price tariff.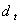 The duration of period t [hours].
The duration of period t [hours].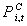 The normal power consumption of customer-i in period t [KW].
The normal power consumption of customer-i in period t [KW].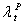 The market clearing price of electric energy (MCP) in period t [Rial/KWh].
The market clearing price of electric energy (MCP) in period t [Rial/KWh].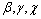 Coefficients of generation cost function.
Coefficients of generation cost function.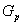 Amount of power generated by generation units.A positive value added to market clearing price to determine non-discounted tariff.Decision variables:
Amount of power generated by generation units.A positive value added to market clearing price to determine non-discounted tariff.Decision variables: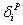 The amount of load interruption for customer-i [kW].
The amount of load interruption for customer-i [kW]. 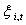 The customer-i discounted price tariff (as a reward for participating in the DMP) in period t [Rial/kWh].
The customer-i discounted price tariff (as a reward for participating in the DMP) in period t [Rial/kWh].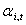 The discount factor for customer-i (in its price tariff) for period t.
The discount factor for customer-i (in its price tariff) for period t. 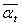 Maximum discount coefficient in period t.
Maximum discount coefficient in period t.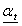 Minimum discount coefficient in period t.As mentioned before, the generation cost function is quadratic like Eq. (2.1):
Minimum discount coefficient in period t.As mentioned before, the generation cost function is quadratic like Eq. (2.1):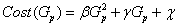 | (2.1) |
Therefore, marginal cost function is linear like Eq. (2.2).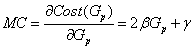 | (2.2) |
Where 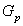 is the amount of power, and
is the amount of power, and 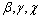 are coefficients which defined by generator units.The market clearing price,
are coefficients which defined by generator units.The market clearing price, 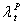 , is the point of intersection between marginal cost line and total amount of quantity demanded by customers,
, is the point of intersection between marginal cost line and total amount of quantity demanded by customers, 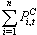 , as is shown in Figure. 1.
, as is shown in Figure. 1.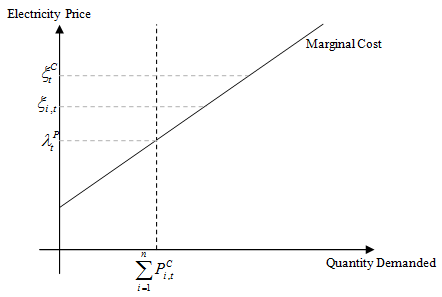 | Figure 1. Production cost function and market clearing price |
Therefore: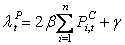 | (2.3) |
Selling power is profitable for PU/ Dist Co, if both discounted and non-discounted tariffs are higher than the market clearing price. So, it is assumed that non-discounted tariff is equal to market clearing price plus a positive value, shown in Eq. (2.4):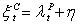 | (2.4) |
That the discounted tariff should be higher than market clearing price is assumed as a constraint in the solving procedure.To encourage the customers to participate in the proposed DMP, the maximum price discount belongs to the customer with the maximum outage cost. So, the relationship between the discount factor 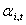 and the interruption cost
and the interruption cost 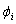 is assumed to be linear as shown in Figure. 2 and Eq. (2.5).
is assumed to be linear as shown in Figure. 2 and Eq. (2.5). 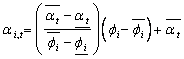 | (2.5) |
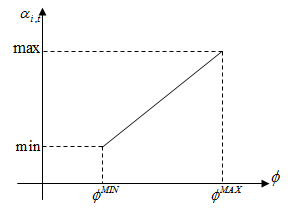 | Figure 2. A linear relation between the outage cost and the discount factor |
The discounted price tariff for each customer should be related to its load interruption amount (or participation in the DMP). Therefore, the discounted price tariff for customer-i is defined as follows: 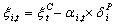 | (2.6) |
Each customer has three discount levels for off-peak, normal, and peak periods. This discount equals to the difference between the payments by non-discounted and discounted tariffs in each period. Therefore, the total monetary discount for each customer in each day (24 hours) is computed as follows: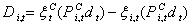 | (2.7) |
By placing Eq. (2.6) into Eq. (2.7) we have: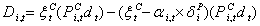 | (2.8) |
Therefore: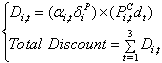 | (2.9) |
Besides, to encourage the customers to participate in the DMP, the total amount of monetary discount should be equal to or higher than their outage costs due to the load interruptions. This statement is shown in Eq. (2.10) and is used as a constraint to the PU/Dist Co. optimization: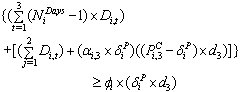 | (2.10) |
In Eq. (2.10), the total customer discount is divided into two parts. In the first part, a discount is given in the (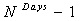 ) days even though the customer’s load is not curtailed; in the second part, the customer’s load is curtailed during the peak hours. The Ndays variable is set during the optimization process such that inequality (2.10) is satisfied. If one converts the inequality (2.10) into an equality constraint, then the Ndays variable could be analytically computed as follows:
) days even though the customer’s load is not curtailed; in the second part, the customer’s load is curtailed during the peak hours. The Ndays variable is set during the optimization process such that inequality (2.10) is satisfied. If one converts the inequality (2.10) into an equality constraint, then the Ndays variable could be analytically computed as follows: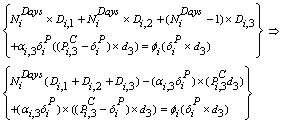 | (2.11) |
By placing Eq. (2.9) into Eq. (2.11) we have: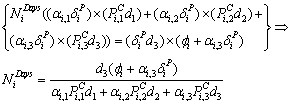 | (2.12) |
According to Eq. (2.12), the 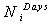 is a function of other parameters and decision variables.The objective function of the power utility is to maximize the total profit from selling power to its n customers as shown in equation (2.13),
is a function of other parameters and decision variables.The objective function of the power utility is to maximize the total profit from selling power to its n customers as shown in equation (2.13), 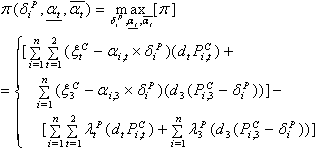 | (2.13) |
Since, 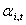 is a function of
is a function of 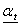 and
and 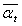 , the utility’s profit will be a function of
, the utility’s profit will be a function of 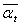 ,
, 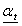 and
and 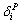 .The objective of the power utility is to maximize its total profit with respect to the following constraints:
.The objective of the power utility is to maximize its total profit with respect to the following constraints: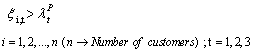 | (2.14) |
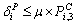 | (2.15) |
Constraint (2.14) shows that the customers’ discounted price tariffs should be higher than the market price of energy, such that selling power becomes profitable for the PU/Dist Co. Constraint (2.15) is utilized in order to limit the amount of interrupted load to a pre agreed percentage by the customer; 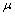 is the limiting load curtailment percentage.
is the limiting load curtailment percentage.
3. The Solution Approach
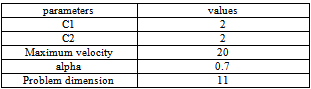
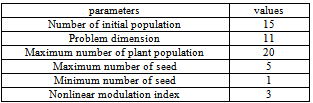
To solve the above formulated DMP problem (for a power utility), two evolutionary algorithms are used; the Particle Swarm Optimization (PSO)[12] and the Invasive Weed Optimization (IWO)[13].These two methods are utilized to find the optimal values of 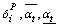 for each customer of a PU. The PSO is an extremely simple search method that seems to be very effective for optimizing a wide range of problems related to power systems[14,15,16]. The IWO is a stochastic numerical algorithm inspired from weed colonization. The IWO has shown successful results in many practical applications like optimization and analysis of electricity markets dynamics[17]. As the purpose of this paper is not to discuss about the details of these two algorithms, here only the parameters of these two algorithms are defined. For more information about the details of these algorithms see[12,13]. The chosen parameters for both the PSO and IWO algorithms are given in Tables 1 and 2. These parameters are selected according to[12], and[13], respectively.
for each customer of a PU. The PSO is an extremely simple search method that seems to be very effective for optimizing a wide range of problems related to power systems[14,15,16]. The IWO is a stochastic numerical algorithm inspired from weed colonization. The IWO has shown successful results in many practical applications like optimization and analysis of electricity markets dynamics[17]. As the purpose of this paper is not to discuss about the details of these two algorithms, here only the parameters of these two algorithms are defined. For more information about the details of these algorithms see[12,13]. The chosen parameters for both the PSO and IWO algorithms are given in Tables 1 and 2. These parameters are selected according to[12], and[13], respectively.Table 1. The PSO algorithm parameters.
 |
| |
|
Table 2. The IWO algorithm parameters
 |
| |
|
After completing the optimization process, each customer’s load interruption during the peak demand hours, his/her discounted price tariff for each demand period (t=1,2,3) and the number of discount days for him/her are obtained. Also, the total discount value and total outage cost for each customer during the demand management period are compared.
4. Iran’s Case Study
In this section a real case study for managing the power consumptions of five industrial firms in Iran, is presented and analysed to show the applicability of the proposed demand management algorithm. The main problem is formulated as given in section 2. Considering five customers makes a 11-dimension solution space (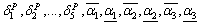 ).The
).The 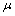 coefficient in (2.15) is set to 0.2, which means that the PU may interrupt up to a maximum of 20% of each customer’s load. The
coefficient in (2.15) is set to 0.2, which means that the PU may interrupt up to a maximum of 20% of each customer’s load. The 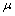 in (2.4) is set to 100 Rials, which means that non-discounted tariff is 100 Rials more than market clearing price. By evaluating the situation and data for this case study
in (2.4) is set to 100 Rials, which means that non-discounted tariff is 100 Rials more than market clearing price. By evaluating the situation and data for this case study 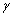 is set to 12 for all three periods.
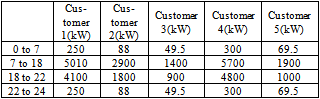
is set to 12 for all three periods. 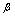 is set to 0.124, 0.0135, and 0.0275 for off-peak, normal, and peak periods respectively. The five customers’ loads during the peak, normal, and off-peak hours are given in Table 3 and Figure. 3.
is set to 0.124, 0.0135, and 0.0275 for off-peak, normal, and peak periods respectively. The five customers’ loads during the peak, normal, and off-peak hours are given in Table 3 and Figure. 3.Table 3. The customers’ normal load patterns in 24 hours
 |
| |
|
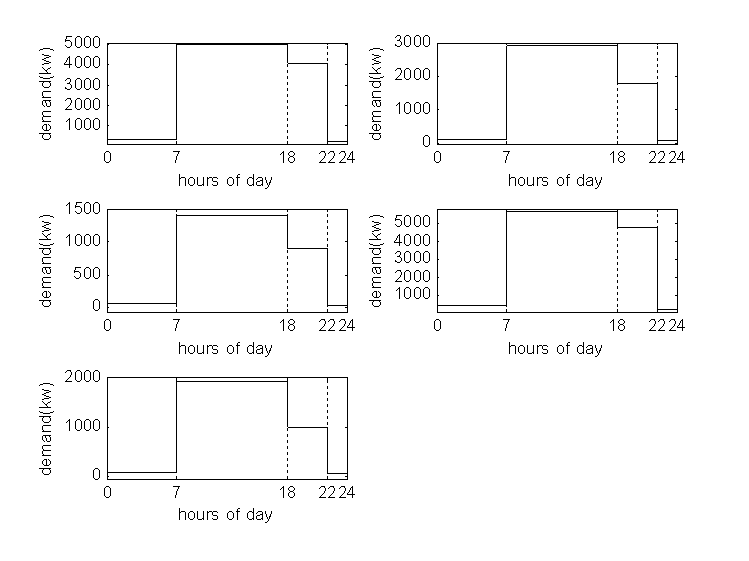 | Figure 3. The daily normal load profiles for five different customers |
To construct the model, it is essential to have the power outage costs for these five customers. In[10] and[11] the power outage costs for some industrial sectors in Iran were estimated. Five of those customers were selected for the case study of this paper. The outage costs, amounts of load interruptions (or load shedding) and the number of days with discounted price tariffs are presented in Table 4.Each of the PSO and IWO algorithms was run for 50 replications and 1000 cycles, and the solutions with the highest fitness values were chosen for presentation. The optimal profit values for the PU were obtained as 21,983,635 Rials by the PSO and 21,983,630 Rials by the IWO. According to the results of Table 4, customer 5 with the maximum outage cost, has the minimum amount of curtailed load. Customer 3 has the minimum outage cost, but due to the limitation on its load interruption, it does not have the maximum level of load shedding. | Table 4. The outage costs, optimal load curtailments and optimal Ndays for all customers. |
| | | Customer 1 | Customer 2 | Customer 3 | Customer 4 | Customer 5 | | Outage cost (Rial/kwh) | 7495 | 8227 | 7232 | 8624 | 17574 | | Load shedding by PSO (kw) | 308.48 | 184.25 | 148.27 | 309.63 | 49.36 | | Load shedding by IWO (kw) | 318.23 | 247.19 | 117.85 | 270.27 | 46.46 |
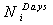
by PSO | 19 | 39 | 78 | 16 | 63 |
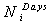
by IWO | 19 | 40 | 81 | 16 | 59 |
|
|
| Table 5. The total outage costs and total monetary discounts for all customers. |
| | | Customer 1 | Customer 2 | Customer 3 | Customer 4 | Customer 5 | | Total outage cost by PSO (Rial) | 9247970 | 6007688 | 4289431 | 10505035 | 3469879 | | Total outage cost by IWO (Rial) | 9368951 | 8051630 | 3395835 | 9091299 | 3261993 | | Total discount value by PSO (Rial) | 9300766 | 6063149 | 4291661 | 10681257 | 3480054 | | Total discount value by IWO (Rial) | 9540238 | 8134544 | 3409161 | 9323298 | 3265985 |
|
|
| Table 6. The discounted price tariffs for all customers for three demand periods. |
| | | Customer 1 | Customer 2 | Customer3 | Customer 4 | Customer 5 | | Peak(Rial/kwh)-PSO | 743.77 | 745.18 | 747.33 | 740.9 | 744.94 | | Peak(Rial/kwh)-IWO | 743.71 | 743.78 | 747.91 | 742.41 | 745.63 | | Normal(Rial/kwh)-PSO | 545.69 | 547.26 | 547.98 | 545.23 | 548.69 | | Normal(Rial/kwh)-IWO | 545.99 | 546.55 | 548.57 | 546.02 | 548.53 | | Off-Peak(Rial/kwh)-PSO | 233.28 | 259.74 | 268.05 | 231.96 | 287.81 | | Off-Peak(Rial/kwh)-IWO | 224.66 | 241.33 | 272.13 | 235.77 | 288.63 |
|
|
| Table 7. The optimal discount factors for all customers in three demand periods. |
| | | Customer 1 | Customer 2 | Customer3 | Customer 4 | Customer 5 |
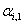
(Off-Peak)-PSO | 0.2163 | 0.2185 | 0.2155 | 0.2197 | 0.247 |
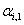
(Off-Peak)-IWO | 0.2367 | 0.2373 | 0.2365 | 0.2376 | 0.2448 |
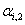
(Normal)-PSO | 0.01398 | 0.01489 | 0.01365 | 0.01539 | 0.02657 |
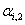
(Normal)-IWO | 0.01259 | 0.01397 | 0.01209 | 0.01472 | 0.03162 |
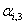
(Peak)-PSO | 0.02018 | 0.02615 | 0.01804 | 0.02939 | 0.1024 |
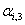
(Peak)-IWO | 0.01978 | 0.02517 | 0.01784 | 0.0281 | 0.09407 |
|
|
The last rows in Table 4 show the optimum number of days that the PU/Dist Co.should give discount in its electricity tariffs to compensate for the customers’ outage costs.The total outage costs and total price tariff discounts for each customer are given in Table 5. As shown in this table, customer 5 gets the minimum total price discount due to his/her lowest participation in the DMP. Using Eq. (2.12), the 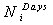 is computed for each customer and if its value was non-integer then it will be rounded up to the closest integer.The optimal electricity price tariffs are also given in Table 6. The discounted price tariffs are higher than the market price of electricity to ensure the positive profit for the PU.Table 7 shows the discount coefficients for 5 customers. These discount factors are related to the outage costs, meaning that the discount factors for the customers with higher outage costs are higher than those for the customers with lower outage costs (assuming that all of them participate in the DMP by the PU). To illustrate the cost of electricity for each customer, Figure. 4 to Figure 6 show these costs before and after participating in the demand management program. These figures show the average cost in
is computed for each customer and if its value was non-integer then it will be rounded up to the closest integer.The optimal electricity price tariffs are also given in Table 6. The discounted price tariffs are higher than the market price of electricity to ensure the positive profit for the PU.Table 7 shows the discount coefficients for 5 customers. These discount factors are related to the outage costs, meaning that the discount factors for the customers with higher outage costs are higher than those for the customers with lower outage costs (assuming that all of them participate in the DMP by the PU). To illustrate the cost of electricity for each customer, Figure. 4 to Figure 6 show these costs before and after participating in the demand management program. These figures show the average cost in 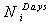 for each customer in three demand periods. As shown in these figures, the cost of electricity for each customer gets lower by participating in the DMP and therefore their outage costs are compensated.
for each customer in three demand periods. As shown in these figures, the cost of electricity for each customer gets lower by participating in the DMP and therefore their outage costs are compensated.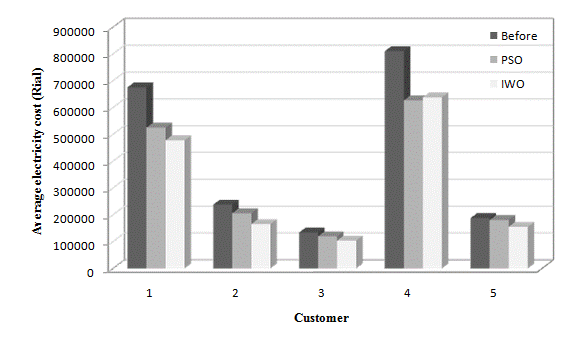 | Figure 4. The average electricity costs for all customers in off-peak period before and after participating in the DMP by the PU/Dist Co |
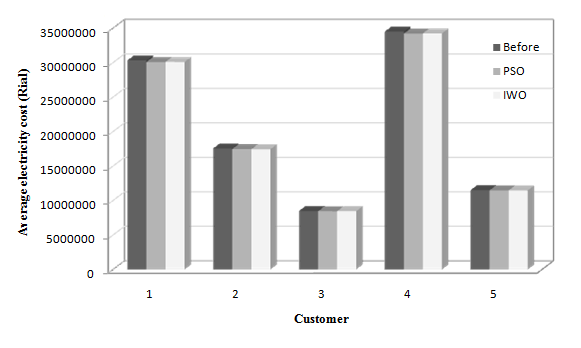 | Figure 5. The average electricity costs for all customers in normal period before and after participating in the DMP by the PU/Dist Co |
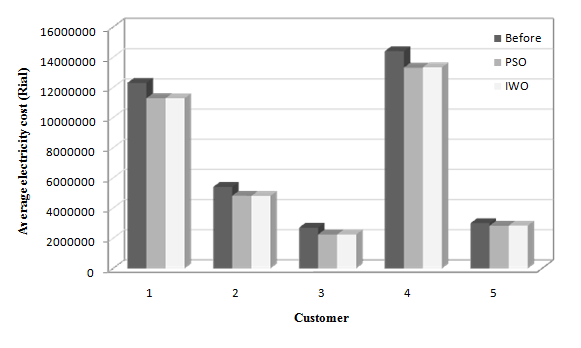 | Figure 6. The average electricity costs for all customers in peak period before and after participating in the DMP by the PU/Dist Co |
5. Conclusions
In this paper, a novel mathematical programming was developed for optimal demand management by a typical power utility or distribution company. In the developed DMP model the customers’ power outage costs, load shedding amounts and electricity price tariffs were considered as the decision variables for the PU to come up with optimal load shedding and price tariffs in order to encourage its customers to participate in its designed DMP for the benefits of both sides (to create a win-win situation for both sides). The developed DMP model was solved by two optimization algorithms, the PSO and IWO (as two powerful tools for numerical optimization of complex mathematical programs). A case study was run for five typical factories in Iran (with estimated power outage costs). The DMP model was applied for these five companies and the optimal load shedding amounts, optimal price tariffs (for three demand periods), optimal number of days for the DMP that get price discounts, and the amounts of monetary savings for participating in the developed DMP were computed and presented in different tables to show the applicability of the proposed DMP.In our future studies, we will try to develop a dynamic demand management program considering the electricity market dynamics and uncertainties.
Notes
1. Rial is the Iranian national currency. Where currently one dollar equals approximately 10,000 Rials
References
| [1] | Baldick R, Kolos S, Tompaidis S. Interruptible Electricity Contracts from an Electricity Retailer's Point of View: Valuation and Optimal Interruption. Journal of Operation Research 2006; 54 (4): 627-642 |
| [2] | Bjorgan R, Liu C, Lawarree J. Financial risk management in a competitive electricity market. IEEE Transactions on Power Systems 1999; 14 (4): 1285– 1291 |
| [3] | Strbac G, Kirschen D. Assessing the competitiveness of demand-side bidding. IEEE Transactions on Power Systems 1999; 14 (1): 120– 125 |
| [4] | Kamat, Rajnish, Oren S. Exotic options for interruptible electricity supply contracts. Journal of Operations Research 2002; 50: 835-850 |
| [5] | Boisvert, Cappers, Neenan. The benefits of customer participation in wholesale electricity market. Electric Journal 2002; 15 (3): 41-51 |
| [6] | Sheen J. Incentive pricing and economic profitability of load management program.Journal of Energy 2006; 31 (12): 2193-2209 |
| [7] | Fahrioglu M, Alvarado F. The Design of Optimal Demand Management Program. Available at |
| [8] | Fahrioglu M, Alvarado F. Designing Cost Effective Demand Management Contracts Using Game Theory. Available at |
| [9] | Rahimi Kian A, Keyhani A. Incentive control of spininig reserve in electricity multi markets. Decision Support Systems 2004; 40: 473-481 |
| [10] | Ziaee O, Rahimi Kian A, Parsa M. Estimation of Power Interruption Cost Using Causality Model for Industrial Sector in Iran. In: Proceedings of the IEEE PES general meeting, Calgary, Canada. 2009 |
| [11] | Amini F. et al., 2004. An investigation of electricity outage cost for industrial sector in Iran. Niroo Research Institute (NRI). Project PENVB05. Final report |
| [12] | Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of the IEEE International Conference on Neural Networks IV, IEEE Service Center, Piscataway, NJ; 1995. p. 1942–1948 |
| [13] | Mehrabian A, Lucas C. A novel numerical optimization algorithm inspired from weed colonization. Ecological Informatics 2006; 355-366 |
| [14] | Balci H, Valenzuela J. Scheduling electric power generators using particle swarm optimization combined with the Lagrangian relaxation method. International Journal of Applied Math Computation 2004; 14 (3): 411–421 |
| [15] | Abido M. Optimal power flow using particle swarm optimization. Electric Power and Energy Systems 2002; 24 (7): 563–571 |
| [16] | Ahmet D, Yucekaya, Valenzuela J, Dozier G. Strategic bidding in electricity markets using particle swarm optimization. Electric Power Systems Research 2009; 79: 335–345 |
| [17] | Sahraei-Ardakani M, Roshanaei M, Rahimi Kian A, Lucas C. A Study of Electricity Market Dynamics Using Invasive Weed Colonization Optimization. In: Proceedings of the IEEE Symposium on Computational Intelligence and Games. Perth, Austoralia: 2009, 276-282 |

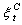 The non-discounted price tariff in period t [Rial/KWh] (t=1 is the off-peak, t=2 is the normal, and t=3 is the peak period).
The non-discounted price tariff in period t [Rial/KWh] (t=1 is the off-peak, t=2 is the normal, and t=3 is the peak period).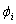 The outage cost of the ith customer [Rial/KWh].
The outage cost of the ith customer [Rial/KWh].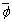 The maximum outage cost.
The maximum outage cost.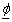 The minimum outage cost.
The minimum outage cost.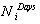 The number of days that customer-i receives discount in its price tariff.
The number of days that customer-i receives discount in its price tariff.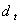 The duration of period t [hours].
The duration of period t [hours].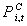 The normal power consumption of customer-i in period t [KW].
The normal power consumption of customer-i in period t [KW].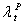 The market clearing price of electric energy (MCP) in period t [Rial/KWh].
The market clearing price of electric energy (MCP) in period t [Rial/KWh].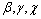 Coefficients of generation cost function.
Coefficients of generation cost function.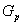 Amount of power generated by generation units.A positive value added to market clearing price to determine non-discounted tariff.Decision variables:
Amount of power generated by generation units.A positive value added to market clearing price to determine non-discounted tariff.Decision variables: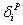 The amount of load interruption for customer-i [kW].
The amount of load interruption for customer-i [kW]. 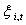 The customer-i discounted price tariff (as a reward for participating in the DMP) in period t [Rial/kWh].
The customer-i discounted price tariff (as a reward for participating in the DMP) in period t [Rial/kWh].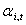 The discount factor for customer-i (in its price tariff) for period t.
The discount factor for customer-i (in its price tariff) for period t. 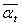 Maximum discount coefficient in period t.
Maximum discount coefficient in period t.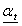 Minimum discount coefficient in period t.As mentioned before, the generation cost function is quadratic like Eq. (2.1):
Minimum discount coefficient in period t.As mentioned before, the generation cost function is quadratic like Eq. (2.1):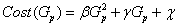
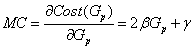
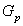 is the amount of power, and
is the amount of power, and 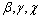 are coefficients which defined by generator units.The market clearing price,
are coefficients which defined by generator units.The market clearing price, 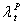 , is the point of intersection between marginal cost line and total amount of quantity demanded by customers,
, is the point of intersection between marginal cost line and total amount of quantity demanded by customers, 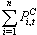 , as is shown in Figure. 1.
, as is shown in Figure. 1.
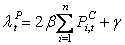
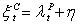
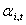 and the interruption cost
and the interruption cost 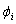 is assumed to be linear as shown in Figure. 2 and Eq. (2.5).
is assumed to be linear as shown in Figure. 2 and Eq. (2.5). 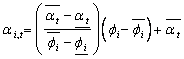

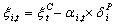
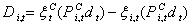
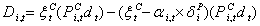
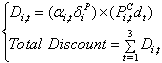
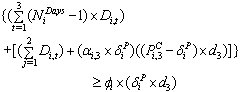
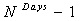 ) days even though the customer’s load is not curtailed; in the second part, the customer’s load is curtailed during the peak hours. The Ndays variable is set during the optimization process such that inequality (2.10) is satisfied. If one converts the inequality (2.10) into an equality constraint, then the Ndays variable could be analytically computed as follows:
) days even though the customer’s load is not curtailed; in the second part, the customer’s load is curtailed during the peak hours. The Ndays variable is set during the optimization process such that inequality (2.10) is satisfied. If one converts the inequality (2.10) into an equality constraint, then the Ndays variable could be analytically computed as follows: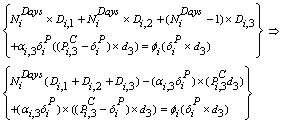
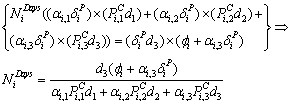
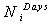 is a function of other parameters and decision variables.The objective function of the power utility is to maximize the total profit from selling power to its n customers as shown in equation (2.13),
is a function of other parameters and decision variables.The objective function of the power utility is to maximize the total profit from selling power to its n customers as shown in equation (2.13), 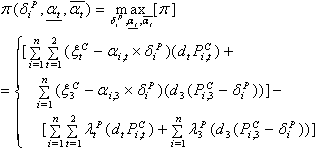
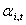 is a function of
is a function of 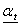 and
and 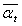 , the utility’s profit will be a function of
, the utility’s profit will be a function of 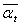 ,
, 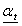 and
and 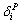 .The objective of the power utility is to maximize its total profit with respect to the following constraints:
.The objective of the power utility is to maximize its total profit with respect to the following constraints: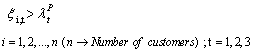
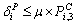
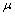 is the limiting load curtailment percentage.
is the limiting load curtailment percentage.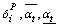 for each customer of a PU. The PSO is an extremely simple search method that seems to be very effective for optimizing a wide range of problems related to power systems[14,15,16]. The IWO is a stochastic numerical algorithm inspired from weed colonization. The IWO has shown successful results in many practical applications like optimization and analysis of electricity markets dynamics[17]. As the purpose of this paper is not to discuss about the details of these two algorithms, here only the parameters of these two algorithms are defined. For more information about the details of these algorithms see[12,13]. The chosen parameters for both the PSO and IWO algorithms are given in Tables 1 and 2. These parameters are selected according to[12], and[13], respectively.
for each customer of a PU. The PSO is an extremely simple search method that seems to be very effective for optimizing a wide range of problems related to power systems[14,15,16]. The IWO is a stochastic numerical algorithm inspired from weed colonization. The IWO has shown successful results in many practical applications like optimization and analysis of electricity markets dynamics[17]. As the purpose of this paper is not to discuss about the details of these two algorithms, here only the parameters of these two algorithms are defined. For more information about the details of these algorithms see[12,13]. The chosen parameters for both the PSO and IWO algorithms are given in Tables 1 and 2. These parameters are selected according to[12], and[13], respectively.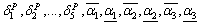 ).The
).The 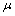 coefficient in (2.15) is set to 0.2, which means that the PU may interrupt up to a maximum of 20% of each customer’s load. The
coefficient in (2.15) is set to 0.2, which means that the PU may interrupt up to a maximum of 20% of each customer’s load. The 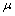 in (2.4) is set to 100 Rials, which means that non-discounted tariff is 100 Rials more than market clearing price. By evaluating the situation and data for this case study
in (2.4) is set to 100 Rials, which means that non-discounted tariff is 100 Rials more than market clearing price. By evaluating the situation and data for this case study 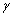 is set to 12 for all three periods.
is set to 12 for all three periods. 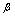 is set to 0.124, 0.0135, and 0.0275 for off-peak, normal, and peak periods respectively. The five customers’ loads during the peak, normal, and off-peak hours are given in Table 3 and Figure. 3.
is set to 0.124, 0.0135, and 0.0275 for off-peak, normal, and peak periods respectively. The five customers’ loads during the peak, normal, and off-peak hours are given in Table 3 and Figure. 3.
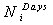 is computed for each customer and if its value was non-integer then it will be rounded up to the closest integer.The optimal electricity price tariffs are also given in Table 6. The discounted price tariffs are higher than the market price of electricity to ensure the positive profit for the PU.Table 7 shows the discount coefficients for 5 customers. These discount factors are related to the outage costs, meaning that the discount factors for the customers with higher outage costs are higher than those for the customers with lower outage costs (assuming that all of them participate in the DMP by the PU). To illustrate the cost of electricity for each customer, Figure. 4 to Figure 6 show these costs before and after participating in the demand management program. These figures show the average cost in
is computed for each customer and if its value was non-integer then it will be rounded up to the closest integer.The optimal electricity price tariffs are also given in Table 6. The discounted price tariffs are higher than the market price of electricity to ensure the positive profit for the PU.Table 7 shows the discount coefficients for 5 customers. These discount factors are related to the outage costs, meaning that the discount factors for the customers with higher outage costs are higher than those for the customers with lower outage costs (assuming that all of them participate in the DMP by the PU). To illustrate the cost of electricity for each customer, Figure. 4 to Figure 6 show these costs before and after participating in the demand management program. These figures show the average cost in 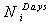 for each customer in three demand periods. As shown in these figures, the cost of electricity for each customer gets lower by participating in the DMP and therefore their outage costs are compensated.
for each customer in three demand periods. As shown in these figures, the cost of electricity for each customer gets lower by participating in the DMP and therefore their outage costs are compensated.


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML