Rubayat Hasan , Ariful Islam , Raton Kumar Nondy
Department of Electrical and Electronics Engineering, International University of Business Agriculture and Technology, Dhaka, Bangladesh
Correspondence to: Rubayat Hasan , Department of Electrical and Electronics Engineering, International University of Business Agriculture and Technology, Dhaka, Bangladesh.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper a new approach to adaptive stabilization using Minimal Control Synthesis (MCS) algorithm for a synchronous power system is proposed. The MCS algorithm is a significant extension of hyperstability based model reference adaptive control approach. The main feature of the algorithm is that it requires simple structure and a few computational requirements to implement the strategy. The controller uses the proportional plus integral type adaptation mechanism to satisfy the hyperstability conditions for taking care of plant parameter changes, small disturbances and plant nonlinearities. The stabilization signals are synthesized at the excitation input of the machine system such that a well defined closed-loop performance is achieved. The proposed adaptive control scheme avoids the difficulty of satisfying the Kalman-Yakubovich Lemma, model matching condition and the complexity of implementing an online parameter estimator. Above all, the hyperstability guarantees asymptotical stability of the power system under a disturbance. The power system under investigation consists of a synchronous machine connected to an infinite bus. It has both voltage regulator and speed governor controls. The effectiveness of the controller for damping machine oscillations caused by power system disturbances is verified by simulation studies.
Keywords:
Power system, Dynamic Stability, Hyperstability, Lyapunov equation
Cite this paper: Rubayat Hasan , Ariful Islam , Raton Kumar Nondy , An Adaptive Controller Based on Minimal Control Synthesis Algorithm for a Single Machine Infinite Bus Power System, Electrical and Electronic Engineering, Vol. 10 No. 1, 2020, pp. 1-6. doi: 10.5923/j.eee.20201001.01.
1. Introduction
The power system behaves essentially as a set of coupled oscillators which are continuously perturbed due to load fluctuations and parameter changes. The amortisseur or damper effects can suppress the higher frequency oscillations. But the lower frequency oscillations are insensitive to damper windings and dynamic instabilities are associated with these lower frequency modes. Oscillations of small magnitude and low frequency in the range 0.5 Hz to 2.5 Hz often persist for a longer period of time and limit the transmission of power [1],. It is also assumed that the voltage regulator introduces negative damping at increased load [1],. The increasingly challenging dynamic electric power system problems however are not hopelessly unmanageable. The challenging new problems are always met by new ideas and new methods aimed in solving the problems. To improve system damping, in general, artificial means of producing torques in phase with the speed are introduced by Supplementary Stabilizing Signals (SSSs) designed by supplementary excitation controls. The network used to generate SSSs during low frequency oscillations is Power System Stabilizer (PSS) [2]. A major concern of power system engineers is to keep the power system under control at all times. PSSs have been widely used to enhance the system damping and to improve the dynamic stability of power systems for many years [3], [4], [1], [5-9]. Power systems are generally nonlinear and highly dynamical systems. The linearized model of the power system is used with linear optimal control theory to design the fixed parameter conventional PSS. The optimal controllers are reported to be very effective for damping machine oscillations [1]. But when the operating condition changes under a disturbance, the fixed parameter controllers cannot maintain the power system dynamical stability. Thus the parameters of these controllers must be re-tuned so that they can provide the desired performances. The additional damping signal is introduced through the excitation system by the extra damping torque modulation. Thus to improve the dynamic characteristics of the system over a wide range of operating points, adaptive controls have been proposed [5], [10], [11].Two main approaches to adaptive control have been reported by power system engineers: Self Tuning Adaptive Control (STAC) and Model Reference Adaptive Control (MRAC) [12].In the STAC scheme, parameter identification techniques, such as the recursive least squares method, is used to identify system parameters online and these parameter estimates are then incorporated in the control policy. In the MRAC scheme, a reference model exhibiting the desired system response is included in the control strategy. The error between the output of the actual system and that of the reference model is used to update the controller parameters with the objective of the system output converging to the model output. Although adaptive PSSs based on STAC or MRAC have been reported to be effective, the inherent assumptions and the nonlinearities associated with the adaptive controllers raise a number of basic questions whose actual answers may bring complexity to the control structure. The parameter estimator design in STAC and the appropriate selection of the reference model in MRAC often meet with difficulties in practical implementation. It is reported that the MCS algorithm based on hyperstability theory of Popov can be retro-fitted to an existing control strategy and closed-loop robustness will be greatly enhanced. The MCS algorithm has already been successfully applied to Multi-machine power systems with decentralized control strategy to damp machine oscillations [13]. The adaptive controller in power systems is often used as a supplementary controller in conjunction with a conventional fixed parameter controller. While the conventional controllers regulate the normal voltage and frequency adjustments, the supplementary adaptive controller is used to improve the dynamical stability as restoring the system to normal operating conditions after suffering a disturbance. A new design approach based on the MCS algorithm for the supplementary adaptive PSS is proposed herein for a higher order power system. A numerical example of a Single Machine Infinite Bus (SMIB) power system with control equipment has been studied to verify the efficacy of this approach. The simulation results show that the adaptive controller based on MCS algorithm works well under system parameter variations and with different small disturbances.
2. Power System Dynamic Problem
There are various kinds of power system dynamic problems such as high or low frequency oscillations, large or small disturbances. However, there are only a limited number of system components important to the dynamic study: the hydraulic and steam turbines, the synchronous generator, the governor and the excitation system. The three phase synchronous generator used for large scale electric power generation has two synchronously rotating fields, one dc-excited field on the rotor with a field winding mechanically rotated normally at the synchronous speed. The other ac-excited field on the stator with the three phase stator winding, each phase winding is 120° apart from the others electrically, and each phase current with a 120° time phase difference with respect to others. The speed of the three phase ac field on the stator is completely dictated by the system frequency and the field appears in and around the air gap of the machine instantly because of the nature of the electro- magnetic field. The speed and hence the dc field of the rotor are affected by the inertia and damping of the rotating system. Only in the steady state, when the mechanical energy input and the electric energy output plus the system losses are in complete balance, will there be neither acceleration nor deceleration of the rotating system. In such a case, the two rotating fields, one dc and one ac, will be moving together synchronously, with the N-pole of the ac field facing the S-pole of the dc field and the S-pole of the ac field facing the N-pole of the dc field across the air gap of the machine. When a disturbance occurs to the system, that input output energy balance is upset. As a result, the N to S and S to N pole bonds will be shaken causing stability problems.
3. Problem Formulation
The usual mathematical model of a power system for stability studies enables the nonlinear power system to be written in the affine form.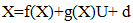 | (1) |
Where f and g are smooth vector fields. Linearzing equation (1) around an acceptable operating point gives the state space equation: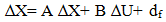 | (2) |
Where ∆ X € Rn is the change of the system state, ∆U € Rm is the change of control and df represents a vector aggregate of unknown disturbances applied to the plant. Any unmodelled terms, non-linearity’s, parameter variations and external disturbances are included in the disturbance vector df. The pair {A, B} is constant. For conciseness, (2) Will be written hereafter simply as: 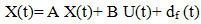 | (3) |
The reference model that defines the required state trajectory Xm is: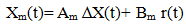 | (4) |
The reference model parameters {Am, Bm} are determined in order to elicit a well defined closed loop performance in the sense of power system stability. The main purpose of Am is to let the power system be stable and thus to influence the controlled plant such that its dynamic characteristics can be improved. A common choice of MRAC signal is given by an Extension of the state feedback tracking control strategy.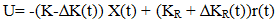 | (5) |
Where K and KR are constant feedback and feed forward gain matrices. The ∆K and ∆KR(t) terms are adaptive changes to these gains that usually results from the effects of disturbances. on the state trajectory, X. In that context ∆ does not necessarily imply ‘small’. So we shall drop ∆.The closed form solution of K and KR are: K= B+(A-Am) and KR= B+Bm where B+ is the pseuu- inverse of B. The error dynamics of the closed loop system (2) and (4) are given by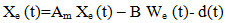 | (6) |
Where We (t)= K(t) X + KR(t) r . This assumes that the reference model (4) satisfies Erzberzer’s model matching conditions: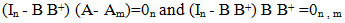 The error equation (6) can be considered as a feedback system in its own right. One writes the error signal as:
The error equation (6) can be considered as a feedback system in its own right. One writes the error signal as: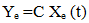 | (7) |
So that the triple {Am , Bm , C} forms a hyper stable linear block. The hyper stability condition is guaranteed if the transfer function G(s) = C(SI-A)-1B is Strictly Positive Real (SPR). That is The Kalman – Yakubovitch Lemma: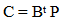 | (8) |
Where P is a Positive Definite Symmetric Matrix (PDSM) which is the solution of the Lyapunov's equation: 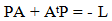 | (9) |
For PDSM characterization of P matrix and ease of computation L can be chosen as L = I where I is an identity matrix of appropriate size. Then the error Xe approaches a stable equilibrium if Popov’s Integral Inequality Condition (PIIC) is satisfied for the nonlinear block.If these conditions are satisfied then {A, B, C} is a hyper stable block and the transfer function is SPR. As the transfer function is SPR the anti-wind up problem is also solved [14]. Further, SPR function can tolerate large uncertainties, external disturbances and nonlinearities. This explains the importance of testing positive realness of transfer function. The MCS algorithm also relaxes positivity condition of the feed forward block normally imposed by MRAC since the PDSM C in equation (9) always exists. The error ∆X tends to stable equilibrium if the Popov Integral Inequality Condition (PIIC) of the nonlinear time varying blocks: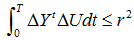 | (10) |
Where 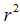 is a positive number independent of time t. The more general adaptive mechanisms are developed by Landau [11]. Based upon the hyperstability theory of Popov [15]. These adaptive mechanisms have been tested in simulation and implementation studies and have been shown to be robust in the face of external disturbances and plant parameter variations. The specific but non unique solution for the proportional plus integral type gain changes, satisfying the PIIC are:
is a positive number independent of time t. The more general adaptive mechanisms are developed by Landau [11]. Based upon the hyperstability theory of Popov [15]. These adaptive mechanisms have been tested in simulation and implementation studies and have been shown to be robust in the face of external disturbances and plant parameter variations. The specific but non unique solution for the proportional plus integral type gain changes, satisfying the PIIC are: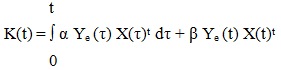 | (11) |
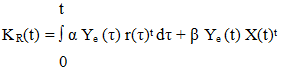 | (12) |
Where α and β are adaptive weights which are chosen empirically.
4. Proposed Adaptive MCS Control Scheme
The desired adaptive control approach to the above MRAC formulation assumes that K=0m,n and KR = 0m and then (5) becomes: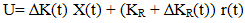 | (13) |
Whilst (8) is written as [8]: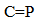 | (14) |
where P is the solution of the Liapunov equation (9). 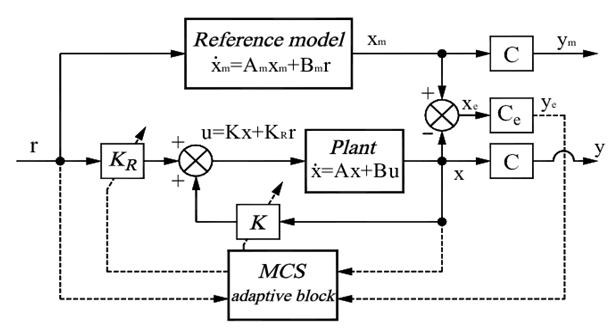 | Figure 1. Proposed Adaptive Control Scheme |
5. The Design Procedure
It involves the following process-(i) Development of a state space model for the power system.(ii) A stable matrix Am is always chosen. The main purpose of Am is to let the power system be stable and thus to influence the controlled plant such that the stabilization characteristics can be improved.In this paper the reference model is chosen by using strip eigenvalue assignment technique with a specified damping ratio [9].
6. System Studied
The design methodology proposed in this paper is applied to a single-machine infinite bus power system with control equipment such as speed governor and voltage regulator [8].The state vector is: 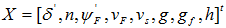 | (15) |
Where state variables are: torque angle 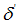 , speed
, speed 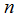 , field flux linkage
, field flux linkage 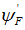 , field voltage
, field voltage 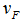 , feedback voltage
, feedback voltage 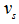 , gate opening
, gate opening 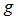 , governor feedback loop signal
, governor feedback loop signal 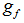 , and water head
, and water head 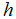 .
.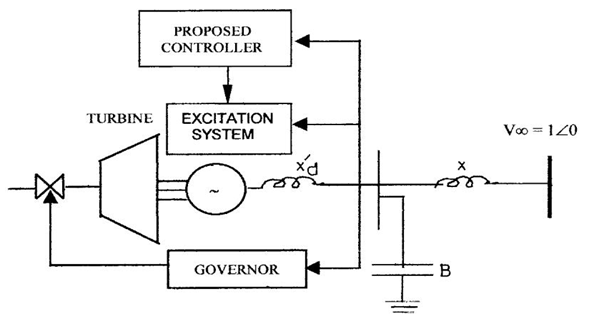 | Figure 2. Single Machine Infinite Bus Power System [8] |
7. Selection of Reference Model
For normal operating condition, {P0 , Q0} as {0.735, 0.034}, the eigenvalues of the uncontrolled system  (A)=[−0.0105 ± j 0.7947, −0.1969, −0.0572, −0.0672 ± j 0.1947, −0.2740, −13.70].The first pair of complex conjugate eigenvalues with negative real part related to rotor oscillations is known as the Electro Mechanical (EM) mode. The damping ratio of this mode is 0.0132, which is very low because it is not lying within the acceptable range 0.1 to 0.5 [9].
(A)=[−0.0105 ± j 0.7947, −0.1969, −0.0572, −0.0672 ± j 0.1947, −0.2740, −13.70].The first pair of complex conjugate eigenvalues with negative real part related to rotor oscillations is known as the Electro Mechanical (EM) mode. The damping ratio of this mode is 0.0132, which is very low because it is not lying within the acceptable range 0.1 to 0.5 [9].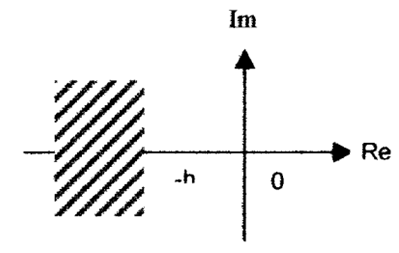 | Figure 3. Strip eigenvalues h > 0 |
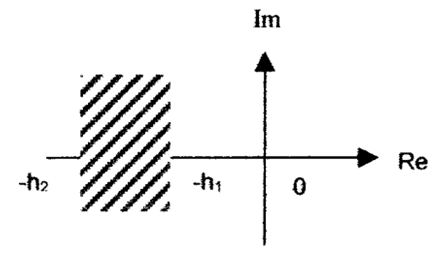 | Figure 4. Strip eigenvalues in vertical strip |
To find the stable reference model by the SEA technique [9] one selects the strip {−h1, −h2} as {−0.05, −0.45}.The stable matrix obtained is: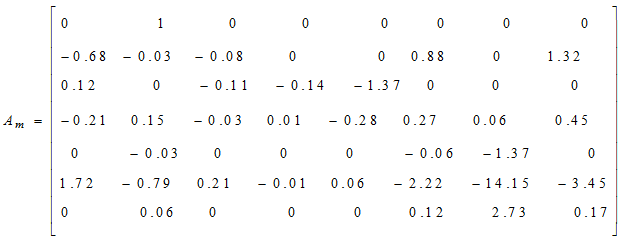 The eigenvalues of this reference matrix are:
The eigenvalues of this reference matrix are: (Am)= [-0.25 ± j0.7770, -0.1969, -0.0572, -0.0672 ± j0.1947, -0.2740,-13.70]. The damping ratio of the EM is 0.3451 which is well within the acceptable range 0.1 to 0.5. A number of stable reference models are obtained but only the model for nominal operating point is presented. It is mentioned that for each possible operating condition, the damping ratio lies within the acceptable range 0.1 to 0.5.
(Am)= [-0.25 ± j0.7770, -0.1969, -0.0572, -0.0672 ± j0.1947, -0.2740,-13.70]. The damping ratio of the EM is 0.3451 which is well within the acceptable range 0.1 to 0.5. A number of stable reference models are obtained but only the model for nominal operating point is presented. It is mentioned that for each possible operating condition, the damping ratio lies within the acceptable range 0.1 to 0.5.
8. Zero Order Hold Discrete Equation of MCS Algorithm
The implemented discrete time form of the MCS algorithm can be taken from the Zero Order Hold Discrete Equations (ZOHDEs),Xm(k+1)= (In + T Am ) Xm (k) + Bm r (k)Xe (k) = Xm (k) - X(k)K (k) = K (k-1) + β Ye (k) X (k)t - µYe (k-1) X (k-1)KR (k) = KR (k-1) + β Ye (k) r (k)t - µYe (k-1) r (k-1)U(k)= K (k) ) X (k) + KR (k) r (k)Ye (k) = Ce Xe (k) Where, K (-1) = 0m,n ; KR(-1) = 0m andµ=β- α T. Here T is the sampling interval of the discrete time process.
9. Simulation Result
Under the normal operating condition, a small signal disturbance X = [0, .02, 0, 0, 0, 0, 0, 0]t is applied to the system and it is found from Figure 5 (a) that the proposed controller damps out the low frequency oscillations very quickly. The system is simulated for 30% change of inertia M and the responses are shown in Figure 5(b). It is seen that, in all cases the uncontrolled system is highly oscillatory. Thus the controller works well in the face of parameter changes and the results demonstrate the effectiveness of the proposed adaptive controller.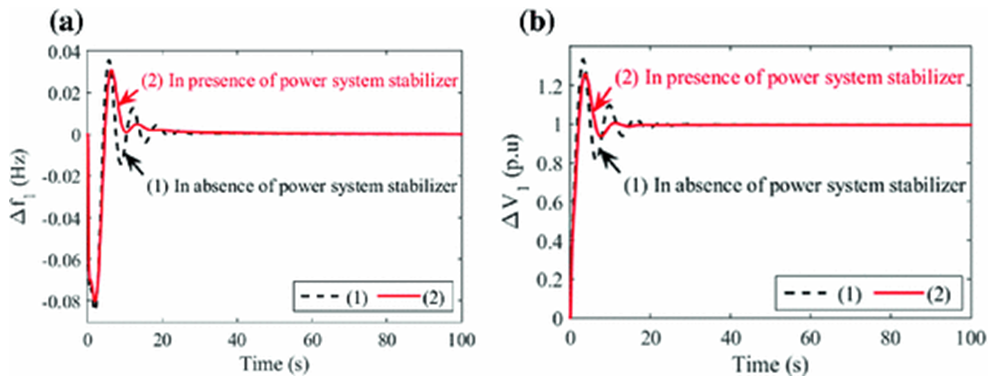 | Figure 5. Responses of the System with the proposed MCS |
Next, it is possible to change the electromagnetic parameters of the generator by changing the rotor angle and by mounting additional flywheel on the shaft of the model generator, as well as by connecting additional reactance at the generator terminal.
10. Conclusions
An adaptive controller based on the MCS algorithm has been developed for a SMIB power system. The design method is simple and it avoids the massive amount of calculations and computations. The control is constructed so that the closed loop system is asymptotically hyper stable, which guarantees the dynamical stability improvement of the power system. Two separate changeable gains act as the adaptive mechanisms. For the power system investigated MCS algorithm relaxes positivity condition of the feed forward block normally imposed by MRAC since the positive definite matrix P always exists. Simulation result shows that the proposed controller works well under the face of parameter changes or disturbances. Hyperstability has nice links with the passivity so the proposed method can be applied to large scale interconnected power systems using the concept of system passivity.
References
| [1] | Y.-n. Yu, et al., "Application of an optimal control theory to a power system," IEEE Transactions on Power Apparatus and Systems, pp. 55-62, 1970. |
| [2] | P. M. Anderson and A. A. Fouad, "Power system control and stability, Vol. 1," IOWA State University press, Ames, IOWA, USA, 1977. |
| [3] | Y. Mitani, et al., "Application of superconducting magnet energy storage to improve power system dynamic performance," IEEE Transactions on Power Systems, vol. 3, pp. 1418-1425, 1988. |
| [4] | Y.-Y. Hong and W.-C. Wu, "A new approach using optimization for tuning parameters of power system stabilizers," IEEE Transactions on Energy Conversion, vol. 14, pp. 780-786, 1999. |
| [5] | D. A. Pierre, "A perspective on adaptive control of power systems," IEEE Transactions on Power Systems, vol. 2, pp. 387-395, 1987. |
| [6] | Y. Song, "Novel adaptive control scheme for improving power system stability," in IEE Proceedings C (Generation, Transmission and Distribution), 1992, pp. 423-426. |
| [7] | F. P. Demello and C. Concordia, "Concepts of synchronous machine stability as affected by excitation control," IEEE Transactions on Power Apparatus and Systems, vol. 88, pp. 316-329, 1969. |
| [8] | P. D. Nondy, RK, "An Adaptive controller for improving dynamic stability of synchronous power system," Electric Machines &Power Systems, vol. 28, pp. 1-11, 2000. |
| [9] | Y.-C. Lee and C.-J. Wu, "Damping of power system oscillations with output feedback and strip eigenvalue assignment," IEEE Transactions on Power Systems, vol. 10, pp. 1620-1626, 1995. |
| [10] | A. Ghosh, et al., "Power system stabilizer based on adaptive control techniques," IEEE Transactions on Power Apparatus and Systems, pp. 1983-1989, 1984. |
| [11] | S. Qu and C. Chen, "Low frequency oscillations damping by STATCOM with a fuzzy supplementary controller," in Proceedings. International Conference on Power System Technology, 2002, pp. 67-70. |
| [12] | X. Dai and Q. Chao, "The research of photovoltaic grid-connected inverter based on adaptive current hysteresis band control scheme," in 2009 International Conference on Sustainable Power Generation and Supply, 2009, pp. 1-8. |
| [13] | P. Doraraju and R. Nondy, "A decentralized adaptive stabilizer based on minimal control synthesis algorithm for a multi-machine power system," in Proceedings of IEEE International Conference on Industrial Technology 2000 (IEEE Cat. No. 00TH8482), 2000, pp. 307-312. |
| [14] | D. Stoten and S. Hodgson, "Comparative implementation studies of the minimal control synthesis algorithm on a class 1 manipulator," Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, vol. 205, pp. 23-33, 1991. |
| [15] | G. Tao, "A simple alternative to the Barbalat lemma," IEEE Transactions on Automatic Control, vol. 42, p. 698, 1997. |


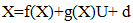
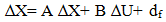
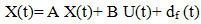
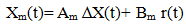
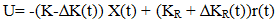
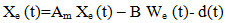
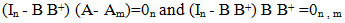 The error equation (6) can be considered as a feedback system in its own right. One writes the error signal as:
The error equation (6) can be considered as a feedback system in its own right. One writes the error signal as: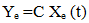
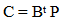
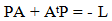
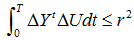
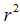 is a positive number independent of time t. The more general adaptive mechanisms are developed by Landau [11]. Based upon the hyperstability theory of Popov [15]. These adaptive mechanisms have been tested in simulation and implementation studies and have been shown to be robust in the face of external disturbances and plant parameter variations. The specific but non unique solution for the proportional plus integral type gain changes, satisfying the PIIC are:
is a positive number independent of time t. The more general adaptive mechanisms are developed by Landau [11]. Based upon the hyperstability theory of Popov [15]. These adaptive mechanisms have been tested in simulation and implementation studies and have been shown to be robust in the face of external disturbances and plant parameter variations. The specific but non unique solution for the proportional plus integral type gain changes, satisfying the PIIC are: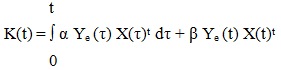
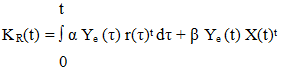
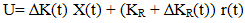

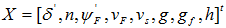
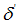 , speed
, speed 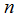 , field flux linkage
, field flux linkage 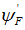 , field voltage
, field voltage 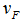 , feedback voltage
, feedback voltage 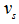 , gate opening
, gate opening 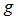 , governor feedback loop signal
, governor feedback loop signal 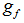 , and water head
, and water head 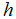 .
.
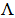 (A)=[−0.0105 ± j 0.7947, −0.1969, −0.0572, −0.0672 ± j 0.1947, −0.2740, −13.70].The first pair of complex conjugate eigenvalues with negative real part related to rotor oscillations is known as the Electro Mechanical (EM) mode. The damping ratio of this mode is 0.0132, which is very low because it is not lying within the acceptable range 0.1 to 0.5 [9].
(A)=[−0.0105 ± j 0.7947, −0.1969, −0.0572, −0.0672 ± j 0.1947, −0.2740, −13.70].The first pair of complex conjugate eigenvalues with negative real part related to rotor oscillations is known as the Electro Mechanical (EM) mode. The damping ratio of this mode is 0.0132, which is very low because it is not lying within the acceptable range 0.1 to 0.5 [9].

 The eigenvalues of this reference matrix are:
The eigenvalues of this reference matrix are: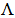 (Am)= [-0.25 ± j0.7770, -0.1969, -0.0572, -0.0672 ± j0.1947, -0.2740,-13.70]. The damping ratio of the EM is 0.3451 which is well within the acceptable range 0.1 to 0.5. A number of stable reference models are obtained but only the model for nominal operating point is presented. It is mentioned that for each possible operating condition, the damping ratio lies within the acceptable range 0.1 to 0.5.
(Am)= [-0.25 ± j0.7770, -0.1969, -0.0572, -0.0672 ± j0.1947, -0.2740,-13.70]. The damping ratio of the EM is 0.3451 which is well within the acceptable range 0.1 to 0.5. A number of stable reference models are obtained but only the model for nominal operating point is presented. It is mentioned that for each possible operating condition, the damping ratio lies within the acceptable range 0.1 to 0.5.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML