Md. Mashiur Rahman1, A. H. M. Zadidul Karim2
1Compentence Domain Radio Access Network, Ericsson Telecommunications Pte Ltd, Singapore
2Department of EEE, University of Asia pacific, Dhaka, Bangladesh
Correspondence to: Md. Mashiur Rahman, Compentence Domain Radio Access Network, Ericsson Telecommunications Pte Ltd, Singapore.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Image Registration is the process of estimating an optimal transformation between two images. There are many application of image registration now a day such as in FMRI motion correction, geometric distortion in EPI, alignment of images obtained at different time or with imaging parameters, formation of composite functional maps, mapping of PET/SPECT to MRI image. In this work the image registration analysis is done using the affine transformation model in our proposed three method image registration using ‘pixel’, ‘wavelet’ and ‘translation’ method. A comparative experiment in between these methods based on the analysis time and root mean square deviation. If the image is displaced from its place which means it can be rotated, displaced from its original axis vertically or horizontally this method can detect the displacement and can get the original image. At first we do a random rotation and then we find an image which is larger in size from the original image. Then we again rotate the image by reshaping the size of the image. The registered is finding from again rotating the image in a loop and tries to find a relation between them. From this relation we get the value at which the image was rotated or displaced from the original image. Then we reverse the process and get the final result.
Keywords:
Pixel method, Wavelet method, Translation method
Cite this paper: Md. Mashiur Rahman, A. H. M. Zadidul Karim, Comparative Analysis of Image Registration Using Pixel, Wavelet and Translation Method, Electrical and Electronic Engineering, Vol. 5 No. 2, 2015, pp. 23-33. doi: 10.5923/j.eee.20150502.01.
1. Introduction
Image registration is one of the most important tasks in image processing. Image registration is the process of overlaying two or more images of the same scene taken at different times, from different viewpoints or by different sensors. It geometrically aligns two images—the reference and sensed images. The present differences between images are introduced due to different imaging conditions. Image registration is a crucial step in all image analysis tasks in which the final information is gained from the combination of various data sources like in image fusion, change detection, and multichannel image restoration. Typically, registration is required in remote sensing (multispectral classification, environmental monitoring, change detection, image moseying, and weather forecasting, creating super-resolution images, integrating information into geographic information systems (GIS)), in medicine (combining computer tomography (CT) and NMR data to obtain more complete information about the patient, monitoring tumor growth, treatment verification, comparison of the patient’s data with anatomical atlases).It has many potential applications in clinical diagnosis (Diagnosis of cardiac, retinal, pelvic, renal, abdomen, liver, tissue etc. disorders). It is a process of aligning two images into a common coordinate system thus aligning them in order to monitor subtle changes between the two. Registration algorithms compute transformations to set correspondence between the two images the purpose of this paper is to provide a comprehensive review of the existing literature available on Image registration methods. We believe that it will be a useful document for researchers longing to implement alternative Image registration methods for specific applications.With the development of computer technology, medical imaging technology has been widely used in clinical diagnosis and medical treatment; there are a variety of image modes because of the different image principles and devices. In order to better analysis the disease condition of patients, doctors can get a comprehensive organ or diseased image by repeating image of multi-modality or the same pattern and fusing of these images, hence they make an accurate diagnosis. The fused image must be registered. Image registration is finding a space change which can make it reach space agreement to the corresponding points of another one or the other images. Medical image registration is a hot bio-medical engineering issue and a difficult issue. In recent years many scholars made a number of new registration methods, such as co-correlation, Fourier, point map and MI. The more effective method is MI. Because it doesn't require image segmentation, feature extraction and other image pre-processing, and it possesses sub-pixel level, strong adaptability and high automation, snidely applied in the world. But the MI is calculated by the joint histogram of two images, the respective changing of gray from both images will result in greater impact to the registration result, especially to those images lacking of grayscale, the registration precision will be degraded. In addition, the method of MI uses only information from corresponding points, and doesn’t take into account the space-position relationship of image pixels, but in the actual registration problems, two-dimensional information of images (such as contour and edge) often plays a vital role. Therefore, using MI alone will result in mismatching easily. Some scholars have proposed many modified ways which combine MI with image features. Image feature points has been received widespread attention because of its extraction conveniently and geometric representation simply. For example, Xuan Lv [1] proposed a registration method based on corner points and MI. Yuanlian Huo [2] gave a registration methods combination MI with feather points. However, the corner points or feature points only pay attention to partial image information in the image registration. Corner points are very flexible, so they can distribute everywhere of the image and guide registration by matching feature points. While feature points registration algorithm can quickly realizes image registration according to image edges feather points, but the ability of dealing with the region away from the contours is very weak. Both methods have their own characteristics, and we can take into account integrating them, and make use of their advantages to achieve image registration. Therefore, this paper proposes a new method based on MI of multi-scale Harris corner and feature points. Firstly, extract multi-scale Harris corner points of both images. Then use the Sobel operator and the mathematical morphology methods to extract image contour and get discrete points. Finally, find maximum MI of the corner points and feather points to achieve the image registration. Experimental results show that this algorithm is simple and has every good precision and robustness.
2. Proposed Registration Methods
Image registration is the process of aligning two or more images of the same scene. Typically, one image, called the base image or reference image, is considered the reference to which the other images, called input images, are compared. The object of image registration is to bring the input image into alignment with the base image by applying a spatial transformation to the input image. The differences between the input image and the output image might have occurred as a result of terrain relief and other changes in perspective when imaging the same scene from different viewpoints. Lens and other internal sensor distortions, or differences between sensors and sensor types, can also cause distortion. This paper describes the image registration capabilities of the Image Processing. Image registration is the process of aligning two or more images of the same scene. Image registration is often used as a preliminary step in other image processing applications. Although it is well known that cross correlation can be efficiently implemented in the transform domain, the normalized form of cross correlation preferred for feature matching applications does not have a simple frequency domain expression. Normalized cross correlation (NCCR) has been computed in the spatial domain for this reason. The correlation between two signals (cross correlation) is a standard approach to feature detection as well as a component of more sophisticated techniques. Textbook presentations of correlation describe the convolution theorem and the attendant possibility of efficiently computing correlation in the frequency domain using the fast Fourier transform. Unfortunately the normalized form of correlation (correlation coefficient) preferred in template matching does not have a correspondingly simple and efficient frequency domain expression. For this reason normalized cross-correlation has been computed in the spatial domain. Due to the computational cost of spatial domain convolution, several inexact but fast spatial domain matching methods have also been developed. This paper describes a recently introduced algorithm for obtaining normalized cross correlation (NCCR) from transform domain convolution. The new algorithm in some cases provides an order of magnitude speedup over spatial domain computation of normalized cross correlation [3].There are three types of image registration techniques we have proposed to do. All these techniques are based on the normalized cross correlation.• Image registration using pixel method.• Image registration using the wavelet decomposition method.• Image registration using the translation method.
2.1. Image Registration Using Pixel Method
Pixel means the number of dots in the image. In digital imaging, a pixel is a single point in a raster image, or the smallest addressable screen element. Each pixel has its own address. The address of a pixel corresponds to its coordinates. Pixels are normally arranged in a two-dimensional grid, and are often represented using dots or squares. Each pixel is a sample of an original image; more samples typically provide more accurate representations of the original. The intensity of each pixel is variable. In color image systems, a color is typically represented by three or four component intensities such as red, green, and blue, or cyan, magenta, yellow, and black [4].Image registration using pixel method means to change the label of intensity of pixel. We calculate the relation between the normalize cross-correlation and the angle of rotation on the basis of pixel value.
2.2. Image Registration Using Wavelet Decomposition Method
A wavelet is a wave-like oscillation with amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have specific properties that make them useful for signal processing. Wavelets can be combined, using a "shift, multiply and sum" technique called convolution, with portions of an unknown signal to extract information from the unknown signal. As a mathematical tool, wavelets can be used to extract information from many different kinds of data, audio signals and images.There are two parts in the wavelet decomposition they are the approximation coefficients and the detail coefficients. These two combines the decomposition of wavelet. Here we extract the approximation coefficient only. We calculate the approximation at label 5. In the pixel registration we also use the approximation coefficient. We see that in wave transform both the rotation and the translation can be done at a time using wavelet transformation method [5].
2.3. Image Registration Using Translation Method
Special transformation in short form known as ‘translation’. Special transformation means change in angle, change in axis, change in the scaling factor, change in shear factor along the axis, displacement along the axis. The structure is created on the basis of these parameters. All the change is happening here is the value of pixel that means the number of points in the image. ‘affine’ transform means Transformation that can include translation, rotation, scaling, and shearing. Straight lines remain straight, and parallel lines remain parallel, but rectangles might become parallelograms. We use the ‘affine’ transform in this image registration process [5, 6].
3. Algorithm
Normalized cross-correlation of the two matrices. One matrix must be larger than the other to be meaningful. The value of the matrix cannot all be the same.normxcorr2 uses the following general procedure:• Calculate cross-correlation in the spatial or the frequency domain, depending on size of images.• Calculate local sums by pre computing running sums. • Use local sums to normalize the cross-correlation to get correlation coefficients.The implementation closely follows following formula from:
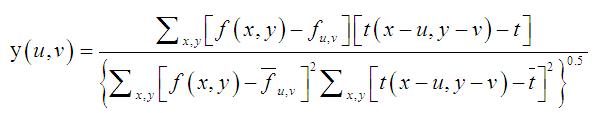 Where f is the image,
Where f is the image, 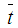 the mean of the template,
the mean of the template, 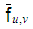 is the mean of f(x,y) in the region under the template.
is the mean of f(x,y) in the region under the template.
3.1. Block Diagram
This block diagram shows the process of these three methods. The first two methods contain almost same procedure but the third has different approach. The first one is dealing with the pixel values and the wavelet values. The wavelet contains two parts one is the approximation and another is the detail coefficient. We mainly do the analysis using approximation coefficient.
3.1.1. Image Registration Using Pixel
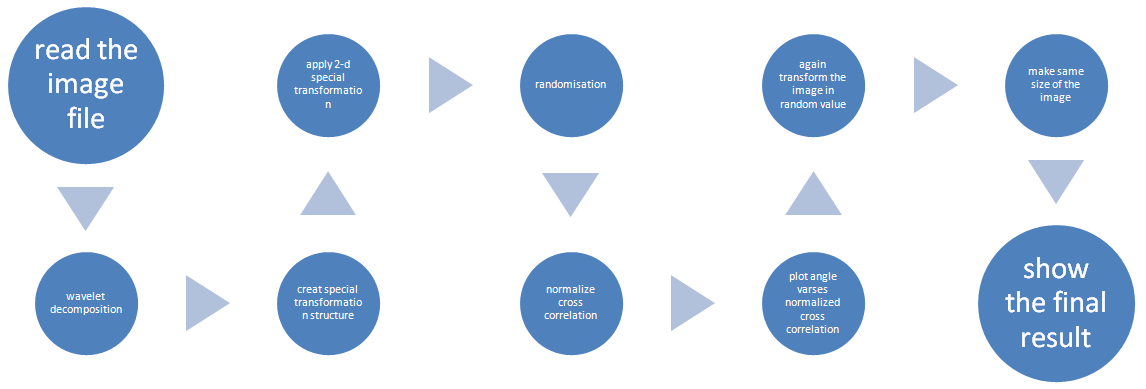 | Figure 1. Block diagram of image registration using pixel method |
3.1.2. Wavelet Decomposition Method
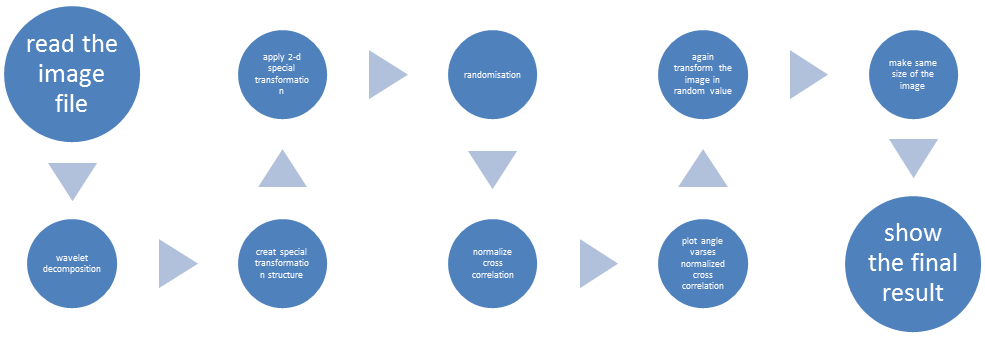 | Figure 2. Block diagram of image registration using wavelet method |
3.1.3. Translation Registration Method
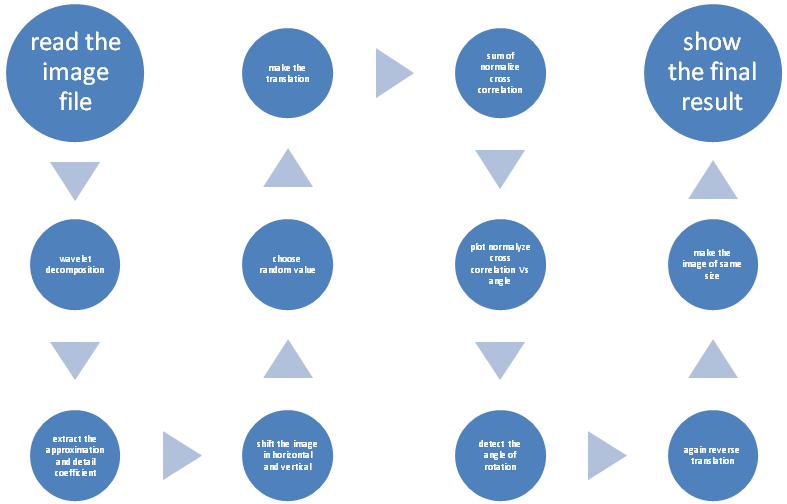 | Figure 3. Block diagram of image registration using translation method |
3.2. A Brief Description of the Block Diagram
• Read image from graphics file• Multilevel 1-D wavelet decomposition. Wavedec performs a multilevel one-dimensional wavelet • Create spatial transformation structure (TFORM). It creates a multidimensional spatial transformation structure that can be used with the function.• Apply 2-D spatial transformation to image. It transforms the image according to the 2-D spatial transformation.• Reshape the array. It returns a matrix whose elements are taken column wise.• It means round toward negative infinity. It) rounds the elements of an integer to the nearest integer.• it determines the dimensions of the array in separate variables or in specific dimension. • it determines the Normalized 2-D cross-correlation. It computes the normalized cross-correlation of the matrices template. The matrix A must be larger than the matrix template for the normalization to be meaningful. The matrix A must be larger than the matrix template for the normalization to be meaningful. • it means 3-D shaded surface plot. It views mathematical functions over a rectangular region. It creates a three-dimensional shaded surface from the component of the matrix.
4. Experimental Result
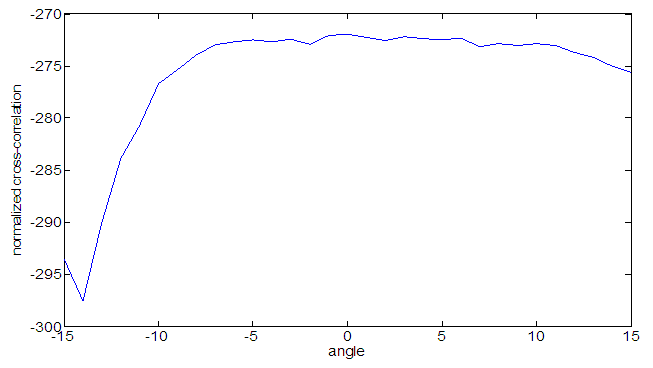
In this part we simulate all the code and get the expected result. In the case of image registration using pixel we calculate the change in pixel value on the basis of normalized cross correlation in 1 dimension analysis. We plot the angle vs. normalized cross correlation and find out the pick value in the plot and get the corresponding angle value. We use different picture and get different value for each and every one of the image. When we rotate the entire image randomly and get a random rotation value. There is some black part outside of the main picture and we need to eliminate the black part that’s why we use the crop function to eliminate the black part and get expected image.Annotation and records 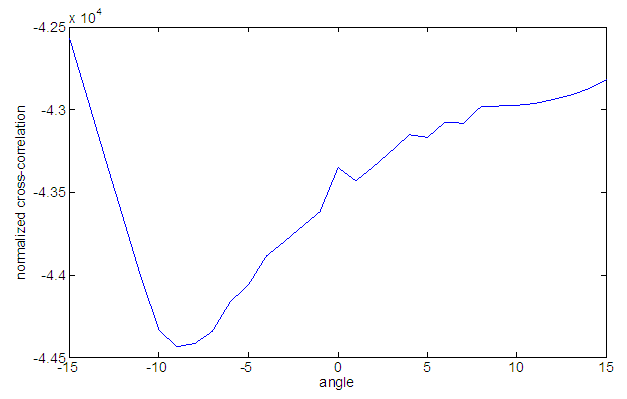 | Figure 4. Normalized cross-correlation Vs angle plot |
 | Figure 5. Final result |
(1) Image registration using wavelet decomposition method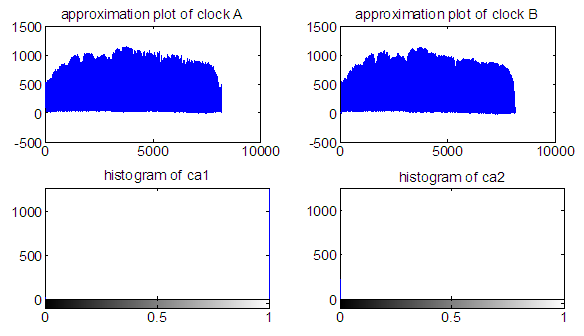 | Figure 6. Normalized cross-correlation Vs angle plot |
 | Figure 7. Normalized cross-correlation Vs angle plot |
 | Figure 8. Final result |
(2) Image registration using translation method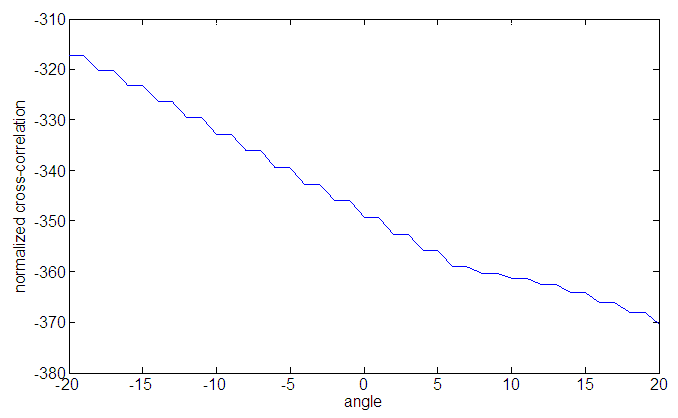 | Figure 9. Normalized cross-correlation Vs angle plot |
 | Figure 10. Final result |
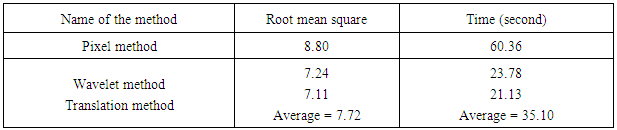
Table 1. Time and root mean square record using the same image
 |
| |
|
A. Another method in which both the rotation and the displacement along the axis occur1) Image registration using translation method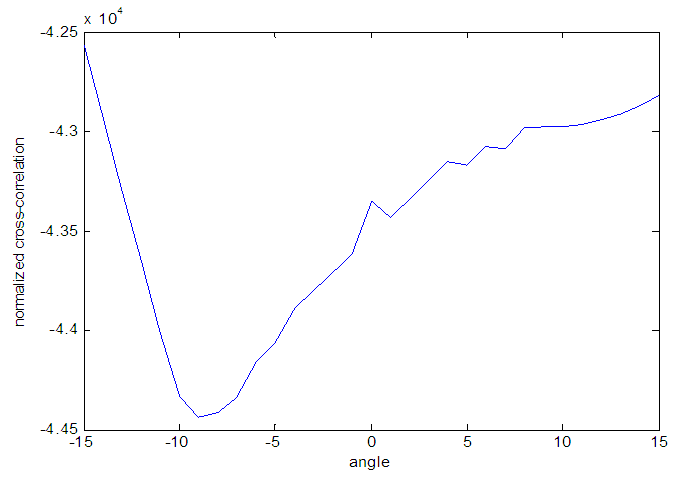 | Figure 11. Normalized cross-correlation Vs angle plot |
 | Figure 8. Final result |
2) Image registration using wavelet transformation method in case of both rotation and translation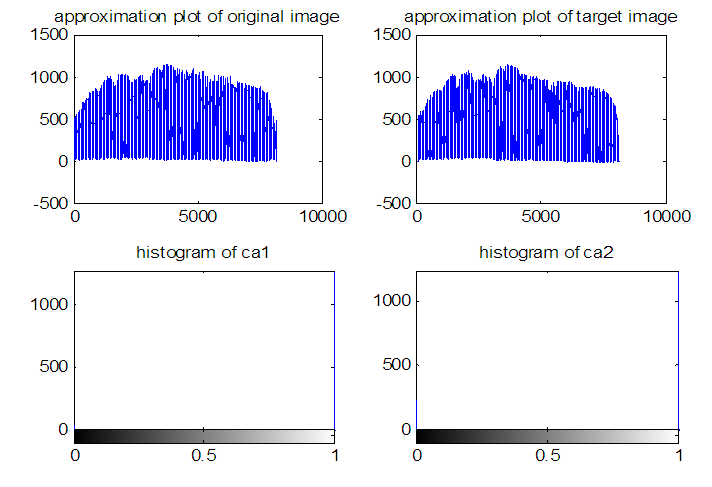 | Figure 12. Approximation and histogram of the image |
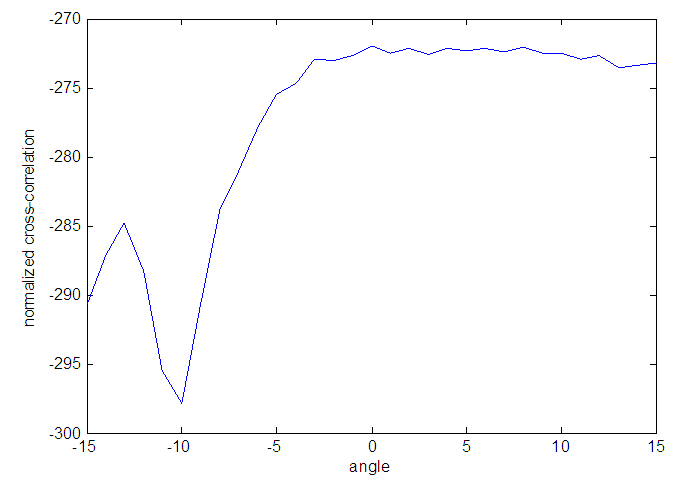 | Figure 13. Normalized cross-correlation Vs angle plot |
 | Figure 14. Final result |
Table 2. Time and root mean square record using the same image
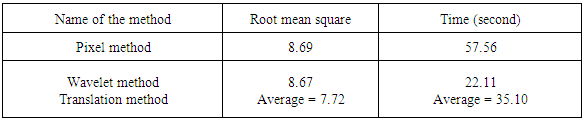 |
| |
|
In the case of translation registration the displaced image is shifted from its original position to another position by adding a certain value which is given randomly in the code and we get same result as other registration process. But in the translation registration process we have faced a problem the although it can detect the point of displacement the plot cannot show its original minimum point. We also have to use the extra code name ‘crop’ function to get the original image as a registered image. We see that in the above two cases where both the rotation and translation means displacement along the axis occurs the time needed by the wavelet method is very shorter than the pixel method. From all the experimented results we can make a conclusion that we actually can get back the original image from the rotated image that is the registered image. The ‘tic toc’ function let us know that the time we need is a little more than we have expected but it due to the simulation speed of the MATLAB software we have to wait for this time. We also find that when there is both the random rotation and the displacement along the x axis and along the y axis this system can detect the displacement. But when only the displacement along the axis occurs it cannot be detected. Because the original image is 512*512 in size but the displaced image is not as same as the original. That’s why we have to take a different process to do this. We have to make both the image of the same size otherwise it won’t work.
5. Conclusions
In this work image registration techniques are utilized in the pixel domain, wavelet domain, translation domain to register various images. These are normalized cross correlation (NCCR) based image registration. All these techniques are used and rough similarity transformation parameters were achieved. Comparison between results obtained from normalized root mean square distortion (NRMSD) and from the duration of processing using the ‘tic’ and ‘toc’ function. Applying different registration techniques we find that it gives the best results for normalized cross correlation (NCCR) and in translation domain calculation. Image registration is a vital problem in medical imaging. It has many potential applications in clinical diagnosis (Diagnosis of cardiac, retinal, pelvic, renal, abdomen, liver, tissue etc disorders) [7, 8]. It is a process of aligning two images into a common coordinate system thus aligning them in order to monitor subtle changes between the two. Registration algorithms compute transformations to set correspondence between the two images the purpose of this paper is to provide a comprehensive review of the existing literature available on Image registration methods. We believe that it will be a useful document for researchers longing to implement alternative Image registration methods for specific applications. We will make a toolbox that will automatically calculate the given image and give us the desired image. We will also develop our speed of processing speed that even a low processor computer can process all the data very fast. We will add some extra features in the toolbox to make it more users friendly and it will be able to compete with other image processing techniques. There will be a 3D version of this process and all the images can be analyzed in 3 dimension [9, 10].Sometimes it’s a time consuming matter to analyze the image displacement so we will find a good way to analyze it in a very short time. There is some kind of connection in between the code and the software because of which it takes time to analyze the image. We will find the most efficient way to analyze the image.
References
| [1] | Y.M. Zhu and S.M. Cochoff, "An object-oriented framework for medical image registration, fusion, and visualization," Computer Methods and Programs in Biomedicine, vol. 82, pp. 258 267, 2006. |
| [2] | X.Y. Wang, D.D. Feng, and H. Hong, "Novel elastic registration for 2D medical and gel protein images," APBC'03, vol. 19, pp. 223-226, 2003. |
| [3] | X. Wang and D.D. Feng, "Automatic hybrid registration for 2dimensional CT abdominal images," Third International Conference for Image and Graphics, Australia, pp. 208-211, December 2004. |
| [4] | D.G. Lowe, "Object recognition from local scale-invariant features," International Conference on Computer Vision, Corfu, Greece, pp. 1150 -1157, September 1999. |
| [5] | D.G. Lowe, "Distinctive image features from scale-invariant keypoints," International Journal of Computer Vision, vol. 60, no. 2, pp. 91-110, 2004. |
| [6] | E.I. Zacharaki and D. Shen, “ORBIT: A multiresolution framework for deformable registration of brain tumor images," IEEE Trans. on Medical Imaging, vol. 27, no. 8, pp. 1003-1017,August 2008. |
| [7] | S. Suri, P. Schwind, P. Reinartz, and J. Uhl, "Combining mutual information and scale invariant feature transform for fast and robust multisensor SAR image registration," Proc. of the 75 ASPRS Annual Conference, Batlimore, Maryland, USA, 2009. |
| [8] | J. P. Lewis, Fast Template Matching. Vision Interface, pp. 120-123, 1995. [9] S. Veeser, M.J. Dunn, and G.Z. Yang, "Multiresolution image registration for two-dimensional gel electrophoresis," Proteomics, vol. 1, pp. 865-870, 2001. |
| [9] | S. Gefen, O. Tretiak, and J. Nissanov, "Elastic 3-D alignment of rat brain histological images," IEEE Trans. on Medical Imaging, vol. 22, no. 11, pp. 1480-1489, November 2003. |
| [10] | J.P.W. Pluim, J.B.A. Maintz, and M.A. Viergever, "Mutualinformation-based registration of medical images: a survey," IEEE. |

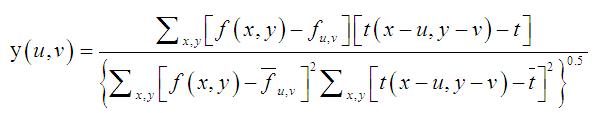 Where f is the image,
Where f is the image, 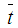 the mean of the template,
the mean of the template, 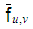 is the mean of f(x,y) in the region under the template.
is the mean of f(x,y) in the region under the template.











 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML



