| [1] | Samson Mil’shtein, P. Ersland, “Progress of quantum electronics and the future of wireless technologies,” Microelectronics Journal, vol. 39, issues 3-4, March–April 2008, pp. 669-673. |
| [2] | S. Mil’shtein, C. Liessner, “High Speed switch using pairs of pHEMTs with shifted gates,” Microelectronics Journal, vol. 36, issues 3-6, March-June 2005, pp. 316-318. |
| [3] | Christopher W. Liessner. 2005. “A high speed RF switch using shifted-gate pHEMTs,” University of Massachusetts, Lowell. |
| [4] | Michael Roberts, Lutfi Albasha, Wolfgang Bosch, Damian Gotch, James Mayock, Pallavi Sandhiya, Ian Bisby, “Highly Linear Low Voltage GaAs pHEMT MMIC Switches for Multimode Wireless Handset Applications,” , IEEE Radio and Wireless Conference, August 19-22, 2001, pp. 61-64. |
| [5] | Zeji Gu, Dave Johnson, Steven Belletete, Dave Fryklund, “Low Insertion Loss and High Linearity PHEMT SPDT and SP3T Switch ICs for WLAN 802.11a/b/g Applications,” IEEE Radio Frequency Integrated Circuits (RFIC) Symposium, Digest of Paper, June 6-8, 2004, pp. 505-508. |
| [6] | J. A. del Alamo, “The High Electron Mobility Transistor at 30: Impressive Accomplishments and Exciting Prospects,” International Conference on Compound Semiconductor Manufacturing Technology, May 16-19, 2011, pp. 17-22. |
| [7] | Jay Yang, Rick Cory, “Ultra-Miniature High Linearity SPDT Switch for WLAN Applications,” Microwave Product Digest, February 2010. |
| [8] | Kevin Walsh, “RF Switches Guide Signals in Smart Phones,” Microwaves & RF, September 2010, vol. 49, issue 9, p. 80. |
| [9] | Chang-Ho Lee, Bhaskar Banerjee, Joy Laskar, “Novel T/R Switch Architectures for MIMO Applications,” IEEE MTT-S International Microwave Symposium Digest, vol. 2, pp. 1137-1140. |
| [10] | Robert H. Caverly, “Distortion in Broad-Band Gallium Arsenide MESFET Control and Switch Circuits,” IEEE Transactions on Microwave Theory and Techniques, vol. 39, no. 4, pp. 713-717, 1991. |
| [11] | Kai Chang, Inder Bahl, Vishay Nair. 2002. “RF and Microwave Circuit and Component Design for Wireless Systems” Wiley, John & Sons, Incorporated, New York, p. 222. |
| [12] | C. –J. Wei, A. Klimashov, Y. Zhu, E. Lawrence, G. Tkachenko, “Large-Signal PHEMT Switch Model, Which Accurately Predicts Harmonics and Two-Tone Inter-Modulation Distortion,” IEEE MTT-S International Microwave Symposium Digest, June 12-17,2005. |
| [13] | Yu Zhu, Cejun Wei, George Nohra, Cindy Zhang, Oleksiv Klimashov, Hong Yin, Dylan Bartle, “Electromagnetic Only HEMT Model for Switch Design,” Asia Pacific Microwave Conference, December 7-10, 2009 , pp. 273-276. |
| [14] | Dong-Ming Lin, Chien-Chang Huang, Yi-Jen Chan, “A Symmetrical Model for Microwave Power AlGaAs/InGaAs pHEMTs for Switch Circuit Applications,” IEEE Transactions on Electron Devices, vol. 56, no. 11, pp. 2638-2643, 2009. |
| [15] | Ce-Jun Wei, Yu Zhu, Hong Yin, Olesky Klimashov, Dylan Bartle, “A Comprehensive PHEMT Core Model for Switch Applications,” IEEE MTT-S International Microwave Symposium Digest, June 5-10, 2011, pp. 1-4. |
| [16] | Ce-Jun Wei, Hong Yin, Olesky Klimashov, Yu Zhu, Dylan Bartle, “Multi-gate pHEMT Modeling for Switch Applications,” IEEE Compound Semiconductor Integrated Circuit Symposium, October 14-17, 2012, pp. 1-4. |
| [17] | Faramarz Kharabi, “Modeling of FET Switches,” IEEE Compound Semiconductor Integrated Circuit Symposium, October 14-17, 2012, pp. 1-4. |
| [18] | Ce-Jun Wei, Yu Zhu, Alex Klimashov, Hong Yin, Cindy Zhang, Dylan Bartle, “Distributed Switch FET Model that Predicts Better Insertion Loss and Harmonics,” European Microwave Integrated Circuits Conference, pp.238-241. |
| [19] | P. J. Rudge, R. E. Miles, M. B. Steer, and C. M. Snowden, “Investigation into Intermodulation Distortion in HEMTs Using a Quasi-2-D Physical Model,” IEEE Transactions on Microwave Theory and Techniques, vol. 49, no. 12, pp. 2315-2321, 2001. |
| [20] | P. R. Pantoja, M. J. Howes, J. R. Richardson, and C. M. Snowden, “A Large-Signal Physical MESFET Model for Computer-Aided Design and Its Applications,” IEEE Transactions on Microwave Theory and Techniques, vol. 37, no. 12, pp. 2039-2045, 1989. |
| [21] | R. J. Trew, “MESFET Models for Microwave Computer- Aided Design,” Microwave Journal, vol. 33, pp 115-130, May 1990. |
| [22] | R.B. Hallgren and P. H. Litzenberg, “TOM3 Capacitance Model: Linking Large- and Small-Signal MESFET Models in SPICE,” IEEE Transactions on Microwave Theory and Techniques, vol. 47, no. 5, pp. 556-561, 1999. |
| [23] | W. R. Curtice, “A MESFET Model for Use in the Design of GaAs Integrated Circuits,” IEEE Transactions on Microwave Theory and Techniques, vol. 28, no 5, pp. 448-456, 1980. |
| [24] | L. Angelov, N. Roreman, J. Stenarson, M. Garcia, and H. Zirath, “An Empirical Table-Based FET Model,” IEEE Transactions on Microwave Theory and Techniques, vol. 47, no. 12, pp. 2350-2357, 1999. |
| [25] | J. Gao, X. Li, H. Wang, and G. Boeck, “Empirical All region Current Based PHEMT DC Model,” SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference, 2003. Proceedings of the 2003, vol. 1, no. 9, pp. 99-101. |
| [26] | G. Qu, A. E. Parker, “Modeling HEMT intermodulation distortion characteristics,” Microelectronics Journal, vol. 31, issue 7, July 2000, pp. 493-496. |
| [27] | Ristesh Gupta, Sandeep Kumar Aggarwal, Mridula Gupta, R. S. Gupta, “Analytical non-linear charge control model for InAlAs/InGaAs/InAlAs double heterostructure high electron mobility transistor (DH-HEMT),” Solid-State Electronics, vol. 49, issue 2, February 2005, pp. 167-174. |
| [28] | Michael Wren, Thomas J. Brazil, “Enhanced Prediction of pHEMT Nonlinear Distortion Using a Novel Charge Conservative Model,” IEEE MTT-S International Microwave Symposium Digest, vol. 1, pp. 31-34, June 6-11, 2004. |
| [29] | Paul M. White, Wolfram C. Stiebler, Philip C. Balas, “Improved Modified Materka Model for Simulation of Pinch-Off Variation in PHEMT Devices,” European Microwave Integrated Circuits Conference, pp. 414-416, September 10-13, 2006. |
| [30] | Ritesh Gupta, Sandeep k. Aggarwhal, Mridula Gupta, R. S. Gupta, “An analytical model for discretized doped InAlAs/InGaAs heterojunction HEMT for higher cut-off frequency and reliability,” Microelectronics Journal, vol. 37, issue 9, September 2006, pp. 919-929. |
| [31] | B. Luo, Y. X. Guo, S. Y. Wong, L. C. Ong, “Modeling of 0.15μm InGaAs pHEMT up to 60 GHz,” IEEE International Workshop on Radio-Frequency Integration Technology, 2007, December 9-11, 2007, pp. 286-289. |
| [32] | Ce-Jun Wei, Yu Zhu, Hong Yin, Oleksiy Klimashov, Cindy Zhang, Tzung-Yin Lee, “Capacitance and RF-Conductance /Transconductance Look-up Table Based pHEMT Model,” Asia-Pacific Microwave Conference Proceedings, December 5-8, 2011, pp. 1246-1249. |
| [33] | A. Raffo, A Santtarelli, P.A. Traverso, M. Pagani, F. Palomba, F. Scappaviva, G. Vannini, F. Filicori, “Improvement of PHEMT Intermodulation Prediction Through the Accurate Modelling of Low-Frequency Dispersion Effects,” IEEE MTT-S International Microwave Symposium Digest, June 12-17, 2005. |
| [34] | Masaya Iwamoto, Jianjun Xu, Jason Horn, David E. Root, “III-V FET High Frequency Model with Drift and Depletion Charges,” IEEE MTT-S International Microwave Symposium Digest, June 5-10, 2011, pp. 1-4. |
| [35] | “European Telecommunications Standards Institute. Digital cellular telecommunications system (Phase 2+); radio transmission and reception (3GPP TS 45.005 version 5.9.0 Release 5),” ETSI, 2003b, Sophia Antipolis, France, Technical Specification ETSI tS 145 005 v5.9.0 (2003-2008). |
| [36] | “3GPP Technical Specification Group, Radio, Radio Access Network, Working Group 1, Spreading and Modulation (FDD),” April 1999, 3GPP Document TS S1.13 V2.00. |
| [37] | http://www.skyworksinc.com/products.aspx?CategoryID=629. |
| [38] | S. Mil’shtein and C. Liessner “Field Effect Transistor with Shifted Gate” Patent# 11,407,381 (2006). |
| [39] | S. Mil’shtein and J.Palma, C. Liessner “Field Effect Transistor with Independently Biased Gates” Patent # 11,406,838 (2006). |
| [40] | C. Liessner, J. Barrett, J. Palma, D. Gleason, and S. Mil’shtein, “Improving FET Switch Linearity”, Electron Devices, Vol. 54, Number 3, March 2007, pp. 391-397. |
| [41] | Andrew Dearn, Liam Devlin, Wing Yau, Owen Yu, “Design Trade-offs for High Linearity pHEMT Switches,” 53rd IEEE International Midwest Symposium on Circuits and Systems, August 1-4, 2010, pp. 942-945. |
| [42] | Michael D. Yore, Corey A. Nevers, Philippe Cortese, “High-Isolation Low-Loss SP7T pHEMT Switch Suitable for Antenna Switch Modules,” European Microwave Integrated Circuits Conference, September 27-28, 2010, pp. 69-72. |
| [43] | J. C. Pedro and N. B. Carvalho. 2003, “Intermodulation Distortion in Microwave and Wireless Circuits,” Artech House, London. |

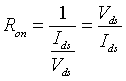
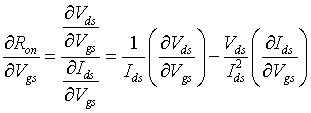
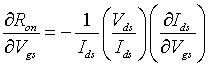
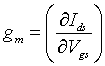
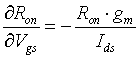

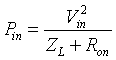

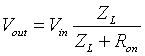
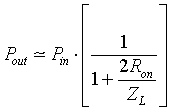

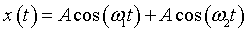
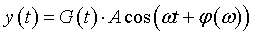
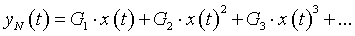
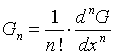
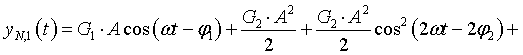
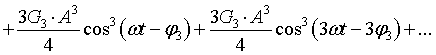
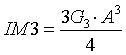
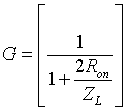
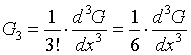
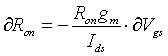
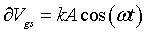
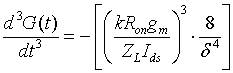
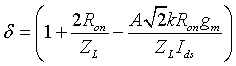
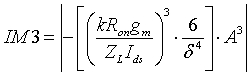
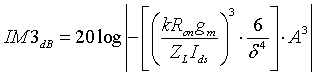
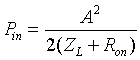

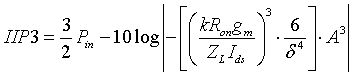
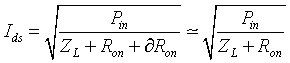
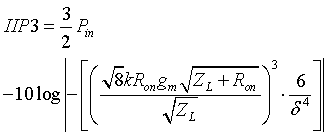
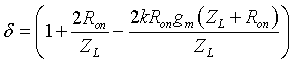



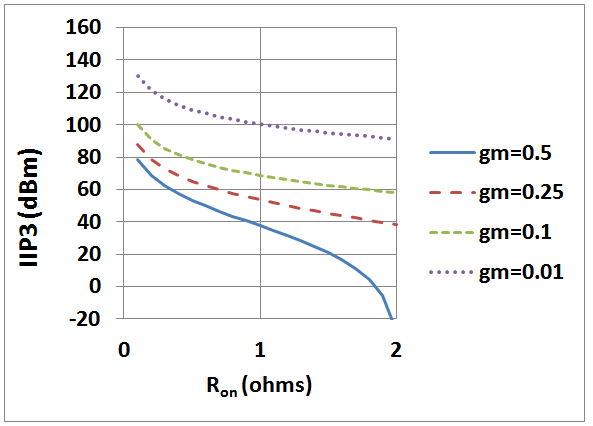
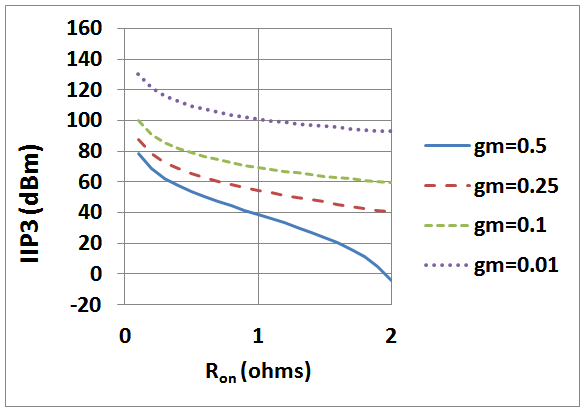
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML