Rubén Villafuerte D.1, Rubén A. Villafuerte S.2, Jesús Medina C.3, Edgar Mejia S.3
1Department of Electrical Engineering, Faculty of Engineering, Universidad Veracruzana, Ciudad Mendoza Ver, 94724, Mexico
2Department of electricalEngineering, Instituto Tecnológico de Orizaba, Orizaba, Ver, 94320, México
3Department of Mechanical Engineering, Faculty of Engineering, Universidad Veracruzana, Ciudad Mendoza Ver, 94724, Mexico
Correspondence to: Rubén Villafuerte D., Department of Electrical Engineering, Faculty of Engineering, Universidad Veracruzana, Ciudad Mendoza Ver, 94724, Mexico.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The power flow calculation in power networks generally carried out using iterative methods such as the Jacobi method, the Gauss-Seidel method, and the Newton-Raphson method. The authors present in this paper an investigation on the methods for solving nonlinear equations proposed by other authors, and are modified to solve nonlinear equations generated in the load flow study of a power system and is obtained efficient iterative method based on the three steps original formula of Newton-Raphson method and multi-step optimal algorithms for the solution of nonlinear equations.
Keywords:
Iterative Methods, Nonlinear Equations, Electrical Network, Power Flow, Multi-Step Algorithms
Cite this paper: Rubén Villafuerte D., Rubén A. Villafuerte S., Jesús Medina C., Edgar Mejia S., Multi-Step Methods Applied to Nonlinear Equations of Power Networks, Electrical and Electronic Engineering, Vol. 3 No. 5, 2013, pp. 128-132. doi: 10.5923/j.eee.20130305.02.
1. Introduction
In electrical engineering there are different types of studies to determine how they behave in different variables which are referred to as steady state and transient state. The electrical energy used in a city is manifested in electric generators are designed to generate and subsequently be sent to users. The electrical power transmitted to the cities receives the name of power flow, this is accomplished in what is known permanent state and involves the establishment of several nonlinear equations, which are generated from the application of the Kirchhoff's current law at each of the points or nodes of interest, which are defined by the analyst grids. The literature in electrical engineering[1,2] contains methods that have traditionally been used to solve the power flow problem, which is to calculate the voltages at each grid substation, knowing the demand and electric power generation in each of these.The Jacobi method: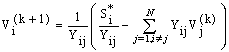 | (1) |
Fori=2, NIt's a simple formulation that iteratively calculates the voltage Vi in the current iteration and only requires the value of the other voltages in the previous iteration. 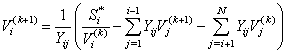 | (2) |
For i = 2, NWhich in order to accelerate the convergence requires voltage values of the previous iteration, and voltage values of the current iteration.The Newton-Raphson method: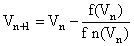 | (3) |
Matrix formulations of this method in which evaluates the jacobian matrix formed by the derivative of the function at each node generated according to voltages and angles, or in function of the rectangular components of voltages, are used to solve the nonlinear equations which involve the study of flow in electric power load. Based on that, there are several companies that have been developing commercial software for solving very efficient electric grids.In an electrical network with N nodes independent set an equation for node i, has the following form: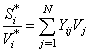 | (4) |
For i=2, NWhere: Si is the complex conjugate net power demanded at node i.Equation (4) can also be written as: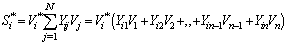 | (5) |
Or as a complex function, depending on all the voltages Vi.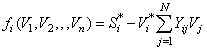 | (6) |
The formulas (4) and (6) are used to solve the nonlinear equations of a power grid with two, twenty, or more nodes.
2. Iterative Methods for Solving Nonlinear Equations
There are in the literature an important number of methods for the solution of nonlinear equations, among which we can mention the following[1]:Steffensen’s method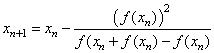 | (7) |
Secant method: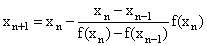 | (8) |
In electrical networks the Gauss-Seidel method is used to calculate the voltage Vi at each node by using equation [2,3]: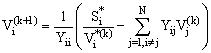 | (9) |
In the solution of a nonlinear equation, due to their stability and convergence the Newton-Raphson method [4] has been widely used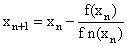 | (10) |
3. Multi-Step Iterative Methods for Solving Nonlinear Equations
Many multistep iterative methods for solving non-linear real equations have been proposed, among which are the following:Frozen slope method[4]: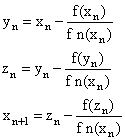 | (11) |
Weerakon and Fernando method [5]: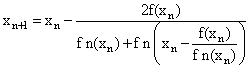 | (12) |
Kung-Traubmethod [6]: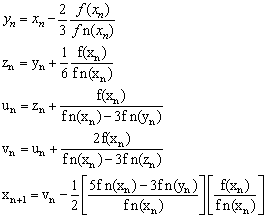 | (13) |
Cordero´s method [3]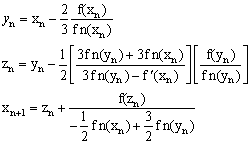 | (14) |
Liang F. algorithms[8] are fifth order in which the number of iterations is reduced significantly in solving nonlinear equations with real numbers.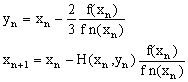 | (15) |
Where 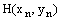 are as follows:
are as follows: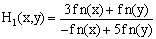 | (16) |
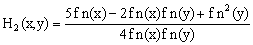 | (16a) |
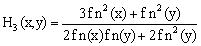 | (17) |
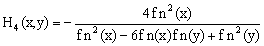 | (18) |
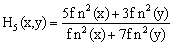 | (19) |
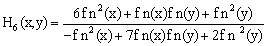 | (20) |
Jarratt’s method P. [7]: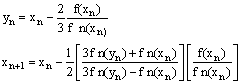 | (21) |
4. Multi-Step Methods for Solving Nonlinear Equations of Power Systems
Figure 1 shows a power system of four nodes, the values of the voltages at nodes 1, 2, 3, and 4, depends on the generated power and demand in each node or substation. The voltages of each node can obtain generating equation (6), and if desired using the method of Jacobi, Gauss-Seidel method, or a matrix formulation of the Newton-Raphson method[1].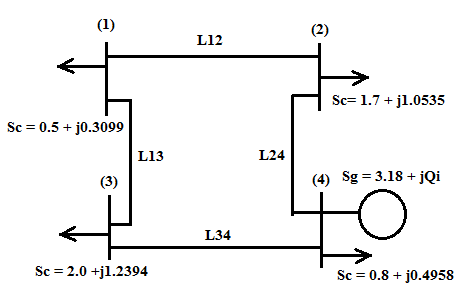 | Figure 1. System power of four nodes |
To calculate the voltage of this system, we can establish the following equations:For node two: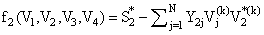 | (22) |
For node three: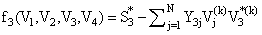 | (23) |
For node four: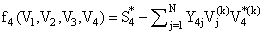 | (24) |
In addition, at the four nodes we have to calculate: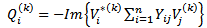 | (25) |
Yij system constants are calculated using the series impedance, parallel admittance of the transmission line, and are:Y21=-3.8156+j190781; Y31=-5.1696+j25.8478; Y41=0+j0Y22= 8.9852-j44.8360; Y32=0+j0; Y42= -5.1696+j25.8478Y23=0+j0; Y33=8.1933-j40.8638; Y43= -3.0237+j15.1185Y24= -5.1696+j25.8478; Y34= -3.0237+j15.1185;Y44= 8.1933-j40.8638Methods for nonlinear equations mentioned above are applied to solve equations with real numbers. The authors refer to their convergence characteristics, and have shown a favourable performance. However, the equations (22), (23), (24), and (25), are complex. All previous methods have presented convergence problems. Because it has been used the following methods of several steps: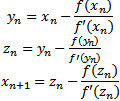 | (26) |
Because in Equation (26), the derivative is changing, is called variable slope method.A multistep method is formed with the original formula of Newton-Raphson, two terms of the formula of fifth order of Fang Liang, is as follows [8], Other authors have proposed methods without the second derivative [10,11].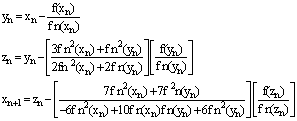 | (27) |
5. Results
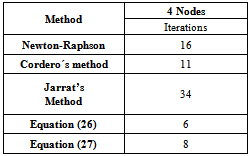
We investigate the performance of five methods that have been modified to determine the voltages for each node in the system shown in Figure 1. Table 1 lists all methods and iterations they need to achieve convergence.We developed a program for each equation in visual Fortran, because in this language is easy to work with complex numbers[12].Table 1. Iterations for a four-node system
 |
| |
|
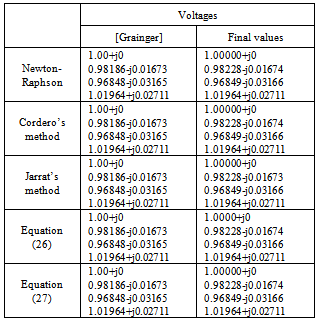
Table 2 shows the nodal voltages values calculated for each ofthe methods.The large electrical networks generally have a greatest number of nonlinear equations, and more restrictions. This makes the number of iterations increases, and causes slower convergence. The five previous methods have been used to solve the nonlinear equations of a network of nine nodes, eight nonlinear equations[9]. Figure 2 shows the network of nine nodes.Table 2. Final voltage values
 |
| |
|
The results of a program developed with equations (26) and (27) are shown in Table 3.Table 3. Values obtained with equations (26) and (27)
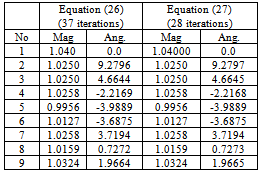 |
| |
|
Table 4 also shows the number of iterations of each method in a system of eight linear equations (9 nodes). Table 4 shows the iterations that used the Newton-Raphson method, Cordero´s method and Jarrat´s method in the system of Figure 2Table 4. Iterations for a system of nine nodes
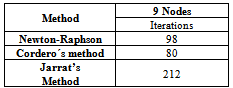 |
| |
|
The solution of nonlinear equations with the classical formula of Newton-Raphson method is simple, although the number of iterations to achieve convergence increases when the equations are numerous. Using high-order formulas such as the Cordero, and Gouping Liang Fang He, and adapting, accelerates the convergence in solving systems of nonlinear equations on a grid, as shown in Table 3.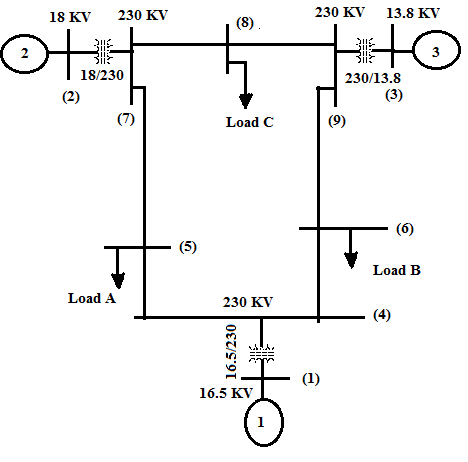 | Figure 2. Nine-nodes test system [9] |
6. Conclusions
Based on the original form of the Newton-Raphson method and multistep methods, and establishing a multi-step algorithm for solving nonlinear equations generated in the steady-state study of electrical networks. The original equations[3, 8] were taken as the basis for creating a multi-step method that would achieve convergence when there are power systems with voltage controlled nodes. It was considered the establishment of a function at each network node that depends on several variables, instead of creating a system of equations where the matrix manipulation is usually very elaborate. Power systems so far are of moderate size and almost didactic purposes; however, let you know in a fast steady-state behaviour of an electrical network. Its application is certainly possible to other fields of engineering.We are simulating the behaviour of methods third and fifth order, which have preliminary results that will be reported in other work later.
References
| [1] | J. J. Grainger and W. D. Stevenson Jr, “Análisis de sistemas de potencia”, McGraw-Hill, 1996. |
| [2] | Jizhong Zhu, “Optimization of Power System Operation”, Wiley/IEEE, 2009. |
| [3] | Cordero A., Hueso, J. L., Martínez, E. Terregosa J. R., “A ModifiedNewton-Jarrat’s composition”, NumericalAlgorithm, 55 (2010), 87-99. |
| [4] | Hueso J. l.,Martínez E., Terregrosa, J. R., “Third order iterative Methods free from second derivative for nonlinear systems”, Applied mathematics and Computation, 211 (2009), 190-197. |
| [5] | Weerakon S., Fernando T. G. I, “A variant of Newton’s method with accelerated third-order convergence”, Applied Mathematics Letters, 13(8) (2000)87-93 |
| [6] | Kung H. T., Traub J. F., “Optimal order of one-point and multipoint iteration”, Journal ACM, 21 (1974) 643-651. |
| [7] | Jarratt P., “Some fourth order multipoint methods for solving equations”, Mathematics and Computations, 20 (1966) 434-437 |
| [8] | Liang F. and Gouping He, “Some modifications of Newton’s method with Higher-order convergence for solving nonlinear equations”, Journal of Computational and Applied Mathematics 228(2008) 296-303. |
| [9] | P. M. Anderson & A. A. Fouad, “Power System Control and stability”, 2nd edition IEEE Press Power Engineering Series, Wiley-Interscience, 2003. |
| [10] | Muhammad Aslam Noor, “Fourth-Order Iterative Method Free from Second Derivative for Solving Nonlinear Equations”, Applied Mathematical Sciences, Vol. 6, 2012, no. 93, 4617 – 4625. |
| [11] | Gustavo Fernandez Torres and Juan Vazquez Aquino, “Three New Optimal Fourth-Order Iterative Methods to Solve Nonlinear Equations”, Advances in Numerical Analysis, Volume 2013, (2013) Article ID 957496, 8 pages. |
| [12] | Visual Fortran 90, User Guide. |

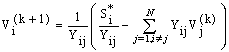
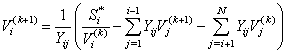
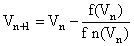
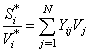
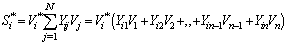
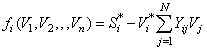
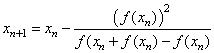
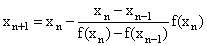
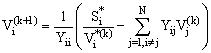
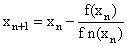
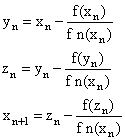
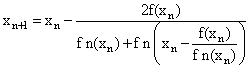
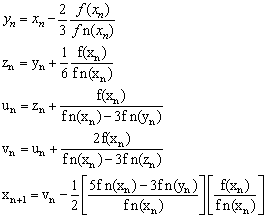
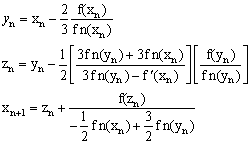
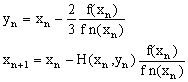
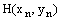 are as follows:
are as follows: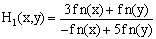
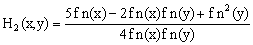
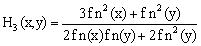
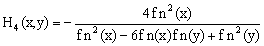
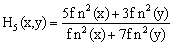
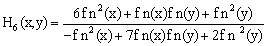
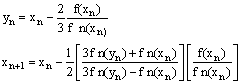

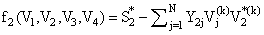
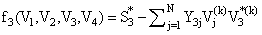
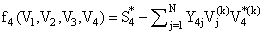
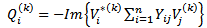
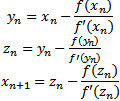
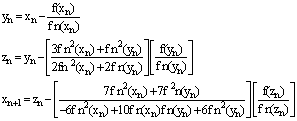

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


